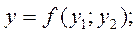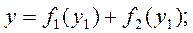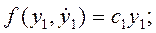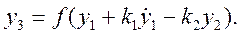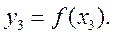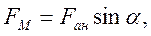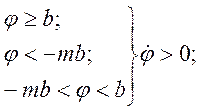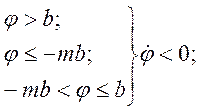Простая математическая модель петли гистерезиса для нелинейных материалов Текст научной статьи по специальности « Физика»
Аннотация научной статьи по физике, автор научной работы — Лукичев А. А., Ильина В. В.
Статья посвящена разработке простой и легко интерпретируемой математической модели петли гистерезиса для нелинейных материалов. Получены аналитические выражения, позволяющие моделировать гистерезис при различных режимах колебаний и с различными функциями насыщения. Определены критические точки петли и найдена их зависимость от свойств материала. Показана применимость полученной модели к описанию гистерезисных зависимостей реальных материалов.
Похожие темы научных работ по физике , автор научной работы — Лукичев А. А., Ильина В. В.
SIMPLE MATHEMATICAL MODEL OF HISTERESIS LOOP FOR NONLINEAR MATERIALS
The paper is devoted to development of simple and easily interpreted mathematical model of a hysteresis loop for nonlinear materials. The analytical expressions are received, allowing to model a hysteresis at various regimes of vibrations and with various functions of saturation. Critical points of a loop are defined and their dependence on properties of material is found. Applicability of the developed model to the description hysteresis dependences of real materials is shown.
Текст научной работы на тему «Простая математическая модель петли гистерезиса для нелинейных материалов»
УДК 53.072; 537.226.4; 548.537.611
ПРОСТАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПЕТЛИ ГИСТЕРЕЗИСА ДЛЯ НЕЛИНЕЙНЫХ МАТЕРИАЛОВ
© 2011 А.А. Лукичев, В.В. Ильина
Институт геологии и природопользования ДВО РАН, г. Благовещенск
Поступила в редакцию 10.03.2011
Статья посвящена разработке простой и легко интерпретируемой математической модели петли гистерезиса для нелинейных материалов. Получены аналитические выражения, позволяющие моделировать гистерезис при различных режимах колебаний и с различными функциями насыщения. Определены критические точки петли и найдена их зависимость от свойств материала. Показана применимость полученной модели к описанию гистерезисных зависимостей реальных материалов. Ключевые слова: петля гистерезиса, математическое моделирование, нелинейные диэлектрики, ферромагнетики.
Явление гистерезиса хорошо известно в физике, технике, экономике и других отраслях науки. В физике гистерезисные зависимости встречаются у различных материалов с нелинейным откликом на внешнее воздействие, в частности у ферромагнетиков и нелинейных диэлектриков.
В настоящее время имеется достаточно много математических моделей гистерезисных зависимостей 3. Имеющиеся модели гистерезиса построены на решении нелинейных дифференциальных уравнений, либо на введении нелинейных гистерезисных членов в линейные уравнения. Подобным образом построены модели Прайсаха, Джилеса-Атертона, Хаузера и другие. Использование нелинейных уравнений приводит к значительному усложнению модели из-за того, что трудно получить универсальное решение и интерпретировать результаты. В случае линейного уравнения сложно найти достаточно простую добавку, которая не приводила бы к значительным математическим трудностям и позволяла бы воспроизвести параметры петли. Если гистерезисный член прост, как, например, функция Прайсаха и подобные ей [3], то здесь требуется задание параметров петли, т.е. такой подход позволяет получить только полуэмпирические модели. Общим недостатком указанных моделей является то, что они не позволяют получить простое аналитическое выражение, позволяющее моделировать петлю гистерезиса.
Поскольку практический метод получения петли Сойера-Тауэра [4] прост, то можно пред-Лукичёв Александр Александрович, кандидат физико-математических наук, старший научный сотрудник лаборатории конструкционной керамики. E-mail: lukichevaa@mail.ru.
Ильина Виктория Владимировна, кандидат физико-математических наук, младший научный сотрудник лаборатории конструкционной керамики. E-mail: nastja-5051974@mail.ru
положить, что математическая модель гистерезис-ной петли тоже должна быть не сложной. Из способа Сойера-Тауэра также следует, что, в отличие от перечисленных выше, модель должна быть макроскопической. При разработке модели мы будем исходить из достаточно очевидного факта, согласно которому причиной появления петли гистерезиса является инерционность вещества, т.е. имеется отставанием по фазе между внешним воздействием и откликом материала.
Очевидно, что закономерности образования петли гистерезиса в нелинейных диэлектриках и ферромагнетиках одинаковы. Для описания магнитных материалов используется соотношение
Б(^а) = /и(ю,Н)/и0 Н(0 , (1)
для диэлектриков используется аналогичное выражение:
Р(г,ю) = а(с, Е) ■ Е(г), (2)
здесь ) — магнитная индукция, ¡л0 — магнитная постоянная, /л(о,И)- магнитная проницаемость, Н(Ь)- напряженность магнитного поля, Р(Ь)- вектор поляризации, а(о,Е) — поляризуемость, Е(Ь)-напряженность электрического поля.
Далее будем рассматривать некий абстрактный материал с функцией отклика вида (1), (2): У^,с) = Л(с, X) X^), (3)
— внешнее гармоническое воздействие, Л(а,Х) -коэффициент, зависящий от частоты изменения внешнего поля сои амплитуды внешнего воздействия Х(Ь), или спектральная функция. С математической точки зрения равенство (3) представляет собой параметрическую зависимость, где t является параметром. Как следует из (3), форма петли гистерезиса определяется видом функции Л(а),Х).
Сначала рассмотрим линейный гистерезис. В этом случае, коэффициент Л(а,Х) не зависит от
амплитуды внешнего воздействия и зависит только от частоты.
Известно, что форма спектров, как магнитной индукции, так и поляризации, во многих случаях близки к спектральной функции линейного осциллятора. Для резонансного режима колебаний [5] это функция Лоренца:
для заторможенного режима- укороченная спектральная функция:
ю)+2ip п/2 угловой коэффициент меняет знак, и петли с фазой п-убудут зеркальным отражением петель с фазой р.
Учтем частотную зависимость амплитуды колебаний. Построим графики для линейного гистерезиса, используя спектральную функцию Лоренца (5), в резонансном режиме колебаний (Ь=(,1ф(), рис. 3а, и для заторможенного режима (Ь=5ю(), рис. 3б. В резонансном режиме зависимость формы петли от частоты и фазы рез-
Рис. 1. а — зависимость от частоты модуля спектральной функции Лоренца (5); б — Зависимость от частоты фазы функции Лоренца. Цифрами на графиках обозначена величина относительного затухания в/а. Пунктирная линия — граница между резонансным и заторможенным режимами колебаний. При затухании выше 3 графики функция Лоренца полностью совпадает с функцией Дебая (6)
Рис. 2. Графики для линейного гистерезиса, функция (9). Цифрами на графиках обозначена величина фазового сдвига
ко выражена вблизи резонансной частоты. При приближении к резонансу амплитуда, ширина петли и угловой коэффициент быстро возрастают. При тзю имеется широкая симметричная
вертикальная петля большой амплитуды. На боковых спадах резонансной кривой петли имеют малую амплитуду и ширину. Из рисунка видно, что боковые петли несимметричны относитель-
но частоты резонанса, это следствие асимметрии спектральной функции. При малых затуханиях (Ь д) эти различия будут невелики, при больших затуханиях (Ь>0,1а>0), возникает значительная асимметрия. Также следует учитывать, что а>реззаметно отличается от сод, и срез =п/2) будет меньше амплитуды наклонной петли соответствующей с=юрез (рис. 3а).
Если У0>>Х0, что обычно выполняется для нелинейных материалов, то можно считать, что при малых значениях отклика У@,а) боковая образующая петли — прямая, и ее наклон совпадает с наклоном главной оси и определяется выражением (10).
В отличие от резонансного режима, для заторможенных колебаний (Ь>юд) и амплитуда, и фаза меняются плавно в широком диапазоне частот. Как видно из рис. 3б, с ростом частоты петля плавно уширяется, её амплитуда снижается. При нулевой фазе (с0) эллипс вырождается в прямую угловым коэффициентом к=У/Хд, это значение углового коэффициента максимальное. Симметричная петля (д>=п/2) имеет очень маленькую амплитуду.
Как следует из рис. 1б, для резонансного режима колебаний фаза меняется достаточно резко от 0 до -п, в узкой области частот вблизи резонанса. При больших затуханиях (заторможенный режим) фаза будет ненулевой практически во всем интервале рабочих частот, диапазон изменения фазы от 0 до -п/2. Отсюда следует, что
Рис. 3. а — линейный гистерезис для резонансного режима колебаний, спектральная функция (5), в/а =0,1 б — линейный гистерезис для заторможенного режима колебаний, спектральная функция (5), в/а0=5 Цифрами на графиках обозначена величина фазового сдвига Петля с ^=84,2о на рисунке а соответствует максимуму модуля спектральной функции (5)
в резонансном режиме петля имеет заметную ширину только в области резонанса (р^трез), в заторможенном режиме ширина петли будет ненулевой практически во всём диапазоне частот, где имеется заметная амплитуда колебаний. Для заторможенных колебаний угловой коэффициент петли может быть только положительным, в резонансном режиме он может менять знак.
Очевидно, что линейный гистерезис во многом подобен фигурам Лиссажу.
Рассмотрим характерные точки петли и найдем их связь с параметрами входного воздействия и отклика материала. Из рисунков видно, что ширина и наклон петли существенно зависят от фазового сдвига и отношения У0/Х. Найдём ширину петли по точкам пересечения оси ОХ, из равенства: = У0(ю)sin(юt + р) = 0.
Соответственно, ширина петли будет равна 2АХ. Таким образом, ширина петли определяется только величиной входного воздействия и фазой отклика.
Для описания нелинейного гистерезиса нам необходимо найти спектральную функцию, которая бы зависела от частоты и фазы, и от амплитуды. Зависимость спектральной функции от амплитуды отклика наблюдается только для нелинейных осцилляторов [7]. Но, чтобы не усложнять задачу, мы будем считать колебания линейными. Поскольку спектральные функции линейного осциллятора не зависит от амплитуды, попробуем сконструировать нужную функцию, используя спектральные функции (5), (6) и имеющиеся функции насыщения.
В настоящее время известна только одна теоретически обоснованная функция насыщения — это функция Ланжевена, которая используется как в теории магнетизма так и в физике диэлектриков [8]:
Для диэлектриков величина a = p0E / Ш, где р0 — элементарный дипольный момент частиц, участвующих в процессе поляризации, к -постоянная Больцмана, Т — температура. В теории магнетизма a = m0Н ^ /Ш , где т0 — элементарный магнитный момент, Ие- эффективное поле [8]. График функции Ланжевена показан на рис. 4.
В теории Ланжевена рассматривается магнитное поле, действующее на отдельно взятый домен внутри материала. Но внутри материала действует эффективное поле, которое является
суперпозицией внешнего и внутреннего (реактивного) полей [8].
^ Fef = Fr + Ft, г (13)
где Fr — реактивное поле материала, Fi — внешнее поле. Реактивное поле появляется как отклик материала на внешнее воздействие и, следовательно, зависит от частоты. В магнитных материалах это молекулярное поле Вейсса, в диэлектриках — локальное поле Лоренца. Для нелинейных материалов, как правило, Fr >> Fi, следовательно Fef « Fr. Очевидно, что реактивное поле пропорционально отклику материала на внешнее воздействие вида (9), т.е.
Fr = F0|Л( Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Рис. 4. Зависимость функции Ланжевена Ь(а) (12) и экспоненциальной функции насыщения Б(¥) (16) от величины реактивного поля
Рис. 5. Гистерезисная зависимость функции Ланжевена от величины внешнего воздействия.
Цифрами на графиках обозначена величина фазового сдвига
функций не зависит от частоты и равна 1. Для того, чтобы учесть спектральную зависимость амплитуды необходимо ввести множитель в виде модуля спектральной функции. Таким образом, сейчас мы можем записать обобщённую спектральную функцию, зависящую от амплитуды, частоты и фазы:
где Бо -обобщённая функция насыщения, У -амплитудный множитель. Поскольку амплитуда нелинейного гистерезиса будет заведомо меньше амплитуды линейного гистерезиса, здесь введён амплитудный множитель У, равный отношению амплитуд нелинейного и линейного процессов. Очевидно, что произведение У|А(й>)| равно насыщенному значению функции (17). Частотная зависимость реактивного поля определяет форму петли, спектральный множитель влияет на её амплитуду. Построим петлю гистерезиса с помощью равенства (17). В качестве функции насыщения используем функцию Ланжевена. Графики функции (17) показаны на рис. 5.
Как видно из рисунка, зависимость амплитуды, угла наклона и ширины петли от частоты и фазы такая же, как и для линейного гистерезиса. Петли с большой амплитудой имеют закруглённые концы. Это свойство функции Ланжевена, которая описывает процесс достаточно плав-
ного насыщения. Для материалов с более резким насыщением, предпочтительнее использовать экспоненциальную функцию (16).
Найдём характерные точки нелинейной петли. При малых амплитудах функцию насыщения можно считать линейной, следовательно, ширина петли определяется так же, как и для линейного гистерезиса (11), соответственно коэрцитивная сила равна полуширине петли: Xc = X0 sin р . Найдём значение функции (17) при X(t)=0, для магнитных материалов эта величина называется остаточной намагниченностью. Из условия: rat=0 находим значение реактивного поля для этой точки: Fr0 = F0|^(®)|sin( р), и далее находим соответ-вующее ему значение функции насыщения
Определим наклон боковых образующих нелинейной петли. Разложим функцию Ланжевена в ряд на линейном участке в окрестности нуля L(a))=a/3 [8], откуда, используя (14) и (15) получаем:
Y (t’ ®) = YT Fef = YT FoHHsin(® t + р). (19)
Далее, по аналогии с (10), находим угловой коэффициент:
X0 3kT sin(^ /2 — р)
Если также разложить в ряд экспоненциальную функцию насыщения (16), то полученный угловой коэффициент будет совпадать с (20) с точностью до постоянных множителей. Из равенства (20) следует, что по наклону линейной петли гистерезиса можно определить амплитуду напряженности внутреннего поля ¥.
Для того, чтобы показать применимость разработанной выше модели для описания гистере-зисных зависимостей реальных материалов авторами были сняты гистерезисные зависимости для феррита НМ2000 и трансформаторного железа. Феррит имеет выраженную резонансную зависимость магнитной проницаемости от частоты с резонансной частотой /И/400 кГц. В линейном режиме гистерезисные зависимости для феррита точно повторяли приведённые на рис. 3а. В нелинейном режиме петли имели форму, близкую к приведённым на рис. 5. Для трансформаторного железа, имеющего АЧХ дебаевского вида, как линейные, так и нелинейные петли в основном подчинялись общим закономерностям, показанным на рис. 3б. Отсюда следует, что полученная модель позволяет описать поведение реальных материалов и найти связь формы петли и свойств материала.
1. М.А. Красносельский, А.В. Покровский. Системы с гистерезисом. М.: Наука, 1983. 275 с.
2. Hauser H., Fulmek P.L., Grossinger R. Hysteresis modeling and measurement for two-dimensional particle assembles//J. of magnetism and magnetic materials, Vol. 242-245, 2002. Р. 1067-1069.
3. Bottauscio O., Chiampi M., Chiarabaglio D., Repetto M. Preisach-type hysteresis models in magnetic field computation.//Physica B, Vol. 275, 2000.- p.p.24-39.
4. Барфут Дж., Тейлор Дж. Полярные диэлектрики и
их применение. М.: Мир, 1981. 526 с.
5. Ильина В.В., Лукичев А.А. Различные режимы вынужденных колебаний линейного осциллятора с затуханием и исследование соответствующих спектральных функций //Известия Самарского научного центра РАН. 2008. Т. 10. №3. C. 782-790.
6. Поплавко Ю.М. Физика диэлектриков. Киев, Вища школа, 1980. 400 с.
7. Кузнецов А.П., Кузнецов С.П., Рыскин Н.М. Нелинейные колебания. М.: Физматлит, 2002. 292 с.
8. Тамм И.Е. Основы теории электричества. Москва, Наука, 1976. 616 с.
SIMPLE MATHEMATICAL MODEL OF HISTERESIS LOOP FOR NONLINEAR MATERIALS
© 2011 A.A. Lukichev, V.V. Iljina
Institute of Geology and Nature Management of RAS, Blagoveschensk
The paper is devoted to development of simple and easily interpreted mathematical model of a hysteresis loop for nonlinear materials. The analytical expressions are received, allowing to model a hysteresis at various regimes of vibrations and with various functions of saturation. Critical points of a loop are defined and their dependence on properties of material is found. Applicability of the developed model to the description hysteresis dependences of real materials is shown. Keywords: histeresis loop, math simulation, nonlinear dielectrics, ferromagnetic,.
О дифференциальных уравнениях систем гистерезисного типа тема автореферата и диссертации по математике, 01.01.02 ВАК РФ
На правах рукописи
О дифференциальных уравнениях систем гистерезисного типа
Специальность 01.01.02 — дифференциальные уравнения, динамические системы и оптимальное управление
диссертации на соискание ученой степени кандидата физико-математических паук
Работа выполнена на кафедре функционального анализа и операторных уравнений Воронежского государственного университета
Научный руководитель: доктор физико-математических наук,
профессор Садовский Борис Николаевич
Официальные оппоненты: доктор физико-математических наук,
профессор Перов Анатолий Иванович
доктор физико-математических наук, профессор Семенов Михаил Евгеньевич
Ведущая организация: Институт проблем передачи информации
им. A.A. Харкевнча РАН
Защита состоится 21 декабря 2010 г. в 15 час. 10 мин. на заседании диссертационного совета Д 212.038.22 при Воронежском государственном университете но адресу: 394006, г. Воронеж, Университетская пл., 1.
С диссертацией можно ознакомиться в научной библиотеке Воронежского государственного университета.
Автореферат разослан ноября 2010 г.
диссертационного совета Д 212. 038. 22 доктор физико-математических наук, профессор
Общая характеристика работы
Актуальность темы. Системы с гистерезисом активно изучаются в связи с различными задачами физики, техники, теории управления. Основы математической теории систем с гистерезисом заложены в монографии М.А. Красносельского и A.B. Покровского «Системы с гистерезисом». В последовавшей серии работ различных авторов при изучении систем гистерезисного типа использовались явные н полуявные описания гнстерсзнсных элементов по Красносельскому — Покровскому, а также в последнее время локально явное описание Прядко — Садовского. В диссертации изучена возможность описания гнстсрезисных элементов и систем с гистерезисом с помощью обыкновенных дифференциальных уравнений, содержащих большой параметр. Такой подход позволяет применять для численного и качественного анализа систем с гистерезисом программы и методы, разработанные для обыкновенных дифференциальных уравнений.
Целью работы являются разработка гладких описаний гнстерсзнсных элементов, сравнение новых описаний с известными дискретными, явными и полуявными, изучение примеров систем гнстсрезисных типов с использованием гладких моделей.
Методика исследований. В диссертации использовались методы теории функций и нелинейного функционального анализа; идеи и методы теории дифференциальных уравнений.
Научная новизна. Перечисленные ниже основные результаты диссертации являются новыми.
1. Разработаны описания реле с гистерезисом, упора, люфта и системы с диодной нелинейностью в виде систем обыкновенных дифференциальных уравнений с большим параметром.
2. Доказаны теоремы о близости поведений систем гистерезисного типа при использовании классических моделей, с одной стороны, и разработанных в диссертации гладких описаний — с другой.
3. Проведено исследование ряда конкретных систем гистерезисного типа с использованием гладких описаний.
В частности, введено и исследовано понятие выходной функции реле на всей оси; исследованы системы автоматического управления с одним, двумя реле; изучено поведение выходной функции бесконечного множества реле; рассмотрены примеры численного анализа оператора упора и люфта, изучена система с диодной нелинейностью в четырехугольнике на плоскости; доказана теорема о существовании и усиленной орбитальной устойчивости замкнутой траектории; проведены численные эксперименты по нахождению замкнутой траектории.
Теоретическая и практическая ценность. Полученные результаты имеют как теоретическую, так и практическую направленность; они могут быть использованы при исследовании конкретных систем гистерезисного типа и приближенном решении связанных с ними задач.
Апробация работы. Результаты, представленные в диссертации, могут найти применение в исследованиях по теории систем с гистерезисом, проводимых в научных коллективах Института проблем управления РАН, Института проблем передачи информации РАН, а также Воронежского, Нижегородского, Ростовского, Саратовского, Челябинского и Ярославского государственных университетов.
Публикации. Основные результаты диссертации опубликованы в работах [1] — [7]. В совместных публикациях [5], [6] соавтору принадлежит постановка задач.
Структура диссертации. Диссертация состоит из введения, 5 глав и списка литературы, включающего 55 источников. Общий объем диссертации — 99 страниц.
Краткое содержание работы
Во введении обоснована актуальность темы диссертации, дан краткий обзор исследований по ее тематике н приведена общая информация о предлагаемых в работе математических описаниях таких элементов
и систем, как реле с гистерезисом, упор, люфт и система с диодной нелинейностью.
Реле рассматривается как преобразователь с произвольным непрерывным входом x(t) и выходом y(t), имеющим два возможных значения 0 и 1, причем при x(t) ß — только 1. О скачком меняется на 1 при достижении входным сигналом значения ß, 1 па 0 — при достижении а. При этом a,ß (а а.
В монографин М.А. Красносельского и A.B. Покровского «Системы с гистерезисом» дапо следующее явное оннсание такого реле, в котором начальное состояние (хо, Уо) 6 /?):
О, если x(t) ßV 3(ti)[x(ti) = ßh V(r e
При таком описании выходная функция меняет свое значение точно в моменты достижения входной функции пороговых значений, т.е. выходная функция непрерывна справа.
Следуя статье И.Н. Прядко и Б.Н. Садовского «О локально явных моделях некоторых негладких систем», выходной сигнал можно задать локально явным уравнением:
y(t), если а 0. В дальнейшем, если (хо,Уо) лежит в области допустимых состояний реле в виде локально явного уравнения (2), то мы обозначим В,1а(а,(3,х)(уо) решение этого уравнения, удовлетворяющее начальному условию у(Ьо) = уо. Утверждение о существовании и единственности такого решения доказано в той же статье.
Нелинейности люфт и упор широко используются в различных разделах физики, механики, теории управления и др. Одномерный упор, соответствующий отрезку [0,1] — это преобразователь, который монотонно возрастающему входу х(Ь) (£ > £о) и начальному состоянию щ ё [0,1] сопоставляет выходной сигнал и(£), который возрастает с той же скоростью, что и вход х<<), до тех пор, пока и(Ь) не становится равным верхнему ограничению 1; после этого при дальнейшем возрастании входного сигнала, выход и(Ь) равняется единице, т.е. и(£) = тт<1,:г(£) — х(Ь0) + «(£о)>— Для убывающего входа > ¿о) и начального состояния щ е [0,1] выход и(£) со скоростью входа убывает до достижения нижнего ограничения 0; после этого при дальнейшем убывании входного сигнала, выход и(£) не меняется, т.е. и(<) = тах<0, — + 0)>.
Одномерный люфт, соответствующий отрезку [0,1] — это преобразователь, который монотонно возрастающему непрерывному входу х(Ь) и начальному состоянию зд € + 1] сопоставляет
выход г;( о, покаа;(£) + 1 > г>о, и х<£) +1 в дальнейшем, т.е. = гшп<г>о, х<Ь) + 1>. Такие описания упора и люфта очевидным образом распространяются на кусочно монотонные непрерывные входы.
В монографии М.А. Красносельского и А.В. Покровского «Системы с гистерезисом» дано следующее описание упора и люфта. Кусочно-гладкая входная функция > Ц) преобразуется в выходные упора функцию
Ф = < гпах<0, х>, если 0 можно задать локально явными уравнениями:
В параграфах 2.3 — 2.5 сформулирована и доказана теорема о близости. Рассматриваются следующие две системы:
и = Щ,и,у), Щ = Ко решение и(£) системы (10) удовлетворяет неравенству:
Доказательство этой теоремы проводится с помощью леммы о зависимости решений от начальных данных и параметра (в п. 2.5.1) и следующих утверждений (в и. 2.5.2 — 2.5.5): утверждения об оценке времени
срабатывания гладкого реле; утверждения о близости поверхностей уровня; утверждения об оценке промежутка между выходами на пороговые значения и утверждения об оценке близости.
В параграфе 2.6 изучается частный случай, в котором рассматриваемые системы (9) н (10) являются скалярными. Тогда при некоторых условиях на функцию / указанную оценку для С в теореме о близости можно улучшить, а параметр К > 0 в (8) можно выбирать произвольно.
В третьей главе рассматриваются примеры анализа некоторых систем с релейным управлением. В параграфе 3.1 изучается система с одним реле на плоскости:
ущ+ и|. При этом доказывается критерий периодичности решений: для того, чтобы начиная с некоторого момента, решение системы (11) было периодическим, необходимо и достаточно, чтобы £ 6 О,
/0М) г > 0, причём существует конечный предел ¡(х, 1) при х —> ^^ + 0. Тогда для любого Хо €Е К\ каждое решение системы (12), начиная
с некоторого момента, является периодическим вправо и любые два решения этой системы, начиная с некоторого момента, совпадают с точностью до сдвига по времени.
В этом параграфе доказаны утверждения о существовании и единственности периодического выхода с любым наперед заданным средним значением из некоторого отрезка, однозначно определяемого входной функцией.
В четвертой главе для гистерезисных преобразователей упора и люфта предложены гладкие описания в виде обыкновенных дифференциальных уравнений с большим параметром. Описания упора и люфта, построенные в этой главе, отличаются от описаний (3) и (4) тем, что с помощью сглаженной входной функции £(£) для непрерывной входной функции а:(£)(£ € [¿сь?1]) (см- параграф 4.1) они определяются
сразу для любых непрерывных функций, а не только кусочно гладких входов. Именно, гладкие выходные функции упора u(t) и люфта v(t), соответствующие непрерывному входу x(t) п (большому) параметру К, зададим уравнениями:
u = i + I 0 на [to, Т] будет верна следующая оценка: \u(t)-
Для люфта утверждение формулируется следующим образом: пусть ip(t), v(t)
решения, соответственно, уравнения (4) и (14), удовлетворяющие начальным условиям:
Тогда для любого К > 0 па [fo, Т] будет верна следующая оценка:
В параграфе 4.5 на основе гладкого описания упора н люфта приводятся эксперименты численного анализа, в которых получены приближенные решения систем (3) и (4) с непрерывной входной функцией.
В последней пятой главе изучается гладкое описание системы с диодной нелинейностью. Для системы обыкновенных дифференциальных уравнений с разрывной правой частью вида (7) построена и изучена близкая к ней система с непрерывной правой частью и большим параметром К. Такое гладкое описание определяется следующим уравнением (см. параграф 5.1):
Здесь у = Р(у,Я) — проекция у на — непустое замкнутое выпуклое множество в М»; для I 6 [¿о, ¿о+Т] и х £ £о + Т] верна следующая оценка:
В частном случае (в параграфе 5.3) по сравнению с (15) введено и другое гладкое описание — более эффективное, не использующее оператора проектирования. В двумерном пространстве К2 рассмотрим множество (3 как пересечение двух полупространств (¿1 и О н х* е intQ
(см. п. 5.6.1). В пункте 5.6.2 доказана теорема, в которой найдено достаточное условие на параметр е > 0 для того, чтобы все условия обобщенной теоремы были выполнены.
В параграфе 5.7 на основе (16) определено гладкое описание для примера из предыдущего параграфа. При этом доказана теорема об оценке близости между решениями классического и гладкого описания. Кроме того, приводятся некоторые эксперименты численного анализа и для одного конкретного получена оценка близости между соответствующими решениями.
Публикации автора по теме диссертации
[1] Нгуен Тхи Хиен. Анализ автоколебании в системе с двумя реле / Нгуен Тхи Хиен // Труды математического факультета. — Воронеж: ВорГУ, 2006. — Вып. 10 (новая серия). — С. 112-118.
[2] Нгуен Тхи Хиен. Анализ автоколебаний в системе с двумя реле / Нгуен Тхи Хиен // Воронежская зимняя математическая школа С.Г. Крейна: тез. докл, Воронеж, 2006 г. — Воронеж: ВорГУ, 2006. — С. 69.
[3] Нгуен Тхи Хиен. Гладкие модели упора и люфта / Нгуен Тхи Хиен // Вестник ВГУ. Серия: Физика. Математика. — 2009. — № 2. — С. 92-95.
[4] Нгуен Тхи Хиен. Гладкие модели упора и люфта / Нгуен Тхи Хиен // Воронежская зимняя математическая школа С.Г. Крейна: тез. докл, Воронеж, 2010 г. — Воронеж: ВорГУ, 2010. — С. 108-109.
[5] Нгуен Тхи Хиен. Гладкая модель реле с гистерезисом / Нгуен Тхи Хиен, Б.Н. Садовский // Воронежская зимняя математическая школа С.Г. Крейна: тез. докл, Воронеж, 2010 г. — Воронеж: ВорГУ, 2010, с. 109-110.
[6] Нгуен Тхн Хиен. Гладкая модель реле с гистерезисом / Нгуен Тхи Хиен, Б.Н. Садовский // Автом. и телемех. — 2010. — № 11. — С. 100-111.
[7] Нгуен Тхи Хиен. О точности гладкой модели системы с диодной нелинейностью / Нгуен Тхи Хиен // Вестник ВГУ. Серия: Физика. Математика. — 2010. — № 2. — С. 240-243.
Работы [6], [7] соответствуют списку ВАК.
Подл, в печ. 12.11.2010. Формат 60*84 V,6. Усл. печ. л. 0,93. Тираж 80 экз. Заказ 1435.
Отпечатано с готового оригинал-макета в типографии Издательско-полиграфического центра Воронежского государственного университета. 394000, Воронеж, ул. Пушкинская, 3 Тел. 204-133
1 Предварительные результаты для изучения систем с релейным управлением
1.1 Утверждение об практической эквивалентности описания реле в виде локально явного уравнения явному описанию по Красносельскому — Покровскому.
1.2 Свойства реле Я\
1.2.2 Вольтерровость — причинность.
1.2.3 Полугрупповое свойство.
1.3 Определение Я*
1.4 Свойства Н^оо
1.4.2 Вольтерровость — причинность.
1.4.3 Полугрупповое свойство.
1.5 Утверждение о периодических входах и выходах.
2 Гладкое описание реле с гистерезисом
2.1 Постановка задачи.
2.2 Теорема о степени несовпадения выходов гладкого и локально явного описания.
2.3 Формулировка теоремы о близости.
2.4 Оценки констант.’.
2.5 Доказательство теоремы о близости.
2.5.1 Лемма о зависимости решений от начальных данных и параметра.
2.5.2 Утверждение об оценке времени срабатывания гладкого реле.
2.5.3 Утверждение о близости поверхностей уровня
2.5.4 Утверждение об оценке промежутка между выходами на пороговые значения.
2.5.5 Утверждение об оценке близости.
2.6 Частный случай
2.6.1 Оценка констант С в частном случае
3 Примеры анализа некоторых систем с релейным управлением
3.1 Система с одним реле на плоскости
3.1.1 Постановка задачи.
3.1.2 Теорема (критерий периодичности решений)
3.1.3 Эксперименты численного анализа.
3.1.4 Оценка близости к решениям системы с локально явным описанием реле.
3.2 Система с двумя реле.
3.2.1 Постановка задачи.
3.2.2 Утверждение о существовании периодического решения
3.3 Бесконечная система реле
3.3.1 Лемма о двоичной системе
3.3.2 Утверждение о существовании периодического выхода
3.3.3 Утверждение о существовании и единственности периодического выхода.
4 Гладкое описание упора и люфта
4.1 Постановка задачи.
4.2 Утверждение об оценке близости выходов упора с гладким входом.
4.3 Утверждение об оценке близости выходов у пора с непрерывным входом.
4.4 Утверждение об оценке близости для выхода люфта с непрерывным входом.
4.5 Эксперименты численного анализа и оценки близости
5 Гладкое описание системы с диодной нелинейностью
5.1 Постановка задачи.
5.2 Теорема о точности гладкого описания системы с диодной нелинейностью.
5.3 Частный случай
5.5 Обобщенная теорема о существовании и единственности предельного цикла (см.[22]).
5.6 Пример применения обобщенной теоремы
5.6.1 Постановка задачи.
5.6.2 Теорема о замкнутой траектории.
5.7 Оценка близости и эксперименты численного анализа
5.7.1 Теорема об оценке близости.
5.7.2 Эксперименты численного анализа.
Появление математических описаний гистерезисных явлений обусловливалось достаточно богатым набором прикладных задач (прежде всего в теории автоматического регулирования), в которых носители гистерезиса нельзя рассматривать изолированно, поскольку они являлись частью некоторой более сложной системы. Создание математической теории гистерезиса относится к 60-м годам XX века, когда в Воронежском государственном университете начал работать семинар под руководством М. А. Красносельского, посвященный «гистерезисной» тематике. В связи с семинаром было подготовлено и опубликовано несколько работ (см. [14] — [18], [28] и [2]). Позднее, в 1983 году появилась монография [19], в которой различные гистерезисные явления получили формальное описание в рамках теории систем: гистерезисные преобразователи трактовались как операторы, зависящие от своего начального состояния кь,к от параметра, определённые на достаточно богатом функциональном пространстве (например, пространстве непрерывных функций), действующие в некоторое функциональное пространство. Различным вопросам, связанным с гистерезисными нелинейностями, посвящены многие сотни статей и монографий. Информацию о подходах к изучению гистерезисных явлений, а также обширную библиографию можно найти в [47], [48], [3], [4], [24], [12], [5], [13], [36], [37], [29] — [31] и [1].
По Я.З. Цыпкину уравнение гистерезисного элемента в общем случае определяется не функцией от входа х, а оператором, определенным на входах х, и может быть представлено в виде
Эта запись показывает, что выходная величина y(t) в момент t определяется значением входной величины x(t) не только в момент i, но и его значениями во все предыдущие моменты времени и, кроме того, y(t) зависит от некоторого параметра ст. Описания нелинейных элементов при наличии гистерезиса в общем случае можно найти в работах В.А. Якубовича [45], [46]. В цикле работ Я.З. Цыпкина (см. [40] — [43]) изучены различные аспекты теории релейных автоматических систем. Релейный элемент, отвечающий приведенному выше феноменологическому описанию, Я.З. Цыпкин называет элементом с положительным гистерезисом и без зоны нечувствительности (см. [44], с. 74). Если обозначим через ° — Ух £ <ОД>значение выходного сигнала после последнего момента ¿1 переключения реле, то уравнение такого элемента можно представить в следующем виде (приведем его в несколько измененной эквивалентной форме): y(t) = Ф(ж;2/1) =
1, если х > ß или ß > x(s) > а при у\ = 1;
0, если х ¿о), удовлетворяющие условию x(to) = Жо- Допустимому входу х(t) отвечает выход y(t) (t > to), который определяется соотношениями: г
О, если х(г) (ЗУ З^г^х^г) — ¡ЗА \/(т Е г])[ж(т) > а]], т/о? если ж(г) € (а, (3) при всех т Е [¿о?£]
Нетрудно видеть, что при таком описании выходная функция меняет свое значение точно в моменты достижения входной функции пороговых значений, т.е. выходная функция непрерывна справа.
Следуя [29], в соответствии с приведенным феноменологическим описанием выходной сигнал можно записать локально явным уравнением: ей) = (3, (2) если а 0.
Заметим, что для описания реле в виде локально явного уравнения (2) областью £1(а,/3) допустимых состояний реле с пороговыми значениями а и (3 является множество точек (х, у) плоскости, лежащих на двух полупрямых: у — 0 при х а. В дальнейшем, если (хо,Уо) лежит в этой области, то мы обозначим Щ (ос, /3,х)(уо) решение уравнения (2), удовлетворяющее начальному условию у(Ьо) = т/о- Утверждение о существовании и единственности такого решения доказано в [29].
В [30] показано, что при локально явном описании (2) реле обладает основными свойствами, отмеченными в [19], например, свойством монотонности по входам и монотонности по пороговым значениям. Кроме этого, доказана непрерывная зависимость выхода от входа при условии, что непрерывная входная функция в точках локального максимума не принимает значение ß, а в точках локального минимума — а. В локально явном уравнении (2) предполагается непрерывность выходной функции слева, что существенно связано со спецификой локально явных уравнений; практически описания (1) и (2) эквивалентны.
Нелинейности люфт и упор широко используются в различных разделах физики, механики, теории управления и др. (см., например, [11], [3], [10] и [19]). Одномерный упор, соответствующий отрезку [0,1] — это преобразователь, который монотонно возрастающему входу x
Одномерный люфт, соответствующий отрезку [0,1] — это преобразователь, который монотонно возрастающему непрерывному входу x
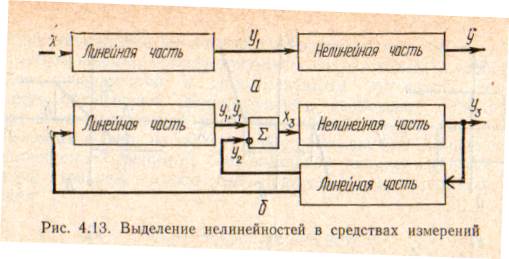
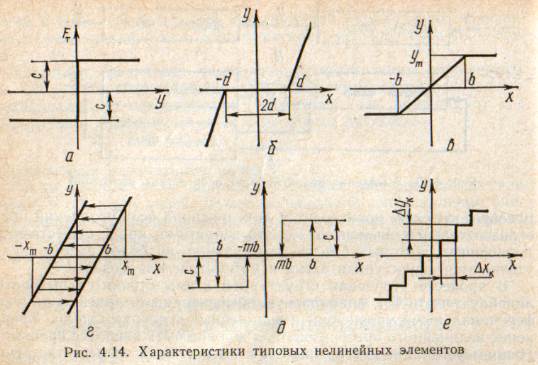
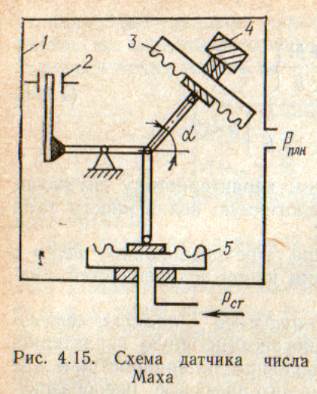
В монографии М.А. Красносельского и A.B. Покровского [19] дано следующее описание упора и люфта. Кусочно-гладкая входная функция x(t)(t > to) преобразуется в выходные упора функцию (p Ф — \ шах<0, £>, если = 0; min<0, £>, если • ip и х ь-> ф при фиксированных начальных значениях выходов удовлетворяют в норме пространства С условию Липшица с константами, соответственно, 1 и 2. Поэтому определения этих операторов распространяются по непрерывности на любые непрерывные входы. Кроме этого, доказано, что оператор люфта обладает свойствами детерминированности, статичности, управляемости, виброкоректности (с. 18) и самым важным свойством монотонности — люфт монотонен в том смысле, что увеличение (уменьшение) входного сигнала влечет увеличение (уменьшение) и выходного сигнала (с. 22). В силу связи между упором и люфтом (с. 111) получим, что преобразователь упора также обладает аналогичными свойствами. В [30] даются математические описания упора и люфта в виде локально явных уравнений. Для монотонных входов x(t) выходные сигналы упора u(t) и люфта v(t) при малых dt > 0 можно задать локально явными уравнениями: х(Ь + ей) — х <Ь) -4- если £ (0,1), ь(г + (И) = х(1 + - + если = и v(t + dt) = 0, и Список источников диссертации и автореферата по математике, кандидата физико-математических наук, Нгуен Тхи Хиен, Воронеж 1. Appell J. On the stability of some relay-type regulation system / J. Appell, 1.N. Pryadko, B.N. Sadovsky // Z. Angew. Math. Mech. 88. -2008. — № 10. — P. 808-816. 2. Владимиров A.A. Покровский A.B. Векторные гистерезисные нелинейности типа Мизеса Треска / A.A. Владимиров и др.] // ДАН СССР. — 1981. — Т. 257, № 3. — С. 506-509. 3. Воронов A.A. Основы теории автоматического управления / A.A. Воронов. М.: Энергия, 1980. — 312 с. 4. Гильман Т.С. Вынужденные колебания систем с простейшими ги-стерезисными нелинейностями / Т.С. Гильман, A.B. Покровский // ДАН СССР. 1982. — Т. 262, № 3. С. 437-450. 5. Golubev G. On the second order minimax estimation in partial linear models / G. Golubev, W. Hardie // Math. Methods of Stat. -2000. -V. 2. P. 160-175. 6. Данилов JI. В. Ряды Вольтерры-Пикара в теории нелинейных электрических цепей / JI.B. Данилов. М.: Радио и связь, 1987. — 224 с. 7. Данилов JI.B. Теория нелинейных электрических цепей / Л.В. Данилов, П.Н. Матханов, Е.С. Филиппов. Л.: Энергоатомиздат, 1990. — 256 с. 8. Дезоер Ч.А. Основы теории цепей / Ч.А. Дезоер, Э.С. Ку. М.: Связь, 1976. — 286 с. 9. Дробченко Е.Ю. Об устойчивости положения равновесия двумерной системы дифференциальных уравнений с фазовыми ограничителями / Е.Ю. Дробченко, Р.В. Нестеренко, Б.Н. Садовский // Вестник ВГУ. Серия: Физика. Математика. 2001. — № 1. С. 95-96. 10. Дюво Г. Неравенства в механике и физике / Г. Дюво, Ж.Л. Лионе. М.: Наука, 1980. — 384 с. 11. Емельянов C.B. Теория систем с переменной структурой / C.B. Емельянов. М.: Наука, 1970. — 592 с. 12. Зубов C.B. Устойчивость периодических решений в системах с гистерезисом / C.B. Зубов // Нелинейный анализ и его приложения: тез. докл. междунар. конгр, Москва, 1-5 сент. 1998 г. М., 1998. — С. 293-307. 13. Красносельский A.M. О континуумах циклов в системах с гистерезисом / A.M. Красносельский, Д.И. Рачинский // Доклады РАН. -2001. Т. 378, № 3. — С. 314-319. 14. Красносельский М.А. Оператор-гистерант / М.А. Красносельский и др.] // ДАН СССР. 1970. — № 1. — С. 29-33. 15. Красносельский М.А. Системы гистеронов / М.А. Красносельский, A.B. Покровский // ДАН СССР. 1971. — Т. 200, № 4, — С. 733-736. 16. Красносельский М.А. Периодические колебания в системах с релейными нелинейностями / М.А. Красносельский, A.B. Покровский // ДАН СССР. 1974. — Т. 216, № 4. — С. 733-736. 17. Красносельский М.А. Моделирование преобрзователей с гистерезисом континуальными системами реле / М.А. Красносельский, A.B. Покровский // ДАН СССР. 1976. — Т. 227, № 3. — С. 547-550. 18. Красносельский М.А. Правильные решения интегральных уравнений с разрывной нелинейностью / М.А. Красносельский, A.B. Покровский // ДАН СССР. 1976. — Т. 226, № 3. — С. 506-509. 19. Красносельский М.А. Системы с гистерерисом / М.А. Красносельский, A.B. Покровский. М.: Наука, 1983. — 272 с. 20. Лобанова O.A. О движении точки в ограниченном фазовом пространстве / O.A. Лобанова // Сборник статей аспирантов и студентов математического факультета ВГУ. Воронеж: ВорГУ, 1999. — С. 88-92. 21. Лобанова O.A. О существовании предельного цикла у линейной системы с ограничением / O.A. Лобанова // Вестник ВГУ. Серия: Физика. Математика. 2001. — № 1. — С. 108-110. 22. Лобанова O.A. О двумерных динамических системах с ограничением /O.A. Лобанова, Б.Н. Садовский // Дифференциальные уравнения.- 2007. Том. 43, № 4. — С. 449-456. 23. Матханов П. Н. Основы анализа электрических цепей. Нелинейныецепи / П. Н. Матханов. М.: Высшая школа, 1986. — 352 с.t 24. Mayergoyz I.D. Mathematical Models of Hysteresis / I.D. Mayergoyz. -New York: Springer, 1991. 207 p. 25. Нестеренко P.B. О вынужденных колебаниях в двумерном конусе / Р.В. Нестеренко, Б.Н. Садовский // Автом. и телемех. 2002. — № 2. — С. 14-21. 26. Петрова Л.П. К математической теории электрических цепей с диодными преобразователями тока / Л.П. Петрова, Б.Н. Садовский. -Воронеж: ВорГУ, 1982. 27 с. 27. Прядко И.Н. О локально явных моделях некоторых негладких систем / И.Н. Прядко, Б.Н. Садовский // Автом. и телемех. 2004. -№ 10. — С. 40-50. 28. Прядко И.Н. О локально явных уравнениях /И.Н. Прядко // Диссертация канд. физ.-мат. наук. Воронеж, 2006. — 115 с. 29. Pryadko I.N. On locally explicit equations and systems with switching / I.N. Pryadko, B.N. Sadovsky // Func. Diff. Equat. 2006. — T. 13, № 3-4. — P. 571-584. 30. Садовский Б.Н. Системы с диодными нелинейностями и максимальные монотонные операторы / Б.Н. Садовский. В кн.: VIII школа по теории операторов в функциональных пространствах, 2 часть. 1 Рига, 1983. 31. Садовский Б.Н. К математической теории цепей с тиристорами / Б.Н. Садовский, М.П. Соболевская // Сб. научных трудов Динамика неоднородных систем. Материалы семинара. М.: ВНИИСИ, 1984. — С. 178-182. 32. Садовский Б.Н. О двумерных динамических системах с ограничением / Б.Н. Садовский, O.A. Лобанова // Современные проблемы функционального анализа и дифференциальных уравнений: тез. докл. конф, 30 июня-4 июля, Воронеж, 2003 г. Воронеж, 2003. — С. 170-171. 33. Семенов М.Е. Математическое моделирование динамических систем с гистерезисными явлениями / М.Е. Семенов // Диссертация д-ра физ.-мат. наук. Воронеж, 2003. — 192 с. 34. Синицкий Л.А. Методы аналитической механики в теории электрических цепей / Л.А. Синицкий. Львов : Вища школа, 1978. — 138 с. 35. Теоретические основы электоротехники. Том I. Основы теории линейных цепей / Под редакцией Ионкина П.А. М.: Высшая школа, 1976. — 544 с. 36. Цыпкин Я.З. Частотные характеристики релейных следящих систем / Я.З. Цыпкин // Автом. и телемех. 1959. -Т. 20, № 12. — С. 16031610. 37. Цыпкин Я.З. Влияние случайных помех на периодический режим в релейных автоматических системах /Я.З. Цыпкин // Доклады АН СССР. -1961. Т. 139, № 3. — С. 570-573. 38. Цыпкин Я.З. Об устойчивости релейных автоматических систем «в большом»/ Я.З. Цыпкин // Известия АН СССР ОТН «Техника кибернетика». 1963. — № 3. С. 121-135. 39. Цыпкин Я.З. частотный метод анализа автоколебаний и вынужденных колебаний в релейных системах автоматического регулирования / Я.З. Цыпкин // под ред. Солодовникова «машиностроение». 1969. — Книга 3, ч. 2. — С. 101-104. 40. Цыпкин Я.З. Релейные автоматические системы /Я.З. Цыпкин. -М.: Наука, 1974. 575 с. 41. Якубович В.А. Частотные условия абсолютной устойчивости регулируемых систем с гистерезисным нелинейностями / В.А. Якубович // ДАН СССР. 1963. — Т. 149, № 2. — С. 288-291. 42. Якубович В.А. Метод матричных неравенств в теории устойчивости нелинейных регулируемых систем. III. Абсолютная устойчивость систем с гистерезистными нелинейностями / В.А. Якубович // Автом. и телемех. 1965. — Т. 26, № 5. — С. 753-763. 43. Якубович В.А. Частотные условия абсолютной устойчивости систем управления с несколькими нелинейными или линейными нестационарными блоками / В.А. Якубович // Автом. и телемех. 1967. -Т.23, №6. — С. 5-30. 44. Нгуен Тхи Хиен. Анализ автоколебаний в системе с двумя реле / Нгуен Тхи Хиен // Труды математического факультета. Воронеж: ВорГУ, 2006. — Вып. 10 (новая серия). — С. 112-118. 45. Нгуен Тхи Хиен. Анализ автоколебаний в системе с двумя реле / Нгуен Тхи Хиен // Воронежская зимняя математическая школа С.Г. Крейна: тез. докл, Воронеж, 2006 г. Воронеж: ВорГУ, 2006. — С. 69. 46. Нгуен Тхи Хиен. Гладкие модели упора и люфта / Нгуен Тхи Хиен // Вестник ВГУ. Серия: Физика. Математика. 2009. — № 2. — С. 92-95. 47. Нгуен Тхи Хиен. Гладкие модели упора и люфта / Нгуен Тхи Хиен // Воронежская зимняя математическая школа С.Г. Крейна: тез. докл, Воронеж, 2010 г. Воронеж: ВорГУ, 2010. — С. 108-109. 48. Нгуен Тхи Хиен. Гладкая модель реле с гистерезисом / Нгуен Тхи Хиен, Б.Н. Садовский // Воронежская зимняя математическая школа С.Г. Крейна: тез. докл, Воронеж, 2010 г. Воронеж: ВорГУ, 2010, с. 109-110. 49. Нгуен Тхи Хиен. Гладкая модель реле с гистерезисом / Нгуен Тхи Хиен, Б.Н. Садовский // Автом. и телемех. 2010. — № 11. — С. 100-111. 50. Нгуен Тхи Хиен. О точности гладкой модели системы с диодной нелинейностью / Нгуен Тхи Хиен // Вестник ВГУ. Серия: Физика. Математика. 2010. — № 2. — С. 240-243. Большинство СИ в общем случае описываются нелинейными уравнениями. Предположение о малых отклонениях измеряемой величины или использование, например, только линейной части характеристик преобразователей, в ряде случаев позволяет проводить их исследование как линейных, состоящих из линейных преобразовательных элементов. Однако при значительных изменениях измеряемой величины и более детальном изучении процессов, происходящих в измерительных цепях, необходимо строже учитывать явления, считавшиеся второстепенными и влекущими за собой появление существенных нелинейностей в статических и динамических характеристиках. Так, например, в преобразователях, содержащих механические элементы, зачастую не учитываются такие принципиально нелинейные явления, как сухое трение и влияние зазоров (люфтов), ограничений и упоров. Это может вызвать значительные погрешности и даже принципиальные ошибки при расисте и проектировании СИ. К нелинейным СИ относятся такие, которые содержат хотя бы один преобразователь, описываемый нелинейным уравнением. К нелинейным преобразователям в общем случае могут быть отнесены преобразователи, имеющие зависимости между входом и выходом: релейного типа; с кусочно-линейной характеристикой; с криволинейной характеристикой любого очертания; в виде уравнений, которые содержат произведение переменных или их производных и другие комбинации; нелинейные импульсные; логические, описываемые кусочно-линейными дифференциальными уравнениями. В общем случае при составлении математической модели нелинейных СИ придерживаются следующей последовательности: как и для линейных СИ на основании выявленных преобразований составляется структурная схема, а затем — математические модели преобразователей; производится линеаризация всех уравнений преобразовательных элементов, где это допустимо, кроме существенно нелинейных, которых бывает, как правило, не более одного-двух; уточняются структурная схема и математическая модель. В процессе уточнения структурной схемы стремятся выделить линейную часть СИ, описываемую обыкновенными линейными дифференциальными уравнения, и нелинейные преобразователи. Уравнение нелинейного преобразователя должно быть наиболее простым. Например, иногда удается выделить нелинейный элемент так, чтобы зависимость между выходной и входной величинами была непосредственной (рис. 4.13, а). Однако в некоторых случаях это сделать не удается и приходится исследовать более сложные зависимости: При этом если под знак нелинейной функции входит какая-либо линейная комбинация разных переменных, то целесообразно ее обозначить одной переменной, например (рис. 4.13,6) можно привести уравнение нелинейного элемента к простому виду: После преобразования и уточнения структурной схемы составляется одно или система дифференциальных уравнений линейной части средства измерений, например где А (р), В (р) — операторные многочлены. Причем в это уравнение должны быть включены и соотношения типа (4.99), получаемые при выделении нелинейностей. Эти уравнения или система совместно с уравнениями нелинейностей и являются основой для дальнейших исследований нелинейного СИ. Нелинейные уравнения СИ, например, с произведением переменных или их производных, криволинейными характеристиками и т. д., то есть не содержащие разрывов, резких изломов и др., могут быть получены с использованием обычных методов: уравнений Лагранжа, законов физики, принципа возможных перемещений и закона сохранения энергии. Поэтому рассмотрим лишь СИ с преобразователями, имеющими существенные нелинейности. При этом считаем, что, согласно структурному методу, эти преобразователи выделены и для линейной части составлена математическая модель на основании методов, описанных в настоящей главе. Проанализируем наиболее распространенные характеристики существенно нелинейных элементов: сухое, или кулоновское, трение; нечувствительность; ограничение; люфт; гистерезис; скачкообразное изменение величин; наличие упоров. Характеристики этих элементов при определенных допущениях могут быть достаточно хорошо представлены кусочно-линейными кривыми, которые называют типовыми статическими характеристиками. а) Нелинейности типа сухого трения (рис. 4.14, а), как правило, присущи элементам, содержащим трущиеся поверхности: подвижные части показывающих приборов, кинематические пары электромагнитных, емкостных и других преобразователей. При этом в таких элементах имеется, по крайней мере, три типа сил сопротивления, объединяемых термином «трение»: вязкое трение; трение покоя; кулоновское трение. При составлении динамических уравнений чаще всего учитывается вязкое трение, пропорциональное относительной скорости трущихся поверхностей и способствующее затуханию движения, то есть обладающее демпфирующим свойством. Трение покоя имеет место только при равенстве нулю относительной скорости. Кулоновское трение не зависит от скорости движения и обладает постоянной силой трения где у — относительная скорость поверхностей; с — постоянная величина. Если скорость у = 0, сила трения б) Нелинейность типа зоны нечувствительности (рис. 4.14, б) имеет место в ИП, нечувствительных к малым входным сигналам, например в индуктивных, емкостных, потенциометрических, тахогенераторах и др. Эта нелинейность может быть описана зависимостью где d — постоянная величина, определяющая ширину зоны чувствительности по отношению ко входному сигналу x; k — коэффициент преобразования. в) Нелинейность типа «насыщение» (рис. 4.14, в), или «ограничение», присуща множеству ИП, других механизмов и устройств и является следствием, например ограничения по мощности в усилительно- преобразовательных элементах, исполнительных устройствах, параметрических преобразователях и т. д. В данном случае преобразователь может рассматриваться как линейный в некотором диапазоне изменения входного сигнала, но при достижении сигналом определенного значения преобразователь становится нечувствительным к его дальнейшему изменению. Математическое описание нелинейности типа «насыщение»: где b — величина, определяющая значение входного сигнала, при котором наступает насыщение в преобразователе; ут — максимально возможное значение выходного сигнала. г) Нелинейность типа «зазор» (рис. 4.14, г) имеет место почти во всех механических соединениях. Зазор, или люфт, характеризуется величиной перемещения одного из сопряженных элементов соединения, не вызывающего перемещения другого, ведомого элемента. Математическая модель нелинейности имеет вид где 2b — ширина петли гистерезисного вида; хт — амплитуда входного сигнала. Как видно из уравнений (4.103), характеристика относится к классу многозначных, поскольку каждому значению входного сигнала х может соответствовать множество значений выходного сигнала у. Следует заметить, что некоторые ИП, имеющие нелинейности типа сухого трения, описываются нелинейностью в виде зазора. Это бывает, когда преобразователи содержат сравнительно легкие подвижные части и влиянием массы можно пренебречь. д) Нелинейность типа «трехпозиционное реле» (рис. 4.14, д) имеет место при использовании в измерительных пенях релейных или коммутационных элементов, гидравлических или пневматических клапанов, фрикционных муфт и т. д. Эта нелинейность имеет неоднозначную характеристику с высшим и низшим уровнями выходной величины [с; —с], зоной нечувствительности шириной 2b и петлей гистерезиса шириной (b — mb) «трехпозиционное реле с гистерезисом». При этом коэффициент т принимает значение в интервале [—1; 1]. В идеальном случае, когда скачкообразное изменение выходного сигнала с нулевого на высший или низший уровни и наоборот происходит при одном и том же значении входного сигнала, то есть m = 1, получим характеристику трехпозиционного реле без гистерезиса. Математическая модель в виде однозначной характеристики с разрывом в данном случае будет С учетом неоднозначности характеристики в интервале изменения входного сигнала [—b + тb; b — тb] математическая модель нелинейности типа «трехпозиционное реле» с гистерезисом выражается зависимостью Нетрудно убедиться, что, если положить т = 0, получим характеристику двухпозиционного реле с петлей гистерезиса, имеющего математическую модель Для случая, когда b = 0, получим характеристику двухпозиционного реле без гистерезиса, аналогичную нелинейности типа сухого трения. Следовательно, нелинейность типа «трехпозиционное реле» с гистерезисом является наиболее общим видом нелинейностей, имеющих характеристики с разрывом. е) Нелинейность типа «аналого-цифровой преобразователь»(рис. 4.14, е) представляет собой многопозиционную характеристику, которую имеют, например, проволочные потенциометрические измерительные преобразователи, аналого-цифровые преобразователи и др. Эта нелинейность имеет однозначную разрывную характеристику типа ступенчатой функции: где Следует отметить, что в данном параграфе рассмотрены лишь основные разновидности типовых нелинейностей. Кроме того, преобразователи СИ могут обладать одновременно несколькими типами нелинейностей, например насыщение с зоной нечувствительности, зазор и насыщение и т. д. Сравнивая общие свойства характеристик нелинейных элементов СИ, можно выделить две их особенности. Первая особенность заключается в своеобразии статических характеристик — наличии резких изломов, изгибов, разрывов непрерывностей и др. Вторая — в нарушении принципа суперпозиции. Реакция нелинейного элемента, например на единичное ступенчатое воздействие, будет зависеть от величины воздействия, а, следовательно, нелинейный элемент не будет иметь единственной передаточной функции. При этом становится невозможным использование преобразований Лапласа и Фурье при переходе из временной области в частотную и обратно. Таким образом, математические методы исследования нелинейных СИ должны располагать арсеналом для описания элементов как в статическом, так и в динамическом режимах и учитывать эти особенности при их анализе. Рассмотрим для примера составление уравнений датчика числа Маха (рис. 4.15). Число́ Ма́ха (M) — в механике сплошных сред — один из критериев подобия в механике жидкости и газа. Представляет собой отношение скорости течения в данной точке газового потока к местной скорости распространения звука в движущейся среде — назван по имени австрийского учёного Эрнста Маха. Датчик состоит из мембранной коробки 5, куда подается статическое давление рст, анероидной коробки 3, установленной на подвижной рамке 4, которая может поворачиваться вокруг оси, перпендикулярной к плоскости чертежа, па угол На основании выявленных преобразований можно построить структурную схему. Условие равновесия механического узла может быть записано как где Следовательно, рассматриваемая система будет существенно нелинейной ввиду наличия релейного элемента и нелинейной связи угла Уравнение движения исполнительного двигателя [11] имеет вид где Однако напряжение, а, следовательно, и момент где b, mb — углы поворота, соответствующие замыканию и размыканию контактов реле с учетом сухого трения. Дата добавления: 2015-11-18 ; просмотров: 2522 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ http://fizmathim.com/o-differentsialnyh-uravneniyah-sistem-gisterezisnogo-tipa http://helpiks.org/5-108738.htmlМАТЕМАТИЧЕСКИЕ МОДЕЛИ СРЕДСТВ ИЗМЕРЕНИЙ С УЧЕТОМ НЕЛИНЕЙНОСТЕЙ
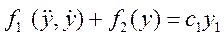
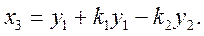
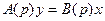
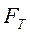
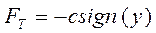
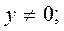
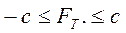
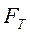
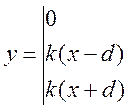
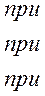
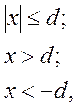
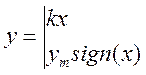
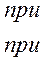
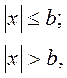
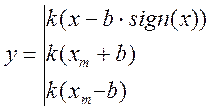
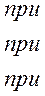
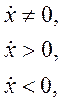
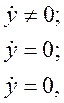
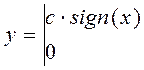
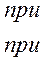
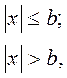
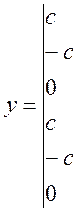
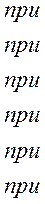
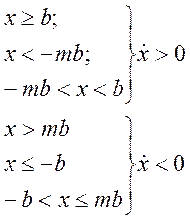
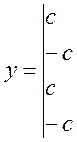
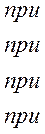
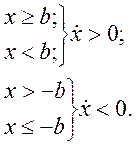
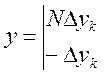
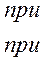
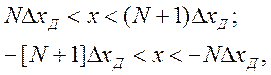
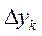
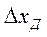
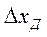
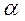
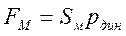
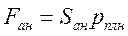
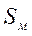
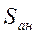
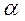
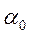
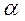
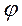
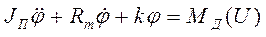
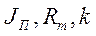
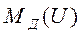
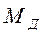
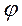
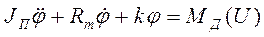
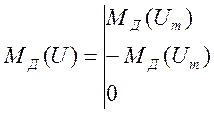
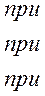
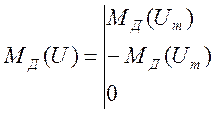
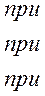
| следующая лекция ==> где Z, F, q — обобщенные сопротивление, сила, скорость. | Материальные ценности, созданные человеком.