Дифференциальные уравнения в технике презентация

Презентация на тему»Дифференциальные уравнения»

Дифференциа́льное уравне́ние — уравнение, связывающее значение производной функции с самой функцией, значениями независимой переменной, числами (параметрами). Порядок входящих в уравнение производных может быть различен (формально он ничем не ограничен). Производные, функции, независимые переменные и параметры могут входить в уравнение в различных комбинациях или все, кроме хотя бы одной производной, отсутствовать вовсе. Не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением. Например, 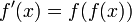не является дифференциальным уравнением. [источник?]

Дифференциальное уравнение порядка выше первого можно преобразовать в систему уравнений первого порядка, в которой число уравнений равно порядку исходного уравнения.

Современные быстродействующие ЭВМ эффективно дают численное решение обыкновенных дифференциальных уравнений, не требуя получения его решения в аналитическом виде. Это позволило некоторым исследователям утверждать, что решение задачи получено, если её удалось свести к решению обыкновенного дифференциального уравнения.

Презентация по математике на тему «Дифференциальные уравнения»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

Дифференциальные уравнения Основные определения

Определение: Дифференциальным уравнением (n)-ого порядка называется соотношение, связывающее независимую переменную х, функцию y, и её производные до (n)-ого порядка включительно. Определение: Наивысший порядок производной, входящий в уравнение называется порядком уравнения.

Определение: Всякая функция , которая, будучи подставленная в уравнение (1), обращает его в тождество, называется решением этого уравнения. Определение: Решить уравнение – значит, найти все его решения в заданной области.

Определение: Общим решением дифференциального уравнения называется такое его решение , которое содержит столько независимых постоянных, каков порядок этого уравнения. Если общее решение задано в неявном виде , то оно называется общим интегралом дифференциального уравнения.

Определение: Всякое решение дифференциального уравнения, которое получается из общего решения, если производным постоянным, в него входящим придать определенные значения, называется частным решением этого дифференциального уравнения.

Определение: Дифференциальным уравнением первого порядка называется уравнение . В простом случае y’=f(x,y). Дифференциальные уравнения первого порядка

Определение: Общим решением дифференциального уравнения первого порядка y’=f(x,y) в области D, называется функция , обладающая следующими свойствами: 1) Она является решением данного уравнения при любых значениях производной постоянной C, принадлежащих некоторому множеству. 2) Для любого начального условия y( )= такого, что ,существует единственное значение C= , при котором решение удовлетворяет заданному начальному условию.

Определение: Всякое решение , получающееся из общего решения , при конкретном C= называется частным решением. Определение задачи Коши: Задача, в которой требуется найти частное решение уравнения , удовлетворяющее начальному условию у( )= , называется задачей Коши. Определение: Общее решение , построенное на плоскости графика, называется интегральной кривой.

Геометрически — общее решение представляет собой семейство интегральных кривых , C — const(любая). Однако встречаются дифференциальные уравнения, имеющие также решения, которые не получаются из общего ни при каких значениях C (в том числе и при ). Такие решения называются особыми. Графиком особого решения является интегральная кривая, которая в каждой своей точке имеет общую касательную с одной из интегральных кривых, определяемых общим решением. Такая кривая называется огибающей семейства интегральных кривых.

Определение: Процесс нахождения решений дифференциального уравнения называется интегрированием дифференциального уравнения. Не существует общего метода решения дифференциального уравнения первого порядка.

Определение: Дано дифференциальное уравнение f(x,y, y’)=0. Пусть его можно переписать в виде , и т.к. , то уравнение примет вид: Переменные x и y равноправны. Уравнения первого порядка с разделяющимися переменными

Определение: Дифференциальное уравнение называется дифференциальным уравнением с разделяющимися переменными, если :

Метод решения: | :X(x)≠0 | :Y(y)≠0

Интегрируем обе части по х: y=y(x)  +  = 0 — общий интеграл уравнения, выраженный в новой форме.

Линейные дифференциальные уравнения первого порядка. Метод Бернулли.

Определение: Дифференциальные уравнения первого порядка вида a(x)y’+ +b(x)y+c(x)=0,где a,b,c – заданные функции, называется линейным дифференциальным уравнением первого порядка. Определение: Если a(x)≠0,то уравнение называется приведенным линейным уравнением первого порядка.

Определение: Если , то линейное уравнение называется неоднородным. y’+p(x)y=f(x) Определение: Если ,то уравнение y’+p(x)y=0 называется однородным и является относительно и y уравнением с разделяющимися переменными.

Решение методом Бернулли y ищем в виде произведения функции и , т.е. Найдем одну функцию такую, чтобы ; – любая, (≠0),так как только должно удовлетворять уравнению. …,в уравнение

(так как одна из функций ≠0); Уравнение с разделяющимися переменными:

Особых решений нет. Уравнение с разделяющимися переменными. Общее решение:

Определение: Дифференциальное уравнение первого порядка вида называется уравнением Бернулли. Метод решения: используем метод решения дифференциального уравнения первого порядка. Варьируем произвольную постоянную. Пусть . Найдем функцию из условия, что является решением неоднородного дифференциального уравнения. Уравнение Бернулли

Дано: уравнение первого порядка вида y’+p(x)*y=f(x) Алгоритм решения. Рассмотрим соответствующее однородное уравнение . Найдем его решение. Это уравнение с разделяющимися переменными. Метод вариации произвольной постоянной. Метод Лагранжа.

Определение: Функция f(x,y) называется однородной измерения M, если для любой . Определение: Уравнение вида называется однородным, если P и Q однородные функции одного измерения. Однородные дифференциальные уравнения

Теорема 1: Однородные дифференциальные уравнения первого порядка сводится к уравнению первого порядка с разделёнными переменными. С помощью подставим где , ( ).

Теорема 2: Дифференциальное уравнение y’=f(x,y) является однородным тогда и только тогда, когда f(x,y) есть однородная функция нулевого измерения.

Теорема существования и единственности решения. Особые решения.

Если в дифференциальном уравнении функция непрерывна в некоторой области D плоскости Oxy и имеет в этой области ограниченную частную производную , то для любой точки в некотором интервале существует притом единственное решение этого уравнения, удовлетворяющее начальному условию. Геометрически это означает, что через каждую точку M области D проходит одна и только одна интегральная кривая уравнения . Теорема Коши.

Определение: Точки области D, в котором нарушается единственность решения задачи Коши, называется особыми точками дифференциального уравнения. Определение: Решение (интегральная кривая) уравнения , в каждой точке которого нарушается единственность решения задачи Коши, называется особым решением (особой интегральной кривой) этого уравнения. Особое решение не может быть получено из общего, ни при каких значениях (включая ).

Графиком особого решения является огибающая семейства интегральных кривых, она находится путем исключения, если это возможно, параметра из системы уравнений. или — общий интеграл — общее решение дифференциального уравнения

Теорема существования и единственности решения задачи Коши для дифференциальных уравнения высших порядков

Определение: . Определение: Задачей Коши для дифференциальных уравнений: называется задача отыскания решения y=y(x), удовлетворяющего заданным начальным . условиям y(x0)=y0, y’(x0)=y0’,…,y(n-1)(x0)=y0(n-1).

Определение: Общим решением уравнения называется такая функция , которая при любых допустимых значениях параметров , является решением дифференциального уравнения и для любой задачи Коши с условиями y(x0)=x0, y ‘(x0)=y0’,…, y(n-1)(x0)=y0(n-1) найдутся постоянные . определяемые из системы уравнений.

Теорема: Существования и решения задачи Коши: Если дифференциальное уравнение таково, что функция в некоторой области D своих аргументов непрерывна и имеет непрерывные частные производные , то для любой точки принадлежащий D существует такой интервал , на котором существует и притом единственное решение этого уравнения, удовлетворяющее начальному условию.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 925 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 684 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 309 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 578 929 материалов в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Другие материалы

• 08.11.2017
• 4505
• 54

• 08.11.2017
• 355
• 1

• 08.11.2017
• 1208
• 7

• 08.11.2017
• 326
• 0

• 08.11.2017
• 507
• 3

• 08.11.2017
• 5605
• 25

• 08.11.2017
• 421
• 2

• 08.11.2017
• 11644
• 2214

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 08.11.2017 3635
• PPTX 623 кбайт
• 217 скачиваний
• Рейтинг: 3 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Соломахина Светлана Игоревна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 4 года и 4 месяца
• Подписчики: 5
• Всего просмотров: 43018
• Всего материалов: 31

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

В Курганской области дистанционный режим для школьников продлили до конца февраля

Время чтения: 1 минута

В Ленобласти школьники 5-11-х классов вернутся к очному обучению с 21 февраля

Время чтения: 1 минута

Приемная кампания в вузах начнется 20 июня

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Дифференциальные уравнения. Примеры задач приводимые к дифференциальным уравнениям. Дифференциальные уравнения с разделяющими переменными. 11 класс. — презентация

Презентация была опубликована 6 лет назад пользователемГеоргий Арапов

Похожие презентации

Презентация на тему: » Дифференциальные уравнения. Примеры задач приводимые к дифференциальным уравнениям. Дифференциальные уравнения с разделяющими переменными. 11 класс.» — Транскрипт:

1 Дифференциальные уравнения. Примеры задач приводимые к дифференциальным уравнениям. Дифференциальные уравнения с разделяющими переменными. 11 класс

2 Основные понятия Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функцию и производные(или дифференциалы) этой функции. Если независимая переменная одна, то уравнение называется обыкновенным; если же независимых переменных две или больше, то уравнение называется дифференциальным уравнением в частных производных.

3 Наивысший порядок производной, входящей в уравнение, называется порядком дифференциального уравнения. Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида:

4 Решением дифференциального уравнения называется такая дифференцируемая функция у=φ(х), которая при подстановке в уравнение вместо неизвестной функции обращает его в тождество. Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения.

5 Общим решением дифференциального уравнения первого порядка у / = f(x,y) в области D называется функция y=φ(x, C), обладающая следующими свойствами: 1)При любых значениях С она является решением данного уравнения,2) для любого условия (х 0, у 0 ) существует единственное значение С 0. Всякое решение y=φ(x, C 0 ),получающееся из общего решения y=φ(x, C) при конкретном значении С=С 0, называется частным решением.

6 Разделяют несколько типов (видов) обыкновенных дифференциальных уравнений: -Уравнения с разделяющимися переменными, -Однородные уравнения, -Линейные уравнения, -Уравнение в полных дифференциалах, -и т.д. Остановимся подробнее на каждом из этих типов уравнений.

7 Уравнения с разделёнными переменными. Так называются уравнения вида удовлетворяющее начальному условию f(x)dx + g(y)dy = 0, Интегрируя, получим — общий интеграл (общее решение) этого уравнения. Пример: — общее решение

8 Уравнения с разделяющимися переменными. Так называются уравнения вида Эти уравнения легко сводятся к уравнению с разделёнными переменными: Записываем уравнение в форме: затем делим на g(y) и умножаем на dx:. Это уравнение — с разделёнными переменными. Интегрируя, получим общий интеграл:

9 Алгоритм решения уравнений с разделяющимися переменными 1. Выражают производную функции через дифференциалы dx,dy. 2. Члены с одинаковыми дифференциалами переносят в одну сторону равенства и выносят дифференциал за скобку. 3. Разделяют переменные. 4. Интегрируют обе части равенства и находят общее решение. 5. Если заданы начальные условия, то находят частное решение.

10 Выразим у из последнего выражения как функцию х, получим общее решение : Пример:

11 Уравнения с однородной правой частью. Так называются уравнения со специальным видом зависимости функции f(x, y) от своих аргументов: Это уравнение сводится к уравнению с разделяющимися переменными относительно новой неизвестной функции u(x) заменой: Подставляя в уравнение y = x·u, y = u + x·u, получим (это — уравнение с разделяющимися переменными), — это общий интеграл уравнения относительно переменных x, u

12 Пример : — общее решение уравнения

13 Решение задач 1. Решить уравнение: у / =х+3 2. Найти решение у(х) дифференциального уравнения у / =cos(x), удовлетворяющее условию у(0)=1. 3. Найти уравнение линии, проходящей через точку М(1;3) и имеющей касательную, угловой коэффициент которой равен 2 х-3.

14 Решение задач 4. Скорость тела, выходящего из состояния покоя, равна 5t 2 м/с по истечении t секунд. Определите путь, который пройдет тело за 3 секунды. 5. Решить уравнение: хdx+ydy=0. 6. Составить уравнение движения тела по оси ОХ, если оно начало движение от точки М(4;0) со скоростью v =2t+3t Решить уравнение: 2ydy=3 х 2 dx.