Дифференциальные уравнения в жизни человека

Совершенно очевидно, что x(0) = m, откуда C = m. А теперь подставим это в уравнение выше и выразим время t через которое Ахиллес помрет (x(t) = 0):

t = \frac » alt=»\frac = m => t = \frac » src=»https://habrastorage.org/getpro/habr/upload_files/633/ea1/c3e/633ea1c3ed3fda6f8529296e5462f7d3.svg» width=»211″ height=»42″/>

Получилось просто и красиво, более того, есть задачи на которые можно дать ответ только с помощью дифференциальных уравнений. Например, если k зависит от времени. Давайте помечтаем немного и представим, что в какой-то момент времени наука развилась до такого уровня, что требуется все меньше и меньше времени для продления ожидаемой ПЖ на год, то есть k уменьшается со временем.

Пусть, например, k уменьшается по экспоненте с периодом полураспада в n лет. И давайте попробуем ответить на такой вопрос: какой должен быть минимальный m, чтобы человек мог достигнуть longevity escape velocity при таком k(t)?

Чтобы ответить на данный вопрос давайте составим дифференциальное уравнение:

Надо, пожалуй, пояснить откуда взялось b в экспоненте и чему равняется

Мы определили k(t) = k0*exp(-bt). Так как через n лет значение k(t) должно быть вдвое меньше, то имеем

e^ <-bt_0 + bt_0 + bn>= 2 => e^ = 2″ alt=»\frac>> = 2 => e^ <-bt_0 + bt_0 + bn>= 2 => e^ = 2″ src=»https://habrastorage.org/getpro/habr/upload_files/e67/61e/489/e6761e4899cc828438ff99ba705f8358.svg» width=»351″ height=»46″/>

b = \frac» alt=»bn = ln(2) => b = \frac» src=»https://habrastorage.org/getpro/habr/upload_files/23b/ca8/089/23bca8089b668a1c683f1b603da7bd80.svg» width=»187″ height=»40″/>

Интегрируем уравнение и получаем:

Чтобы определить C, воспользуемся начальным условием: x(0)=m:

m = \frac<1> + C => C = m — \frac<1>» alt=»x(0) = \frac<1> + C => m = \frac<1> + C => C = m — \frac<1>» src=»https://habrastorage.org/getpro/habr/upload_files/ab1/c06/595/ab1c065956c99b57d75eecef3838b590.svg» width=»394″ height=»40″/>

Получаем следующую запись функции дожития:

Давайте взглянем на ее график:

Функция x(t) имеет минимум и нам нужно, чтобы этот минимум был выше оси абсцисс (фиолетовая кривая)

Наша функция дожития имеет минимум и все, что нам нужно, это найти значение минимума как функции от m и найти значение m при котором этот минимум больше нуля. Как мы помним еще со школы, для того, чтобы найти минимум функции надо сначала найти ее производную и приравнять к нулю. Причем производную-то мы уже знаем из уравнения (1):

x'(t) = \frac> — 1 => t_ = \frac» alt=»dx =-dt + \fracdt> => x'(t) = \frac> — 1 => t_ = \frac» src=»https://habrastorage.org/getpro/habr/upload_files/bd1/52d/55d/bd152d55de03f1b1adefa44e83ab5972.svg» width=»419″ height=»44″/>

Мы точно знаем, что это минимум, потому что вторая производная положительна на всей области определения, а значит функция выпукла вниз и, следовательно, найденный экстремум является минимумом.

Теперь необходимо найти :

А отсюда уже выразим ограничение для m:

При и необходимо иметь в запасе примерно 9.2 года ожидаемой продолжительности жизни, чтобы достичь longevity escape velocity, то есть быть, например, мужчиной моложе 79 лет. Каждый может прикинуть свои шансы на достижение longevity escape velocity исходя из своего возраста. Но возможно ли в принципе бессмертие? Есть ли какие-то фундаментальные математические (не физические) ограничения? Об этом я расскажу в следующей статье, а пока давайте поговорим о более практических вещах.

Задача 2. Плазмаферез

Конечно, медицинская наука еще очень далека от достижения LEV (а может быть этого и вовсе никогда не случится), однако попытки отсрочить старение ведутся уже сейчас. Одной из самых интересных интервенций, возможно, способной немного продлить молодость и продолжительность жизни является терапевтическое разбавление плазмы. Известные геронтологи супруги Конбои продемонстрировали, что если мышкам заменить половину плазмы на физраствор с альбумином, то у них существенно улучшаются многие показатели жизнедеятельности. Предполагается, что это происходит за счет удаления из организма токсичных продуктов, которые образуются из-за старения организма. Более подробно все описано, например, тут. Более того, некоторые отчаянные биохакеры даже пробуют этот метод на себе и замечают улучшение ряда биомаркеров. Конечно, пройдет еще немало времени прежде чем установят эффективность (или неэффективность) этого метода на людях, но мы тем не менее постараемся ответить на вполне конкретный вопрос: а сколько раз нам необходимо сдать плазму, чтобы заменить половину, если за один раз забирается v мл?

Поскольку нам надо найти такой k при котором обновится половина плазмы, то приравняем правую часть уравнения выше к 1/2, прологарифмируем обе части равенства и воспользуемся свойствами логарифма, чтобы получить формулу для k:

-ln(2) = kln(1-\frac) => k = \frac<-ln(2)>)>» alt=»\frac<1> <2>= (1 — \frac)^k => -ln(2) = kln(1-\frac) => k = \frac<-ln(2)>)>» src=»https://habrastorage.org/getpro/habr/upload_files/106/f6f/e33/106f6fe3379b97d2644766ec593c8fd9.svg» width=»450″ height=»48″/>

Удельный объем плазмы взрослого мужчины составляет, в среднем, 46.7 мл/кг. Возьмем к примеру мужчину массой 80 кг и v=450 мл (стандартный объем плазмы при донорстве):

То есть взрослому сорокалетнему мужчине массой 80 кг необходимо за короткий срок 6 раз пожертвовать плазму, чтобы ее обновить чуть более чем наполовину.

Пусть X(t) — доля старой плазмы в момент времени t. Пусть скорость вытекания плазмы равна r мл/мин. Чему же будет равна концентрация старой плазмы в момент времени t + dt? А концентрация равна:

Давайте разберем каждое составляющее этого равенства:

X(t)V: концентрация старой плазмы помноженная на общий объем — очевидно это объем старой плазмы во всем организме в момент t

X(t)rdt: это объем старой плазмы, который вытечет за время dt (rdt — это скорость истечения, помноженная на время, что соответствует объему, а X(t) — это доля старой плазмы в этом объеме).

Затем мы делим получившийся объем старой плазмы на общий объем (который остается неизменным, потому что физраствор втекает с той же скоростью) и получим концентрацию. А теперь узнаем чему равно изменение концентрации (разница между концентрацией в моменты времени t+dt и t):

X(t + dt) — X(t) = — \fracrdt => dX = -\fracrdt» alt=»X(t + dt) = X(t) — \fracrdt => X(t + dt) — X(t) = — \fracrdt => dX = -\fracrdt» src=»https://habrastorage.org/getpro/habr/upload_files/e08/f0b/273/e08f0b27308748325ba95b8be3e93507.svg» width=»629″ height=»41″/>

Разделяем переменные и решаем это дифференциальное уравнение:

ln|X(t)| = -\frac+C_1″ alt=»\frac = -\frac =>ln|X(t)| = -\frac+C_1″ src=»https://habrastorage.org/getpro/habr/upload_files/ca3/f71/a95/ca3f71a9549601fdf87fad0d64256245.svg» width=»286″ height=»39″/>

Мы знаем, что вначале концентрация старой плазмы равнялась 1:
X(0) = 1 => C = 1

Поэтому , а теперь найдем время, за которое обновится половина плазмы:

-ln(2) = -\frac> => t_ <1/2>= \frac» alt=»\frac<1> <2>= e^<\frac<-rt_<1/2>>> => -ln(2) = -\frac> => t_ <1/2>= \frac» src=»https://habrastorage.org/getpro/habr/upload_files/714/ab6/82f/714ab682fd36fd7528ad1f1cbecf78d1.svg» width=»384″ height=»41″/>

На практике это означает примерно 259 минут (4 с лишним часа!), если руководствоваться средней скоростью 10 мл/мин (обычно забирают 450 мл плазмы и уходит на это примерно 45 минут):

Конечно, это время абсолютно неприемлемо, однако процедуру можно существенно ускорить. Например, в этой статье описан метод, который позволяет изымать плазму со скоростью 24 мл/мин, что позволяет заменить половину плазмы за 108 минут. Весьма неплохо! Однако неизвестно выдержит ли организм замену половины плазмы за один раз 🙂 Но это уже выходит за рамки математики, оставим этот вопрос врачам. Тем более, что различные клинические исследования по влиянию плазмафереза на старение людей уже начались.

Дифференциальные уравнения в жизни человека

Дифференциальные уравнения. Тезисы. Примеры применений.

Тип публикации: Тезисы

Язык: Русский

Enter the password to open this PDF file:

Григоренко М.Н., Уральский государственный экономический университет, г. Екатеринбург Дифференциальные уравнения и их применение Изучая разделы математики можно рассматривать решение задач с использованием математического аппарата, например таких как, методы расчета рисковых оптимального временного ситуаций, использования ряда [2]. Более выбор оптимального ресурсов, анализ подробно портфеля, и задачи прогнозирование рассмотрим применение дифференциальных уравнений. Дифференциальные уравнения — раздел математики, изучающий теорию и способы решения уравнений, содержащих искомую функцию и ее производные различных дифференциальные) или порядков одного нескольких аргумента аргументов (обыкновенные (дифференциальные уравнения в частных производных) [1]. В самом уравнении участвует не только неизвестная функция, но и различные ее производные. Дифференциальным уравнением описывается связь между неизвестной функцией и ее производными. Такие связи отыскиваются в различных областях знаний: в механике, физике, химии, биологии, экономике и др. Дифференциальные уравнения применяются для математического описания природных явлений. Так, например, в биологии дифференциальные уравнения применяются для описания популяции; в физике многие законы можно описать с помощью дифференциальных уравнений. Широкое применение находят дифференциальные уравнения и в моделях экономической динамики. В данных моделях отражается не только зависимость переменных от времени, но и их взаимосвязь во времени. Рассмотрим одну из задач макроэкономической динамики [1]. Например, пусть y(f) — объем продукции некоторой отрасли, реализованной к моменту времени t. Будем полагать, что вся производимая отраслью продукция реализуется по некоторой фиксированной цене р, т.е. выполнено условие ненасыщаемости рынка. Тогда доход к моменту времени t составит Y (t )  py(t ) Обозначим через I(t) величину инвестиций, направляемых на расширение производства. В модели естественного роста полагают, что скорость выпуска продукции (акселерация) пропорциональная величине инвестиций, т.е. y’ (t )  lI (t ) , где 1/l – норма акселерации. (Здесь мы пренебрегаем временем между окончанием производства продукции и ее реализацией, то есть считаем, что инвестиционный лаг равен нулю). Полагая, что величина инвестиций I(t) составляет фиксированную часть дохода, получим I (t )  mY (t )  mpy(t ) , где коэффициент пропорциональности m (так называемая норма инвестиций) — постоянная величина ( 0  m  1 ). Подставляя последнее выражение для I(t) в y’ (t )  lI (t ) приходим к уравнению y’  ky , где k  mpl . Полученное дифференциальное уравнение — с разделяющимися переменными. Решая его, приходим к функции y(t )  y0 e k ( t t0 ) , где y0  y(t 0 ) . Заметим, что уравнение y’  ky описывает также рост народонаселения, динамику роста цен при постоянной инфляции, процесс радиоактивного распада и др. Модель роста в условиях роста конкурентного рынка имеет вид y’ mlp( y) y . Научный руководитель Кныш А.А., старший преподаватель Список литературы: 1. Высшая математика для экономического бакалавриата: учебник и практикум / Н. Ш. Кремер, Б. А. Путко, И. М. Три-шин, М. Н. Фридман; под ред. Н. Ш. Кремера. – М.: Издательство Юрайт; ИД Юрайт, 2012. — 909 с. 2. Кныш А.А. Примеры реализации межпредметных связей на занятиях математики в экономическом вузе // Новая наука: от идеи к результату. — Стерлитамак: АМИ, 2017. — №2 (2) – С. 55 – 57.

Дифференциальные уравнения в жизни человека

Сразу расшифруем: на студенческом жаргоне дифуры – это дифференциальные уравнения. Часто студентам технических вузов бывает непонятно: зачем им преподают высшую математику? Учитывая тему статьи, ответ будет интересен тем курсантам, которым предстоит служить в войсках и участвовать в боевых действиях.

Понятно, надо знать работу специальных приборов и техники, но зачем высшая математика? Тем более, ни для кого не секрет, что нередко в вузах дают такие знания, которые в жизни никогда не оказываются востребованными.

Чтобы показать полезность знаний, в нашем случае высшей математики, приведём пример построения математической модели боевых действий.

Дополнительным аргументом в пользу нашей точки зрения служит универсальность математики. Имеется в виду то, что одни и те же уравнения часто годятся для описания совершенно разных процессов. Просто, математические символы могут обозначать разные вещи, притом, что решение задачи имеет одно и то же аналитическое выражение.

Модель, которую мы хотим вам предложить, годится как для военных (решение описывает изменение численности подразделения во время боевых действий), так и для описания апериодического процесса колебаний напряжения в электрическом контуре (это важно в задачах из областей связи и телекоммуникаций).

Фредерик Вильям Ланчестер (1868–1946) –
английский эрудит и инженер,
внёс значительный вклад
в автомобилестроение, аэродинамику,
был одним из основателей
теории исследования операций

Итак, ещё в начале прошлого века английский инженер Фредерик Вильям Ланчестер, во время Первой мировой войны, построил ряд математических моделей ведения воздушных сражений. Позже эти модели распространили на случаи боевых действий регулярных войск и партизанских соединений.

Рассмотрим ниже самую простую из таких моделей. Основа нашей модели – дифференциальное уравнение. Из названия уравнения видна необходимость знакомства с понятием производной функции (дифференцирование – это и есть взятие производной). Поэтому скажем об этом несколько слов (точнее, напомним, так как эти понятия входят в школьную программу).

Понятие производной напомним с помощью примера. Если известно, как пройденный телом путь зависит от времени, то мгновенная скорость тела в каждой точке пути как раз и есть производной от пути по времени. Другими словами, мгновенная скорость есть отношение очень малого пути ко времени, за которое тело его проходит (понятно, что и время, соответствующее этому пути, тоже очень мало).

Так, решением алгебраического квадратного уравнения являются два числа (если решение возможно). А вот если уравнение в качестве неизвестной содержит функцию времени и её производные, то такое уравнение называется дифференциальным.

Его решением уже является неограниченно много чисел – целая функция. Тут, правда, надо ещё добавить начальные условия, то есть значения неизвестной функции и её производных меньшего порядка, чем есть в уравнении, в определённый момент времени.

Теперь мы можем рассмотреть нашу модель.

Основная задача нашей модели – выяснить, как меняется численность воюющих сторон со временем при некоторых начальных условиях, о которых скажем ниже. Итак, пусть в боевых действиях участвуют две противоборствующие стороны. Их численный состав обозначим через x(t) и y(t). Начало боевых действий пусть соответствует моменту t = 0 дней.

На деле трудно указать критерии, которые учитывали бы при сравнении противников степень боевой готовности и качество вооружения, способности и опыт командного состава, моральный дух и многие другие факторы. Поэтому сделаем некоторые упрощающие предположения.

Пусть x(t) и y(t) меняются непрерывно и, более того, эти функции имеют производные по времени. Конечно, это упрощение реальной ситуации, поскольку как x(t), так и y(t) – число военных, то есть целое число. Но понятно, что при достаточно больших численных составах каждого из противников увеличение их численности на одного или двух человек даёт на деле очень малую величину по сравнению со всем личным составом.

Поэтому можно считать, что за малые промежутки времени численный состав также изменяется на малые (и даже не целые) количества. Это даст нам возможность искать решение в виде непрерывной функции, что очень упрощает поиск.

Этих соглашений, конечно, недостаточно для того, чтобы выписать конкретные формулы для x(t) и y(t) как функций времени t. Однако, можно указать ряд факторов, которые позволяют описать скорости изменения численности противников.

Обозначим через v_mх – скорость, с которой сторона х несёт потери от болезней и других факторов, не связанных с боевыми действиями.

Далее, пусть v_wу – скорость, с которой сторона х несёт потери во время ведения боевых действий со стороной у. Аналогичные обозначения введём для у. Тогда ясно, что скорости изменения x(t) и y(t) можно задать уравнениями

Теперь надо как-то связать эти скорости v_m и v_w с количествами x и y. После чего можно исследовать полученные дифференциальные уравнения, и анализ решения позволит получить сведения о вероятном победителе.

Предположим, что v_mх = – ax(t) (это значит, что чем большей является численность войск х, тем больше военных могут выйти из строя по болезни, и скорость dx/dt уменьшится). Кроме того, допустим, что v_wу = – by(t) (то есть, численность х уменьшится под огнём противника пропорционально его численности y). Тогда изменения x(t) можно описать уравнением

Для численности у можно написать аналогичное уравнение.

В уравнениях (1) и (2) а, b, с, d – неотрицательные постоянные, характеризующие степень влияния различных факторов на потери в живой силе обеих сторон х и у. Из них за непосредственные боевые действия отвечают только постоянные b, с. Ещё примем начальные условия: x_о и у_o – численный состав сил х и у в начале боевых действий.

Итак, пусть подразделения противника находятся в зоне действия огневых средств другой стороны, и огонь ведётся только по живой силе, непосредственно участвующей в боевых действиях. Понятно, что совсем непросто вычислить коэффициенты b и с. Один из путей найти их – это представить в виде

где r_у и r_х – удельные коэффициенты огневой мощи сторон у и х (доля огневой мощи, приходящаяся на одного бойца), а р_у и р_х – вероятности того, что каждый из выстрелов со стороны у или х окажется метким.

Отметим далее, что члены, которые соответствуют боевым потерям в уравнениях (1) и (2), являются линейными. Заметим, что Ф. Ланчестер рассматривал и нелинейные модели, которые позволяют описать много интересных особенностей военных действий, но мы для начального знакомства ограничимся линейной моделью.

Предположим, что регулярные войска противников ведут боевые действия в упрощённой ситуации, когда потери, не связанные с боевыми действиями, отсутствуют. Если при этом обе стороны ещё и не получают подкреплений, то математическая модель сводится к системе дифференциальных уравнений

Разделив второе уравнение на первое, получим

Интегрируя последнее уравнение (4) с учетом начальных условий, приходим к равенству

Соотношение (5) объясняет, почему систему (3) называют моделью с квадратичным законом. Если обозначить через К постоянную by_о 2 – cx_о 2 , то уравнение

Рис. 1

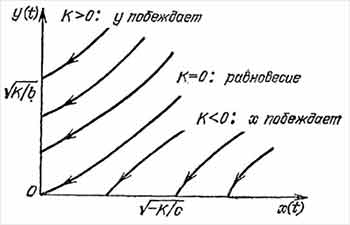
описывает гиперболу (или пару прямых при К = 0). Такую систему можно назвать дифференциальной системой с гиперболическим законом.

На рис. 1 изображены гиперболы для различных значений К, при этом ясно, что следует рассматривать лишь первый квадрант (так как х ≥ 0 и у ≥ 0). Стрелки на кривых указывают направление изменения численности сил с течением времени.

Чтобы ответить на вопрос, кто побеждает в построенной модели (3), условимся, прежде всего, говорить, что побеждает сторона у (или х), если она первой уничтожает боевые силы стороны х (или у). Так, в случае, если К > 0, побеждает сторона у, ибо в соответствии с уравнением (5) переменная у никогда не обращается в нуль, в то время как при значении y = (K/b) 1/2 переменная х обращается в нуль. Таким образом, чтобы победили силы у, им нужно стремиться достичь такой ситуации, при которой К > 0, то есть, когда

Из равенств (2) следует, что неравенство (7) можно переписать в виде

Левая часть этого неравенства показывает, что изменения в отношении сил y_о/x_о дают преимущество одной из сторон в соответствии с квадратичным законом! Так, например, изменение в отношении сил от y_о/x_о = 1 до y_о/x_о = 2 даёт четырехкратное преимущество силам у. Отметим правда, что уравнение (5) определяет соотношение между силами противников, не учитывая их зависимости от времени.

На всё, о чем выше было написано, автора вдохновила замечательная популярная книжка В.В. Амелькина «Дифференциальные уравнения в приложениях». Но в рамках нашей темы, как раз при построении временной зависимости для численности войск в рассмотренном в книге примере была допущена досадная, но существенная ошибка.

Перед тем, как продолжить чтение, попробуйте самостоятельно обнаружить эту ошибку. Хочу подчеркнуть, что эта ошибка нисколько не снижает ценности книги, к тому же написанной понятным языком, доступно для школьника, интересующегося математикой. Ниже приводится правильное решение.

Чтобы вывести формулы для временной зависимости численных составов, поступим следующим образом. Продифференцируем по t первое из уравнений системы (3) и подставим в него второе уравнение этой же системы. В результате придём к дифференциальному уравнению второго порядка, так называют уравнения, которые содержат вторую производную от неизвестной функции

Используя тогда в качестве начальных условий соотношения

получим решение уравнения (9) в виде

где chх = (е х +е –х )/2 и shх = (е х – е –х )/2 – гиперболические функции, b = (bc) 1/2 , g = (b/c) 1/2 . Эти функции напоминают тригонометрические (например, ch 2 х – sh 2 х = 1). Но cosx и sinx имеют колебательный характер, а chх и shх экспоненциально растут или падают, как это видно из их графиков на рис. 2 (график функции у = sh х) и 3 (график функции у = ch х). В вышеназванной книге выписаны решения другого уравнения – d 2 x/dt 2 + bсx = 0, а это – cosx и sinx.

Подобно формуле (10), можно получить решение для y(t) (сделайте это самостоятельно) в виде

На рис. 4 показаны графики функций, заданных уравнениями (10) и (11), в случае, когда К > 0 (т. е. когда by_о 2 > cx_о 2 или когда γy_о > x_о).

В заключение отметим, что для победы сил стороны у не обязательно, чтобы число y_о было больше числа x_о. Требуется лишь выполнение неравенства γy_о > x_о.

Если теперь под х(t) и у(t) понимать заряд q и электрический ток I = dq/dt, то мы придём к описанию апериодического процесса в электрической цепи. Более сложными и более соответствующими описываемому событию являются нелинейные модели.

Например, уравнение dN/dt = aN – bN 2 – основа дифференциальной модели популяций, которая связана с размножением или вымиранием животных, а также с сосуществованием различных их видов в ситуации «хищник – жертва».

Мы коснулись надводной части айсберга с именем «теория дифференциальных уравнений», которая на рубеже тысячелетий претерпела основательные изменения. Ничего не было сказано о нелинейной динамике, детерминированном хаосе и многом другом, что привело к новому пониманию необычных природных явлений.

Одним из таких явлений природы стала турбулентность, отражающая качественный переход к другой форме движения. В этом явлении и сегодня остаётся много загадок. Видимо, ещё не всё открыто, и молодому поколению есть, где приложить силы в познании окружающего мира.

А.М. Пальти , преподаватель физики