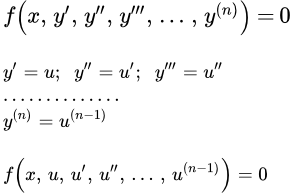Дифференциальные уравнения второго порядка не содержащие функции

Дифференциальные уравнения, приводимые к уравнениям первого порядка

Вы будете перенаправлены на Автор24

Дифференциальные уравнения второго порядка, в которых правая часть не зависит от неизвестной функции и её производной

Таким дифференциальным уравнением второго порядка является уравнение вида $y»=f\left(x\right)$. В нем правая часть не зависит от неизвестной функции $y$ и её производной $y’$, а зависит только от $x$. Решается это уравнение последовательным интегрированием.

Представим его в таком виде: $\frac \left(y’\right)=f\left(x\right)$, откуда $d\left(y’\right)=f\left(x\right)\cdot dx$.

Интегрируем первый раз, используя то свойство, что неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной: $\int d\left(y’\right) =\int f\left(x\right)\cdot dx $ или $y’=\int f\left(x\right)\cdot dx +C_ <1>$, где $C_ <1>$ — произвольная постоянная.

Таким образом, дифференциальное уравнение второго порядка сведено теперь к дифференциальному уравнению первого порядка, которое можно представить в таком виде: $dy=\left(\int f\left(x\right)\cdot dx +C_ <1>\right)\cdot dx$.

Интегрируем полученное дифференциальное уравнение повторно: $y=\int \left(\int f\left(x\right)\cdot dx +C_ <1>\right)\cdot dx =\int \left(\int f\left(x\right)\cdot dx \right)\cdot dx +\int C_ <1>\cdot dx$. Окончательно получаем:$y=\int \left(\int f\left(x\right)\cdot dx \right)\cdot dx +C_ <1>\cdot x+C_ <2>$, где $C_ <2>$ — произвольная постоянная.

Процесс интегрирования завершен. Получена неизвестная функция $y$, которая является общим решением данного дифференциального уравнения второго порядка.

Алгоритм решения дифференциального уравнения второго порядка $y»=f\left(x\right)$ может быть представлен в следующем виде:

1. находим интеграл $I_ <1>\left(x\right)=\int f\left(x\right)\cdot dx $ и записываем первую производную искомой функции в виде $y’\left(x,C_ <1>\right)=I_ <1>\left(x\right)+C_ <1>$;
2. находим интеграл $I_ <2>\left(x\right)=\int I_ <1>\left(x\right)\cdot dx $ и записываем окончательно общее решение данного дифференциального уравнения: $y=I_ <2>\left(x\right)+C_ <1>\cdot x+C_ <2>$;
3. для поиска частного решения начальные условия подставляем в выражение для первой производной $y’$, а также в общее решение; в результате находим значения произвольных постоянных $C_ <1>$ и $C_ <2>$.

Готовые работы на аналогичную тему

Найти общее решение дифференциального уравнения второго порядка $y»=4$. Записать также его частное решение, которое удовлетворяет начальным условиям $y=1$ при $x=1$, $y’=1$ при $x=1$.

В данном дифференциальном уравнении правая часть не зависит ни от неизвестной функции $y$, ни от её производной $y’$. Следовательно, оно решается последовательным интегрированием два раза подряд.

Находим интеграл $I_ <1>\left(x\right)=\int f\left(x\right)\cdot dx =\int 4\cdot dx =4\cdot x$. Записываем выражение для первой производной в виде $y’\left(x,C_ <1>\right)=I_ <1>\left(x\right)+C_ <1>$, то есть $y’=4\cdot x+C_ <1>$.

Находим интеграл $I_ <2>\left(x\right)=\int I_ <1>\left(x\right)\cdot dx =\int 4\cdot x\cdot dx =2\cdot x^ <2>$. Записываем окончательно общее решение в виде $y=I_ <2>\left(x\right)+C_ <1>\cdot x+C_ <2>$. Получаем: $y=2\cdot x^ <2>+C_ <1>\cdot x+C_ <2>$.

Ищем частное решение. Подставляем начальное условие $y’=1$ при $x=1$ в выражение для $y’$: $1=4\cdot 1+C_ <1>$, откуда $C_ <1>=-3$. Подставляем начальное условие $y=1$ при $x=1$ в выражение для $y$: $1=2\cdot 1^ <2>+\left(-3\right)\cdot 1+C_ <2>$, откуда $C_ <2>=2$. Таким образом, частное решение имеет вид: $y=2\cdot x^ <2>-3\cdot x+2$.

Дифференциальные уравнения второго порядка, не содержащие неизвестной функции

Указанные дифференциальные уравнения второго порядка допускают понижение порядка посредством замены переменных. После этого к полученным дифференциальным уравнениям первого порядка могут быть применены известные методы решения.

Дифференциальное уравнение второго порядка, не содержащее неизвестной функции $y$, имеет вид $y»=f\left(x,y’\right)$.

Для его решения применяют замену $y’=z\left(x\right)$.

При этом $y»=z’\left(x\right)$. После подстановки данное дифференциальное уравнение приобретает вид дифференциального уравнения первого порядка относительно $z$, то есть $z’=f\left(x,z\right)$. Решая его, находим $z\left(x\right)=\phi \left(x,C_ <1>\right)$.

В свою очередь, поскольку $y’=z\left(x\right)$, то $y’=\phi \left(x,C_ <1>\right)$. Это также дифференциальное уравнение первого порядка, которое допускает непосредственное интегрирование. Следовательно, интегрируя еще раз, окончательно получаем общее решение $y=\int \phi \left(x,C_ <1>\right)\cdot dx +C_ <2>$.

Алгоритм решения дифференциального уравнения второго порядка $y»=f\left(x,y’\right)$ может быть представлен в следующем виде:

1. переписываем данное дифференциальное уравнение в виде дифференциального уравнения первого порядка относительно переменной $z$, формально заменив $y»$ на $z’$, а $y’$ — на $z$;
2. полученное дифференциальное уравнение первого порядка решаем одним из подходящих известных методов;
3. найденное решение $z=\phi \left(x,C_ <1>\right)$ представляем в виде дифференциального уравнения первого порядка $y’=\phi \left(x,C_ <1>\right)$, которое допускает непосредственное интегрирование;
4. находим интеграл $I=\int \phi \left(x,C_ <1>\right)\cdot dx $ и получаем общее решение в виде $y=I+C_ <2>$.

Найти общее решение дифференциального уравнения$y»-\frac =3\cdot x$.

Данное дифференциальное уравнение не содержит неизвестной функции $y$, поэтому переписываем его в виде дифференциального уравнения первого порядка относительно переменной $z$, формально заменив $y»$ на $z’$, а $y’$ — на $z$. Получаем: $z’-\frac =3\cdot x$.

Это дифференциальное уравнение первого порядка является линейным неоднородным, решая которое известным методом, получаем $z=\left(3\cdot x+C_ <1>\right)\cdot x$.

Найденное решение представляем в виде дифференциального уравнения первого порядка $y’=\phi \left(x,C_ <1>\right)$, то есть $y’=\left(3\cdot x+C_ <1>\right)\cdot x$. Это дифференциальное уравнение допускает непосредственное интегрирование.

Находим интеграл $I=\int \phi \left(x,C_ <1>\right)\cdot dx =\int \left(3\cdot x+C_ <1>\right)\cdot x\cdot dx =x^ <3>+C_ <1>\cdot \frac > <2>$ и получаем общее решение в виде $y=I+C_ <2>=x^ <3>+C_ <1>\cdot \frac > <2>+C_ <2>$. Это общее решение можно представить также в виде $y=x^ <3>+C_ <1>\cdot x^ <2>+C_ <2>$.

Дифференциальные уравнения второго порядка, не содержащие независимой переменной

Указанные дифференциальные уравнения второго порядка также допускают понижение порядка посредством замены переменных. После этого к полученным дифференциальным уравнениям первого порядка могут быть применены известные методы решения.

Дифференциальное уравнение второго порядка, не содержащее независимой переменной $x$, имеет вид $y»=f\left(y,y’\right)$.

Для его решения применяют замену $y’=z\left(y\right)$.

Подставляем выражения для $y’$ и $y»$ в данное дифференциальное уравнение: $z\cdot \frac =f\left(y,z\right)$. Получили дифференциальное уравнение первого порядка относительно переменной $z$, которая является функцией $y$. Решая его, находим $z\left(y\right)=\phi \left(y,C_ <1>\right)$.

В свою очередь, поскольку $\frac =z\left(y\right)$, то $\frac =\phi \left(y,C_ <1>\right)$. Полученное дифференциальное уравнение представляет собой дифференциальное уравнение первого порядка с разделяющимися переменными, общее решение которого можно найти из выражения $\int \frac <\phi \left(y,C_<1>\right)> =x+C_ <2>$.

Алгоритм решения дифференциального уравнения второго порядка $y»=f\left(y,y’\right)$ может быть представлен в следующем виде:

1. переписываем данное дифференциальное уравнение в виде дифференциального уравнения первого порядка относительно переменной $z$, формально заменив $y»$ на $z\cdot z’$, а $y’$ — на $z$;
2. полученное дифференциальное уравнение первого порядка решаем одним из подходящих известных методов;
3. найденное решение $z=\phi \left(y,C_ <1>\right)$ представляем в виде дифференциального уравнения первого порядка $\frac=\phi \left(y,C_ <1>\right)$, которое является дифференциальным уравнением с разделяющимися переменными;
4. находим интеграл $I=\int \frac<\phi \left(y,C_<1>\right)> $ и получаем общее решение в виде $I=x+C_ <2>$.

Дифференциальные уравнения, допускающие понижение порядка

Рассмотрим три частных случая решения дифференциальных уравнений с возможностью понижения порядка. Во всех случаях понижение порядка производится с помощью замены переменной. То есть, решение дифференциального уравнения сводится к решению уравнения более низкого порядка. В основном мы рассмотрим способы понижения порядка дифференциальных уравнений второго порядка, однако их можно применять многократно и понижать порядок уравнений изначально более высокого порядка. Так, в примере 2 решается задача понижения порядка дифференциального уравнения третьего порядка.

Понижение порядка уравнения, не содержащего y и y‘

Это дифференциальное уравнение вида . Произведём замену переменной: введём новую функцию и тогда . Следовательно, и исходное уравнение превращается в уравнениие первого порядка

с искомой функцией .

Решая его, находим . Так как , то .

Отсюда, интегрируя ещё раз, получаем решение исходного уравнения:

,

где и — произвольные константы интегрирования.

Пример 1. Найти общее решение дифференциального уравнения

.

Решение. Произведём замену переменной, как было описано выше: введём функцию и, таким образом, понизив порядок уравнения, получим уравнение первого порядка . Интегрируя его, находим . Заменяя на и интегрируя ещё раз, находим общее решение исходного дифференциального уравнения:

Пример 2. Решить дифференциальное уравнение третьего порядка

.

Решение. Дифференциальное уравнение не содержит y и y‘ в явном виде. Для понижения порядка применяем подстановку:

.

Тогда и получаем линейное дифференциальное уравнение первого порядка:

.

Заменяя z произведением функций u и v , получим

Тогда получим выражения с функцией v :

Выражения с функцией u :

Дважды интегрируем и получаем:

.

.

Интегрируем по частям и получаем:

.

Итак, общее решение данного дифференциального уравения:

.

Понижение порядка уравнения, не содержащего y

Это дифференциальное уравнение вида . Произведём замену переменной как в предыдущем случае: введём , тогда , и уравнение преобразуется в уравнение первого порядка . Решая его, найдём . Так как , то . Отсюда, интегрируя ещё раз, получаем решение исходного уравнения:

,

где и — произвольные константы интегрирования.

Пример 3. Найти общее решение дифференциального уравнения

.

Решение. Уже знакомым способом произведём замену переменной: введём функцию и понизим порядок уравнения. Получаем уравнение первого порядка . Решая его, находим . Тогда и получаем решение исходного дифференциального уравнения второго порядка:

.

Пример 4. Решить дифференциальное уравнение

.

Решение. Дифференциальное уравнение не содержит y в явном виде. Поэтому для понижения порядка применяем подстановку:

.

Получим дифференциальное уравнение первого порядка:

.

Это уравение с разделяющимися переменными. Решим его:

Интегрируем полученную функцию:

Мы пришли к цели — общему решению данного дифференциального уравения:

.

Пример 5. Найти общее решение дифференциального уравнения

.

Решение. Дифференциальное уравнение не содержит y в явном виде. Поэтому для понижения порядка применяем подстановку:

.

Получим дифференциальное уравнение первого порядка:

.

Это однородное уравение, которое решается при помощи подстановки . Тогда , :

Далее потребуется интегрировать по частям. Введём обозначения:

Таким образом, получили общее решение данного дифференциального уравения:

.

Понижение порядка уравнения, не содержащего x

Это уравнение вида . Вводим новую функцию , полагая . Тогда

.

Подставляя в уравнение выражения для и , понижаем порядок уравнения. Получаем уравнение первого порядка относительно z как функции от y:

.

Решая его, найдём . Так как , то . Получено дифференциальное уравнение с разделяющимися переменными, из которого находим общее решение исходного уравнения:

,

где и — произвольные константы интегрирования.

Пример 6. Найти общее решение дифференциального уравнения

.

Решение. Полагая и учитывая, что , получаем . Понизив порядок исходного уравнения, получаем уравнение первого порядка с разделяющимися переменными. Приводя его к виду и интегрируя, получаем , откуда . Учитывая, что , находим , откуда получаем решение исходного дифференциального уравнения второго порядка:

.

При сокращении на z было потеряно решение уравнения , т.е. . В данном случае оно содержится в общем решении, так как получается из него при (за исключением решения y = 0).

Пример 7. Найти общее решение дифференциального уравнения

.

Решение. Дифференциальное уравнение не содержит x в явном виде. Для понижения порядка применяем подстановку:

.

Получим дифференциальное уравнение первого порядка:

.

Это уравение с разделяющимися переменными. Решим его:

Используя вновь подстановку

,

получим ещё одно уравнение с разделяющимися переменными. Решим и его:

Таким образом, общее решение данного дифференциального уравения:

.

Пример 8. Найти частное решение дифференциального уравнения

,

удовлетворяющее начальному условию y(0) = 1 , y‘(0) = −1 .

Решение. Дифференциальное уравнение не содержит x в явном виде. Поэтому применяем подстановку:

.

Таким образом, понизили порядок уравнения и получили уравнение первого порядка

.

Это дифференциальное уравнение с разделяющимися переменными. Разделяем переменные и интегрируем:

Чтобы определить C 1 , используем данные условия y(0) = 1 , y‘(0) = −1 или p(0) = −1 . В полученное выражение подставим y = 1 , p = −1 :

.

.

Разделяя переменные и интегрируя, получаем

.

Из начального условия y(0) = 1 следует

.

Получаем окончательное решение данного дифференциального уравнения

.

Пример 9. Найти частное решение дифференциального уравнения

,

удовлетворяющее начальному условию y(1) = 1 , y‘(1) = −1 .

Решение. Дифференциальное уравнение не содержит x в явном виде. Для понижения порядка применяем подстановку:

.

Таким образом, получили уравнение первого порядка

.

Это дифференциальное уравнение с разделяющимися переменными. Разделив обе части уравнения на p , получим

Интегрируем обе части уравнения

Используем начальные условия и определим C 1 . Если x = 1 , то y = 1 и p = y‘ = −1 , поэтому

.

Из начального условия y(1) = 1 следует

.

Получаем окончательное решение данного дифференциального уравнения

.

Дифференциальные уравнения высших порядков, не содержащие функцию в явном виде

Метод решения

Рассмотрим уравнение, не содержащие функцию в явном виде:
(1) .
Порядок этого уравнения понижается на единицу с помощью подстановки
.

Действительно, тогда:
;
;
.
.
И мы получили уравнение, в котором порядок понижен на единицу:
.

Пример

Делаем подстановку:
.
Тогда:
.
Подставляем:
.

Разделяем переменные:
.
При u ≠ 0 имеем:
.

Интегрируем:
.
Интегрируем еще раз:
.

Окончательно имеем:
.
Заменим постоянную:
.
Тогда
.

Теперь рассмотрим случай:
.
также является решением исходного уравнения. Интегрируем:
;
.

Автор: Олег Одинцов . Опубликовано: 17-07-2013