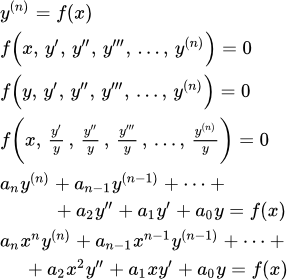Дифференциальные уравнения высшего порядка конспект

Лекция 14. Дифференциальные уравнения высших порядков

Дифференциальное уравнение n – ого порядка в общем виде записывается так:

.

Дифференциальное уравнение n – ого порядка в виде, разрешенном относительно старшей производной, выглядит так:

.

Решением дифференциального уравнения n – ого порядка называется функция , обращающая его в тождество.

Общим решением дифференциального уравнения n – ого порядка называется функция такая, что

1. при любом наборе констант эта функция является решением,

2. для любого набора начальных условий из области существования решения найдется набор констант , при котором функция удовлетворяет заданным начальным условиям, т.е. .

Заметим, что общее решение дифференциального уравнения n – ого порядка зависит ровно от n констант.

Частным решением дифференциального уравнения n – ого порядка называется какое-либо из решений, входящих в общее решение (при конкретном выборе констант).

Общим интегралом дифференциального уравнения n – ого порядка называется функция , сохраняющая свои значения на решениях дифференциального уравнения.

Интегральной кривой называется график частного решения.

Общее решение представляет собой совокупность интегральных кривых.

Обычно рассматривается одна из трех задач:

1. Найти общее решение дифференциального уравнения n – ого порядка,

2. Задача Коши – найти частное решение дифференциального уравнения n – ого порядка, удовлетворяющее заданным начальным условиям,

3. Краевая задача – найти частное решение, удовлетворяющее заданным начальным условиям, одна часть которых задана в точке , а другая часть в точке .

Теорема Коши (существования и единственности решения задачи Коши для дифференциального уравнения n – ого порядка ).

Пусть функция и ее частные производные по переменным определены и непрерывны в некоторой области .

Тогда для любой внутренней точки существует единственное решение дифференциального уравнения, удовлетворяющее этим начальным условиям, т.е.

(через любую внутреннюю точку проходит единственная интегральная кривая).

Пример. Рассмотрим дифференциальное уравнение второго порядка . Область существования и единственности решения заполнена непересекающимися интегральными кривыми. Через любую точку проходит единственная интегральная кривая. Однако через «точку» проходит бесконечно много интегральных кривых, все они различаются значениями . Заметим, что в «точка» представляет собой прямую .

Понижение порядка дифференциальных уравнений.

Мы умеем аналитически решать всего пять типов дифференциальных уравнений первого порядка: с разделяющимися переменными, однородные, линейные, Бернулли, в полных дифференциалах. Причем однородные, линейные и Бернулли тоже сводятся к уравнениям с разделяющимися переменными.

Даже решить уравнение второго порядка, не говоря уж об уравнении n-го порядка – проблема. Поэтому стараются понизить порядок дифференциального уравнения, если это возможно, чтобы свести его к известным типам уравнений первого порядка.

Если правая часть дифференциального уравнения n-го порядка зависит только от x, то интегрируя его n раз, можно получить решение.

.

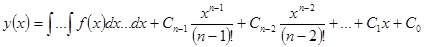
Но это – очевидный случай. Рассмотрим менее очевидные случаи.

Лекция на тему: «Дифференциальные уравнения второго порядка и высших порядков.»

Просмотр содержимого документа
«Лекция на тему: «Дифференциальные уравнения второго порядка и высших порядков.»»

Дифференциальные уравнения второго порядка и высших порядков.
Линейные ДУ второго порядка с постоянными коэффициентами.
Примеры решений.

Переходим к рассмотрению дифференциальных уравнений второго порядка и дифференциальных уравнений высших порядков. Если Вы смутно представляете, что такое дифференциальное уравнение (или вообще не понимаете, что это такое), то рекомендую начать с урока Дифференциальные уравнения первого порядка. Примеры решений. Многие принципы решения и базовые понятия диффуров первого порядка автоматически распространяются и на дифференциальные уравнения высших порядков, поэтому очень важно сначала разобраться с уравнениями первого порядка.

У многих читателей может быть предубеждение, что ДУ 2-го, 3-го и др. порядков – что-то очень трудное и недоступное для освоения. Это не так. Научиться решать диффуры высшего порядка вряд ли сложнее, чем «обычные» ДУ 1-го порядка. А местами – даже проще, поскольку в решениях активно используется материал школьной программы.

Наиболее популярны дифференциальные уравнения второго порядка. В дифференциальное уравнение второго порядка обязательно входит вторая производная и не входят производные более высоких порядков:

Следует отметить, что некоторые из малышей (и даже все сразу) могут отсутствовать в уравнении, важно, чтобы дома был отец . Самое примитивное дифференциальное уравнение второго порядка выглядит так:

Дифференциальные уравнения третьего порядка в практических заданиях встречаются значительно реже, по моим субъективным наблюдениям в Государственную Думу они бы набрали примерно 3-4% голосов.

В дифференциальное уравнение третьего порядка обязательно входит третья производная и не входят производные более высоких порядков:

Самое простое дифференциальное уравнение третьего порядка выглядит так: – папаша дома, все дети на прогулке.

Аналогичным образом можно определить дифференциальные уравнения 4-го, 5-го и более высоких порядков. В практических задачах такие ДУ проскакивают крайне редко, тем не менее, я постараюсь привести соответствующие примеры.

Дифференциальные уравнения высших порядков, которые предлагаются в практических задачах, можно разделить на две основные группы.

1) Первая группа – так называемые уравнения, допускающие понижение порядка. Налетайте!

2) Вторая группа – линейные уравнения высших порядков с постоянными коэффициентами. Которые мы начнем рассматривать прямо сейчас.

Линейные дифференциальные уравнения второго порядка
с постоянными коэффициентами

В теории и практике различают два типа таких уравнений – однородное уравнение инеоднородное уравнение.

Однородное ДУ второго порядка с постоянными коэффициентами имеет следующий вид:
, где и – константы (числа), а в правой части – строго ноль.

Неоднородное ДУ второго порядка с постоянными коэффициентами имеет вид:
, где и – константы, а – функция, зависящая только от «икс». В простейшем случае функция может быть числом, отличным от нуля.

Какая мысль приходит в голову после беглого взгляда? Неоднородное уравнение кажется сложнее. На этот раз первое впечатление не подводит!

Кроме того, чтобы научиться решать неоднородные уравнения необходимо уметь решать однородные уравнения. По этой причине сначала рассмотрим алгоритм решения линейного однородного уравнения второго порядка:

Для того чтобы решить данное ДУ, нужно составить так называемое характеристическое уравнение:

По какому принципу составлено характеристическое уравнение, отчётливо видно:
вместо второй производной записываем ;
вместо первой производной записываем просто «лямбду»;
вместо функции ничего не записываем.

– это обычное квадратное уравнение, которое предстоит решить.

Существуют три варианта развития событий. Они доказаны в курсе математического анализа, и на практике мы будем использовать готовые формулы.

Характеристическое уравнение имеет два различных действительных корня

Если характеристическое уравнение имеет два различных действительных корня , (т.е., если дискриминант ), то общее решение однородного уравнения выглядит так:
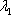
, где – константы.

В случае если один из корней равен нулю, решение очевидным образом упрощается; пусть, например, , тогда общее решение: .

Решить дифференциальное уравнение

Решение: составим и решим характеристическое уравнение:

,
Получены два различных действительных корня (от греха подальше лучше сразу же выполнить проверку, подставив корни в уравнение).
Всё, что осталось сделать – записать ответ, руководствуясь формулой

Ответ: общее решение:

Не будет ошибкой, если записать общее решение наоборот: , но хорошим стилем считается располагать коэффициенты по возрастанию, сначала –2, потом 1.

Придавая константам различные значения, можно получить бесконечно много частных решений.

Теперь неплохо бы освежить базовые понятия урока Дифференциальные уравнения. Примеры решений. А что значит вообще решить дифференциальное уравнение?Решить дифференциальное уравнение – это значит найти множество решений, которое удовлетворяет данному уравнению. Такое множество решений, напоминаю, называется общим интегралом или общим решением дифференциального уравнения.

Таким образом, в рассмотренном примере найденное общее решение должно удовлетворять исходному уравнению . Точно так же, как и диффура 1-го порядка, в большинстве случаев легко выполнить проверку:

Берем наш ответ и находим производную:

Находим вторую производную:

Подставляем , и в левую часть уравнения :

Получена правая часть исходного уравнения (ноль), значит, общее решение найдено правильно (оно, как проверено, удовлетворяет уравнению ).

Найти общее решение дифференциального уравнения, выполнить проверку

Это пример для самостоятельного решения, полное решение и ответ в конце урока.

На самом деле проверка таких простейших примеров практически никогда не выполняется, но, дело в том, что навык и сама техника проверки очень пригодятся, когда вы будете решать более сложные неоднородные уравнения второго порядка. Поэтому было целесообразно сразу же ознакомить вас с алгоритмом.

Характеристическое уравнение имеет два кратных действительных корня

Если характеристическое уравнение имеет два кратных (совпавших) действительных корня (дискриминант ), то общее решение однородного уравнения принимает вид:
, где – константы.
Вместо в формуле можно было нарисовать , корни всё равно одинаковы.

Если оба корня равны нулю , то общее решение опять же упрощается: . Кстати, является общим решением того самого примитивного уравнения , о котором я упоминал в начале урока. Почему? Составим характеристическое уравнение: – действительно, данное уравнение как раз и имеет совпавшие нулевые корни .

Решить дифференциальное уравнение

Решение: составим и решим характеристическое уравнение:

Здесь можно вычислить дискриминант, получить ноль и найти кратные корни. Но можно невозбранно применить известную школьную формулу сокращенного умножения:

(конечно, формулу нужно увидеть, это приходит с опытом решения)

Получены два кратных действительных корня

Ответ: общее решение:

Найти общее решение дифференциального уравнения

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Желающие могут потренироваться и выполнить проверку, но она здесь будет труднее.

Характеристическое уравнение имеет сопряженные комплексные корни

Для понимания третьего случая требуются элементарные знания про комплексные числа. Если материал позабылся, прочитайте урок Комплексные числа для чайников, в частности, параграф Извлечение корней из комплексных чисел.

Если характеристическое уравнение имеет сопряженные комплексные корни , (дискриминант ), то общее решение однородного уравнения принимает вид:
, где – константы.
Примечание: Сопряженные комплексные корни почти всегда записывают кратко следующим образом:

Если получаются чисто мнимые сопряженные комплексные корни: , то общее решение упрощается:

Решить однородное дифференциальное уравнение второго порядка

Решение: Составим и решим характеристическое уравнение:

– получены сопряженные комплексные корни

Ответ: общее решение:

Решить однородное дифференциальное уравнение второго порядка

Полное решение и ответ в конце урока.

Иногда в заданиях требуется найти частное решение однородного ДУ второго порядка, удовлетворяющее заданным начальным условиям, то есть, решить задачу Коши. Алгоритм решения полностью сохраняется, но в конце задачи добавляется один пункт.

Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям ,

Решение: составим и решим характеристическое уравнение:

,
Получены два различных действительных корня, поэтому общее решение:

Теперь нужно найти частное решение, соответствующее заданным начальным условиям. Наша задача состоит в том, чтобы найти ТАКИЕ значения констант , чтобы выполнялись ОБА условия.

Алгоритм нахождения частного решения следующий:

Сначала используем начальное условие :

Согласно начальному условию, получаем первое уравнение: или просто

Далее берём наше общее решение и находим производную:

Используем второе начальное условие :

Согласно второму начальному условию, получаем второе уравнение: или просто

Составим и решим систему из двух найденных уравнений:

Допустимо использовать «школьный» метод решения, но в высшей математике чаще применяют метод почленного сложения/вычитания уравнений системы, посетите соответствующий урок, если не знакомы с методом.

В составленной системе удобно разделить второе уравнение на 2 и почленно сложить уравнения:

Всё, что осталось сделать – подставить найденные значения констант в общее решение :

Ответ: частное решение:

Проверка осуществляется по следующей схеме:
Сначала проверим, выполняется ли начальное условие :
– начальное условие выполнено.

Находим первую производную от ответа:

– второе начальное условие тоже выполнено.

Находим вторую производную:

Подставим и в левую часть исходного дифференциального уравнения :
, что и требовалось проверить.

Такие образом, частное решение найдено верно.

Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям , . Выполнить проверку.

Это пример для самостоятельного решения, ответ в конце урока. Если возникли затруднения с нахождение корней характеристического уравнения, прочитайте параграфИзвлечение корней из комплексных чисел урока Комплексные числа для чайников. Если не помните значения тригонометрических функций, используйтеТригонометрические таблицы.

Как видите, особых сложностей с однородными уравнениями нет, главное, правильно решить квадратное уравнение.

Иногда встречаются нестандартные однородные уравнения, например уравнение в виде , где при второй производной есть некоторая константа , отличная от единицы (и, естественно, отличная от нуля). Алгоритм решения ничуть не меняется, следует невозмутимо составить характеристическое уравнение и найти его корни. Если характеристическое уравнение будет иметь два различных действительных корня, например: , то общее решение запишется по обычной схеме: .

В ряде случаев из-за опечатки в условии могут получиться «нехорошие» корни, что-нибудь вроде . Что делать, ответ придется записать так:

С «плохими» сопряженными комплексными корнями наподобие тоже никаких проблем, общее решение:

То есть, общее решение в любом случае существует. Потому-что любое квадратное уравнение имеет два корня.

В заключительном параграфе, как я и обещал, коротко рассмотрим:

Линейные однородные уравнения высших порядков

Всё очень и очень похоже.

Линейное однородное уравнение третьего порядка имеет следующий вид:
, где – константы.
Для данного уравнения тоже нужно составить характеристическое уравнение и уравнение и найти его корни. Характеристическое уравнение, как многие догадались, выглядит так:
, и оно в любом случае имеет ровно три корня.

Пусть, например, все корни действительны и различны: , тогда общее решение запишется следующим образом:

Если один корень действительный , а два других – сопряженные комплексные , то общее решение записываем так:

Особый случай, когда все три корня кратны (одинаковы). Рассмотрим простейшие однородное ДУ 3-го порядка с одиноким папашей: . Характеристическое уравнение имеет три совпавших нулевых корня . Общее решение записываем так:

Если характеристическое уравнение имеет, например, три кратных корня , то общее решение, соответственно, такое:

Решить однородное дифференциальное уравнение третьего порядка

Решение: Составим и решим характеристическое уравнение:

, – получен один действительный корень и два сопряженных комплексных корня.

Ответ: общее решение

Аналогично можно рассмотреть линейное однородное уравнение четвертого порядка с постоянными коэффициентами: , где – константы.

Соответствующее характеристическое уравнение всегда имеетровно четыре корня.

Общее решение записывается точно по таким же принципам, как и для однородных диффуров младших порядков. Единственное, хотелось прокомментировать тот случай, когда все 4 корня являются кратными. Пусть, например, характеристическое уравнение имеет четыре одинаковых корня . Тогда общее решение записывается так:
.

Тривиальное уравнение имеет общее решение:

Решить однородное дифференциальное уравнение четвертого порядка

Это пример для самостоятельного решения, полное решение и ответ в конце урока.

Полагаю, практически все смогут расправиться и с однородными дифференциальными уравнениями 5-го, 6-го и высших порядков. Мне очень не хотелось записывать общие формулы, рассказывать о фундаментальной системе решений и т.д. Но, процесс конструирования общего решения вроде раскрыт мной неплохо.

На посошок предлагаю решить однородный диффур как раз для закрепления вашего понимания. Да чего мелочиться:

Решить однородное дифференциальное уравнение шестого порядка

Полное решение и ответ ближе к подвалу. Караул устал – караул упал.

После такой основательной подготовки можно смело переходить к освоению линейных неоднородных уравнений второго и высших порядков.

Решения и ответы:

Пример 2: Решение: Составим и решим характеристическое уравнение:

, – различные действительные корни
Ответ: общее решение:
Проверка: Найдем производную:

Найдем вторую производную:

Подставим и в левую часть исходного уравнения :
, таким образом, общее решение найдено правильно.

Пример 4: Решение: составим и решим характеристическое уравнение:

Получены два кратных действительных корня
Ответ: общее решение:

Пример 6: Решение: Составим и решим характеристическое уравнение:

– сопряженные комплексные корни

Решения дифференциальных уравнений второго порядка

Задача 2. Решить задачу Коши

Посмотреть решение (pdf, 39 Кб)

Задача 15. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами

Посмотреть решение (pdf, 43 Кб)

Задача 16. Решить задачу Коши для дифференциального уравнения второго порядка с постоянными коэффициентами методом вариации:

Посмотреть решение (pdf, 57 Кб)

Решения задач на составление дифференциальных уравнений

Задача 11. Скорость остывания нагретого тела пропорциональна разности температур тела и окружающей среды. За 10 минут тело охладилось от 100 до 60 градусов. Температура среды постоянна и равна 20 градусам. Когда тело остынет до 25 градусов?

Посмотреть решение (pdf, 49 Кб)

Задача 12. Моторная лодка движется в спокойной воде со скоростью 5 м/сек. На полном ходу ее мотор выключается и через 40 сек после этого скорость лодки уменьшается до 2 м/сек. Определить скорость лодки через 2 минуты после остановки мотора, считая, что сопротивление воды пропорционально скорости движения лодки.

Посмотреть решение (pdf, 50 Кб)

Решения нелинейных дифференциальных уравнений

Задача 13. Решить дифференциальное уравнение

Посмотреть решение (pdf, 35 Кб)

Задача 14. Решить дифференциальное уравнение

Дифференциальные уравнения высших порядков

Дифференциальные уравнения высших порядков, решаемые в квадратурах

Уравнения, содержащие переменную и старшую производную

Разрешенные относительно старшей производной

Рассмотрим дифференциальное уравнение следующего вида:
.
Интегрируем n раз.
;
;
и так далее. Так же можно использовать формулу:
.
См. Дифференциальные уравнения, решающиеся непосредственным интегрированием

Разрешенные относительно переменной

Рассмотрим дифференциальное уравнение, в котором независимая переменная x является функцией от старшей производной:
.
Это уравнение можно решить параметрическим методом. Для этого вводим параметр . В результате получаем:
;
.
Из последнего уравнения . Интегрируя, получаем зависимость производной от x в параметрическом виде:
.
Продолжая интегрирование аналогичным образом, получим зависимость y от x в параметрическом виде.

Общий случай

Рассмотрим дифференциальное уравнение, содержащее только независимую переменную и старшую производную общего вида:
.
Его можно решить в квадратурах в параметрическом виде, если удастся подобрать такие функции и , для которых .

Если такие функции найдены, то положим . Тогда исходное уравнение выполняется автоматически. Дифференцируя первую функцию, находим связь между дифференциалами переменных x и t : . Тогда
.
Интегрируя последнее соотношение, получаем решение для производной более низкого порядка в параметрическом виде. Продолжая действовать подобным способом, получим общее решение в квадратурах.

Уравнения, содержащие только производные порядков n и n-1

Рассмотрим дифференциальное уравнение, содержащее только производные n-го и n-1-го порядков:
.
Его можно решить в квадратурах, если удастся найти такие функции и , которые удовлетворяют уравнению
.
Тогда положим
.
Считаем, что такое параметрическое представление эквивалентно исходному уравнению .

Тогда
;
.
Интегрируя эти уравнения, получим параметрическое представление производной порядка n – 2 . Продолжая подобным образом, получаем выражения остальных производных и самой функции y через параметр t .
Подробнее, см. здесь.

Уравнения, содержащие только производные порядков n и n-2

Рассмотрим дифференциальное уравнение, содержащее только производные n-го и n-2-го порядков:
.
Его можно решить в квадратурах, если удастся найти такие функции и , которые удовлетворяют уравнению
.
Положим
.
Считаем, что такое параметрическое представление эквивалентно исходному уравнению.

Тогда
;
;
;
;
.
Интегрируя, получим параметрическое представление производных порядка n, n – 1 и n – 2 . Далее интегрируем как в предыдущем случае ⇑. В результате получаем выражения остальных производных и самой функции y через параметр t .
Подробнее, см. здесь.

Дифференциальные уравнения высших порядков, допускающие понижение порядка

Уравнения, не содержащие зависимую переменную y в явном виде

Подстановка приводит к понижению порядка уравнения на единицу. Здесь – функция от .
См. Дифференциальные уравнения высших порядков, не содержащие функцию в явном виде

Уравнения, не содержащие независимую переменную x в явном виде

Для решения этого уравнения, делаем подстановку
.
Считаем, что является функцией от . Тогда
.
Аналогично для остальных производных. В результате порядок уравнения понижается на единицу.
См. Дифференциальные уравнения высших порядков, не содержащие переменную в явном виде

Однородные дифференциальные уравнения высших порядков

Уравнения, однородные относительно функции и ее производных

Дифференциальное уравнение

является однородным относительно функции и ее производных, если оно обладает свойством:
.
Здесь t – число или любая функция; число p называют показателем однородности.

Чтобы распознать такое уравнение, нужно сделать замену
.
Если после преобразований t сократится, то это однородное уравнение.

Для его решения делаем подстановку
,
где – функция от . Тогда
.
Аналогично преобразуем производные и т.д. В результате порядок уравнения понижается на единицу.
См. Однородные относительно функции и ее производных дифференциальные уравнения высших порядков

Обобщенно однородные уравнения относительно переменных

Теперь рассмотрим дифференциальные уравнения, которые не меняют вида, если сделать замену переменных: , где c – постоянная; s – измерение однородности для переменной y. При такой замене производная порядка m умножается на :
.
Если записать исходное уравнение в общем виде:
,
то оно является обобщенно однородным относительно переменных, если обладает свойством:
,
где t – число или любая функция; p – показатель однородности.

При подобные уравнения можно назвать однородными дифференциальными уравнениями относительно переменных.

Порядок такого уравнения можно понизить на единицу, если искать решение в параметрическом виде, и перейти от зависимой переменной (функции) y к новой зависимой переменной (новой функции) с помощью подстановок:
, где t – параметр.
В результате для функции получим дифференциальное уравнение n — го порядка, которое не содержит переменную t в явном виде. Далее понижаем порядок изложенным выше методом ⇑.
См. Обобщенно однородные дифференциальные уравнения относительно переменных высших порядков

Дифференциальные уравнения с полной производной

Это уравнения, которые можно привести к полной производной:
.
Отсюда сразу получаем первый интеграл:
.
Он представляет собой дифференциальное уравнение, на единицу меньшего порядка по сравнению с исходным уравнением .

В качестве примера рассмотрим дифференциальное уравнение второго порядка:
.
Разделим его на . Тогда
.
Отсюда получаем первый интеграл, который является дифференциальным уравнением первого порядка:
.
См. Дифференциальные уравнения высших порядков с полной производной.

Линейные дифференциальные уравнения высших порядков

Рассмотрим линейное однородное дифференциальное уравнение n-го порядка:
(1) ,
где – функции от независимой переменной . Пусть есть n линейно независимых решений этого уравнения. Тогда общее решение уравнения (1) имеет вид:
(2) ,
где – произвольные постоянные. Сами функции образуют фундаментальную систему решений.
Фундаментальная система решений линейного однородного уравнения n-го порядка – это n линейно независимых решений этого уравнения.

Рассмотрим линейное неоднородное дифференциальное уравнение n-го порядка:
.
Пусть есть частное (любое) решение этого уравнения. Тогда общее решение имеет вид:
,
где – общее решение однородного уравнения (1).

Линейные дифференциальные уравнения с постоянными коэффициентами и приводящиеся к ним

Линейные однородные уравнения с постоянными коэффициентами

Это уравнения вида:
(3) .
Здесь – действительные числа. Чтобы найти общее решение этого уравнения, нам нужно найти n линейно независимых решений , которые образуют фундаментальную систему решений. Тогда общее решение определяется по формуле (2):
(2) .

Ищем решение в виде . Получаем характеристическое уравнение:
(4) .

Если это уравнение имеет различные корни , то фундаментальная система решений имеет вид:
.

Если имеется комплексный корень
,
то существует и комплексно сопряженный корень . Этим двум корням соответствуют решения и , которые включаем в фундаментальную систему вместо комплексных решений и .

Кратным корням кратности соответствуют линейно независимых решений: .

Кратным комплексным корням кратности и их комплексно сопряженным значениям соответствуют линейно независимых решений:
.

Линейные неоднородные уравнения со специальной неоднородной частью

Рассмотрим уравнение вида
,
где – многочлены степеней s 1 и s 2 ; – постоянные.

Сначала мы ищем общее решение однородного уравнения (3). Если характеристическое уравнение (4) не содержит корень , то ищем частное решение в виде:
,
где
;
;
s – наибольшее из s 1 и s 2 .

Если характеристическое уравнение (4) имеет корень кратности , то ищем частное решение в виде:
.

После этого получаем общее решение:
.

Линейные неоднородные уравнения с постоянными коэффициентами

Здесь возможны три способа решения.

1) Метод Бернулли.
Сначала находим любое, отличное от нуля, решение однородного уравнения
.
Затем делаем подстановку
,
где – функция от переменной x . Получаем дифференциальное уравнение для u , которое содержит только производные от u по x . Выполняя подстановку , получаем уравнение n – 1 — го порядка.

2) Метод линейной подстановки.
Сделаем подстановку
,
где – один из корней характеристического уравнения (4). В результате получим линейное неоднородное уравнение с постоянными коэффициентами порядка . Последовательно применяя такую подстановку, приведем исходное уравнение к уравнению первого порядка.

3) Метод вариации постоянных Лагранжа.
В этом методе мы сначала решаем однородное уравнение (3). Его решение имеет вид:
(2) .
Далее мы считаем, что постоянные являются функциями от переменной x . Тогда решение исходного уравнения имеет вид:
,
где – неизвестные функции. Подставляя в исходное уравнение и накладывая на некоторые ограничения, получаем уравнения, из которых можно найти вид функций .

Уравнение Эйлера

Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
.
Однако, для решения уравнения Эйлера, делать такую подстановку нет необходимости. Можно сразу искать решение однородного уравнения в виде
.
В результате получим такие же правила, как и для уравнения с постоянными коэффициентами, в которых вместо переменной нужно подставить .

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 13-06-2017 Изменено: 11-05-2021