Системы дифференциальных уравнений с примерами решения и образцами выполнения
Также как и обыкновенные дифференциальные уравнения, системы дифференциальных уравнений применяются для описания многих процессов реальной действительности. В частности, к ним относятся различного рода физические и химические процессы, процессы нефте- и газодобычи, геологии, экономики и т.д. Действительно, если некоторые физические величины (перемещение тела, пластовое давление жидкости в фиксированной точке с тремя координатами, концентрация веществ, объемы продаж продуктов) оказываются меняющимися со временем под воздействием тех или иных факторов, то, как правило, закон их изменения по времени описывается именно системой дифференциальных уравнений, т.е. системой, связывающей исходные переменные как функции времени и производные этих функций. Независимой переменной в системе дифференциальных уравнений может выступать не только время, но и другие физические величины: координата, цена продукта и т.д.
Решение систем дифференциальных уравнений
К системе дифференциальных уравнений приводит уже простейшая задача динамики точки: даны силы, действующие на материальную точку; найти закон движения, т. е. найти функции 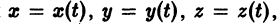
Здесь x, у, z — координаты движущейся точки, t — время, f, g, h — известные функции своих аргументов.
Система вида (1) называется канонической. Обращаясь к общему случаю системы т дифференциальных уравнений с т неизвестными функциями 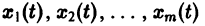
разрешенную относительно старших производных. Система уравнений первого порядка, разрешенных относительно производных от искомых функций,
Если 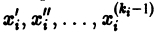
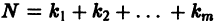
Например, одно уравнение
является мастным случаем канонической системы. Положив 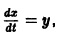
В результате получаем нормальную систему уравнений
эквивалентную исходному уравнению.
Определение:
Решением нормальной системы (3) на интервале (а, Ь) изменения аргумента t называется всякая система n функций
дифференцируемых на интервале а
Теорема:
Существования и единственности решения задачи Коши. Пусть имеем нормальную систему дифференциальных уравнений
и пусть функции 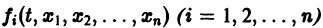
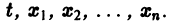

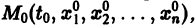

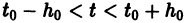
Определение:
Система n функций
зависящих от t и n произвольных постоянных 

1) при любых допустимых значениях 
2) в области 
Решения, получающиеся из общего при конкретных значениях постоянных 
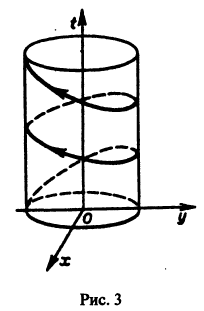
Обратимся для наглядности к нормальной системе двух уравнений,
Будем рассматривать систему значений t, x1, х2 как прямоугольные декартовы координаты точки трехмерного пространства, отнесенного к системе координат 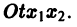
системы (7), принимающее при 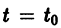
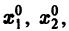
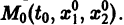
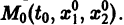
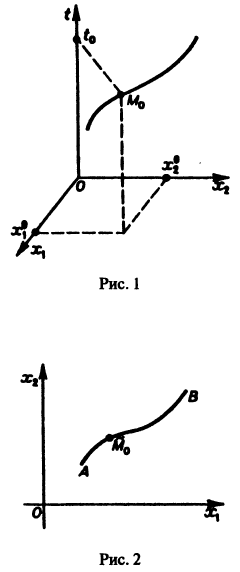
Нормальной системе (7) и ее решению можно придать еще такое истолкование: будем независимую переменную t рассматривать как параметр, а решение
системы — как параметрические уравнения кривой на плоскости 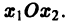
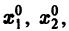
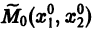
Методы интегрирования систем дифференциальных уравнений
Метод исключения
Один из методов интегрирования — метод исключения. Частным случаем канонической системы является одно уравнение n-го порядка, разрешенное относительно старшей производной
Введя новые функции 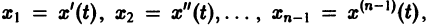
т. е. одно уравнение n-го порядка эквивалентно нормальной системе (1)
Можно утверждать и обратное, что, вообще говоря, нормальная система п уравнений первого порядка эквивалентна одному уравнению порядка n. На этом и основан метод исключения для интегрирования систем дифференциальных уравнений.
Делается это так. Пусть имеем нормальную систему
Продифференцируем первое из уравнений (2) по t. Имеем
Заменяя в правой части производные 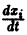
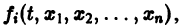
Уравнение (3) снова дифференцируем по t. Принимая во внимание систему (2), получим
Продолжая этот процесс, найдем
Предположим, что определитель
(якобиан системы функций 
Тогда система уравнений, составленная из первого уравнения системы (2) и уравнений
будет разрешима относительно неизвестных 

Внося найденные выражения в уравнение
получим одно уравнение n-го порядка
Из самого способа его построения следует, что если 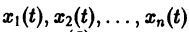
Обратно, пусть Х1(t) — решение уравнения (5). Дифференцируя это решение по t, вычислим 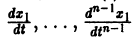
от t в систему уравнений
По предположению эту систему можно разрешить относительно 

Можно показать, что так построенная система функций
составляет решение системы дифференциальных уравнений (2). Пример:
Требуется проинтегрировать систему
Дифференцируя первое уравнение системы, имеем
откуда, используя второе уравнение, получаем
— линейное дифференциальное уравнение второго порядка с постоянными коэффициентами с одной неизвестной функцией. Его общее решение имеет вид
В силу первого уравнения системы находим функцию
Найденные функции x(t), y(t), как легко проверить, при любых значениях С1 и С2 удовлетворяют заданной системе.
Функции x(t), y(t) можно представить в виде
откуда видно, что интегральные кривые системы (6) — винтовые линии с шагом 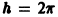
Исключая в формулах (7) параметр t, получаем уравнение
так что фазовые траектории данной системы суть окружности с центром в начале координат — проекции винтовых линий на плоскость хОу.
При А = 0 фазовая траектория состоит из одной точки х = 0, у = 0, называемой точкой покоя системы.
Замечание:
Может оказаться, что функции 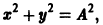
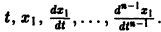
нельзя заменить эквивалентным уравнением второго порядка относительно х1 или x2. Эта система составлена из пары уравнений 1-го порядка, каждое из которых интегрируется независимо, что дает
Метод интегрируемых комбинаций
Интегрирование нормальных систем дифференциальных уравнений
иногда осуществляется методом интегрируемых комбинаций.
Интегрируемой комбинацией называется дифференциальное уравнение, являющееся следствием уравнений (8), но уже легко интегрирующееся.
Пример:
Складывая почленно данные уравнения, находим одну интегрируемую комбинацию:
Вычитая почленно из первого уравнения системы второе, получаем вторую интегрируемую комбинацию:
Мы нашли два конечных уравнения
из которых легко определяется общее решение системы:
Одна интегрируемая комбинация дает возможность получить одно уравнение
связывающее независимую переменную t и неизвестные функции 
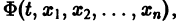
Если найдено п первых интегралов системы (8) и все они независимы, т. е. якобиан системы функций 
то задача интефирования системы (8) решена (так как из системы
определяются все неизвестные функции
Системы линейных дифференциальных уравнений
Система дифференциальных уравнений называется линейной, если она линейна относительно неизвестных функций и их производных, входящих в уравнение. Система n линейных уравнений первого порядка, записанная в нормальной форме, имеет вид
или, в матричной форме,
Теорема:
Если все функции 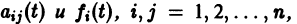
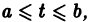
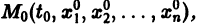
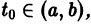
Действительно, в таком случае правые части системы (1) непрерывны по совокупности аргументов t, 
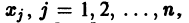
Введем линейный оператор
Тогда система (2) запишется в виде
Если матрица F — нулевая, т. е. 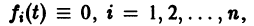
Приведем некоторые теоремы, устанавливающие свойства решений линейных систем.
Теорема:
Если X(t) является решением линейной однородной системы
то cX(t), где с — произвольная постоянная, является решением той же системы.
Теорема:
двух решений 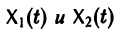
Следствие:
с произвольными постоянными коэффициентами сi решений 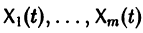
является решением той же системы.
Теорема:
Если 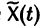
a Xo(t) — решение соответствующей однородной системы
будет решением неоднородной системы
Действительно, по условию,
Пользуясь свойством аддитивности оператора 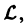
Это означает, что сумма 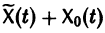
Определение:
называются линейно зависимыми на интервале a
при 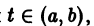

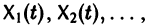
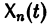
Заметим, что одно векторное тождество (5) эквивалентно n тождествам:
называется определителем Вронского системы векторов
Определение:
Пусть имеем линейную однородную систему
где 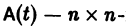
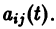
линейной однородной системы (6), линейно независимых на интервале а
с непрерывными на отрезке 
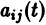
(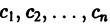
Пример:
имеет, как нетрудно проверить, решения
Эти решения линейно независимы, так как определитель Вронского отличен от нуля:
Общее решение системы имеет вид
(с1, с2 — произвольные постоянные).
Фундаментальная матрица
Квадратная матрица
столбцами которой являются линейно независимые решения 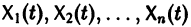
Если Х(t) — фундаментальная матрица системы (6), то общее решение системы можно представить в виде
— постоянная матрица-столбец с произвольными элементами. Полагая в (7) t = t0, имеем
Матрица 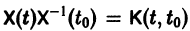
Теорема:
О структуре общего решения линейной неоднородной системы дифференциальных уравнений. Общее решение в области 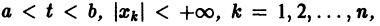
с непрерывными на отрезке 
соответствующей однородной системы и какого-нибудь частного решения 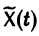
Метод вариации постоянных
Если известно общее решение линейной однородной системы (6), то частное решение неоднородной системы можно находить методом вариации постоянных (метод Лагранжа).
есть общее решение однородной системы (6), тогда
причем решения Xk(t) линейно независимы.
Будем искать частное решение неоднородной системы
где 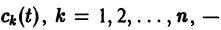
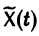
Подставляя 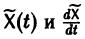
то для определения 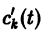
или, в развернутом виде,
Система (10) есть линейная алгебраическая система относительно 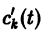
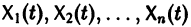
где 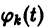
Подставляя эти значения 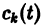
(здесь под символом 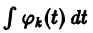
Системы линейных дифференциальных уравнений с постоянными коэффициентами
Рассмотрим линейную систему дифференциальных уравнений
в которой все коэффициенты 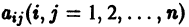
Мы рассмотрим еще метод Эйлера интегрирования линейных однородных систем дифференциальных уравнений с постоянными коэффициентами. Он состоит в следующем.
Метод Эйлера
Будем искать решение системы
где 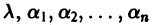
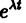
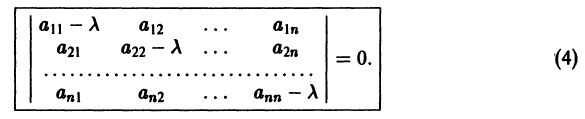
Для того, чтобы эта система (3) линейных однородных алгебраических уравнений с n неизвестными 
Уравнение (4) называется характеристическим. В его левой части стоит многочлен относительно 


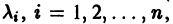
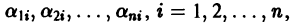
где второй индекс указывает номер решения, а первый — номер неизвестной функции. Построенные таким образом п частных решений линейной однородной системы (1)
образуют, как можно проверить, фундаментальную систему решений этой системы.
Следовательно, общее решение однородной системы дифференциальных уравнений (1) имеет вид
где 
Случай, когда характеристическое уравнение имеет кратные корни, мы рассматривать не будем.
Пример:
Ищем решение в виде
имеет корни
Система (3) для определения a1, а2 выглядит так:
Подставляя в (*) 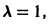
откуда а21 = а11. Следовательно,
Полагая в 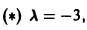
Общее решение данной системы:
Матричный метод
Изложим еще матричный метод интегрирования однородной системы (1). Запишем систему (1) в виде

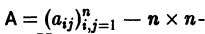
Напомним некоторые понятия из линейной алгебры. Вектор 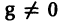
Число 
где I — единичная матрица.
Будем предполагать, что все собственные значения 
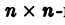
Столбцами матрицы Т являются координаты собственных векторов g1, g2 …, gn матрицы А.
Введем еще следующие понятия. Пусть В(t) — 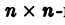








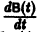
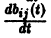
Пусть B(t) — n х n-матрица,
— вектор-столбец. Учитывая правила алгебры матриц, непосредственной проверкой убеждаемся в справедливости формулы
В частности, если В — постоянная матрица, то
так как 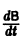
Теорема:
Если собственные значения 
где g1, g2,…, gn — собственные векторы-столбцы матрицы А, 
Введем новый неизвестный вектор-столбец Y(t) по формуле
где Т — матрица, приводящая матрицу А к диагональному виду. Подставляя X(t) из (11) в (7), получим систему
Умножая обе части последнего соотношения слева на 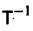
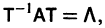
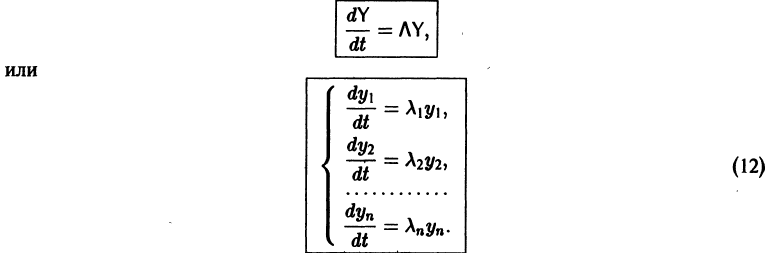
Мы получили систему из n независимых уравнений, которая без труда интегрируется:
Здесь 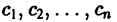
Вводя единичные n-мерные векторы-столбцы
решение Y(t) можно представить в виде
В силу (11) Х(t) = TY(t). Так как столбцы матрицы Т есть собственные векторы матрицы 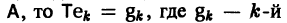
Таким образом, если матрица А системы дифференциальных уравнений (7) имеет различные собственные значения, для получения общего решения этой системы:
1) находим собственные значения 
2) находим все собственные векторы g1, g2,…, gn;
3) выписываем общее решение системы дифференциальных уравнений (7) по формуле (10).
Пример:
Матрица А системы имеет вид
1) Составляем характеристическое уравнение
Корни характеристического уравнения
2) Находим собственные векторы
Для 
откуда g11 = g12, так что
Аналогично для 
3) Пользуясь формулой (10), получаем общее решение системы дифференциальных уравнений
Корни характеристического уравнения могут быть действительными и комплексными. Так как по предположению коэффициенты 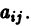
будет иметь действительные коэффициенты. Поэтому наряду с комплексным корнем 




При комплексном 
системы (7) также будет комплексным. Действительная часть
этого решения являются решениями системы (7). Собственному значению 



Пусть 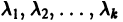
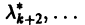
где сi — произвольные постоянные.
Пример:
1) Характеристическое уравнение системы
Его корни
2) Собственные векторы матриц
3) Решение системы
где а1, а2 — произвольные комплексные постоянные.
Найдем действительные решения системы. Пользуясь формулой Эйлера
Следовательно, всякое действительное решение системы имеет
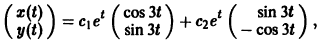
где с1, с2 — произвольные действительные числа.
Понятие о системах дифференциальных уравнений


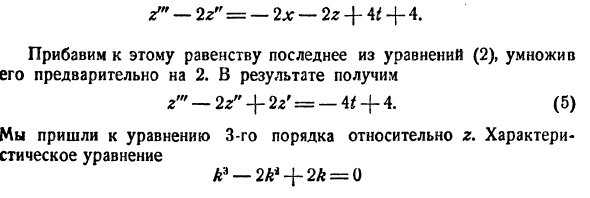

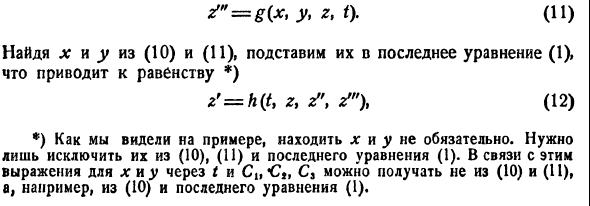

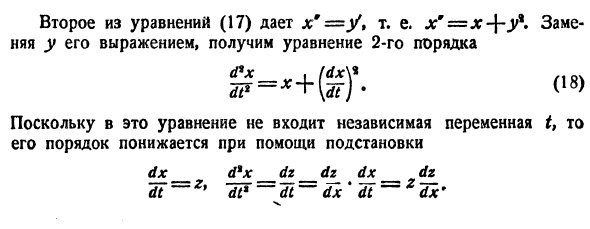


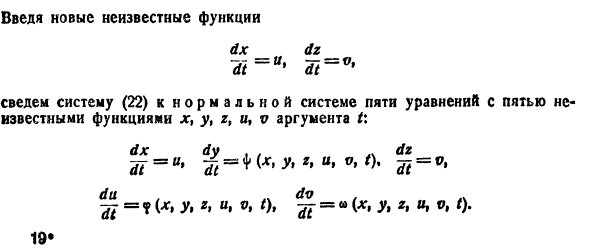
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Курсовая работа: Однородные и неоднородные системы линейных дифференциальных уравнений
| Название: Однородные и неоднородные системы линейных дифференциальных уравнений Раздел: Рефераты по математике Тип: курсовая работа Добавлен 20:31:36 25 июня 2011 Похожие работы Просмотров: 1135 Комментариев: 14 Оценило: 3 человек Средний балл: 5 Оценка: неизвестно Скачать |

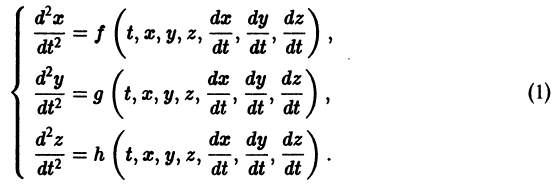
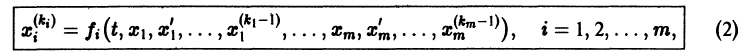
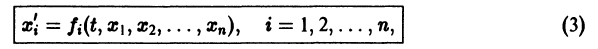
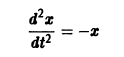
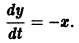
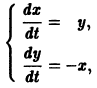
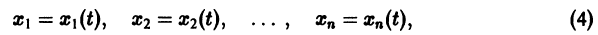
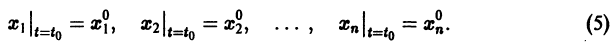
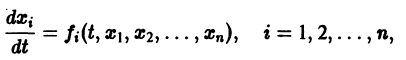
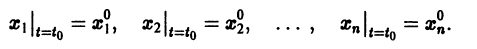
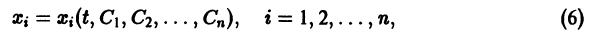

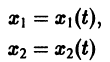
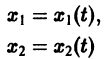
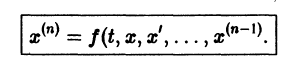
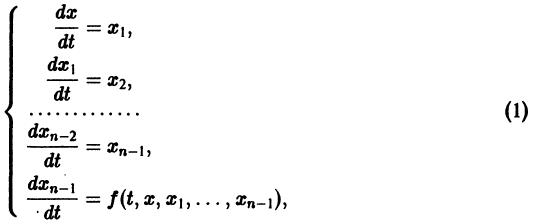
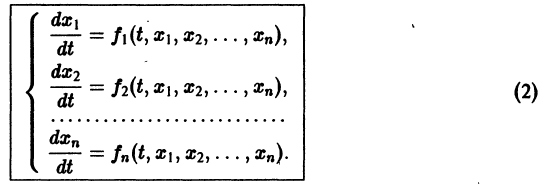
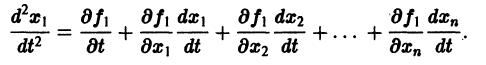
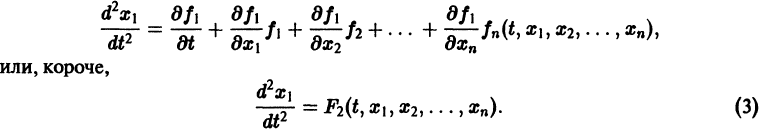
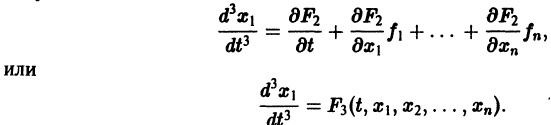
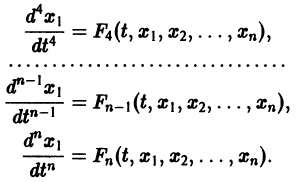
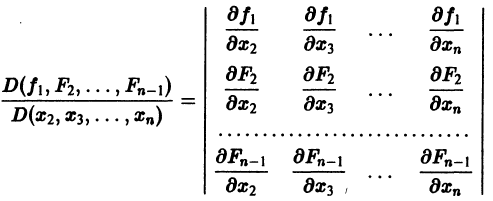
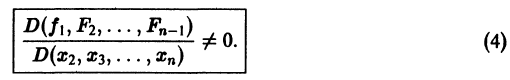
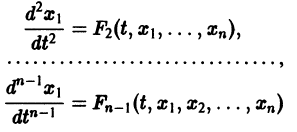
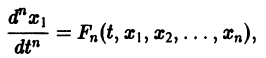
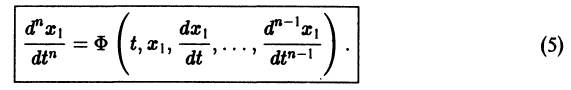
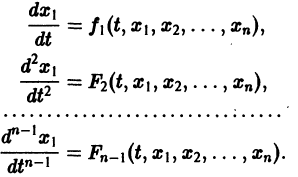
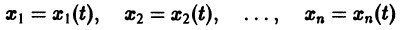

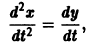
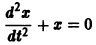
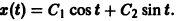

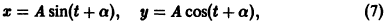
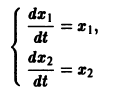
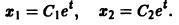
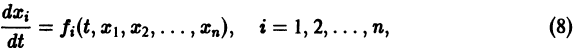
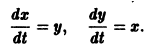


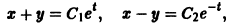
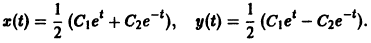
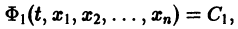
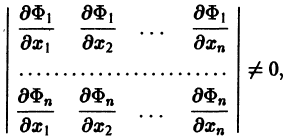
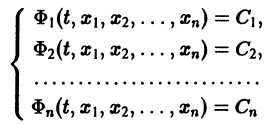
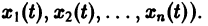
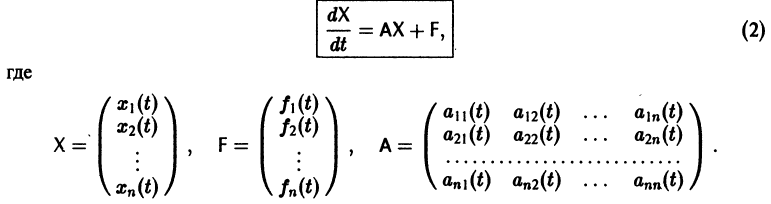
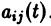
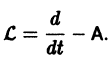
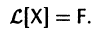

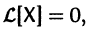
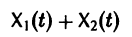
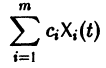
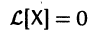
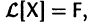

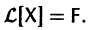
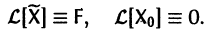
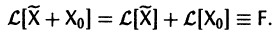
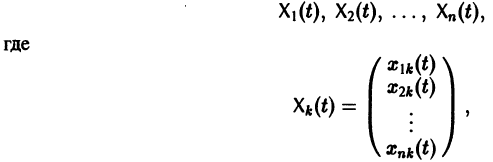
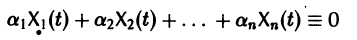
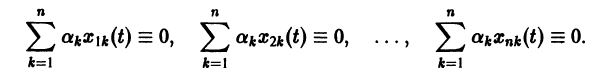
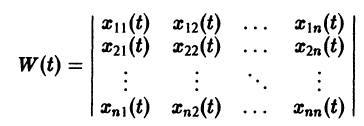

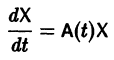
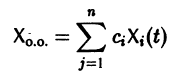
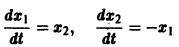
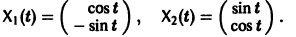
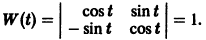
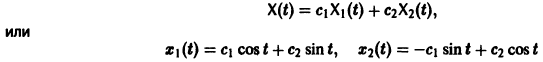
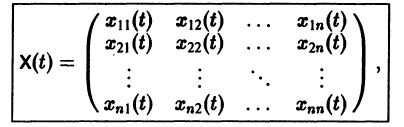
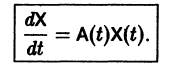
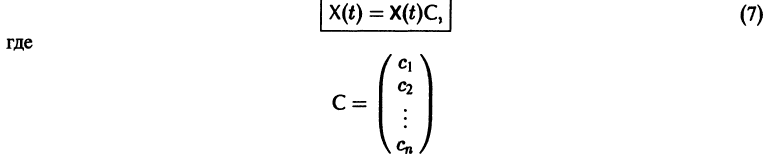
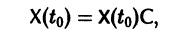
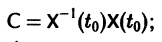
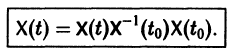
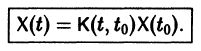

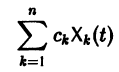
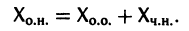
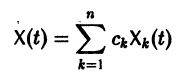
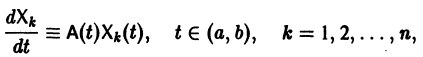
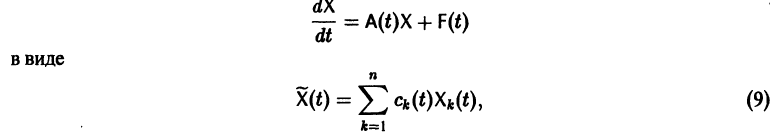
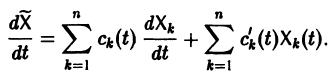
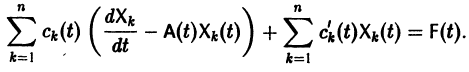
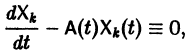
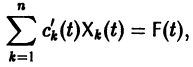
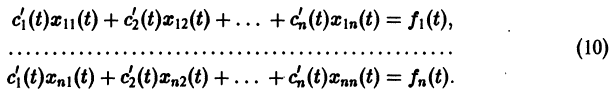
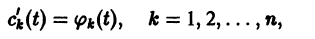
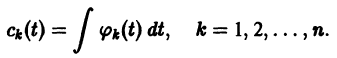
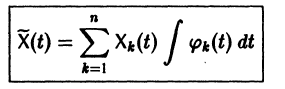
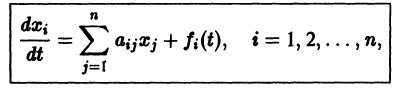
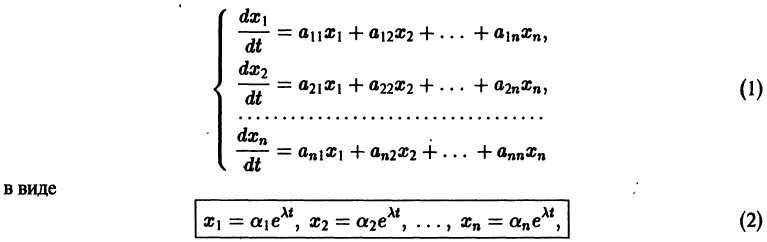
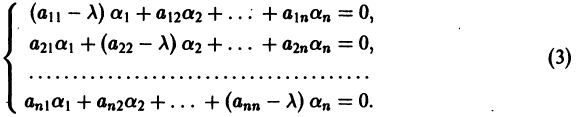

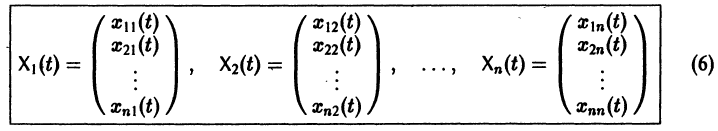
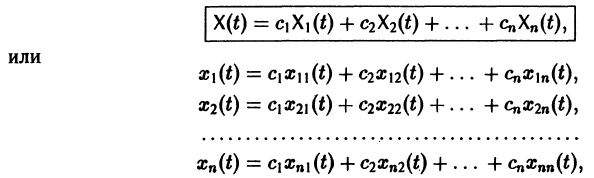
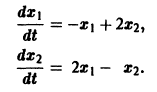
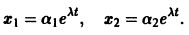

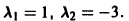

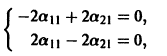
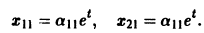
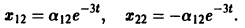
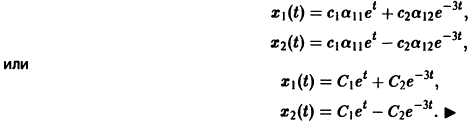

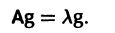
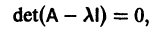
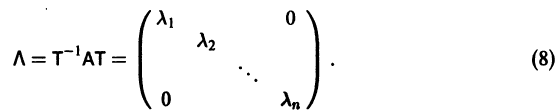
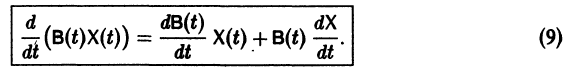
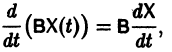
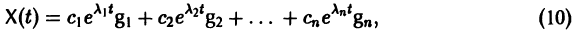

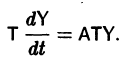
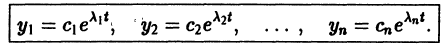
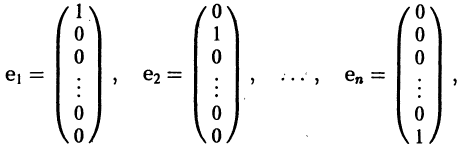
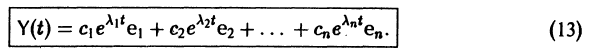
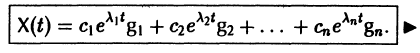
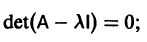
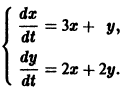
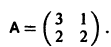

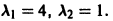
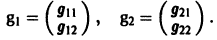
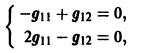
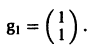
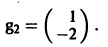
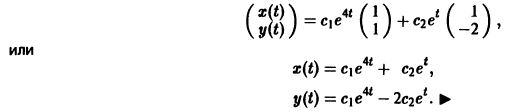
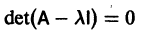
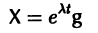
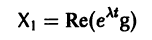
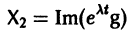
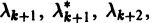
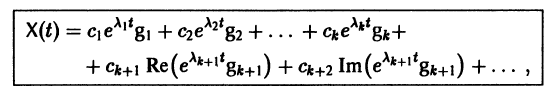
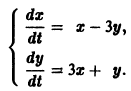
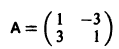

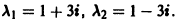
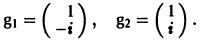
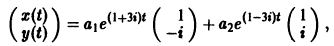
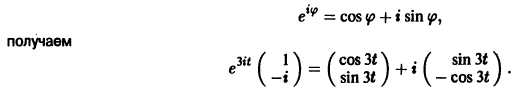
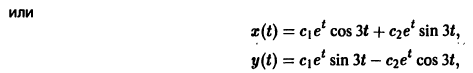

 (1)
(1)
 (2)
(2)
 (3)
(3) (4)
(4)
 (5)
(5) (6)
(6)
 .
. (7)
(7) (8)
(8)
 (9)
(9) . (10)
. (10) (11)
(11) .
.



 (14)
(14) (15)
(15)


 (16)
(16) (j = 1, 2, …,n), (17)
(j = 1, 2, …,n), (17) (j = 1, 2, …,n), (18)
(j = 1, 2, …,n), (18) (19)
(19) — действительные числа, определяемые через
— действительные числа, определяемые через  и
и  . Соответствующие комбинации функций (18) войдут в общее решение системы. [2 стр 112-115]
. Соответствующие комбинации функций (18) войдут в общее решение системы. [2 стр 112-115]


 (20)
(20) (21)
(21) .
. .
. .
.
 , (22)
, (22) (23) [3 стр 519-522]
(23) [3 стр 519-522]


 .
.


 — производные постоянные. Таким образом, решение исходной системы будет
— производные постоянные. Таким образом, решение исходной системы будет
 (24)
(24)
 и
и 
 [ 3 стр 529-531]
[ 3 стр 529-531]

 . Находим корни:
. Находим корни:

 .
. и определяем
и определяем  и
и  :
:

 . Полагая
. Полагая  , получаем
, получаем  . Таким образом, мы получили решение системы:
. Таким образом, мы получили решение системы:

 и определяем
и определяем  и
и  :
:
 и
и  =1,
=1, 



 или
или 

 и определяем
и определяем  и
и  :
: или
или  =>
=> 
 . Полагая
. Полагая  , получаем
, получаем  .
.

 и определяем
и определяем  и
и  :
:
 =1,
=1, 
















 Подставляем это значение p1 в первое уравнение и находим
Подставляем это значение p1 в первое уравнение и находим  Приняв
Приняв  получаем
получаем 
 т.е. собственный вектор (3; 1; -3).
т.е. собственный вектор (3; 1; -3).


 или
или 


 в систему (3) и определяем
в систему (3) и определяем  и
и  :
: или
или 
 . Полагая
. Полагая  .
.

 в систему (3), находим:
в систему (3), находим:
 .
.








 или
или 






 до решать
до решать











 (простой корень), ему соответствует собственный вектор
(простой корень), ему соответствует собственный вектор
 (корень кратности 2), которому соответствуют два линейно независимых собственных вектора
(корень кратности 2), которому соответствуют два линейно независимых собственных вектора





 . Собственными векторами, отвечающими найденным собственным значениям, будут соответственно
. Собственными векторами, отвечающими найденным собственным значениям, будут соответственно ,
, 





 — произвольные постоянные. Таким образом, решение исходной системы будет
— произвольные постоянные. Таким образом, решение исходной системы будет



 . Собственными векторами, отвечающими найденным собственным значениям, будут соответственно
. Собственными векторами, отвечающими найденным собственным значениям, будут соответственно ,
, 


 в исходную систему. Получим
в исходную систему. Получим


 и общего решения
и общего решения  соответствующей однородной системы, то окончательно получаем
соответствующей однородной системы, то окончательно получаем



 . Им соответствуют собственные векторы
. Им соответствуют собственные векторы ,
, 

 в исходную систему. Получим
в исходную систему. Получим



