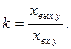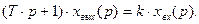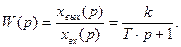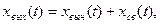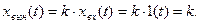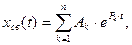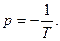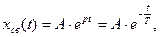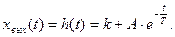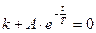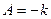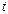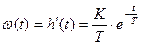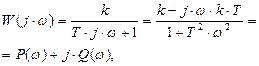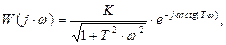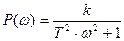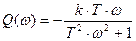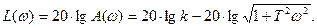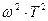Динамические свойства апериодического звена описываются уравнением

Апериодическое звено первого порядка

Апериодическим звеном первого порядка называется такое звено, выходная величина которого в функции времени изменяется по экспоненциальному закону. Апериодические звенья называют также инерционным, статическим, релаксационным, одноёмкостным и др.

Инерционное звено описывается дифференциальным уравнением первого порядка

,

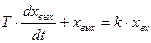
где T – постоянная времени звена (T>0);

– коэффициент передачи (усиления) звена.

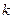
К апериодическим звеньям можно отнести: R-L и R-C цепи, генераторы постоянного тока, фильтры, термисторы, механические устройства, имеющие массу и силу трения (без пружин) и другие подобные устройства, в которых возможно накопление какого-либо вида энергии и её рассеивания.

Операторное уравнение апериодического звена

Передаточная функция звена

На структурных схемах графически инерционное звено изображается следующим образом:

Временная характеристика, представляющая реакцию звена на ступенчатое воздействие x_вх(t)=1(t), определяется зависимостью .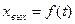

Выходная величина в переходном режиме определяется

где вынужденная составляющая выходной величины

Cвободная составляющая выходной величины x_вых(t) определяется из следующего выражения

где P_k – корни характеристического уравнения звена

т.е.

Отсюда

Начальное значение для переходной функции найдется

при t=0,

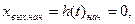
т.е.

или

Окончательно получаем следующее выражение для переходной функции:

(3.11)

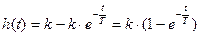
или 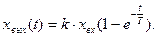(3.12)

На рис.3.5,а приведена временная характеристика, представляющая собой экспоненту. Время достижения установившегося значения

при , при .

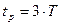
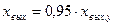
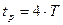
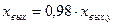
представлена на рис.3.5,б.

На структурных и функциональных схемах апериодические звенья условно изображаются следующим образом

Амплитудно-фазовая характеристика апериодического звена

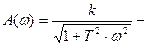
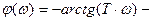
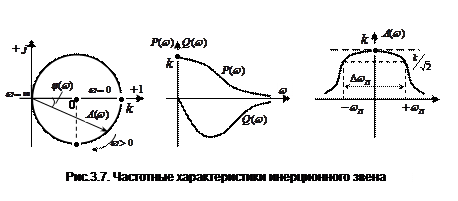
где модуль вектора W (jω);

аргумент вектора W (jω).

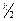
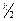
АФХ представляет собой окружность радиусом с центром в точке 0, лежащей на оси абсцисс на расстоянии от начала координат.

Уравнения вещественной и мнимой характеристик

Логарифмическая амплитудная частотная характеристика (ЛАЧХ) может быть получена путём логарифмирования выражения для A(ω).

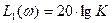
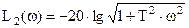
В этом выражении слагаемое представляет постоянную величину, не зависящую от частоты. Рассмотрим вторую составляющую ЛАЧХ

.

Полагая, что

Если частотные характеристики получены экспериментально, по ним нетрудно определить параметры звена T и k, пользуясь описанной выше зависимостью между этими характеристиками и передаточной функцией.

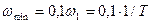
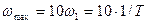
На примере этого звена явно видно, что величина полосы пропускания звеном частот, т.е. ширина частотной характеристики, является мерой быстродействия звена. Полоса пропускания частот обычно определяется диапазоном частот от , на декаду меньшей минимальной частоты сопряжения, до , на декаду большей максимальной частоты сопряжения. Чем больше этот диапазон частот, тем короче его переходная характеристика, т.е. меньше инерционность звена.

Дата добавления: 2016-03-20 ; просмотров: 10700 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

3. Частотные характеристики систем автоматического управления. ч. 3.3 Апериодическое звено 1–го порядка

3.3. Апериодическое звено 1–го порядка (инерционное звено)

Вывод свойств(характеристик) апериодического звена сделаем на примере фрагмента (части) ядерного реактора, а именно – входной камеры смешения.

Рисунок 3.3.1 Расчетная схема камеры смешения

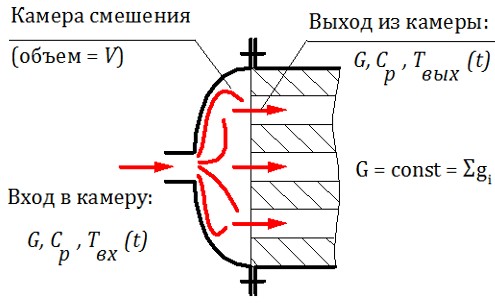
Сделаем следующие допущения:

расход теплоносителя постоянен: G = const;

теплоемкость теплоносителя = const;

входящий в камеру смешения теплоноситель полностью перемешивается в камере смешения, т.е. температура жидкости, поступающей в каждый тепловыделяющий канал, одинакова;

теплообмен камеры смешения с окружающей средой пренебрежимо мал.

Уравнение теплового баланса:

где: — плотность теплоносителя,
– удельная теплоемкость,
– объем камеры смешения, ;
– расход теплоносителя, ;
– температура теплоносителя на входе и выходе, соответственно;
– температура (перемешанного) теплоносителя в камере смешения .

Условие стационара когда левая часть уравнения равна нулю:

Введем новые переменные:

Подставляя эти соотношения в (3.3.1), получаем:

Сокращая на и , получаем:

Введем новую переменную — постоянная времени:

Таким образом получили линейное дифференциальное уравнение, причем переменные и — нормализованные, что обеспечивает равенство их нулю при t ≤ 0

– постоянная времени;
– аналог y’(t);
– аналог y(t);
– аналог x(t);

Уравнение (3.3.3) соответствует типовому апериодическому звену 1-го порядка, в котором коэффициент K = 1. В общем случае уравнение динамики апериодического звена 1-го порядка имеет вид:

Если начальные условия нулевые, то можно перевести в изображения:

Уравнение динамики в изображениях:

Уравнение динамики в изображениях:

Найдем выражение для АФЧХ:

Умножим на комплексно – сопряженное значение :

Анализируя поведение и при и при , получаем:

Подставляя в формулы (3.3.8) различные значения частоты ω, найдем соответствующие значения u(ω) и v(ω). Построим эти вектора на комплексной плоскости:

Рисунок 3.3.2 – Годограф АФЧХ апериодического звена 1-го порядка

Анализ показывает, что годограф АФЧХ — полуокружность радиусом K/2. Формулы для дейстивительной части вектора и мнимой части вектора, позволяют вычислить частоту, на которой вектор находится в нижней точке окружности (см. рис. 3.3.2).

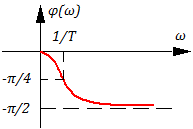
Угол сдвига фазы при данной частоте:

Найдем зависимость амплитуды от частоты:

Учитывая, что годограф АФЧХ находится в IV-ой квадранте:

Рисунок 3.3.3 – АЧХ апериодического звена 1-го порядка Рисунок 3.3.4 – ФЧХ апериодического звена 1-го порядка

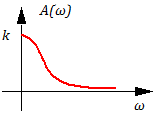
Логарифмическая амплитудная характеристика (ЛАХ) и фазочастотная характеристика (ФЧХ).

Рисунок 3.3.5 ЛАХ и ЛФЧХ апериодического звена 1-го порядка

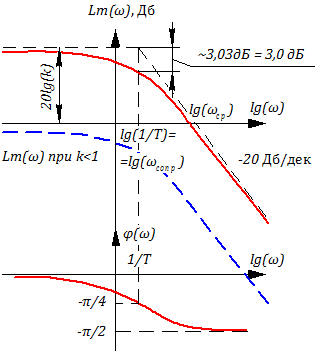
Анализируя частотные свойства данного звена, видим, что

при ω >>свойства звена приблизительно совпадают со свойствами идеального интегрирующего звена, т.е. .

при ω на свойства звена оказывают примерно равное “влияние” свойства идеального усилительного и идеального интегрирующего звена.

Принято называть частоту, при которой происходит “излом” ЛАХ

− сопрягающей частотой,

причем не трудно показать, что при ω_сопр величина амплитуды А(ω_сопр) меньше амплитуды при нулевой частоте A(0) = K в раз:

Частотой среза ω_ср называют такое значение частоты, при которой модуль (амплитуда) выходного сигнала (воздействия) равна 1.

Если >1 » alt=»K>>1 » src=»https://habrastorage.org/getpro/habr/upload_files/f05/093/192/f05093192358ee4201d57f34a0f54e60.svg»/>, то частота среза

Если , то частоты среза не существует !

Найдем переходную функцию звена (реакция на единичное ступенчатое воздействие):

Используя обратное преобразования Лапласа (см. пример в разделе 2) получим:

Тогда, дифференцируя по времени, получаем весовую функцию ω(t):

Множитель 1(t) обеспечивает равенство нулю при t ≤ 0

Рис.3.3.6 Переходная функция апериодического звена 1-го порядка Рис.3.3.7 Весовая функция апериодического звена 1-го порядка

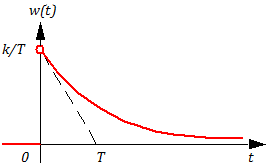
Постоянная времени Т характеризует инерционность переходных процессов в звене. Чем больше Т, тем инерционнее звено (т.е. медленнее идет переходной процесс).

Примерами апериодического звена 1- го порядка являются:

1) пассивные R−L или R−C цепочки (см. рисунок 3.3.8);

Рисунок 3.3.8 Примеры апериодических звеньев 1-го порядка

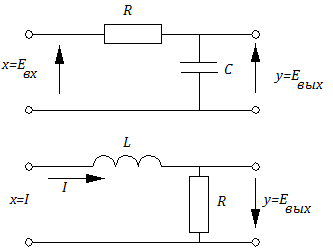
2) упрощенная модель гидротурбины, где x(t) — приводной момент; y(t) − скорость вращения ротора турбины;

3) электродвигатель (постоянного тока или асинхронный) с учетом инерционности якоря (ротора), где x(t) − напряжение в обмотке возбуждения, а y(t)− скорость вращения якоря (ротора) выходного вала;

4) тепловые датчики, например, термопара, где: x(t) –температура одного (“горячего”) спая, а y(t) – термо Э.Д.С.

5) выходная камера смешения в реакторе (приближенно)

6) различные элементы реактора, описываемые в рамках точеных моделей (например, активная зона или ядерное горючее) с использованием закона Фурье:

где: T(t) − температура топлива;

− “объемный” коэффициент теплоотдачи;

− выделяющаяся энергия;

− температура кипения теплоносителя.

Пример 1

Лично мне всегда было интересно, насколько теория совпадает с практикой, особенно для элемента ядерного реактора. Идеальный вариант – это разобрать туалетный бачок и сделать из него модель реактора, но, боюсь, домашние не одобрят, поэтому сравнивать будем с «цифровым двойником».

Рассмотрим расчет характеристик камеры смешения, в которую подается вода при температуре 20 °С и атмосферном давлении.

В качестве единичного воздействия будем считать изменение температуры на 1 °C.

Свойства воды при 20 градусах и атмосферном давлении:

теплоёмкость: = 4183 ;

плотность: = 998.2 .

объем камеры смешения: V = 0.1 ;

массовый расход воды: G = 50 .

Решим задачу в двух приближениях:

В первом случае используем стандартный блок «Инерционное звено первого порядка», который есть в любой системе структурного моделирования, и модель общего вида.

Во втором воспользуемся расчетным тепло-гидравлическим кодом НS, который используется для создания профессиональных моделей в атомной отрасли.

Параметры блока «Инерционное звено первого порядка» задаем с помощью скриптового языка при инициализации проекта, где рассчитывается постоянная времени. (см. рис. 3.3.9). В качестве входного воздействия задаем ступеньку на пятой секунде расчета величиной 0.05, что соответствует повышению на 1 °C от начальных 20 °C .

На схеме присутствует также блок «Построение частотных характеристик», обеспечивающий расчет ЛАХ и ФЧХ в заданном диапазоне 0.1 – 1000 1/с.

Расчетная схема и результаты расчета приведены на рисунке 3.3.9:

Рисунок 3.3.9 Частотный анализ модели камеры смешения в виде стандартного апериодического звена

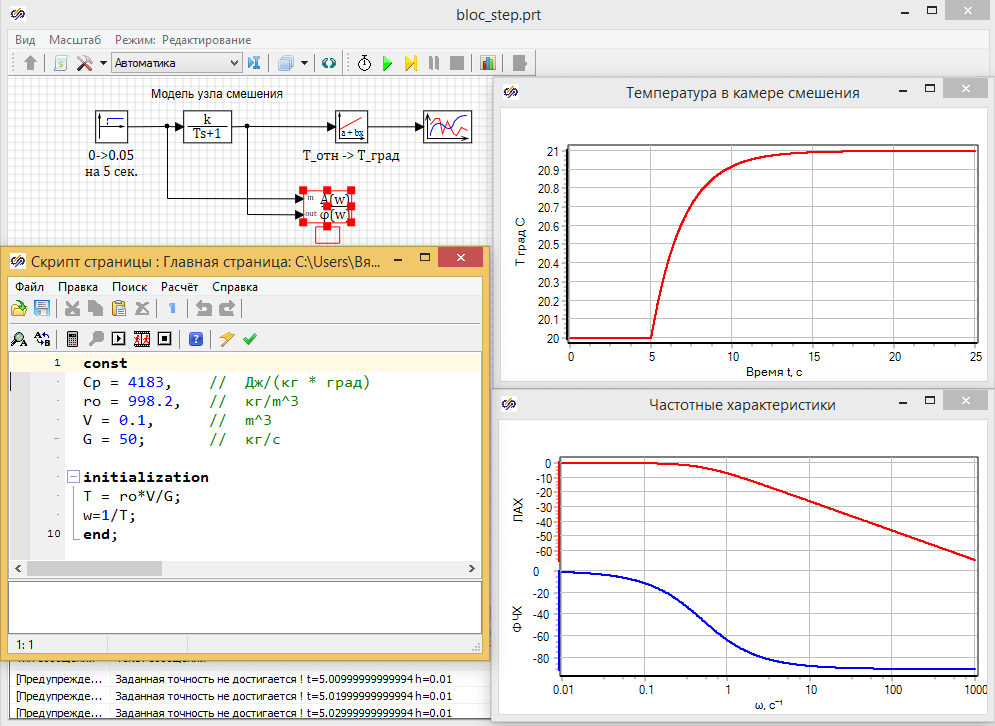
Видно, что расчетные характеристики в модели совпадают с теоретическими:

1) Постоянная времени T = 1.996

2) Сопрягающая частота w_сп = 1/T = 0,5009

Годограф звена, построенный с помощью Гармонического анализатора, представлен на рисунке 3.3.10, Видно, что получена полуокружность с центром в точке (0, 0.5) и диаметром К = 1, как и предсказано в теоретической части.

Рисунок 3.3.10 Годограф модели камеры смешения в виде «Инерционного звена первого порядка».

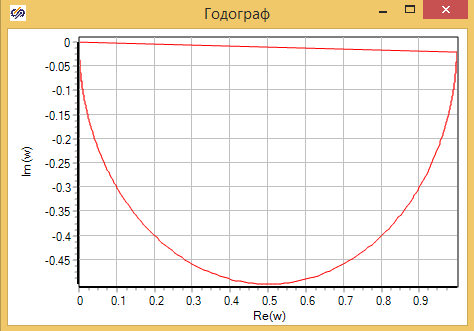
Второй вариант модели в камере смешения моделируется с помощью тепло-гидравлического расчетного кода — НS. Данный код входит в состав «Среды динамического моделирования технических систем SimTech». В коде решается более подробная система уравнений теплофизики, описание можно посмотреть здесь. Модель камеры смешения будет состоять из 4 элементов:

Блок «Подпитка» обеспечивает подачу теплоносителя с заданными параметрами и заданным расходом. В нашем случае это вода при атмосферном давлении и температурой 20 °C.

Блок «Внутренний узел» (Node_1), — модель камеры смешения.

Блок «Канал общего вида» моделирует обобщенно каналы отвода теплоносителя от камеры смешения (состоит из 10 участков).

Блок «Граничный узел» задает температуру и давление на выходе из каналов. В нашем случае – атмосферное давление и температуру.

Общий вид модели приведен на рисунке 3.3.11 Цветовая шкала показывает распределение давления в канале, который идет после камеры смешения. Исходя из уравнений физики, система рассчитывает перепад давления, соответствующий заданному расходу по каналу (50 кг/с) с учетом его геометрии, свойств жидкости, шероховатости и т.п.

Рисунок 3.3.11 Модель камеры смешения в коде НS.

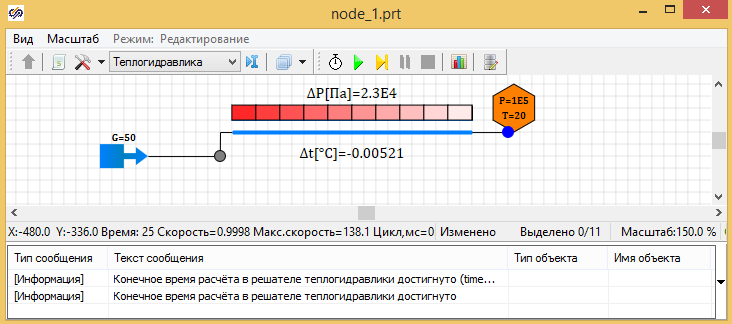
Если вывести график температуры в узле, то можно увидеть, что в начальный момент расчёта происходит какой-то переходной процесс, несмотря на то что никакого внешнего воздействие на систему нет (см. рис. 3.3.12).

Рисунок 3.3.12 Температура в узле в начальный период расчета.

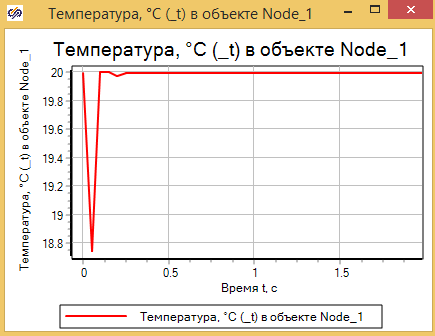
Все дело в том, что система у нас динамическая, и распределение расхода и температур по узлам модели в начале расчёта не соответствует стационарному состоянию. И некоторое время происходят колебания расходов и, соответственно, температур до достижения равновесия.

Чтобы в расчётах не учитывать данные колебания, и не заставлять пользователя задавать вручную состояние каждой точки системы, используется специальный инструмент «Файл рестарта». В этот файл сохраняются состояния системы в конце расчета или с заданным шагом. И эти состояния можно загрузить при старте системы. Если сохранить состояние системы, находящейся в стационаре один раз, то потом можно использовать его для начала расчёта, тем самым избегая колебаний системы. Для этого необходимо:

В настройках проекта задать имя файла, в который мы хотим сохранить стационарное состояние в конце расчета.

В следующих расчетах указать этот файл как начальное состояние при старте нового расчета, и изменить в нем модельное время на 0 (см. рис. 3.3.13).

Не забываем снять галочку «Сохранять рестарт при останове», если мы не хотим каждый раз получать новое состояние после каждого расчета.

Рисунок 3.3.13 Настройка файлов рестартов.

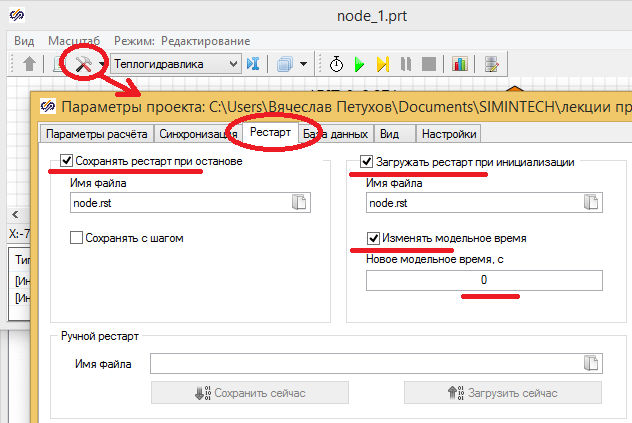
Теперь если загрузить систему из файла рестарта, созданного в стационарном состоянии, то колебания температуры на начальном этапе исчезнут. И можно проводить эксперименты с воздействием.

Для того, чтобы сравнить модель в виде динамического звена и модель в тепло-гидравлическом коде, сделаем пакет из двух проектов:

гидравлическая модель в коде НS;

модель виде одного звена.

Обмен данными будет идти через базу данных сигналов. Передадим результаты расчета из гидравлического кода в модель с одним звеном и выполним сравнение результатов. Вид пакета представлен на рисунке 6.

В главном скрипте гидравлической схемы пропишем переменную T_input – температуру на входе в камеру, на 5 секунде расчёта увеличим эту температуру на °C. А температуру в узле будем записывать в базу данных сигналов в категорию nodе_HS, переменная T_out.

В модели общего вида прочитаем значение сигнала в базе данных nodе_HS_T_out.

Сравним с выходом из апериодического звена (модель камеры смешения) и выведем на один график.

Рисунок 3.3.13 Пакет для сравнения моделей узла смешения.

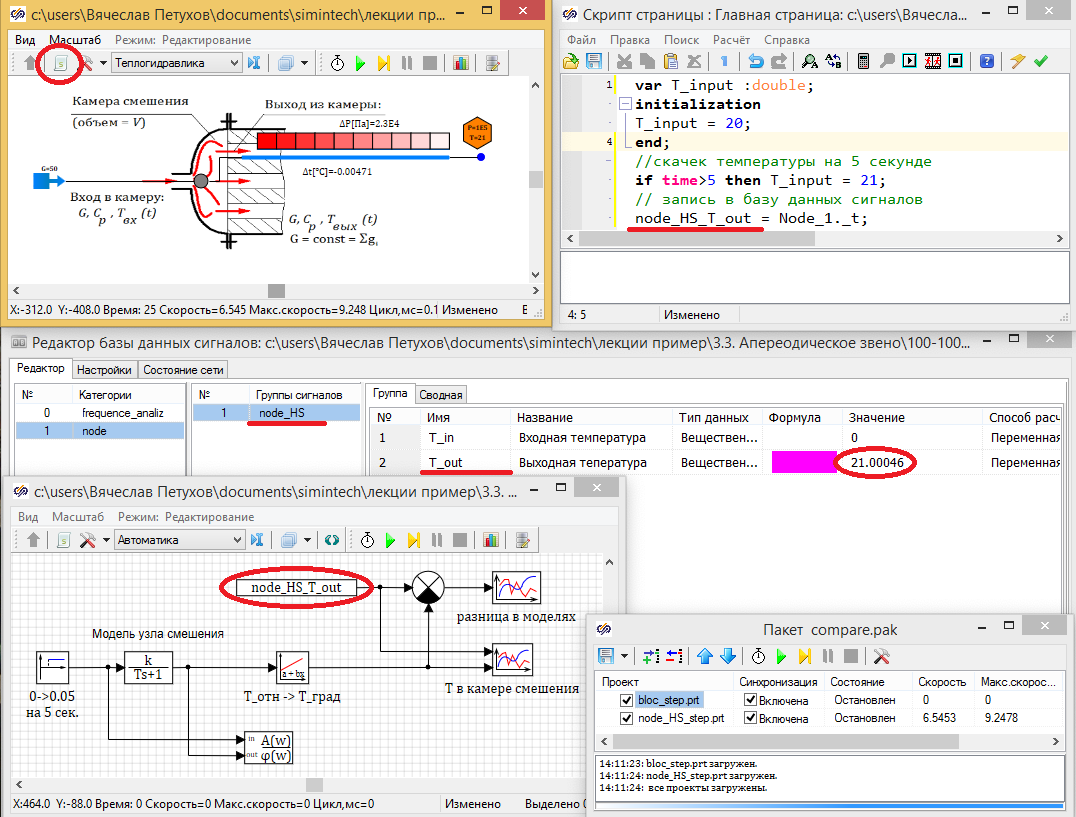
Результаты совместного расчета представлены на рисунке 3.3.14

Если на общем графике в масштабе 20 – 21 °C графики практически совпадают, то анализ графика сравнения показывает наличие расхождения в момент ступенчатого изменения температуры. Причем максимальное расхождение 0.0085 °C отмечено именно в момент переключения, а потом происходит выравнивание температуры (см. рис. 3.3.14).

Рисунок 3.3.14 Сравнение переходного процесса для разных моделей камеры смешения.

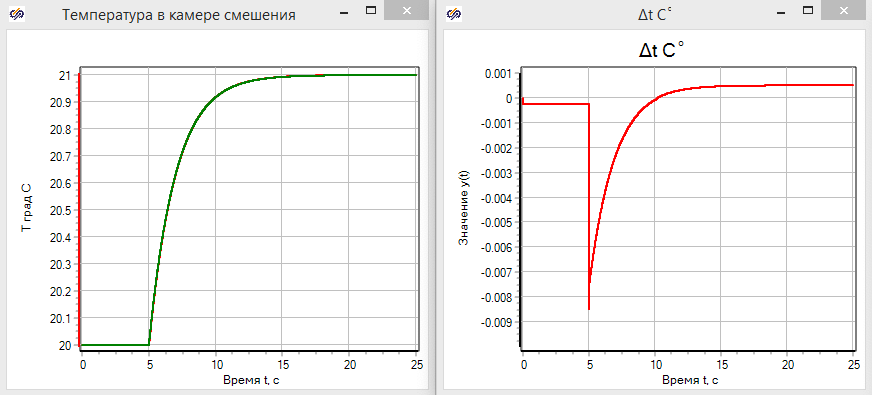
Разница связанна как раз с более сложной и детализированной моделью в тепло-гидравлическом коде НS. Дело в том, что в реальности и плотность и теплоёмкость воды не являются постоянными, а зависят от параметров давления и температуры, и даже изменение температуры на один градус ведет к изменению подведения.

Если в масштабе посмотреть на поведение давления в камере смешения и расхода из нее, мы увидим, что несмотря на то, что расход в камеру задавался постоянным, увеличение температуры скачком привело к возникновению колебательного процесса в давлении и массовом расходе из камеры (см. рис. 3.3.15).

Рисунок 3.3.15 Колебания давления и расхода при ступенчатом изменении температуры.

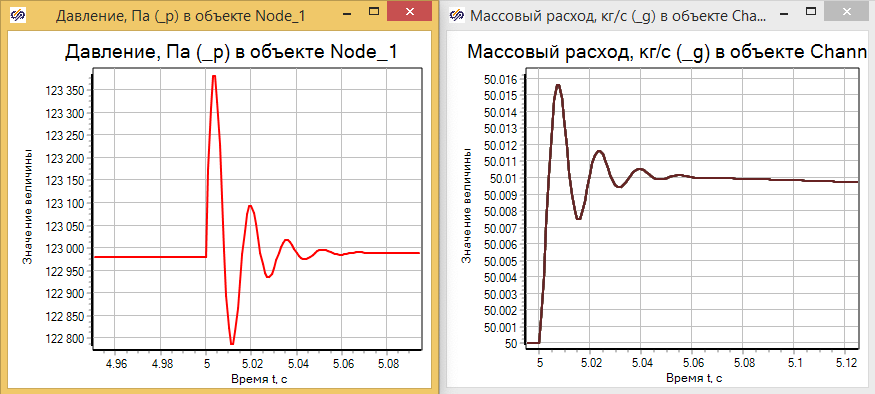
Колебания незначительны по времени и по амплитуде, но тем не менее они влияют на расчетный процесс и хорошо наблюдаемы при масштабировании графиков.

Проведем исследования с помощью блока «Гармонический анализатор«. Создадим пакет проектов, состоящий из:

тепло-гидравлической модели (см. рис. 3.3.11);

модели частотного анализа. (см. рис. 3.3.16).

Рисунок 3.3.16 Модель частотного анализа внешней системы.

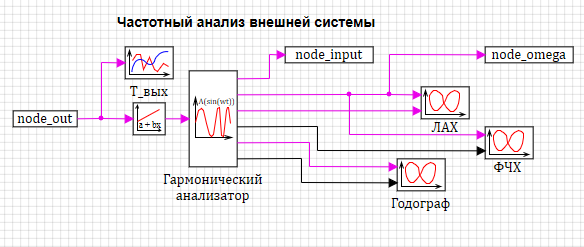
В предыдущей лекции у нас блок гармонического анализа и анализируемая модель были в одном проекте. В данном проекте блок гармонического анализа передает воздействие в базу сигналов и забирает из нее отклик – температуру в камере смешения.

Особенностью данной модели является то, что в начале расчёта на низких частотах нам нужен большой шаг интегрирования, чтобы считать медленный процессы быстрее. В начале анализа у нас частота 0.001 Гц.

А в конце процесса частота 1000 Гц, и нам нужно сократить шаг интегрирования, чтобы получить достаточное количество точек в синусоидальном сигнале при высокой частоте.

Поэтому в базу данных записывается не только тестовое воздействие, но и текущая частота (см. рис. 3.3.17). Это позволяет при увеличении частоты воздействия уменьшить минимальный шаг расчета тепло-гидравлической схемы. Скрипт модели приведен на рисунке 3.3.17.

Рисунок 3.3.17 Скрипт гидравлической модели.

Как работает этот скрипт?

Начальное значение температуры 20 °C.

Если частота воздействия больше 100, то минимальный шаг модели 0.00001, иначе (при частоте воздействия меньше 100) минимальный шаг модели 0.0001.

Температура в блоке подпитки T_input рассчитывается как сумма начальной температуры 20°C и величины воздействия node_input из базы данных сигналов, которое формирует блок гармонического анализатора в диапазоне -1 … +1 °C.

Температура в узле передаётся в базу данных для гармонического анализатора.

Результат длительного расчёта представлен на рисунке 3.3.18.

Рисунок 3.3.18. Результаты анализа частотного анализа гидравлической модели.

Мы видим, что несмотря на различия в математических моделях, частотные характеристики камеры смешения в тепло-гидравлическом коде отлично совпадают в диапазоне частот 0.001 до 50 Гц. Сравни с рисунком 3.3.9

Однако на частотах выше 70 ФЧХ ведет себя не так, как в идеальном апериодическом звене. Если открыть график давления в камере смешения и график массового расхода в канале, можно наблюдать увеличение амплитуды колебаний с ростом частоты воздействия (см. рис. 3.3.19).

Рисунок 3.3.19 Давление в узле и расход в выходном канале с ростом частоты воздействия по температуре.

Таким образом, изначальная модель, в которой можно было пренебречь колебаниями давления и массового расхода, с ростом частоты воздействий выше 50 Гц превращается в модель, где принятые допущения уже не работают.

Выводы.

Теория автоматического управления действительно работает, и даже ядерный реактор можно представить в виде набора динамических звеньев.

Однако нужно внимательно смотреть за параметрами процессов, и определять диапазоны, где принятые упрощения настолько изменяют систему, что делают модель не верной .

Пример 2

Лично для меня наиболее удивительным в теории автоматического управления является тот факт, что абсолютно разные физические процессы могут быть представлены одинаковыми типовыми звеньями САР. Для иллюстрации этого удивительного факта на рисунке 3.3.20 представлена модель эклектической схемы, которая работает как апериодическое звено.

Напряжение в электрической схеме ведет себя в динамике так же, как температура воды в камере смешения. Даже Годограф получается с тем же радиусом, разве это не чудо!

Рисунок 3.3.20. Электрическая схема и ее частотные характеристики.

Апериодическое (инерционное, статическое) звено. Передаточная функция и уравнения

Дифференциальное уравнение, описывающее взаимосвязь входного и выходного сигналов апериодического типового динамического звена (ТДЗ), можно представить в следующем виде:

Где: k – коэффициент передачи, Т₀ – постоянная времени.

Дифференциальное уравнение является не самой удобной формой представления математической модели объекта или звена. Это связано с тем, что решения любого дифференциального уравнения довольно сложная вычислительная процедура. Более удобна и, соответственно чаще используемая, математическая модель объекта, записанная в виде передаточной функции.

Передаточная функция – это преобразованное по Лапласу исходное дифференциальное уравнение, то есть уравнение, записанное в виде преобразованных по Лапласу выходного и входного сигналов объекта (звена).

Исходное дифференциальное уравнение в преобразовании Лапласа называют оригиналом, а записанное в операторной форме преобразованное уравнение – его изображением. Суть преобразования Лапласа заключается в замене на функции комплексных переменных Х_вых(р) и Х_вх(р) функций вещественных переменных Х_вых(τ) и Х_вх(τ), где р – оператор Лапласа (комплексное число р = ±m±in). Данные функции связываются между собой интегралом Лапласа:

Для большинства используемых в ТДЗ дифференциальных уравнений, чисто формальным условием перехода от оригинала к изображению будут представленные ниже замены:

Использовав приведенное выше условие довольно легко получить изображение, то есть перейти к операторной форме записи дифференциального уравнения апериодического звена.

Оригинал дифференциального уравнения апериодического звена имеет следующий вид:

Операторная форма записи (изображения) уравнения апериодического звена:

Огромным преимуществом данного преобразования является то, что записанное в операторной форме исходное дифференциальное уравнения становится алгебраическим. Но стоит отметить, что если бы все дифференциальные уравнения можно было бы преобразовать по Лапласу, то в математике произошла бы революция, так как решение алгебраических уравнение значительно проще дифференциальных. К сожалению, такое преобразование возможно лишь для ограниченного количества уравнений, в том числе для уравнений типовых динамических звеньев (ТДЗ).

Поскольку уравнение апериодического звена приняло вид алгебраического, то его можно записать следующим образом:

Из полученного выражения достаточно легко выделить отношение Х_вых(р) / Х_вх(р), которое называется передаточной функцией и для апериодического звена имеет вид:

У каждого типового динамического звена присутствует ряд типовых частотных характеристик: амплитудно-частотную (АЧХ), фазочастотную (ФЧХ), амплитудно-фазовую частотную (АФЧХ или АФХ), логарифмическую амплитудно-частотную (ЛАЧХ), логарифмическую фазочастотную (ЛФЧХ).

На практике чаще всего используется АФЧХ или АФХ.

Амплитудно-фазовая характеристика это вектор, а график АФХ – годограф этого вектора, то есть кривая на комплексной плоскости, которую описывает конец вектора при изменении частоты ω от 0 до ∞. Вектор характеризуется двумя величинами – длина (скаляр или вектор по модулю) и направление (градиент).

Вектор аналитически можно записать в виде двух проекций на действительную и мнимую оси, и выразить эти проекции через угол α:

После использования формулы Эйлера:

Где |W| — длина вектора или вектор по модулю, i – мнимое число:

Аналитическое выражение для любого вектора АФХ любого типичного динамического звена легко получить из передаточной функции, заменив в ней оператор Лапласа р на выражение iω. Где ω – частота колебаний (ω = 2π/Т), Т – период колебаний.

Для апериодического звена амплитудно-фазовая частотная характеристика (АФХ) имеет вид:

Для записи вектора АФХ в виде проекций на действительную и мнимую ось необходимо произвести следующие преобразования:

Изменяя частоту ω от 0 до ∞ можно построить на комплексной плоскости годораф (график вектора АФХ), представляющий из себя полуокружность (рисунок а)), которая располагается в четвертом квадранте комплексной плоскости. Диаметр полуокружности равен коэффициенту k.

На рисунке б) показана типовая переходная функция апериодического звена. Как видно из графика, она изменяется по экспоненциальному закону. У любой экспоненты есть одно прекрасное свойство – если к любой ее точке провести касательную, а затем точку пересечения касательной с асимптотой и точку касания спроецировать на ось времени, то получится один и тот же отрезок времени на оси времени. Эта проекция, которую называют постоянной времени, соответствует значению коэффициента Т₀ в АФХ и передаточной функции апериодического звена, а ордината асимптоты, к которой стремится экспонента, соответствует коэффициенту k в передаточной функции. Таким образом, по переходной характеристике апериодического звена довольно легко найти коэффициенты Т₀ и k в передаточной функции звена.

Физическим примером апериодического звена может быть конденсатор, при подаче напряжения на который заряд происходит не мгновенно, а с определенной задержкой, или же электродвигатель, который при подаче питания разгоняется не мгновенно, а через какое-то время t. На рисунке в) показан пример установки, которую также можно считать апериодическим звеном (вода – заполняющая бак).

В бак поступает определенное количество воды с расходом Q₁. В то же время из бака вытекает вода с расходом Q₂. Регулируемый параметр в этой системе Х_вых – уровень воды в баке H.

При подаче единичного скачка Q₁ (открыли входной вентиль) уровень воды H в баке повышается. При этом растет гиростатическое давление и возрастает Q₂. Через некоторое время уровень воды H в баке стабилизируется (экспонента приближается к асимптоте). Способность самостоятельно восстанавливать равновесие, которое присуща объектам, аппроксимируемым апериодическим звеном, за счет стока или притока вещества или энергии называют самовыравниванием. Количество самовыравнивания определяет коэффициент р, равный обратному значению коэффициента k в передаточной функции звена, то есть р = 1/k.

В литературе объекты с передаточной функцией апериодического звена называют статическими.