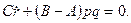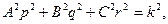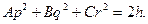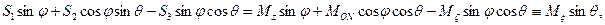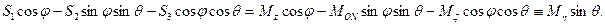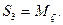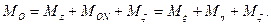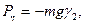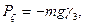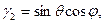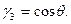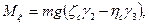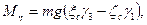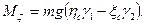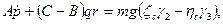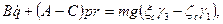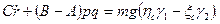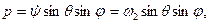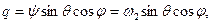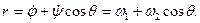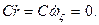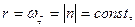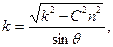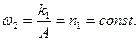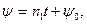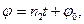Динамические уравнения эйлера для спутника

Динамические уравнения Эйлера

Динамические уравнения Эйлера

• Динамическое уравнение Эйлера для вращения объекта вокруг неподвижной точки под действием силы можно вывести из теоремы об изменении момента движения. Согласно этой теореме, dKoldt = L ^>, (10) Где Ko — момент движения тела относительно неподвижной точки от вращения тела относительно инерциальной системы отсчета. D> | = X — векторная сумма моментов Т внешней силы, действующей на тело (рис. 135). Среди внешних сил есть сила реакции в фиксированной точке.

Когда снаряд находится в движении, его центр тяжести движется так, как если бы в нем была сосредоточена вся масса тела и к нему были приложены все действующие на снаряд внешние силы. Людмила Фирмаль

Когда (10) представляется проекцией на инерциальную (фиксированную) координатную ось, моменты, которые меняются со временем, в зависимости от конкретного случая основных (3) и (4) главных осей, через Kx, Ku, K В том числе обычное уравнение инерции. Это расчет, который уже должен знать движение тела, и сам должен определяться силой, данной. Чтобы избежать этого, Эйлер предложил проецировать вектор (10) на движущуюся ось координат, прикрепленную к вращающемуся телу.

• Для таких осей момент инерции не зависит от времени. Подготовьте векторное уравнение (10) для проекции на оси подвижных координат, закрепленных на движущемся объекте. По этой причине абсолютная производная по времени от момента движения должна быть выражена как относительная производная по формуле Бора. + К. Болезнь.

Это связано с тем, что система перемещения осей координат имеет ту же угловую скорость, что и само тело, с которым эти оси связаны. Представлено векторное поколение для удобства проецирования Удалить вектор в виде определителя, затем развернуть до элементов первой строки, т.е. | J K I шхко = тсс шу юг = / (шу ^ 1-шхх) + | к * к, кг я + j (azKx-axKz) + H (axKy-ayKx), (12) где i, j и H — единичные векторы, ориентированные вдоль осей координат движущейся системы координат.

В разделе упражнений будет показано, что систему векторов можно всегда привести к таким двум векторам, из которых Ъдин лежит на произвольной прямой, не параллельной главному вектору. Людмила Фирмаль

Используйте уравнение (I) для выражения теоремы об изменении момента движения (10) в следующем виде: Рисунок 135 В проекции на ось подвижной координаты, прикрепленной к вращающемуся телу, с учетом (10 ‘) — (12), ^ + — (15) sog = f cos6 4-f, Это представляет проекцию угловой скорости вращения объекта на движущиеся координатные оси, прикрепленные к объекту через углы Эйлера f, 6, f и их производные по времени.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Please wait.

We are checking your browser. gufo.me

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6e34f1a3cff715ee • Your IP : 85.95.188.35 • Performance & security by Cloudflare

Об интегрировании динамических уравнений Эйлера

Общий случай решения задачи о вращении твердого тела вокруг неподвижной точки и, следовательно, решение системы (111.228) и (11.113) дифференциальных уравнений связан с непреодолимыми математическими трудностями. В наиболее простых случаях, когда действующие на тело внешние силы либо приводятся к равнодей­ствующей, линия действия которой проходит через неподвижную точ­ку, либо имеют равный нулю главный момент относительно непо­движной точки, уравнения (111.228) принимают вид

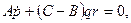
допускают два первых интеграла

Один из этих интегралов получим, если первое из уравнений умножим на р, второе — на q, а третье — на r и результаты сложим;

Преобразование, о котором идет речь, имеет весьма сложный вид:

Предлагаем читателю убедиться в том, что каждое из написанных уравне­ний совпадает с соответствующим уравнением (111.228). При этом следует обра­титься к рис. 81, имея в виду, что

для получения второго интеграла нужно первое из уравнений умно­жить на Ар, второе — на Вq, третье — на Сr и сложить эти произве­дения. Можно показать, что произвольные постоянные, входящие в эти интегралы, имеют простое механическое истолкование, а именно: постоянная k представляет собой абсо­лютную величину кинетического момента отно­сительно неподвижной точки (k = L₀), а по­стоянная h равна, кинетической энергии те­ла (h=T).

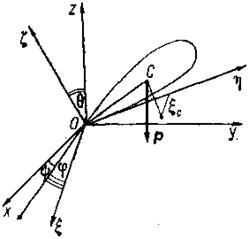
Практический интерес представляет случай, когда твердое тело вращается вокруг непо­движной точки под действием силы тяжести (рис. 120).

Обозначим координаты центра тяжести С в подвижной системе координат ξ_c, η_c, ζ_c. Про­екции силы тяжести Р на подвижные оси име­ют вид

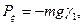
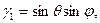
Если обозначить радиус-вектор точки С через г_c, а орты подвижных осей через i, j, k, то момент силы тяжести относительно неподвижной точки О будет

M_O(P)=r_c×P=-mg

и, следовательно, моменты силы Р относительно подвижных осей:

Подставляя эти выражения в уравнения (111.228), получим ди­намические уравнения Эйлера для случая, когда тело вращается вокруг неподвижной точки под действием силы тяжести:

В настоящем курсе не рассматривается вопрос об интегрировании динамических уравнений Эйлера. Заметим лишь, что трудности

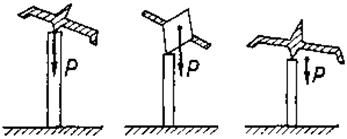
Случай Эйлера Случай Случай

связанные с решением этого вопроса, привели исследователей к рассмотрению частных случаев движения тела вокруг неподвижной точки. Л. Эйлер рассмотрел случай, когда тело под действием силы тяжести вращается вокруг неподвижной точ­ки, совпадающей с центром тяжести тела; Лагранж,— когда

А = В и центр тяжести тела лежит на оси симметрии, проходящей через неподвижную точку. С. В. Ковалевская ис­следовала случай, когда А=В = 2С, а центр тяжести тела находится в экваториальной плоскости эллипсоида инерции.Эти случаи про­иллюстрированы на рис. 121, принадлежащем Н. Е. Жуков­скому. Теория вращательного движения твердого тела вокруг непод­вижной точки получила большое развитие в теории гироскопов, ши­роко применяемых в современной технике.

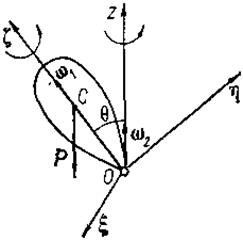
Пример. Рассмотрим случай регулярной прецессии. Этот случай движения тела вокруг неподвижной точки будет иметь место в приближенной теории гироскопа.

Пусть твердое тело имеет материальную ось симметрии ζ, вокруг которой оно вращается с постоянной по величи­не угловой скоростью ω₁, а ось ξ в свою очередь вращается вокруг неподвижной оси г (рис. 122) с угловой скоростью шз, причем ось образует с z постоянный угол нутации θ. Движе­ние тела, при котором соблюдаются указанные выше усло­вия, называется регулярной прецессией, а ω₂ — угловой ско­ростью регулярной прецесии. Тогда кинематические формулы Эйлера (11.113) примут вид:

В силу симметрии А=В. Поэтому из третьего уравнения (111.228) найдем

По (111.212) найдем

Интегрируя эти уравнения, найдем углы Эйлера, т. е. определим вращение тела вокруг неподвижной точки при высказанных предположениях:

θ=const,

где n₂ — постоянная; φ₀, ψ₀ — значения углов φ и ψ в момент t = 0. Таким образом, в случае регулярной прецессии угол нутации 6 остается постоянным, а угол прецессии ψ и угол собственного вращения φ изменяются пропорцио­нально времени.

Дата добавления: 2015-08-08 ; просмотров: 990 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ