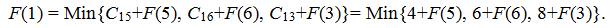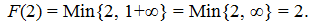Фронтендер пишет нейронки. Уровень сложности «мартышка и уравнение Беллмана»
Количество плюсов под последней статьей говорит о том, что моя подача материала про нейронные сети не вызвала сильного отторжения, поэтому решение — “прочитать, посмотреть что-то новое и сделать новую статью” не заставило себя ждать. Хочется сделать оговорку, что нисколько не претендую на звание того, кто будет учить чему-то и говорить о чем-то серьезном в своей статье. Наоборот, нахожу данный формат — написание статьи или выступление на конференции, способом, когда самому можно чему-нибудь научиться. Ты делаешь что-то, собираешь обратную связь, делаешь что-то лучше. Также это происходит и в нейронных сетях. Кстати о них.
В комментариях к прошлой статье поднялся вопрос про reinforcement learning. Почему бы и нет. Давайте подробнее рассмотрим что это такое.
Как и в прошлый раз, я постараюсь не использовать сложные математические формулы и объяснения, так как сам понимаю на своем примере, что нежные ушки и глазки фронтендера к этому не приспособлены. И как завещал Хокинг, любая формула в популярной работе сокращает аудиторию вдвое, поэтому в этой статье она будет всего одна — уравнение Беллмана, но это уже понятно из названия.
Итак, reinforcement learning, или обучение с подкреплением — это такая группа методов машинного обучения, подходы которой сначала выглядят как методы обучения без учителя, но со временем (время обучения) становятся методами обучения с учителем, где учителем становится сама нейронная сеть. Скорее всего, ничего непонятно. Это не страшно, мы все рассмотрим на примере.
Представим, у нас есть крысиный лабиринт и маленькая лабораторная крыса. Наша цель — научить крысу проходить лабиринт от начала до конца. Но этот лабиринт необычный. Как только крыса, бегая по лабиринту, сворачивает не туда, ее начинает бить током пока она не вернется на правильную дорожку (довольно жестоко, но такова наука). Если же крыса находит конечную точку, то ей дают некоторое кол-во сыра, вознаграждая ее труды.
Наш условный лабиринт
Представляя эту картину, мы можем увидеть все основные составляющие любого проекта с использованием обучения с подкреплением. Во-первых, у нас есть крыса — Агент (agent), наша нейронная сеть, которая мыслит и принимает решения. Во-вторых, у нас есть Окружение или среда (environment) агента — лабиринт, который имеет свое Состояние (state), расположение проходов, мест с котами, финальный островок и так далее. Крыса может принимать решения и совершать определенные Действия (actions), которые могут приводить к разным последствиям. Крыса либо получает Вознаграждение (reward), либо Санкции (penalty or -reward) за свои действия.
Наверное, очевидно, что основной целью является максимизировать свое вознаграждение минимизируя санкции. Для этого нужно принимать правильные решения, а для этого нужно правильно интерпретировать свое окружение. Собственно, для этих задач и пригодилось машинное обучение.
Но, говоря, “мы решили эту проблему при помощи обучения с подкреплением”, мы не сообщаем никакой информации. Данная группа весьма обширна и в данной статье мы познакомимся с самым популярным методом — Q-learning. Идея та же самая, жестоко бить током нашу нейронную сеть, когда та косячит и одаривать всеми благами мира, когда делает то, что нам нужно. Давайте рассмотрим детали.
Семейство методов обучения с подкреплением
Вообще, пусть меня поправят эксперты, Q-learning может не иметь ничего общего с нейронными сетями. Вся цель этого алгоритма — максимизировать значение Q (вознаграждение, полученное за проход от начального состояния до конечного), используя конечные автоматы.
Мы имеем некоторое кол-во состояний (s1, s2 . ), наш агент может находится в одном из этих состояний в каждый момент времени. Цель агента достичь финального состояния.
Пример конечного автомата
Что остается — это заполнить таблицу переходами на следующие состояния. И найти хитрый способ (алгоритм) как мы можем оптимизировать перемещения по таблице, чтобы заканчивать игру в финальном состоянии всегда с максимальным вознаграждением.
Динамическое программирование уравнение беллмана пример
Дисциплина :
МЕТОДЫ ОПТИМИЗАЦИИ
Электронные гипертекстовые методические указания студентам
для выполнения практических и лабораторных работ
Автор : Коднянко В. А.
Работа № 4. Динамическое программирование
Динамическое программирование это способ решения сложных задач путём разбиения их на более простые подзадачи. Часто его применяют к целочисленным задачам оптимизации, сводя их к последовательности целочисленных оптимизационных задач меньшей сложности. С помощью этого метода успешно решают задачи нахождения кратчайших путей, оптимального вложения денежных средств в бизнес, оптимальной загрузки оборудования, оптимального распределения рабочей силы, оптимальном управлении складскими запасами, а также множества других оптимизационных задач.
Ключевая идея в динамическом программировании достаточно проста. Чтобы решить поставленную задачу, требуется решить отдельные части задачи (подзадачи), после чего объединить решения подзадач в одно общее решение. Подход динамического программирования состоит в том, чтобы решить каждую подзадачу только один раз, сократив тем самым количество вычислений. Это особенно полезно в случаях, когда число повторяющихся подзадач экспоненциально велико.
В большинстве случаев динамическое программирование включает представление сложной задачи в виде рекурсивной последовательности более простых подзадач, то есть таких задач, когда решение последующей задачи зависит от найденного решения предыдущей задачи в такой последовательности.
Словосочетание «динамическое программирование» впервые было использовано в 1940-х годах Ричардом Беллманом для описания процесса нахождения решения задачи, где ответ на одну задачу может быть получен только после решения ряда предшествующих ей задач. Вклад Беллмана в динамическое программирование был увековечен в названии уравнения Беллмана, центрального результата теории динамического программирования, который переформулирует оптимизационную задачу в рекурсивной форме.
Термин «программирование» в словосочетании «динамическое программирование» к «традиционному» программированию (написанию программного кода) почти никакого отношения не имеет, это скорее составление программы некоторых действий по решению задачи. Поэтому слово «программа» в данном контексте скорее означает оптимальную последовательность действий для получения решения задачи. К примеру, составление расписания событий на выставке это некоторая программа действий. Программа в данном случае понимается как последовательность событий, ведущих к результату.
Идея метода динамического программирования достаточно проста. Пусть необходимо найти сумму целых чисел
Чтобы применить к решению этой задачи метод ДП необходимо разбить ее на несколько подзадач. Сначала найдем F(1) = 1, Далее F(2) = F(1) + 2, F(3) = F(2) + 3, …
Нетрудно видеть, что общая задача сводится к последовательности вычислительных задач вида
Находя последовательно F(1), F(2), F(3),…, F(n), решим поставленную задачу.
Например, если нужно вычислить сумму 1 + 2 + 3 + 4, то сначала нужно поставить начальное условие F(1) = 1, а затем трижды выполнить рекурсивную формулу F(i) = F(i–1) + i, для i = 2, 3, 4, т. е. вычислить F(2) = F(1) + 2, F(3) = F(2) + 3, F(4) = F(3) + 4.
Итак, чтобы решить некоторую задачу методом ДП необходимо вывести некоторое начальное условие, затем вывести рекуррентную формулу, при помощи которой посредством решения последовательности промежуточных подзадач будет получено решение поставленной задачи.
Решим две оптимизационных задачи методом ДП.
4.1. Задача о лабиринте
Пусть имеется поле, разделенное на клетки, в каждой из которых лежит клад определенной ценности (положительное число), штраф (отрицательное число) либо ничего нет.
На рис. 4.1 дан пример поля в виде матрицы стоимостей C размером 5х5.
Задача заключается в том, чтобы проложить маршрут от ячейки (i, j) = (1,1) до ячейки (i, j) = (5,5), двигаясь вправо или вверх так, чтобы собрать клады наибольшей стоимости.
Решим задачу методом ДП, начиная с конечной ячейки маршрута. Обозначим F(i,j) оптимальный маршрут из ячейки (i, j) в ячейку (5, 5). Очевидно, F(5,5) = 8 – стоимость пути из ячейки (5, 5) в саму себя.
Решением задачи является оптимальная стоимость пути F(1,1) в ячейку (5, 5).
Для верхней строки (i = 5) двигаться по ячейкам можно только вправо, поэтому
Аналогично получим оптимальные пути для последнего столбца (j = 5). Они показаны на рисунке 4.2.
Найдем оптимальный путь F(4,4). Из этой ячейки можно двигаться вправо или вверх. Если двигаться вправо, то путь будет равен F(4,4) = –3 + F(4,5) = 10. Если двигаться вверх, то F(4,4) = –3 + F(5,4) = 9. Поскольку 10 > 9, то двигаться выгоднее вправо и следует пометить лучший путь стрелкой из ячейки (4,4) в (4,5). При этом расчетная формула примет вид F(4,4) = –3 + Max<F(4,5), F(5,4)> = 10 и от ячейки (4,4) на оптимальном маршруте следует двигаться вправо.
С помощью это формулы легко вычислить оптимальный путь из любой ячейки с координатами (i, j)
Это и есть рекуррентная формула для последовательного расчета оптимальных маршрутов из любой ячейки (i,j) в ячейку (5,5).
Используя эту формулу, перемещаясь последовательно по столбцам сверху вниз, и влево, можно заполнить матрицу оптимальных стоимостей и указать оптимальный маршрут.
Видно, что длина оптимального маршрута (на рисунке 7.3 он показан красными стрелками) F(1,1) = 36. Чтобы собрать такую стоимость нужно двигаться по ячейкам (1,1) – (1,2) – (2,2) – (3,2) – (3,3) – (4,3) – (4,4) – (4,5) – (5,5) или ВССВСВВС (восток-север-север-восток-север-восток-восток-север).
4.2. Поиск кратчайшего пути на графе
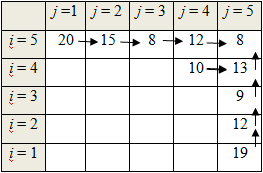
На рис. 4.4 показан пример ориентированного графа, содержащего вершины, через которые можно прокладывать маршруты. Возможные пути перехода из одной вершины в другую соединяют направленные ребра, на которых надписаны расстояния между такими вершинами. Задача состоит в том, чтоб найти кратчайшее расстояние между двумя заданными вершинами.
Пусть необходимо найти кратчайший маршрут из вершины 1 в вершину 4. Задачу решим методом ДП.
Прежде всего выведем начальное условие. Очевидно, F(4) = 0 – расстояние от конечной вершины 4 до самой себя, а P(4) = – маршрут, образованный этой вершиной. Эти отношения являются начальным условием.
Теперь построим необходимую рекуррентную формулу. Очевидно, что кратчайшее расстояние из вершины i можно выразить формулой
Маршрут P(i) найдется по формуле
как объединение текущей вершины i и кратчайшего маршрута P(j), где – j номер той вершины из i, которая доставляет минимум F(i).
Решением задачи будет кратчайшее расстояние F(1) и кратчайший маршрут P(1).
Найдем эти величины для приведенного на рис. 4.4 графа.
1. Из вершины 1 исходит 3 ребра в вершины 5, 6, 3 поэтому
Поскольку F(5) неизвестно, то перейдем к его нахождению. Из вершины 5 есть только один переход – в вершину 2, поэтому
Расстояние F(2) тоже неизвестно, поэтому перейдем к его нахождению. Из вершины 2 есть два перехода – в вершины 4 и 7. До первой из них кратчайший маршрут известен равен нулю, поэтому
Поскольку вершина 7 тупиковая и достичь вершины 4 из нее нельзя, то можно считать, что такой маршрут имеет бесконечную длину и, следовательно,
Cам маршрут из вершины 2 равен P(2) = <2>U <4>= <2,4>.
Двигаясь в обратном направлении, получим F(5) = Min <7+2>= 9, P(5) = .
Сделав еще один шаг назад, найдем
2. В этой формуле неизвестно F(6). Найдем его.
Из вершины 6 есть переходы в вершины 2, 4, 3. Поскольку F(2) и F(4) уже известны, а F(3) еще неизвестно, то
Найдем неизвестное F(3). Из вершины 3 есть только один переход – в вершину 4, для которой оптимальный маршрут известен, поэтому
Очевидно, сам маршрут из вершины 3 равен P(3) = <3>U <4>= .
Теперь можно найти
Из этой формулы видно, что из трех возможных направлений движения из вершины 6, наилучшим оказалось то, которое ведет в вершину 2. Следовательно, кратчайший маршрут
Сделав еще один шаг назад, с учетом того, что F(6) и F(3) теперь известны, найдем
Из этой формулы видно, что кратчайшее расстояние F(1) = 12 соответствует ребру из вершины 1 в вершину 6, поэтому маршрут
будет кратчайшим маршрутом движения из вершины 1 в вершину 4.
4.3. Задача о рюкзаке
Дано k предметов, i-й предмет имеет массу wi > 0 и стоимость ci > 0. Необходимо выбрать из этих предметов такой набор, чтобы суммарная стоимость была максимальна, а их суммарная масса не превосходила массы n (вместимость рюкзака).
Математически задача формулируется следующим образом. Необходимо найти максимум функции
где xi может принимать значение 1 (предмет выбран) или 0 (предмет не выбран.)
Задача укладки рюкзака может быть решена простым перебором всех возможных вариантов значений вектора решений x, число которых равно 2 k , с последующим выбором наилучшего варианта вектора значений. Однако этот способ может быть применен лишь при сравнительных малых значениях k. С увеличением числа предметов количество перебираемых вариантов возрастает экспоненциально, что замедляет расчеты или делает их невозможными.
Применим к решению данной задачи метод динамического программирования.
Обозначим за F(i,j) максимальную стоимость первых i предметов из имеющегося количества k, которые можно оптимально уложить в рюкзак вместимости j. Тогда очевидно F(k,n) будет определять решение поставленной задачи, т. е. максимальную стоимость оптимально отобранных и уложенных в рюкзак предметов.
Рассмотрим свойства функции F(i,j).
Очевидно, F(0, j) = 0 для j = 0, 1, 2, 3, …, n. Это значит, что если в рюкзак не уложен ни один предмет (i = 0), то оптимальная стоимость загруженных предметов равна нулю.
Также очевидно, что F(i, 0) = 0 для i = 0, 1, 2, 3, …, k. То есть, если допустимая масса загрузки в рюкзак равна нулю, то в него ничего нельзя загрузить и, следовательно, оптимальная стоимость загруженных в него предметов также равна нулю.
Эти два условия являются начальными.
Теперь составим необходимую рекуррентную формулу для общего случая. Пусть на некотором шаге оптимизации получена оптимальная стоимость F(i,j).
Для этой стоимости последний товар, который, подвергался загрузке в рюкзак, имеет номер i. Если он попал в рюкзак, то предшествующий ему вариант оптимальной загрузки при первых i–1 предметах, имел оптимальную стоимость F(i–1, j–wi). Тогда оптимальную стоимость F(i,j) можно вычислить через предыдущий оптимальный план загрузки по формуле
как сумму оптимальной стоимости первых i–1 предметов и стоимости i-того предмета.
Однако возможен вариант, что предмет с номером i не попал в рюкзак, тогда оптимальная стоимость F(i,j) будет равна оптимальной стоимости при i–1,предметах, т. е.
Из двух этих вариантов нужно выбрать лучший. Очевидно, его можно найти по формуле
С помощью этой рекуррентной формулы можно вычислить оптимальный способ загрузки первых i предметов, используя известные начальные условия и оптимальный способ загрузки первых i–1 предметов, что позволяет получить конечный оптимальный план загрузки F(k,n).
Рассмотрим решение задачи на следующем примере. Пусть имеется ранец максимальной массы n = 15 и k = 5 предметов с характеристиками веса и стоимости, которые показаны в таблице
Найти наилучший по стоимости способ загрузки такого рюкзака.
Понятно, что все предметы не удастся разместить в рюкзаке, поскольку их суммарный вес 6 + 4 + 3 + 2 + 5 = 20
Составим таблицу, в которую в верхнюю строку занесем возможные значения вместимости рюкзака j = 0, 1, 2,…, 15, а в левый столбец возможные значения номеров предметов i = 0, 1, 2,…, 5.
Далее занесем в таблицу начальные условия F(0, j) = 0 для j = 0, 1, 2, …, n и F(i, 0) = 0 для i = 0, 1, 2, 3, …, k. Эти ячейки помечены желтым цветом.
Теперь приступим к заполнению строки i = 1. Для этого значения рекуррентная формула имеет вид
F(0,–5) является несуществующим значением из-за отрицательного второго аргумента, его во внимание не принимаем и полагаем F(1,1) = F(0,0) = 0.
Двигаясь по строке i = 1, аналогично найдем F(1,1), F(1,2), F(1,3), F(1,4), F(1,5). Эти клетки помечены синим цветом.
Далее перейдем к заполнению строки i = 2. Для нее рекуррентная формула имеет вид
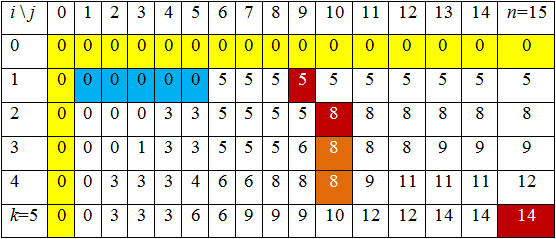
После заполнения строки i = 2 останется аналогичным образом заполнить оставшиеся 3 строки. Полностью заполненная таблица приведена ниже
Как видно из таблицы, оптимальная стоимость предметов, попавших в рюкзак, равна F(k,n) = F(5,15) = 14.
Поскольку F(5,15) = 14, F(4,15) = 12 (с использованием только первых 4 предметов мы можем собрать рюкзак максимальной стоимости 12, а с использованием всех 5 предметов – рюкзак стоимости 14), то предмет 5 попал в рюкзак.
Далее рассмотрим F(4,10) (общая вместимость рюкзака уменьшилась на вес включенного предмета w5 = 6 и теперь равна 8). Поскольку F(4,10) = F(3,10) = F(2,10) = 8, то предметы номер 4 и 3 следует исключить из рассмотрения, поскольку при попытках их загрузки суммарная масса загруженных в рюкзак предметов не изменилась. При этом предмет 2 массой w2 = 3, очевидно, попадает в рюкзак. Если исключить и его, то в рюкзаке остаются предметы общей массой 5. Из первой строки таблицы видно, что это предмет 1 массой w1 = 5.
Таким образом, оптимальный рюкзак будет состоять из предметов 1, 2, 5, его масса будет равна w1 + w2 + w5 = 6 + 4 + 5 = 15, а стоимость c1 + c2 + c5 = 5 + 3 + 6 = 14.
Можно составить рюкзак и по-другому. Обратим внимание, что в строке 4 таблицы осталось еще два элемента F(4,9) = F(4,8) = 8. Если включить в оптимальный рюкзак F(4,9) или F(4,8), т. е. 4-й предмет, то в него попадет еще предмет 1. В этом случае стоимость рюкзака будет также оптимальной c1 + c4 + c5 = 5 + 3 + 6 = 14, а масса w1 + w4 + w5 = 6 + 2 + 5 = 13, то есть такой рюкзак будет даже легче и этот вариант загрузки рюкзака следует признать лучшим.
4.4. Задания для выполнения самостоятельных работ
Ниже приведены задачи, которые следует решить методом ДП. Номер а вариант ов назначает преподаватель.
Вариант 1. Биржа торгует пакетами акций предприятий, количество и предполагаемая прибыль от которых показаны в таблице
| Предприятия | 1 | 2 | 3 | 4 | 5 |
| Пакеты акций | 3 | 4 | 1 | 2 | 3 |
| Предполагаемая прибыль в у. ед. | 3 | 6 | 2 | 3 | 4 |
Инвестор, который имеет денежные средства в количестве 9 у. ед., решил приобрести акции. Какие пакеты акций следует купить инвестору чтоб предполагаемая прибыль от их покупки была максимальной?
Вариант 2. Для ориентированного графа найти кратчайший путь из вершины 5 в вершину 4.
Вариант 3. Продавец товаров, который может двигаться только на север или только на восток, должен пройти по маршруту A , B через опорные пункты, отмеченные кружками. Прибыль, которую он получит при движении в соседний пункт надписана на соответствующем отрезке. Как следует двигаться продавцу, чтоб после завершения маршрута он получил максимальную прибыль? Каким будет размер этой прибыли?
Вариант 4. В банке имеются слитки золота весом 2, 4, 3, 5, 1 кг. Пробравшийся в банк г рабитель может унести не более 13 кг золота. Какие слитки следует грабителю похитить, чтоб их суммарный вес был максимальным?
Вариант 5. Для ориентированного графа найти кратчайший путь из вершины 6 в вершину 9.
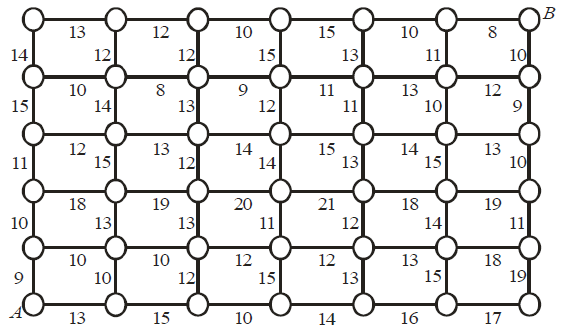
Вариант 6. Путешественнику, который может двигаться только на север или только на восток, необходимо пройти из пункта A в пункт B через опорные пункты, отмеченные кружками. Расстояния между пунктами надписаны на соединяющих их отрезках. Как следует двигаться путешественнику, чтобы пройденный им путь оказался кратчайшим? Какова длина этого пути?
Вариант 7. Многозвенная схема отгрузки товара из пункта S 0 и приемки товара в пункте S 1 показана на рисунке. Отгрузка товара начинается из точки S 0 . Далее он принимается в соседнем пункте справа или выше. При этом издержки составляют сумму, которая надписана на соответствующем ребре. Т овар последовательно передается в соседний пункт, пока не достигнет конечного пункта S 1 . Определить оптимальную последовательность операций по передаче товаров, которая позволяет минимизировать суммарные издержки. Какова сумма этих издержек?
Что такое динамическое программирование
Представляем нашим читателям научно-популярную статью о динамическом программировании, опубликованную на сайте DOU.UA. Автор — Тимофей Антоненко, ML/Python Team Lead в CreatorIQ.
Введение и немного истории
Всем привет. Меня зовут Тимофей, я Python/ML-разработчик, имею 6 лет опыта в индустрии. Занимаюсь исследованиями в области архитектур нейронных сетей в аспирантуре ХНУРЭ, кандидатская связана с нео-фаззи нейронными сетями.
Тема этой статьи важна для тех, кто сталкивается с обработкой данных в своей работе. На практике динамическое программирование может пригодиться вам всего лишь 1–2 раза в жизни, но сам концепт помогает по-другому посмотреть на работу с алгоритмами.
Когда я сам учился решать задачи с помощью этого подхода, у меня часто возникали трудности с интуицией решения. Скажу даже, что однажды из-за задачи по динамическому программированию я ужасно провалил одно собеседование. Ну не получалось у меня рассмотреть нужные зависимости в структурах данных, как я не пытался. Но меня всегда привлекал этот метод, поскольку в нем есть что-то нестандартное, он часто с большим отрывом обыгрывает другие алгоритмы в вычислительной гонке. В общем, по некоторым причинам подход к решению задач с помощью динамического программирования кажется мне не интуитивным. И многие статьи/уроки, которые освещают эту тему, не раскрывают ее с той стороны, с которой мне бы хотелось.
Вот на основании этих мыслей и возникла идея написать материал.
Итак, что же такое динамическое программирование
Начнем с истории (весьма забавной, кстати). Она о Ричарде Беллмане — человеке, который придумал и закрепил в научном сообществе понятие «динамическое программирование». В 1940 году он использовал этот термин для задач, где решение одной части задачи зависело от другой. Затем в 1953-м Беллман изменил и дополнил определение динамического программирования до его текущего вида.
Он забавно описывает ситуацию с именованием этого понятия. Беллману нужно было придумать название, но чиновник, перед которым он тогда отчитывался, сильно ненавидел (математик подчеркивает, что именно «ненавидел») термины и не хотел разбираться с ними. Каждый раз всем сотрудникам приходилось буквально дрожать от страха из-за того, что их босс не может понять что-то и мешает это с грязью в своих невеселых каламбурах. А особенно математические термины!
В связи с этим Беллман много времени и усилий потратил на придумывание названия. Слово «программирование» было выбрано как аналог слову «планирование», которое не подходило по ряду различных причин (у Советов все время было планирование чего-то).
А слово «динамическое» было выбрано исходя из того, что, помимо передачи сути подхода, с ним трудно было придумать что-то унизительное, бранное. Беллман не хотел, чтобы руководитель как-то коверкал его термин. Даже чиновник не смог бы сделать это так легко (у читателей, конечно же, найдется пара вариантов). Вот таким образом и сформировался термин «динамическое программирование».
Официальное определение есть на Википедии. Упрощенное определение от меня: динамическое программирование — это подход к решению задач, который основывается на том, что исходная задача разбивается на более мелкие подзадачи, которые проще решить. И потом решения этих подзадач можно использовать для решения исходной задачи.
Мой друг, который делал ревью статьи, сказал, что все задачи решаются таким образом! Я был повержен этим утверждением и не нашел, что ему ответить.
Потому важные дополнения:
- подход имеет смысл, если решения подзадач использовать эффективно (запоминать, например);
- подзадачи имеют общую структуру, поэтому к их решению можно применить какой-то выработанный однородный способ, а не решать каждую отдельно разными алгоритмами.
В тексте иногда будет использоваться аббревиатура ДП — динамическое программирование.
Пройдемся более детально по этому определению.
1. ДП — это подход к решению задач. То есть это не просто формула или алгоритм, а скорее методология, которая говорит вам, как думать, чтобы решить задачу.
2. Это подход к решению задач, где нужно разбить задачу на более мелкие подзадачи, которые легко решить. К этому утверждению может быть много вопросов.
Что означает «более мелкие подзадачи»? (Можно также сказать «более простые подзадачи»). Ответ: это задачи, которые нужно решить для входных данных меньшего размера. Под меньшим размером можно подразумевать или меньшее число, или массив меньшего размера, или меньшее количество настраиваемых параметров и так далее. Возьмем, например, числа Фибоначчи. Обозначим как Ф(N) — N-е число Фибоначчи. То есть Ф(5) — это пятое число Фибоначчи. Чтобы посчитать пятое число Фибоначчи, нужны третье Ф(3) и четвертое Ф(4) числа Фибоначчи. Вот как раз задачи нахождения третьего и четвертого чисел Фибоначчи и являются более мелкими подзадачами.
Эти более мелкие задачи легко/просто решить. Если вы знакомы с O-нотацией, то я вам скажу просто, что более простая задача O(простая) является легче сложной О(сложная), если О(простая) 
На практике люди часто путают ДП с рекурсией или с методом «разделяй и властвуй». Но здесь весьма просто все прояснить и найти отличия.
В рекурсии вы в некотором месте алгоритма начинаете использовать этот же алгоритм (или его часть) для решения подзадачи. При этом вам все равно, решалась ли эта подзадача раньше. И таким образом строится дерево рекурсии, в котором вы вызываете условную функцию A внутри функции А.
В методе «разделяй и властвуй» имеет значение, на каких данных вы вызываете свою функцию, но тут нет таких хороших инструментов ДП, как мемоизация и табуляция (речь о них пойдет дальше).
Как применять динамическое программирование для решения задач
У программистов могут быть совершенно разные задачи. В одном случае вам нужно просто использовать язык разметки, чтобы что-то нарисовать, в другом — прописать инструкции через ассемблер для эффективной работы процессора.
Но у всех людей работает эта ассоциация — программисты разрабатывают алгоритмы.
И вот представим, что и к вам прилетела свеженькая задача, у которой есть цель и ограничения. Как и в любой задаче, в ней также присутствуют структуры данных и зависимости от других частей системы.
И в один момент вы понимаете, что именно для этой задачи важно быстродействие. Вы можете это понять не сразу. Например, сначала вы решили задачу, потом заметили, что ваше решение медленно работает. Или же вам невдомек, как решить задачу, чтобы результаты вычисления были получены быстрее чем через 100 лет.
Да, наверняка у вас есть/был способ, который решал бизнес-цели задачи. Но когда вы понимаете, что время решения сильно увеличивается (полиномиально, например) при росте количества/значения входных данных, то пора задуматься о ДП.
Прежде чем описать алгоритм, введем два понятия — мемоизация и табуляция.
Мемоизация и табуляция
Мемоизация — оптимизационная техника, которая позволяет запоминать результаты вычислений и потом переиспользовать их тогда, когда нужно сделать такие же вычисления.
Любимый пример: при подсчете седьмого числа Фибоначчи вы можете запомнить четвертое число Фибоначчи и не вычислять его каждый раз, а только один раз.
Также эту технику описывают как «сверху вниз». Причина — на рисунке. Это граф в виде дерева рекурсии для вычисления пятого числа Фибоначчи:
То есть вы сначала решаете большую проблему «сверху» — Ф(5), а потом спускаетесь. Так вот, когда вы, например, первый раз достигли вершины графа Ф(2) и посчитали ее значение, то запоминаете его и второй раз уже не пересчитываете, а достаете из памяти. То же самое и для остальных вершин. В большинстве случаев доставать из памяти намного быстрее, чем пересчитывать.
Табуляция — оптимизационная техника, которая начинает решать подзадачи с самой простой и потом при дальнейшем продвижении решает все более сложные подзадачи, пока не будет решена основная задача. При этом для решения более сложных подзадач используются решения более простых подзадач.
В отличие от мемоизации, этот подход называют «снизу вверх» из-за того, что вы сначала беретесь за самые простые задачи.
На числах Фибоначчи это работает в том случае, когда вы решаете задачу с помощью цикла. То есть Ф(i) = Ф(i-1) + Ф(i-2), где i — это индекс внутри цикла. И если вы уже получили Ф(i-1) и Ф(i-2) на предыдущих итерациях, то текущее вычисление не составит труда.
Понятия мемоизации и табуляции позволяют расширить свой взгляд на программистские хаки для решения задач.
Итак, пошаговый алгоритм для задач динамического программирования
1. Представим, что решение вашей задачи — это результат работы функции Z.
Итого Z(x) = y, где x — входные параметры, y — решение задачи для входных параметров x.
2. Посмотрите, как ведет себя решение задачи для небольших и последовательных значений x. То есть в тех случаях, когда объем вычислений небольшой.
Под «посмотрите» я имею в виду в буквальном значении — напишите все результаты (и то, как они получились) и пробегитесь своими глазами по всем решениям.
Например, если знаете, что х может принимать значения натуральных чисел, то посмотрите на результаты работы функции при:
Если же x — это какой-то массив, то посмотрите, как ведет себя функция Z при разных небольших массивах:
Здесь элементы массива должны удовлетворять требованиям вашей задачи (например, натуральные или положительные и рациональные зависит уже от вашей конкретной задачи).
3. На основании результатов из предыдущего пункта попытайтесь понять общую закономерность.
И, что очень важно, проверьте, есть ли зависимость в результатах вычисления. То есть может y_5 зависеть от y_4 или от y_2. Или, может, данные, которые были получены при вычислении y_3, можно использовать при вычислении y_5. Например, в числах Фибоначчи Ф(5) зависит от Ф(3) и Ф(4).
Бывают случаи, когда нет прямой зависимости между результатами разных вычислений. Или она есть, но ее сложно увидеть, так как для вас эта задача является непривычной.
Мы такие случаи рассмотрим в примерах с задачами.
4. Понять, как использовать увиденную закономерность для решения общей задачи.
Если брать пример с числами Фибоначчи, то это означает, что в процессе решения некоторые значения будет проще сохранить в памяти, а не пересчитывать каждый раз. А это как раз будет мемоизация.
В примерах, где решение задачи для N + 1 можно получить из решения для N, весьма вероятно, что придется хранить в памяти состояние переменных (индексов, указателей) в момент получения решения N.
Простой пример — это заполнения массива числами Фибоначчи через цикл.
(arr[i] = arr[[i-1] + arr[i-2]. На момент вычисления arr[i] у нас в памяти уже были правильные решения для arr[i-1] и arr[i-2].)
Для одномерной задачи это может выглядеть примерно так:
В этом примере нужно посчитать значение произвольной функции S от числа n, то есть S(n). Но во время поиска S(n-1) у вас были еще дополнительные переменные, которые работали с другими элементами прошлых решений. Пусть это будут указатели pointer № 1 и pointer № 2. Также у вас применяется стандартная индексация массива (индекс i может принимать значения из <0, 1, 2, …, n-1>). Тогда выходит, что, следуя алгоритму, для поиска S(n) нужны S(n-1), pointer № 1 и pointer № 2.
Это можно назвать примером табуляции, поскольку для нахождения S(n) вы используете информацию S(n-1), при этом считаете результат снизу вверху: сначала S(1), потом S(2) и так далее, пока не дойдете до нужного S(n).
В двумерном мире все продолжается по аналогии. Например, у вас зависимость от двух координат/переменных. То есть наша функция S теперь зависит от двух переменных — S(i, j). И вы можете легко посчитать решения (или часть решения) по каждой из них при условии, что вторая координата будет константой. В примере ниже мы зафиксировали это значение на числе ноль.
Но вот для получения решения S(3, 3) (или же в более общем виде S(i, j)) вам потребуется:
И вы понимаете, что это не для вас, так как очень много ресурсов/времени нужно потребить.
Подход с помощью ДП как раз и предлагает получить искомое S(3, 3) путем более эффективного использования уже имеющихся решений. Мы будем применять полученные результаты из этих подзадач для нахождения нужного нам главного решения.
В примере ниже мы посчитали результат для S(3, 3), вычисляя при этом не все возможные S(i, j), а только часть из них. Стрелочками показано, как мы двигались по пространству результатов для подзадач.
То есть мы получили значение для S(1, 1) на основании S(0, 1) и S(1, 0). Затем получили S(2, 1) на основании S(1, 1) и S(2, 0). Да, это абстрактный пример, но он весьма хорошо описывает подход, который используется в реальных задачах. Суть в том, что мы:
- часть результатов рассчитываем заранее;
- храним в памяти полученные результаты.
По аналогии вы находите решение и для задач большой размерности. Да, это легко сказать, но универсального ключика под все задачи, к сожалению, нет. Разве что ваш ум.
5. Вот мы и подобрались к тому, чтобы привести наше решение в пригодный для бизнес-целей вид. Время оформлять его. Если нужно, пишем код, получаем решение, радуемся. Ну а если код не нужен, оформляем блок-схему или просто радуемся, что решение есть у нас в голове. (Замечу, однако, что часто решение «в голове» не покрывает все детали задачи.)
По этому пункту особых замечаний и советов я дать не могу. Одна вещь только. Так как для ДП зачастую нужна дополнительная память, то в основном это следующие структуры данных:
- одномерный массив;
- двухмерный массив;
- сколько-будет-нужно-мерный массив;
- хэш-таблица.
Решает ли ДП задачи из реального мира
Да, конечно! ДП решает задачи из реального мира. Хотя это не очень-то легко заметить.
Одна из самых наглядных задач — построение маршрута, который проходит через несколько точек. Приложения для онлайн-карт и сервисы такси часто сталкиваются с подобным вопросом (вероятно, что одни сервисы используют API других сервисов). Например, захотелось вам развести компанию друзей после веселой вечеринки на такси. Ну а как понять, кого отправить домой первым и через какие улицы ехать? Вот здесь и работает с теорией графов наше динамическое программирование. Из классических задач ДП это пересекается с задачей коммивояжера.
Соответственно, похожим является пример в компьютерных сетях, когда пакет данных нужно доставить сразу нескольким адресатам. Алгоритму нужно понять, по какому маршруту и в каком порядке доставить данные во все пункты назначения.
Утилита diff — тоже яркий пример использования ДП. Так как задача состоит в том, чтобы найти похожие подстроки в двух строках, то здесь явно прорисовывается одна из классических задач ДП — нахождение наибольшей общей подпоследовательности.
Вот здесь рассказывается, как смежную с diff задачу приходится решать в реальном приложении. На фронтенде!
Еще интересный пример. Ребята сжимают изображения с помощью ДП. Все вы знаете, что при сжатии иллюстрации используют подходы, где похожие места/одинаковые пиксели записывают через меньшее количество информации. А вот в приведенном примере описан подход того, как можно сжать изображение с модификацией контента изображения и при этом сохранить высокий уровень информативности. То есть если смысловая нагрузка фото была «собака с кошкой на лужайке», то и после обрезания она будет такой. А это уже непростая задача!
Прикладным программистам при использовании этого подхода стоит в первую очередь разделить бизнес-логику и алгоритмическую часть. Чтобы не приходилось потом объяснять продуктовым людям, почему вы упустили баг, в котором берете элемент под индексом 100 (arr[100]) из массива размером в 100. Но это, конечно же, касается не только ДП.
Да, в мире реальных задач аутсорса/аутстаффа решать задачи с помощью ДП приходится нечасто. И вам ни в коем случае не нужно стараться лишний раз придумать себе, где применить ДП. Просто уже достаточно, что вы знаете о таком подходе, понимаете, как он работает, и знаете, где его можно использовать в реальной жизни.
Примеры применение динамического программирования для решения алгоритмических задач
Чтобы лучше разобраться с динамическим программированием, я приведу пример решения трех различных задач. Сложность их возрастает (первая — самая легкая, последняя — самая сложная).
Примечание. Если вы не программист, то можете пропустить этот раздел, так как он, скорее всего, вам покажется скучным. А из-за того, что вы не будете применять знания из примеров на практике, то они быстро выветрятся из головы. Не волнуйтесь, в этом нет ничего плохого.
Задача 1. Восхождение по лестнице
Вы поднимаетесь по лестнице. Чтобы добраться до вершины, нужно преодолеть n ступенек. За один шаг вы можете подниматься на одну или на две ступеньки. Вопрос: сколько существует различных способов подняться?
Для примера покажу один из возможных способов:
- 0 → 1 (мы прошли одну ступеньку за один шаг).
- 1 → 3 (мы прошли две ступеньки за один шаг).
- 3 → 5 (мы прошли две ступеньки за один шаг).
Решение с помощью ДП
Воспользуемся нашим алгоритмом. Итак, пусть у нас есть функция DP_steps(n) — возвращает количество различных способов подняться в зависимости от n ступенек.
(DP_steps это сокращение от Dynamic Programming steps.)
Далее смотрим, как ведет себя решение задачи от различного количества ступенек.
1. DP_steps(1) = 1. Так как существует только один способ подняться на одну ступень — за один шаг преодолеть одну ступень.
2. DP_steps(2) = 2. То есть существует два способа подняться на две ступени. Первый способ — сделать два шага по одной ступени. Второй способ — сделать один шаг в две ступени.
Дальше я упрощу запись и буду указывать количество ступеней за шаг.
3. DP_steps(3) = 3.
Первый способ: 1, 1, 1.
Второй способ: 1, 2.
Третий способ: 2, 1.
4. DP_steps(4) = 5
Первый способ: 1, 1, 1, 1.
Второй способ: 1, 2, 1.
Третий способ: 2, 1, 1
Четвертый способ: 1, 1, 2
Пятый способ: 2, 2.
Теперь попытайтесь понять общую закономерность в результатах. Если у вас есть время и желание подумать, то лучше попытайтесь сначала сами это сделать. Дальше будут описаны детали решения.
Итак, что же можно было заметить? А то, что результаты DP_steps(n) зависят от DP_steps(n-1) и DP_steps(n-2).
И представим, что мы уже знаем DP_steps(2) и DP_steps(3). Каким же будет DP_steps(4)?
Для получения ответа необходимо заметить, что в четвертую ступень можно попасть только из второй и из третьей. А как мы уже добирались до второй и до третьей ступеней, уже неважно. Главное, что мы там уже оказались. А это означает, что нашим ответом будет сумма способов попасть во вторую ступень плюс сумма способов попасть в третью ступень. DP_steps(4) = DP_steps(2) + DP_steps(3), то есть DP_steps(4) = 2 + 3 = 5.
Дальше уже нужно просто запрограммировать решение, и для этого есть несколько способов. Я думаю, что самый очевидный — это создать массив и пробежаться по нему циклом:
dp_steps[i] = dp_steps[i-1] + dp_steps[i-2]
Пусть индекс массива у нас отвечает за количество ступеней (тогда размер массива равен n + 1).
И заранее объявить что:
— dp_steps[0] = 1
— dp_steps[1] = 1
— dp_steps[2] = 2
И после заполнения цикла результат будет просто dp_steps[n].
Если присмотреться, то задача похожа на задачу Фибоначчи. Можете подумать, как решить модификацию этой задачи для случая, когда вы можете за один шаг проскакивать не 1–2 ступени, а 1, 2 или 3 ступени.
Задача 2. Поиск размера самой длинной строго возрастающей подпоследовательности
Пояснение к условию задачи. Подпоследовательность — это последовательность, которая может быть получена из исходной последовательности путем удаления некоторых или никаких (!) элементов из исходной последовательности.
Например, [2, 4, 1] является подпоследовательностью [1, 2, 5, 7, 4, 2, 1]. Чтобы последовательность была строго возрастающей, нужно, чтобы каждый ее элемент был строго больше предыдущего.
На примере массива: пусть у нас есть массив array, то он будет строго возрастающим, если array[i] > array[j] для всех i > j.
- [1, 2, 4] является строго возрастающей последовательностью для [5, 1, 1, 7, 2, 4]. Длина равняется трем.
- Для массива [2, 2, 2] размер самой длинной строго возрастающей последовательности равен 1.
Решение без помощи ДП
Первое, что может прийти в голову — это перебрать все возможные последовательности. То есть итерировать массив по всем его числам и каждый раз, когда встречаем число, которое нарушает возрастающую последовательность, вызывать еще раз метод поиска самой длинной подпоследовательности, но уже начиная с этого числа.
Например, если у нас есть массив [3, 4, 1, 7]. И мы итерируемся по нему:
- Первый элемент — 3, все хорошо.
- Второй элемент — 4, последовательность возрастающая, все хорошо. Длинна равна двум.
- Третий элемент — 1. Ага, возрастающая подпоследовательность нарушена, мы не можем добавить в нее 1.
Тогда мы запускаем новый поиск строго возрастающей последовательности, но уже начиная с 1. То есть вызываем наш метод для массива [1, 7]. И так далее.
В конце мы просто возвращаем размер самой большой строго возрастающей подпоследовательности. Понятно, что если массив будет строго убывающим (например, [7, 6, 5, 4, 3, 2, 1]), то наша функция будет вызываться рекурсивно много раз.
Решение с ДП
Попробуем применить подход ДП. Итак, пусть есть наша функция — length_of_LIS. Где LIS это Longest Increasing Subsequence.
В этой задаче мы не можем просто проверять, как работает функция, когда мы даем ей на вход только одно небольшое натуральное число. Поэтому для того, чтобы посмотреть, как ведут себя результаты функции, придумаем себе какой-то небольшой массив, по которому будет легко найти правильный ответ и человеку.
Например, [1, 3, 2]. Начнем с одного элемента — [1].
length_of_LIS([1]) = 1. Здесь все понятно.
length_of_LIS([1, 3]) = 2. Здесь тоже все понятно, два подряд строго возрастающих числа.
length_of_LIS([1, 3, 2]) = 2. В этом примере у вас может произойти секундная задержка, где вы, увидев число 2, вернетесь и проверите глазами, что только один меньше двух. Затем вы быстренько сравните по длине две последовательности [1, 3] и [1, 2]. Увидите, что они одинаковые, подумаете, нормально ли это, и поймете, что нормально. И затем вернете ответ: 2.
То есть мы видим, что для последнего примера пришлось вернуться назад и найти число поменьше. А если бы массив был такой: [0, 1, 3, 2], мы бы, когда возвращались и нашли 1, должны были бы понимать, что до единички еще есть и 0, который добавляет длины в эту последовательность.
Первое, что подумал: я бы не хотел возвращаться назад к массиву во время того, как я его итерирую. Ведь это на самом деле никак не влияет на размер самой большой строго возрастающей подпоследовательности.
Ведь я точно знаю, что для каждого среза массива (то есть куска массива от нулевого до какого-то элемента) у нас есть решение. Когда мы здесь прибавляем следующий элемент, то решение может поменяться. Но если мы знаем, как образовалось предыдущее решение, то нам уже необязательно проходить еще раз по массиву.
И вот здесь мое решение и решение известного сервиса Leetcode расходятся (мне кажется, что их решение более канонично с точки зрения ДП).
Следующий этап — понять, как можно переиспользовать то, что в данную итерацию массива у нас уже существует решения задачи. И на следующем шаге итерации мы можем это переиспользовать.
Добавим структуру данных — HashMap. Назовем ее просто: saved_lengths. Будем рассматривать saved_lengths как словарь
Ключами этого словаря будут числа, которые встречаются в нашем массиве. А значениями будут (вот здесь внимательно читайте) размеры самых длинных строго возрастающих подпоследовательностей до момента встречи этого числа. Ух, сложно! Но я сейчас все объясню.
Например, на вход нам передали массив [10,9,2,5,3,7,101,18].
Мы начинаем итерироваться по нему:
- 10. Итак, мы встретили это число в массиве и запишем его в saved_lengths. Так как в saved_lengths больше нет элементов меньше 10, то мы знаем, что длина самой длинной строго возрастающей последовательности на данном этапе равна 1.
saved_length = - 9. То же самое. Проверяем, есть ли числа меньше 9 в saved_length. Их там нет. Добавляем в массив ключ 9 и значение 1.
saved_length = - 2. То же самое. Проверяем есть ли числа меньше 2 в saved_length. Их там нет. Добавляем в массив ключ 2 и значение 1.
saved_length = - 5. А вот здесь интереснее! Проверяем, есть ли числа меньше 5 в saved_length. И они там есть. Это 2. Значение для 2 в saved_length равно 1. А это означает, что размер самой длинной строго возрастающей последовательности для 5 равен 1 + 1 = 2. Что произошло: мы посмотрели в saved_length и увидели, что есть числа меньше 5. И для этих чисел у нас было записано, что самая длинная последовательность равна 1. Вот и мы добавили в размер этой последовательности еще единичку, так как 5 — это новый элемент этой последовательности.
saved_length = - 3. Смотрим в saved_length. Там есть одно число меньше 3 — это 2. В saved_length у нас записано значение 1 для ключа 2. Добавляем в saved_length новую пару: ключ = 3, значение = 2.
saved_length = - 7. Здесь у нас новый интересный элемент. У нас есть числа 5 и 3 которые меньше 7. Для обеих длина последовательности равна двум, так что для 7 длина равна 3. То есть для 7 у нас две последовательности длиною в три элемента:
— [2, 5, 7]
— [2, 3, 7]
saved_length = - 101. Здесь та же логика, что и для 7. Только у нас уже длина будет 4, так как 7 меньше 101 и длина последовательности для 7 равна 3. То есть мы прибавляем единичку.
saved_length = - 18. Числа 2, 3, 5 и 7 меньше 18. Самая длинная последовательность из всех чисел у нас для 7 — ее длина равна трем. Значит, для 18 длина будет 4.
saved_length =
Затем мы просто перебираем все значения (а не ключи) в saved_length — максимальный вариант это 4, что и является решением нашей задачи!
Задача 3. О поиске N-го уродливого числа
Пояснение к условию задачи. Под «уродливым числом» (англ. Ugly Number) мы понимаем целое положительное число, простыми делителями которого являются только 2, 3 и 5.
Примеры некоторых уродливых чисел:
- 2 — делится только на 2.
- 6 — делится на 2 и на 3.
- 24 — делится на 2 (3 раза) и на 3 (1 раз), то есть 24 = 2 * 2 * 2 * 3.
Примеры не уродливых чисел:
- 14 — делится на 2 и на 7 (а 7 уже не входит в наш список).
- 220 — делится на 2 (2 раза), на 5 (1 раз) и на 11 (а 11 тоже не входит в наш список). 220 = 2 * 2 * 5 * 11.
Вот список первых 11 уродливых чисел:
1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15.
Задача состоит в том, чтобы найти уродливое число под определенным номером. То есть если нужно первое число, то ответ 1, если десятое — 12.
Обозначим нашу функцию как U_N(n). Она возвращает n-ное уродливое число.
Иногда вместо «уродливое число» я буду использовать аббревиатуру УЧ.
Решение № 1 — в лоб
Алгоритм решения: перебираем все числа подряд начиная с единицы. При этом считаем количество встреченных уродливых чисел. Когда дошли до нужного нам по счету числа — возвращаем его.
Блок-схема для наглядности:
В приведенном выше алгоритме есть функция is_number_ugly. Это не сложная функция, которая проверяет простые делители числа. Если простые делители только 2, 3 и 5, то функция возвращает нам истину (true), иначе же возвращается значение ложь (false).
Самый главный недостаток этого алгоритма в том, что нам для каждого числа нужно делать проверку, уродливое ли оно или нет. А эта задача выполняется не за константное время, поэтому хотелось бы как-то избежать подобных вычислений.
Решение № 2 — подход с помощью динамического программирования
Сначала воспользуемся нашим подходом для понимания того, является ли эта задача той задачей, которую можно решить с помощью ДП.
U_N(1) = 1
U_N(2) = 2
U_N(3) = 3
U_N(4) = и здесь уже первая «мини-нетривиальность». При получении этого числа мы проверяем число 4 на то, является ли оно уродливым. И для выяснения этого делим 4 на 2 (2 раза). И понимаем, что U_N(4) = 4.
U_N(5) = 5
U_N(6) = 6
U_N(7) = а здесь вообще чудеса происходят. Мы делим 7 на 2 — не делится. Делим 7 на 3 — тоже не делится. И даже на 5 не делится! Выходит, что 7 — это первое натуральное число, которое не является уродливым. А что еще интереснее, U_N(7) = 8.
Ну как, вы заметили общую закономерность, которая скажет нам, что эта задача решается с помощью ДП? Скажу честно, я не заметил ее сразу. Но умные ребята заметили. И вот как прийти к этой закономерности:
1. Согласитесь с тем, что каждое уродливое число является результатом произведения чисел 2, 3, 5. Это, собственно, следует из определения уродливых чисел.
2. А это означает, что каждое уродливое число (больше 1) является некоторым другим уродливым числом, умноженным на 2, 3 или 5. Чтобы убедиться в истинности этого утверждения, представьте, что у вас есть сколь угодно большое число M. Если оно уродливое, то значит, делится на 2, 3 или 5. Представим, что на 2. Вот поделим мы его на 2. M/2 = G. Мы знаем, что M — уродливое. А это означает, что если его разделить на 2, то все, что останется, тоже состоит из простых множителей 2, 3, 5.
А значит и G — уродливое. Пример: 100 — уродливое. Его простые множители: 1 * 5 * 5 * 2 * 2 = 100. Разделим мы 100 на 2. 100 / 2 = 50. Это означает, что мы просто убрали один из множителей. Было 1 * 5 * 5 * 2 * 2 = 100, а стало 1 * 5 * 5 * 2 = 50. Мы видим, что 50 тоже состоит из простых множителей, входящих в множество <2, 3, 5>. А значит и 50 — простое число.
3. Предыдущий пункт приводит к мысли, что мы не должны просто перебирать все подряд числа и проверять, являются ли они уродливыми. Мы можем просто сгенерировать нужное количество уродливых чисел. Будет генерировать (N+1)-ое уродливое число исходя из уже имеющихся N уродливых чисел.
Но как это сделать эффективным образом? Дальше я приведу детали решения (по порядку):
- Первое уродливое число равно единице — это из определения.
- Чтобы получить второе УЧ, воспользуемся знанием, что мы его можем получить из уже имеющихся уродливых чисел. У нас пока оно только одно — это 1. Итак, мы знаем, что нужно умножить 1 на 2, 3 или 5. Конечно же, умножим его на 2. Итак, следующее уродливое число это 2.
- У нас уже есть предыдущие уродливые числа — 1 и 2. Как же получить следующее?
Тоже будем умножать. Умножим 1 на 3 и 5 (на 2 уже множили) и умножим 2 на 2, 3 и 5. Следующим по возрастанию числом будет 3. - У нас уже есть 1, 2, 3. Нам тоже нужно их умножать на 2, 3, 5. Но мы уже умножали единицу на 2 и на 3. Мы же не будем делать это каждый раз, чтобы получить новое число, ведь мы получим только старые, которые уже есть. Поэтому будем делать не все умножения. Единицу умножим только на 5, для 2: 2 * 2, 2 * 3, 2 * 5, для 3: 3 * 2, 3 * 3, 3 * 5. Следующее по возрастанию — 4, это результат произведения 2 * 2. Ухты, мы как будто сдвинулись с места и начали умножать числа не только на единицу.
- Пропустим несколько итераций.
- И поймем: нужно хранить ссылки на числа, которые являются уродливыми и результат произведения которых на 2, 3 или 5 не превзошел другие числа в предыдущих итерациях.
Ниже приведена визуализация, которая поможет разобраться с этой идеей:
Вот еще ресурс, где приведена эта визуализация только уже в виде анимации.
Выводы
Динамическое программирование — это подход к решению алгоритмических задач, который может сильно уменьшить время работы программ. При этом он потенциально использует неконстантное количество памяти (то есть чем больше задача, тем больше памяти потребуется для ее решения). Но зачастую затраты по памяти ничтожно малы по сравнению с тем ускорением, которое мы получаем.
ДП редко применяется в ежедневных задачах инженеров ПО и не является тривиальным/нативным подходом. Но понимание того, что такой метод существует и что с его помощью можно значительно улучшить эффективность работы программы — это хорошо как для решения конкретных проблем, так и для мировоззрения специалиста.
Спасибо за ваше внимание! Надеюсь, эта статья вам или помогла, или хотя бы скрасила вечер.
http://smiuk.sfu-kras.ru/kodnyanko/site/met_opt/met_opt/4/4.htm
http://techrocks.ru/2021/02/18/dynamic-programming-explained/