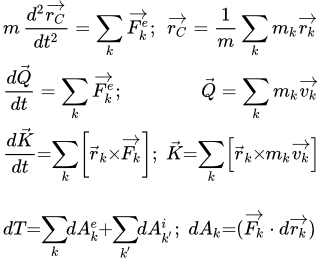Динамика системы основное уравнение в динамике

Динамика твердого тела и системы. Все определения, законы и теоремы

Механическая система. Основные понятия

Свойства внутренних сил

Приводимые ниже свойства внутренних сил являются третьим законом Ньютона для системы материальных точек.

Свойство 1
Векторная сумма (главный вектор) всех внутренних сил системы равна нулю:
.

Свойство 2
Векторная сумма моментов всех внутренних сил системы, относительно произвольной точки O равена нулю:
.

Дифференциальные уравнения движения точек системы

Согласно второму закону Ньютона, дифференциальное уравнение движения материальной точки k массой m_k , входящей в систему, имеет вид:
.
Спроектировав это уравнение на оси декартовой системы координат Oxyz , получим для каждой точки три уравнения:
.

Общие теоремы динамики механической системы

Общие теоремы динамики – это теорема о движении центра масс механической системы, теорема об изменении количества движения, теорема об изменении главного момента количества движения (кинетического момента) и теорема об изменении кинетической энергии механической системы.

Теорема о движении центра масс механической системы

Теорема о движении центра масс механической системы
Произведение массы системы на ускорение ее центра масс равно векторной сумме всех действующих на систему внешних сил:
.

Здесь – масса системы; – ускорение центра масс системы: ;
– скорость центра масс системы: ;
– радиус вектор (координаты) центра масс системы: ;
– координаты и массы точек, из которых состоит система.

Теорема об изменении количества движения (импульса)

Теорема об изменении количества движения в дифференциальной форме
Производная по времени от количества движения (импульса) системы равна векторной сумме всех действующих на систему внешних сил:
.

Теорема об изменении количества движения в интегральной форме
Изменение количества движения (импульса) системы за некоторый промежуток времени равно сумме импульсов внешних сил за тот же промежуток времени:
.

Закон сохранения количества движения (импульса)
Если сумма всех внешних сил, действующих на систему, равна нулю, то вектор количества движения системы будет постоянным. То есть все его проекции на оси координат будут сохранять постоянные значения.

Если сумма проекций внешних сил на какую-либо ось равна нулю, то проекция количества движения системы на эту ось будет постоянной.

Тело переменной массы. Движение ракеты

Уравнение Мещерского
Дифференциальное уравнение движения точки переменной массы называется уравнением Мещерского:
.
Здесь – масса тела, которая является функцией от времени t ; – векторная сумма приложенных к телу внешних сил; – скорость отделяющихся частиц относительно тела.

Реактивная сила направлена в сторону, противоположную истечению отделяющихся частиц (топлива), и определяется по формуле:
,
где – расход топлива (кг/с).

Формула Циолковского

Скорость v движения ракеты под действием одной только реактивной силы определяется по формуле Циолковского:
.
Здесь – начальная скорость ракеты; u – скорость истечения реактивных газов относительно ракеты; – масса сгоревшего топлива; – масса корпуса ракеты с остатками топлива. Когда топливо выгорает полностью, то – это масса корпуса ракеты с полезной нагрузкой.

Отношение первоначальной массы ракеты (с полным запасом топлива) к массе корпуса ракеты называется числом Циолковского:
.
Для достижения первой космической скорости км/с , при , требуется, чтобы скорость истечения реактивных газов была не менее км/с . В современных жидкостных двигателях удается получить скорость истечения км/с . Поэтому, для достижения космических скоростей, ракеты должны быть многоступенчатыми.

Теорема об изменении главного момента количества движения (теорема моментов)

Теорема моментов в инерциальной системе координат

Главный момент количества движения (или кинетический момент) системы является характеристикой вращательного движения. Возьмем систему координат Oxyz с началом в точке O . Тогда , проекции кинетического момента системы на оси координат являются моментами количества движения системы относительно этих осей:
;
;
.

Если система состоит из нескольких частей, то главный момент количества движения системы равен сумме моментов количеств движения отдельных ее частей.

Теорема об изменении главного момента количества движения (теорема моментов)
Производная по времени от главного момента количества движения системы относительно некоторого неподвижного центра O равна сумме моментов всех внешних сил системы относительно того же центра:
(М2) .

Выпишем компоненты уравнения (М2) в неподвижной системе координат Oxyz :
;
;
.

Закон сохранения главного момента количества движения (момента импульса)
Если сумма моментов всех приложенных к системе внешних сил относительно данного неподвижного центра O равна нулю, то главный момент количества движения системы относительно этого центра будет постоянным. То есть все его проекции на оси координат будут сохранять постоянные значения:
.

Часто встречаются случаи, когда система вращается вокруг неподвижной оси. Тогда нужно спроектировать векторное уравнение (М2) на направление этой оси. В результате получим теорему моментов, применительно к вращению относительно оси.

Производная по времени от кинетического момента системы относительно некоторой неподвижной оси равна сумме моментов всех внешних сил системы относительно этой оси. Если сумма моментов всех приложенных к системе внешних сил относительно некоторой неподвижной оси равна нулю, то кинетический момент системы относительно этой оси будет постоянным.

Теорема моментов в системе координат, связанной с центром масс

Кинетический момент системы относительно неподвижного центра удобно использовать в тех задачах, в которых система имеет одну или несколько закрепленных точек. Например при вращении тела или системы тел вокруг точки или оси. Когда таких точек нет, то наиболее удобным в использовании является кинетический момент относительно центра масс в системе координат, в которой центр масс покоится, а оси остаются параллельными осям инерциальной системы отсчета. В общем случае, система отсчета, связанная с центром масс, не является инерциальной, но она не вращается относительно инерциальной системы отсчета.

Главным моментом количества движения системы относительно ее центра масс C называется величина , равная векторной сумме моментов количеств движения всех точек системы относительно центра масс в системе отсчета, в которой центр масс покоится, а оси системы координат параллельны осям инерциальной системы координат:
(М3) .
Здесь – скорости точек системы и скорость ее центра масс в инерциальной системе отсчета. Тогда – скорость точки массой в системе отсчета, связанной с центром масс.

Связь кинетических моментов в различных системах отсчета
Кинетический момент системы относительно неподвижной точки O равен сумме кинетического момента центра масс C , если в нем сосредоточить всю массу системы, и кинетического момента системы относительно центра масс :
(М4) .

То есть можно сказать, что вращение системы вокруг неподвижной точки O складывается из вращения центра масс C вокруг точки O , и вращения элементов системы вокруг центра масс C .

В (М2) ⇑ мы использовали кинетический момент системы, вычисляемый относительно произвольной неподвижной точки в инерциальной системе отсчета. Уравнения для кинетического момента имеют тот же вид, если в качестве полюса взять центр масс C системы.

Теорема моментов относительно центра масс системы
Производная по времени от главного момента количества движения системы относительно ее центра масс C , равна сумме моментов всех внешних сил системы относительно того же центра:
(М5) .

В (М5) мы используем неинерциальную систему координат, начало которой, в течении всего движения системы, находится в центре масс, а оси параллельны осям инерциальной системы координат. Естественно, что если мы выберем инерциальную систему координат, начало которой в данный момент времени совпадает с центром масс, то теорема моментов не изменит своего вида (М5). То есть центр масс обладает такой особенностью, что теорема моментов относительно него имеет одну и ту же форму, как в инерциальной системе отсчета, так и в неинерциальной системе, начало которой на всем протяжении движения совпадает с центром масс, а оси параллельны осям инерциальной системы отсчета. Такая особенность возникает только для центра масс системы. Для других точек, уравнение моментов в неинерциальной системе отсчета не имеет вида (М5).

Кинетический момент твердого тела

Пусть твердое тело вращается с угловой скоростью ω вокруг неподвижной оси Oz . Тогда его кинетический момент относительно этой оси равен произведению момента инерции относительно этой оси на угловую скорость вращения:
.
Если на твердое тело действуют внешние силы, то применяя теорему моментов, находим:
.
Если момент сил относительно оси Oz равен нулю: , то угловая скорость постоянна: .

В произвольном случае, кинетический момент выражается через компоненты угловой скорости и тензора инерции. Пусть, в данный момент времени, скорость точки O тела равна нулю: . То есть точка O является мгновенным центром вращения тела. Тогда компоненты кинетического момента тела относительно точки O определяется по формуле:
.
Здесь – компоненты тензора инерции тела ⇑ относительно точки O . Они связаны с моментами инерции формулами ⇑. Также подразумевается, что индексы p, q принимают значения x, y, z :
.

Здесь мы выбрали в качестве полюса неподвижную (в рассматриваемый момент времени) точку. Если, в качестве полюса выбрать центр масс тела, то компоненты момента импульса определяются по аналогичной формуле:
.
Для других точек, момент импульса выражается через угловую скорость более сложным образом.

В большинстве случаев, наиболее удобным полюсом оказывается центр масс C тела. Тогда, для компонент кинетического момента относительно произвольного центра O , имеем:
.
Здесь – радиус-вектор, проведенный из точки O в точку центра масс C ; m – масса тела; – скорость центра масс; – компоненты тензора инерции относительно точки C . Как видно, первое слагаемое является кинетическим моментом материальной точки, находящейся в центре масс тела и движущейся со скоростью центра масс. Второе слагаемое является вкладом вращения тела относительно его центра масс. То есть, как было указано выше ⇑, кинетический момент твердого тела относительно произвольной неподвижной точки O равен сумме кинетического момента поступательного движения центра масс относительно точки O и кинетического момента вращательного движения тела относительно его центра масс.

Теорема об изменении кинетической энергии

Кинетической энергия системы

Если система состоит из нескольких тел, то кинетическая энергия системы равна сумме кинетических энергий тел, составляющих систему.

Теорема Кенига
Кинетическая энергия системы равна сумме кинетической энергии центра масс C системы, масса m которого равна массе всей системы: , и кинетической энергии этой системы в ее движении относительно центра масс:
.
Здесь – скорость движения центра масс.

Если тело массы m совершает поступательное движение со скоростью , то скорости всех его точек равны . Кинетическая энергия поступательного движения:
(К1) .

Если тело вращается с угловой скоростью ω вокруг неподвижной оси Oz , то кинетическая энергия вращательного движения определяется по формуле:
(К2) ,
где – момент инерции тела относительно оси вращения.

В произвольном случае, кинетическая энергия равна сумме кинетической энергии поступательного движения центра масс и энергии вращательного движения относительно центра масс:
(К3) .
Здесь ω – абсолютное значение угловой скорости вращения тела; CL – ось, проведенная через центр масс, параллельно направлению вектора угловой скорости; – момент инерции относительно оси CL . Направление оси вращения может меняться со временем. Указанная формула дает мгновенное значение кинетической энергии.

Формула (К3) удобна, если тело вращается вокруг неподвижной оси. Если же вектор угловой скорости может менять направление относительно тела, то нам пришлось бы вычислять момент инерции относительно каждого положения оси вращения. В этом случае удобно выразить кинетическую энергию вращения через компоненты тензора инерции относительно центра масс тела:
(К4) .

Работа сил и мощность

Все сказанное в отношении работы и потенциальной энергии в разделе «Динамика материальной точки», имеет место и для динамики системы тел.
См. Работа силы. Мощность Силовые поля и потенциальная энергия
Единственное отличие заключается в том, что там силы приложены только к одной исследуемой точке. Для системы, внешние силы могут быть приложены к разным точкам, составляющих систему. При этом одна сила приложена только к одной точке, но этих сил может быть много. Точку, к которой приложена сила называют точкой приложения силы.

При рассмотрении твердых тел, мы можем упростить реальную систему сил, воспользовавшись результатами статики. Для этого нужно преобразовать сложную систему реальных сил на эквивалентную ей, более простую, систему. Так например, систему сил тяжести, действующих на каждую точку тела, можно заменить одной равнодействующей силой, приложенной к центру масс тела. Тогда все вычисления можно выполнять только для одной силы с точкой приложения в центре масс тела.

Работа при перемещении точки

Элементарная работа , которую совершает сила , при элементарном перемещении ее точки приложения, равна скалярному произведению векторов силы и перемещения:
;
.
То есть она равна произведению модуля вектора силы , перемещения и косинусу угла между ними. Это, в свою очередь, равно произведению касательной компоненты силы к траектории движения, и модуля элементарного перемещения . Здесь – скорость точки приложения силы; – промежуток времени, в течении которого происходит перемещение.

Мощность равна скалярному произведению векторов силы и скорости:
.

Работа , которую совершает сила , при перемещении точки ее приложения из точки в точку , равна сумме (интегралу) элементарных работ:
.

Работа при движении тела

Если тело движется поступательно, то скорости и перемещения всех его точек равны. В этом случае, работа и мощность вычисляются также как и при перемещении точки. Этот случай рассмотрен выше.

Для тела, вращающегося вокруг неподвижной оси Oz , элементарная работа равна произведению момента силы относительно этой оси на элементарный угол поворота dφ :

.
Здесь – мгновенное значение угловой скорости вращения; dt – время, в течении которого происходит поворот на угол dφ .
Мощность равна произведению момента силы на угловую скорость:
.

Для тела, вращающегося вокруг неподвижной точки O , элементарная работа равна скалярному произведению вектора момента силы относительно этой точки на вектор элементарного угла поворота :

.
Вектор элементарного поворота направлен вдоль вектора мгновенной угловой скорости : .
Мощность равна скалярному произведению векторов момента силы и угловой скорости:
.

При произвольном движении твердого тела, мы, произвольным образом, выбираем точку O , связанную с телом, которую называем полюсом. Тогда элементарная работа равна работе, которую совершает сила при перемещении полюса , и работе момента силы относительно полюса при элементарном повороте тела:
.
Заметим, что элементарный угол поворота и угловая скорость вращения не зависят от выбора полюса.
Мощность:
.

Теорема об изменении кинетической энергии системы

Теорема об изменении кинетической энергии системы в дифференциальной форме.
Дифференциал (приращение) кинетической энергии системы при некотором ее перемещении равно сумме дифференциалов работ на этом перемещении всех приложенных к системе внешних и внутренних сил:
.

Теорема об изменении кинетической энергии системы в интегральной форме.
Изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил:
.

Неизменяемая система – это механическая система, в которой расстояние между любыми двумя взаимодействующими точками остается постоянным во все время движения.
Идеальные связи – это связи, для которых сумма элементарных работ их реакций на любом возможном перемещении системы равна нулю.

Для систем с идеальными связями и неизменяемых систем, сумма работ внутренних сил равна нулю: . Для таких систем, изменение кинетической энергии системы равно сумме работ всех внешних сил, приложенных к системе:
.

Коэффициент полезного действия

В машинах и механизмах, совершающих некоторую полезную работу, силы можно разделить на следующие виды.

Движущие силы – это силы, совершающие положительную работу A_затр .
Силы полезного сопротивления – это силы, совершающие отрицательную работу – A_{пол. сопр} , но выполняют полезное действие.
Силы вредного сопротивления – это силы, совершающие отрицательную работу – A_{вр. сопр} , и не выполняющие полезных действий.
Попеременные силы – это силы, совершающие то положительную, то отрицательную работу, но за достаточно большой промежуток времени, их сумма работ равна нулю. Механический коэффициент полезного действия машины – это величина, равная отношению работы полезных сил сопротивления (полезной работы) к работе движущих сил (затраченной на приведение машины в движение):
.

Пусть N_маш – полезная мощность машины; N_дв – мощность двигателя. Тогда
.

Закон сохранения полной механической энергии

Если система движется под действием потенциальных сил, то сумма кинетической T и потенциальной Π энергий сохраняет постоянное значение:
.

Механическая энергия – это сумма кинетической и потенциальной энергии.

Уменьшение механической энергии, как правило, связано с ее превращением в тепловую, электрическую, электромагнитную энергию, энергию звука и электромагнитных колебаний (свет, электромагнитные волны). Увеличение механической энергии связано с обратными процессами превращения различных видов энергии в механическую.

Геометрия масс

Моменты и тензор инерции твердого тела

В этом разделе мы рассматриваем величины, характеризующие распределение массы системы в пространстве.

Сложившаяся система обозначений

Тензор инерции твердого тела

Для вычисления момента импульса и кинетической энергии твердого тела, нам нужно знать всего несколько характеристик тела, величины которых зависят от распределения масс точек, составляющих тело. Эти величины составляют компоненты, так называемого, тензора инерции , который определяется относительно некоторого, предварительно выбранного, центра O , и вычисляется по формуле:
(И1) .
Здесь – координаты точки массы в декартовой системе координат, с началом в выбранном центре O ; при p = q , при p ≠ q . Индексы координат нумеруют цифрами, придерживаясь следующих обозначений:
.

Тензор инерции имеет следующие шесть компонент:
;
;
.
Если в качестве полюса O выбрать центр масс C тела, то компоненты момента импульса и кинетическая энергия тела T вычисляются по относительно простым формулам:
.
Здесь – скорость центра масс тела, – компоненты угловой скорости.

Моменты инерции твердого тела

Пользоваться тензором инерции (И1) ⇑ удобно, поскольку, при решении задач, мы сразу можем применить результаты теории тензорного исчисления. Однако сложилось так, что вместо тензора инерции вводят его отдельные компоненты, придав им специфические названия и обозначения.
Осевые моменты инерции:
;
Центробежные моменты инерции:
.
Все это может привести к путанице. Поэтому компоненты тензора инерции мы будем обозначать буквой I . А сложившиеся названия и обозначения его отдельных компонент – буквой J .

Определения моментов инерции

Свойства моментов инерции

Сумма осевых моментов инерции

Знаки моментов инерции
Осевые моменты инерции не могут быть отрицательными:
.
Центробежные моменты инерции могут быть положительными, отрицательными, или равными нулю.

Симметричность моментов инерции
Центробежные моменты инерции симметричны относительно своих индексов:
.

Все моменты инерции имеют размерность [кг·м 2 ].

Для вычисления моментов инерции сплошных тел, мы от суммирования переходим к интегрированию. При этом массу точки m_k мы заменяем на дифференциал: . Дифференциал массы dm выражаем через плотность μ и элемент объема : . Далее интегрируем по объему тела V :
.

Моменты инерции в разных системах координат

Если мы от начальной системы координат Oxyz перейдем к другой системе O′x′y′z′ , то величины моментов инерции в новой системе будут отличаться от моментов в старой системе координат. Такие переходы называются преобразованиями системы координат.

Повороты системы координат

Сначала рассмотрим случай, когда две декартовы системы координат Oxyz и Ox′y′z′ имеют общее начало O . То есть вторая система получена из первой поворотом вокруг общего центра O . Согласно тензорной алгебре, любой симметричный тензор, поворотом системы координат можно привести к диагональному виду. То есть можно найти такую декартову систему координат, относительно которой все центробежные моменты равны нулю. Оси такой системы координат называются главными осями инерции тела.

Главная ось инерции тела , относительно некоторой точки O – это ось, для которой оба центробежных момента инерции, содержащие индекс этой оси, равны нулю. Например, если ось z – главная ось инерции, то .
Главный момент инерции тела , относительно некоторой точки O – это момент инерции относительно главной оси инерции.
Главная центральная ось инерции тела – это главная ось, проходящая через центр масс тела.
Главный центральный момент инерции тела – это момент инерции относительно главной центральной оси инерции.

Любое тело в пространстве имеет три главные оси инерции и три значения главных моментов инерции (относительно предварительно выбранной точки O ). При этом главные моменты инерции могут иметь равные значения.
Стоит подчеркнуть, что главные оси определяются относительно определенной точки тела. При выборе другой точки, главные оси могут иметь другие направления.

Тело с плоскостью симметрии
Если распределение массы тела в пространстве имеет плоскость симметрии, то любая ось, перпендикулярная к этой плоскости, будет главной осью инерции тела, а две другие главные оси лежат в плоскости симметрии.

Тело с осью симметрии
Если распределение массы тела в пространстве имеет ось симметрии, то эта ось является главной центральной осью инерции.

Параллельность главных осей
Если точка O расположена на главной центральной оси тела, то главные оси, проходящие через эту точку, параллельны главным центральным осям.

Главная ось, не проходящая через центр масс
Главная ось инерции, не проходящая через центр масс тела, является главной осью инерции только в одной точке.

Инвариантность суммы осевых моментов инерции
Если от одной системы координат Oxyz , мы перейдем к другой Ox′y′z′ с тем же началом, то сумма осевых моментов инерции не изменится при переходе от одной системы к другой:
.

По этой причине, величина полярного момента инерции не зависит от поворотов системы координат. То есть является инвариантом относительно поворотов системы координат. Она зависит от выбранного центра, относительно которого определяются моменты инерции.

Момент инерции относительно произвольной оси

Пусть нам известны моменты инерции тела относительно осей Oxyz . И пусть OL – произвольная ось, проходящая через начало O , составляющая углы с осями Ox, Oy, Oz . Тогда момент инерции тела относительно оси OL определяется по формуле:

.
Если оси x,y,z являются главными осями, то
.

Перенос системы координат. Теорема Гюйгенса-Штейнера

Отсюда следует, что осевой момент инерции будет иметь наименьшее значение относительно той оси, которая проходит через центр масс тела.

Моменты инерции некоторых тел

Однородный стержень

Рассмотрим тонкий однородный стержень длины l и массы m . Выберем начало координат O на одном из его концов. Направим ось Ox вдоль стержня; оси Oy и Oz – перпендикулярно. Эти оси будут главными осями инерции стержня относительно центра O . Осевые моменты инерции имеют следующие значения:
.

Центр масс стержня находится по его середине, в точке C ; . Проведем через нее оси координат Cxy′z′ , параллельные предыдущим. Эти оси являются главными центральными осями инерции со следующими значениями осевых моментов:
.

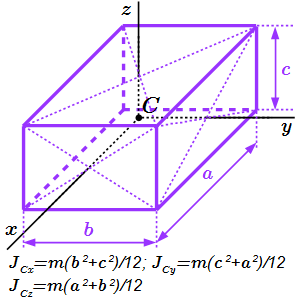
Прямоугольный параллелепипед

Рассмотрим прямоугольный параллелепипед с длинами ребер a, b, c (см. рисунок). Его центр масс C находится в центре параллелепипеда. Оси, проведенные через центр масс параллельно сторонам, будут главными центральными осями инерции. Моменты инерции прямоугольного параллелепипеда:

.

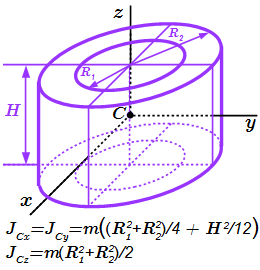
Полый цилиндр

Рассмотрим полый цилиндр высоты H и радиусами . Его центр масс находится на оси цилиндра, на расстоянии от основания. Через точку C проводим главные центральные оси инерции: ось Cz – вдоль оси цилиндра; оси Cx, Cy – перпендикулярно. Моменты инерции полого цилиндра:

.

Однородный сплошной диск

Тонкий обруч

Динамика твердого тела

Свободное движение твердого тела

Рассмотрим твердое тело массы m , перемещение которого не ограничено в пространстве. Пусть на тело действуют внешние силы , приложенных в точках . Для определения уравнений движения, мы воспользуемся теоремой о движении центра масс ⇑, теоремой моментов относительно центра масс системы ⇑, и выражением кинетического момента тела через компоненты угловой скорости ω_q и тензора инерции I_pq тела (в системе координат с началом в центре масс, оси которой параллельны осям неподвижной системы):
(Т1) ;
(Т2) ;
(Т3) .
Здесь – радиус-вектор, проведенный в центр масс тела.

При известных внешних силах , из уравнения (Т1) можно определить закон движения центра масс тела.

Уравнения (Т2)–(Т3) определяют закон движения тела при его вращении. Они записаны в системе отсчета, начало которой находится в центре масс C , а оси параллельны осям инерциальной системы отсчета. Чтобы ими воспользоваться, мы должны найти способ, с помощью которого можно задать положение тела при его вращении. Это можно сделать с помощью углов Эйлера. Тогда оси вращающейся системы координат, связанной с телом, удобно направить вдоль главных центральных осей инерции тела ⇑. Тогда правые части уравнений (Т3) будут выражаться через главные центральные моменты инерций тела ⇑, три угла Эйлера и их производные по времени. Дифференцируя (Т3) и подставляя в (Т2), получим систему дифференциальных уравнений второго порядка для трех углов Эйлера.

Поступательное движение твердого тела

Рассмотрим поступательное движение твердого тела. Для него угловая скорость и угловое ускорение равны нулю: . Тогда момент количества движения постоянен и равен нулю: . Из (Т2) следует, что и главный момент всех внешних сил относительно центра масс должен равняться нулю: .
Дифференциальные уравнения поступательного движения определяются по формулам (Т1) ⇑:
.
Здесь – проекции внешней силы на оси координат. При поступательном движении, все точки тела имеют равные скорости и равные ускорения. Потому определив закон движения одной точки – центра масс , мы получаем закон движения произвольной точки A :
.

Плоское движение твердого тела

Рассмотрим плоское движение твердого тела. Выберем инерциальную систему координат Oxyz . Оси Ox и Oy направим в плоскости движения. Тогда положение тела полностью определяется тремя величинами – двумя компонентами радиус-вектора центра масс C : ; и углом поворота φ . Внешние силы также лежат в рассматриваемой плоскости. Кинетический момент направлен вдоль оси z и выражается через угловую скорость и момент инерции относительно оси, проходящей через центр масс C , перпендикулярно плоскости движения: .

Уравнения (Т1)-(Т3) ⇑ принимают вид:
(Т4) ;
(Т5) .
Здесь – проекции внешней силы на оси координат; – это алгебраический момент силы относительно центра C – то есть проекция момента силы на ось Oz .

Вращение твердого тела вокруг неподвижной оси

Рассмотрим вращение твердого тела вокруг неподвижной оси Oz . Выберем декартову систему координат. Ось Oz направим вдоль оси вращения; оси Ox и Oy – перпендикулярно. Считаем, что перемещение параллельно оси вращения отсутствует. Тогда это плоское движение. Оно происходит в плоскости Oxy . Положение тела определяется только углом поворота φ вокруг оси вращения.

Применяя теорему моментов ⇑ и связь момента с угловой скоростью ⇑, получим дифференциальное уравнение вращения твердого тела вокруг неподвижной оси:
(Т6) .
Здесь – момент инерции тела относительно оси вращения; – вращающий момент – то есть сумма моментов всех внешних сил относительно оси вращения.

Вводя угловое ускорение , дифференциальное уравнение вращения примет вид:
.
Оно аналогично уравнению прямолинейного движения под действием силы F_x :
.

Если вращающий момент является постоянной величиной: , то уравнение (Т6) имеет решение:
.
Здесь – угол поворота и угловая скорость вращения в начальный момент времени ; – угловое ускорение, постоянная величина.

Физический и математический маятники

Далее мы будем приводить данные только для плоского движения маятника. То есть мы считаем, что маятник совершает колебания вокруг неподвижной оси.

Уравнение вращательного движения физического маятника имеет вид:
.
Здесь ось вращения проходит через точку O ; φ – угол поворота между осью маятника и вертикальной прямой; J_O – момент инерции маятника относительно оси вращения; P =mg – сила тяжести, действующая на маятник массы m ; a – расстояние от оси вращения O до центра масс C маятника; g – ускорение свободного падения. Введем обозначение: . Тогда
.

Рассмотрим малые колебания . При этом . И мы получаем уравнение гармонических колебаний:
.
Общее решение этого уравнения имеет вид:
.
Здесь – постоянные, которые определяются из начальных условий.

Во многих случаях удобно выразить общее решение уравнения малых колебаний через амплитуду α и начальную фазу колебаний β :
.
Величина k называется угловой частотой колебаний. Период колебаний: . Для малых колебаний, период не зависит от амплитуды. Этот результат является приближенным. При увеличении амплитуды такая зависимость появляется.

Математический маятник – это материальная точка, подвешенная на нерастяжимой невесомой нити, и совершающая колебания под действием силы тяжести. 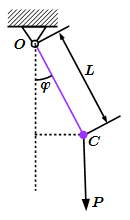Математический маятник.

Математический маятник является частным случаем физического маятника. Пусть L – длина нити математического маятника. Его центр масс C находится в материальной точке: L = |OC| . Момент инерции: . Выразив силу тяжести P через массу m и ускорение свободного падения g , получим угловую частоту колебаний:
.

Теперь вернемся к физическому маятнику. Если положить , то частота физического маятника будет совпадать с частотой математического маятника длины L :
.

Приведенная длина физического маятника – это длина математического маятника, частота колебаний которого совпадает с частотой колебаний рассматриваемого физического маятника.
Центром качаний физического маятника называется точка K на оси физического маятника, находящаяся на расстоянии его приведенной длины от точки подвеса.

Свойство взаимности
Если физический маятник подвесить за центр качаний K , то его частота колебаний не изменится, а прежняя точка подвеса O станет центром качаний нового маятника.

Положение центра качания
Центр качаний всегда расположен ниже центра масс:
.

Принцип Даламбера

Суть принципа Даламбера состоит в том, чтобы задачи динамики свести к задачам статики. Для этого предполагают (или это заранее известно), что тела системы имеют определенные (угловые) ускорения. Далее вводят силы инерции и (или) моменты сил инерции, которые равны по величине и обратные по направлению силам и моментам сил, которые по законам механики создавали бы заданные ускорения или угловые ускорения

Принцип Даламбера
Если в любой момент времени к каждой точке системы приложить силы инерции и реально действующие силы, то полученная система сил будет находиться в равновесии, и к ней можно применять уравнения статики.

Рассмотрим пример. Путь тело массы m совершает поступательное движение и на него действуют внешние силы . Далее мы предполагаем, что эти силы создают ускорение центра масс системы . По теореме о движении центра масс, центр масс тела имел бы такое же ускорение, если бы на тело действовала сила . Далее мы вводим силу инерции:
.
После этого задача динамики:
.
Превращается в задачу статики:
;
.

Для вращательного движения поступают аналогичным образом. Пусть тело вращается вокруг оси z и на него действуют внешние моменты сил . Мы предполагаем, что эти моменты создают угловое ускорение ε_z . Далее мы вводим момент сил инерции M И = – J_z ε_z . После этого задача динамики:
.
Превращается в задачу статики:
;
.

Принцип возможных перемещений

Принцип возможных перемещений применяется для решений задач статики. В некоторых задачах, он дает более короткое решение, чем составление уравнений равновесия. Особенно это касается систем со связями (например, системы тел, соединенные нитями и блоками), состоящих из множества тел

Принцип возможных перемещений.
Для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении системы была равна нулю.

Возможное перемещение системы – это малое перемещение, при котором не нарушаются связи, наложенные на систему.

Общее уравнение динамики (принцип Даламбера — Лагранжа)

Принцип Даламбера — Лагранжа – это объединение принципа Даламбера с принципом возможных перемещений. То есть, при решении задачи динамики, мы вводим силы инерции и сводим задачу к задаче статики, которую решаем с помощью принципа возможных перемещений.

Принцип Даламбера — Лагранжа.
При движении механической системы с идеальными связями в каждый момент времени сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы равна нулю:
.
Это уравнение называют общим уравнением динамики.

Уравнения Лагранжа

Число обобщенных координат n совпадает с числом степеней свободы системы.

Если, при возможном перемещении системы, изменяются все координаты, то работа, совершаемая внешними силами при таком перемещении, имеет вид:
δA = Q ₁ δq ₁ + Q ₂ δq ₂ + . + Q_n δq_n .
Тогда обобщенные силы являются частными производными от работы по перемещениям:
.

Для потенциальных сил с потенциалом Π ,
.

Уравнения Лагранжа – это уравнения движения механической системы в обобщенных координатах:

Здесь T – кинетическая энергия. Она является функцией от обобщенных координат, скоростей и, возможно, времени. Поэтому ее частная производная также является функцией от обобщенных координат, скоростей и времени. Далее нужно учесть, что координаты и скорости являются функциями от времени. Поэтому для нахождения полной производной по времени нужно применить правило дифференцирования сложной функции:
.

Использованная литература:
А. П. Маркеев, Теоретическая механика, «Ижевская республиканская типография», 1999.
Н. Н. Никитин, Курс теоретической механики, «Высшая школа», 1990.
С. М. Тарг, Краткий курс теоретической механики, «Высшая школа», 2010.
А. А. Яблонский, Курс теоретической механики, часть 2, динамика «Высшая школа», 1986.

Автор: Олег Одинцов . Опубликовано: 20-07-2015 Изменено: 23-08-2019

2. Математическое описание систем автоматического управления

Публикую первую часть второй главы лекций по теории автоматического управления.
В данной статье рассматриваются:

2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
2.2. Линеаризация уравнений динамики САУ (САР)
2.3. Классический способ решения уравнений динамики

Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.

Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях

При составлении уравнений, описывающих нестационарные процессы в САУ (САР) и которые в дальнейшем будем называть уравнениями динамики, система “разбивается” на отдельные элементы (звенья), для каждого из которых не существует проблем в записи соответствующего уравнения динамики.

На рис. 2.1.1 представлено схематичное представление САУ (звена) в переменных «вход-выход», где x(t) (или u(t)) — входное воздействие, а y(t) — выходное воздействие, соответственно. Нередко входное воздействие будет называться управляющим, а выходное воздействие — регулируемой величиной (переменной).

При составлении уравнений динамики используются фундаментальные законы сохранения из разделов “Механики”, “Физики”, “Химии” и др.

Например, при описании перемещения узла какого-то механизма силового привода используются законы сохранения: момента, энергии, импульса и др… В теплофизических (теплогидравлических) системах используются фундаментальные законы сохранения: массы (уравнение неразрывности), импульса (уравнение движения), энергии (уравнение энергии) и др

Уравнения сохранения в общем случае содержат постоянные и нестационарные члены, причем при отбрасывании нестационарных членов получают так называемые уравнения статики, которые соответствуют уравнениям равновесного состояния САУ (звена). Вычитанием из полных уравнений сохранения стационарных уравнений получают нестационарные уравнения САУ в отклонениях (от стационара).

где: — стационарные значения входного и выходного воздействий;
— отклонения от станционара, соотвесвенно.

В качестве примера рассмотрим «технологию» получения уравнений динамики для механического демпфера, схематическое изображение которого представлено на рис. 2.1.2.

Согласно 2-му закону Ньютона, ускорение тела пропорционально сумме сил, действующих на тело:

где, m — масса тела, F_j — все силы воздействующие на тело (поршень демпфера)

Подставляя в уравнение (2.1.1) все силы согласно рис. 2.2, имеем:

где — сила тяжести; — сила сопротивления пружины, — сила вязконо трения (пропорциональна скорости поршеня)

Размерности сил и коэффициентов, входящих в уравнение (2.1.2):

Предполагая, что при t ≤ 0 поршень демпфера находился в равновесии, то есть

перейдем к отклонениям от стационарного состояния:
Пусть при t>0 . Тогда, подставляя эти соотношения в уравнение (2.1.2), получаем:

если , то уравнение принимает вид:

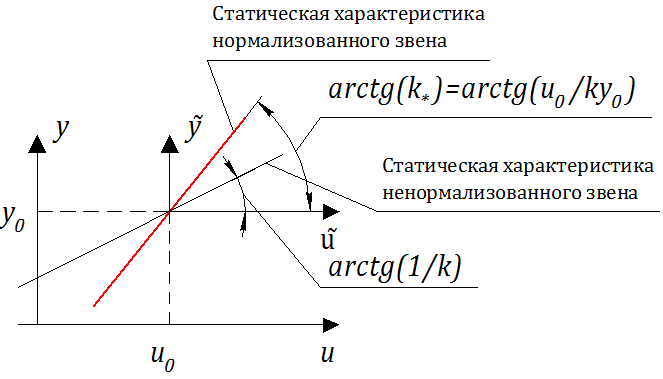
Соотношение (2.1.4) – уравнение звена (демпфера) в равновесном (стационарном) состоянии, а соотношение (2.1.5) – статическая характеристика звена – демпфера (см. рисунок 2.1.3).

Вычитая из уравнения (2.1.3) уравнение (2.1.4), получаем уравнение динамики демпфера в отклонениях:

тогда, разделив на k, имеем:

Уравнение (2.1.6) — это уравнение динамики в канонической форме, т.е. коэффициент при Δy(t) равен 1.0!

«Легко» видеть, что коэффициенты перед членами, содержащими производные, имеют смысл (и размерность!) постоянных времени. В самом деле:

Таким образом, получаем, что:
— коэффициент перед первой производной имеет размерность [c] т.е. смысл некоторой постоянной времени;
— коэффициент перед второй производной: [];
— коэффициент в правой части (): [].
Тогда уравнение (2.1.6) можно записать в операторной форме:

, что эквивалентно

где: — оператор диффренцирования;
-линейный дифференциальный оператор;
— линейный дифференциальный оператор, вырожденный в константу, равную .

Анализ уравнения (2.1.6.а) показывает, что такое уравнение имеет размерные переменные, а также размерными являются все коэффициенты уравнения. Это не всегда удобно. Кроме того, если реальная САР (САУ) состоит из многих звеньев, выходными воздействиями которых являются различные физические переменные (скорость, температура, нейтронный поток, тепловой поток и т.д.), то значения коэффициентов могут различаться на большое число порядков, что ставит серьезные математические проблемы при численном решении уравнений динамики на компьютере (поскольку числа в компьютере всегда представляются с какой-то точностью). Одним из наилучших способов избежать численных трудностей является принцип нормализации, т.е. переход к безразмерным отклонениям, которые получены нормированием отклонения на стационарное значение соответствующей переменной.

Введем новые нормированные (безразмерные) переменные:

Подставляя эти соотношения в уравнение (2.1.2), имеем:

Поддчеркнутые члены выражения в сумме дают 0 (см. 2.1.4) Перенося в левую часть члены, содержащие , и, разделив на , получаем:

где: — коэффициент усиления, причем безразмерный.

Проверим размерность коэффициента

Использованный выше «технический» прием позволяет перейти к безразмерным переменным, а также привести вид коэффициентов в уравнении динамики к легко интерпретируемому виду, т.е. к постоянным времени (в соответствующей степени) или к безразмерным коэффициентам усиления.

На рис. 2.1.4 представлены статические характеристики для механического демпфера:

Процедура нормировки отклонений позволяет привести уравнения динамики к виду:

где дифференциальные операторы.

Если дифференциальные операторы — линейные, а статическая характеристика САУ (звена) – тоже линейна, то выражение (2.1.8) соответствует линейному обыкновенному дифференциальному уравнению (ОДУ).

А если – нелинейные дифференциальные операторы, или , то уравнение динамики — нелинейное. Под нелинейными действиями понимаются все математические действия, кроме сложения (+) и вычитания (-).

Пример создания модели демпфера можно посмотереть здесь: «Технология получения уравнений динамики ТАУ»

2.2. Линеаризация уравнений динамики САУ (САР)

Практически все реальные системы автоматического управления (САУ) являются нелинейными, причем нелинейность САУ может определяться различными причинами:

1. Нелинейностью статической характеристики.
2. Нелинейностью динамических членов в уравнениях динамики.
3. Наличием в САУ принципиально нелинейных звеньев.

Если в замкнутой САУ (САР) нет принципиально нелинейных звеньев, то в большинстве случаев уравнения динамики звеньев, входящих в систему, могут быть линеаризованы. Линеаризация основана на том, что в процессе регулирования (т.е. САУ с обратной связью) все регулируемые величины мало отклоняются от их программных значений (иначе система регулирования или управления не выполняла бы своей задачи).

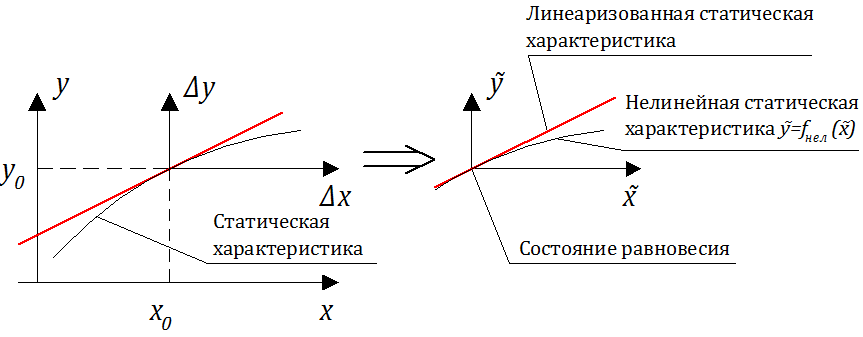
Например, если рассмотреть управление мощностью энергетического ядерного реактора, то главная задача САР — поддержание мощности на заданном (номинальном) уровне мощности. Существующие возмущения (внутренние и внешние) “отрабатываются” САР и поэтому параметры ядерного реактора незначительно отличаются от стационарных. На рис. 2.2.1 представлена временная зависимость мощности ядерного реактора, где нормированные отклонения мощности ΔN /N₀ Рис. 2.2.1 – Пример изменения мощности реактора

Рассмотрим некоторое звено (или САР в целом), описание динамики которого можно представить в переменных “вход-выход”:

Предположим, что динамика данного звена описывается обыкновенным дифференциальным уравнением n-го порядка:

Перенесем в левую часть уравнения и запишем уравнение в виде%

где -– функция регулируемой переменной и ее производных, а также управляющего (входного) воздействия и его производных, причем F – обычно нелинейная функция.

Будем считать, что при t ≤ 0 САУ (звено) находилось в равновесии (в стационарном состоянии). Тогда уравнение (2.2.2) вырождается в уравнение статической характеристики:

Разложим левую часть уравнения (2.2.2) в ряд Тейлора в малой окрестности точки равновесного состояния .

Напомним, что разложение в ряд Тейлора трактуется следующим образом: если , то «простое» разложение функции в ряд Тейлора в окрестности точки будет выглядеть так:

C учетом вышеприведенного разложение принимает вид:

Предполагая, что отклонения выходных и входных воздействий незначительны, (т.е.:), оставим в разложении только члены первого порядка малости (линейные). Поскольку , получаем:

Подставляя соотношение (2.2.4) в уравнение (2.2.2), и перенося множители при у и u в разные части получаем уравнения:

Коэффициенты — постоянные коэффициенты, поэтому уравнения 2.2.5 — линейное дифференциальное с постоянными коэффициентами.

В дальнейшем нами будет часто использоваться операторная форма записи уравнений динамики:

где – оператор дифференцирования;
— линейный дифференциальный оператор степени n;
— линейный дифференциальный оператор степени m, причем обычно порядок оператора выше порядка оператора :

Уравнения (2.2.5) и (2.2.6) — уравнения динамики системы (звена) в отклонениях.

Если исходное уравнение (2.2.1) — дифференциальное уравнение в физических переменных (температура, скорость, поток и т.д.), то размерность коэффициентов может быть произвольной (любой).

Переход к нормализованным отклонениям позволяет “упорядочить” размерность коэффициентов. В самом деле, разделив уравнение (2.2.5) на начальные условия (значения в нулевой момент времени) и выполнив некоторые преобразования, получаем:

Приведение уравнения динамики САУ (звена) к нормализованному виду позволяет “унифицировать” размерность коэффициентов уравнений: ==>

Если вынести в правой части (2.2.7) коэффициент за общую скобку и разделить все уравнение на , то уравнение принимает вид:

или в операторном виде:

Линеаризация уравнений динамики и нормализация переменных позволяют привести уравнения динамики САУ (звена) к виду, наиболее удобному для использования классических методов анализа, т.е. к нулевым начальным условиям.

Пример

Выполнить линеаризацию уравнения динамики некоторой «абстрактной» САР в окрестности состояния (x₀, y₀), если полное уравнение динамики имеет вид:

Нелинейность полного уравнения динамики проявляется в следующем:

• во-первых, в нелинейности статической характеристики:

• во-вторых, слагаемое в левой части — чисто нелинейное, так как действие умножения является нелинейным.

Выполним процесс линеаризации исходного уравнения, динамики без разложения я ряд Тейлора, основываясь на том, что в окрестности состояния (x₀, y₀) нормированные отклонения управляющего воздействия и регулируемой величины намного меньше 1.

Преобразования выполним в следующей последовательности:

1. Перейдем к безразмерным переменным (нормализованным);
2. Выполним линеаризацию, отбросив нелинейные члены 2-го и выше порядков малости.

Перейдем к новым безразмерным переменным:

Заметим, что:
.

Подставляя значения x(t) и y(t) в исходное уравнение:

Удаляем полученного уравнения уравнения стационара: , а так же пренебрегая слагаемыми второго прядка малости: , получаем следующее уравнение:

Вводим новые обозначения:

Получаем уравнения в «почти» классическом виде:

Если в правой части вынести за общую скобку и разделить все уравнение на , то уравнение (линеаризованное) принимает вид:

Процедура нормализации позволяет более просто линеаризовать уравнение динамики, так как не требуется выполнять разложение в ряд Тейлора (хотя это и не сложно).

2.3. Классический способ решения уравнений динамики

Классический метод решения уравнений динамики САУ (САР) применим только для линейных или линеаризованных систем.

Рассмотрим некоторую САУ (звено), динамика которой описывается линейным дифференциальным уравнением вида:

Переходя к полной символике, имеем:

Выражение (2.3.2) — обыкновенное дифференциальное уравнение (ОДУ), точнее неоднородное ОДУ, так как правая часть ≠ 0.

Известно входное воздействие x(t), коэффициенты уравнения и начальные условия (т.е. значения переменных и производных при t = 0).

Требуется найти y(t) при известных начальных условиях.

где: — решение однородного дифференциального уравнения y_<част.>(t) $inline$ — частное решение. $inline$

Будем называть решение однородного дифференциального уравнения , собственным решением, так как его решение не зависит от входного воздействия, а полностью определяется собственными динамическими свойствами САУ (звена).

Вторую составляющую решения (2.3.3) будем называть , вынужденным, так как эта часть решения определяется внешним воздействием , поэтому САУ (САР или звено) “вынуждена отрабатывать” это воздействие:

Напомним этапы решения:

1) Если имеется уравнение вида , то сначала решаем однородное дифференциальное уравнение:

2) Записываем характеристическое уравнение:

3) Решая уравнение (2.3.5), которое является типичным степенным уравнением, каким-либо способом (в том числе и с помощью стандартных подпрограмм на компьютере) находим корни характеристического уравнения
4) Тогда собственное решение записывается в виде:

если среди нет повторяющихся корней (кратность корней равна 1).

Если уравнение (2.3.5) имеет два совпадающих корня, то собственное решение имеет вид:

Если уравнение (2.3.5) имеет k совпадающих корней (кратность корней равна k), то собственное решение имеет вид:

5) Вынужденную часть решения можно найти различными способами, но наиболее распространены следующие способы:
а) По виду правой части.
б) Методом вариации постоянных.
в) Другие методы…

Если вид правой части дифференциального уравнения – относительно несложная функция времени, то предпочтительным является способ а): подбор решения. .

6) Суммируя полученные составляющие (собственную и вынужденную), имеем:

7) Используя начальные условия (t = 0), находим значения постоянных интегрирования . Обычно получается система алгебраических уравнений. Решая систему, находим значения постоянных интегрирования

Пример

Найти аналитическое выражение переходного процесса на выходе звена, если

Решение. Запишем однородное ОДУ:
Характеристическое уравнение имеет вид: ; Решая, имеем: тогда:

где — неизвестные (пока) постоянные интегрирования.

По виду временной функции в правой части запишем как:

Подставляя в исходное уравнение, имеем:

Суммируя , имеем:

Используя 1-е начальное условие (при t = 0), получаем: , а из 2-го начального условия имеем:

Решая систему уравнений относительно и , имеем:
Тогда окончательно:

Что бы проверить результ, выполним моделирование процесса в SimInTech, для этого преобразуем исходное уравнение к виду:

Создадим модель SimInTech, содержащую исходное динамическое уравнение и полученное аналитическое решение, и выведем результаты на один график (см. рис. 2.3.1).

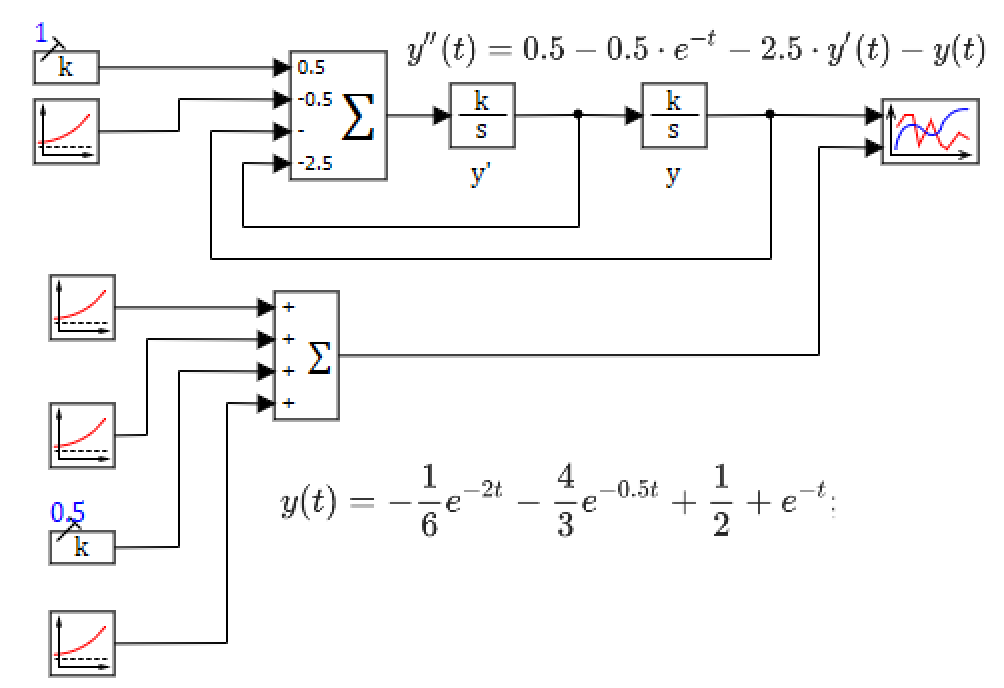
Рис. 2.3.1 – структурная схема для проверки решения

На рис. 2.3.2 приведено решение по вышеприведенному соотношению и численное решение задачи в среде SimInTech (решения совпадают и линии графиков «наложены» друг на друга).

iSopromat.ru

Рассмотрим общее уравнение динамики механической системы, которое также называется принципом Даламбера-Лагранжа:

Объединяя этот принцип с принципом возможных перемещений для систем с идеальными связями получаем уравнение:

которое называют общим уравнением динамики (или принципом Даламбера-Лагранжа).

При движении механической системы с идеальными связями в каждый момент времени сумма элементарных работ всех приложенных активных сил и сил инерции на любом возможном перемещении системы будет равна нолю.

Поскольку в уравнении присутствуют силы инерции, а следовательно и ускорения, то эти уравнения представляют собой дифференциальные уравнения движения механической системы с идеальными связями.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах