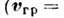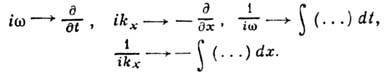Дисперсионное уравнение название величин их размерности

ДИСПЕРСИО́ННОЕ УРАВНЕ́НИЕ

ДИСПЕРСИО́ННОЕ УРАВНЕ́НИЕ, со­от­но­ше­ние, свя­зы­ваю­щее час­то­ты $ω$ и вол­но­вые век­то­ры $\boldsymbol k$ соб­ст­вен­ных гар­мо­нич. волн ( нор­маль­ных волн ) в ли­ней­ных од­но­род­ных сис­те­мах: не­пре­рыв­ных сре­дах, вол­но­во­дах, пе­ре­даю­щих ли­ни­ях, пе­рио­дич. струк­ту­рах и др. Д. у. за­пи­сы­ва­ет­ся в яв­ном $[ω=ω(\boldsymbol k)]$ или не­яв­ном $[f(ω, 𝑘)=0]$ ви­де. В изо­троп­ных сре­дах час­то­та за­ви­сит толь­ко от мо­ду­ля вол­но­во­го век­то­ра: $ω=ω(𝑘)$ . В тех слу­ча­ях, ко­гда за­ви­си­мость $ω(\boldsymbol k)$ не­од­но­знач­на, вы­де­ля­ют од­но­знач­ные вет­ви Д. у. $ω=ω_n(\boldsymbol k) (\textsf <где >n=1, 2, . ),$ со­от­вет­ст­вую­щие нор­маль­ным мо­дам сис­темы, т. е. со­во­куп­но­стям нор­маль­ных волн с оди­на­ко­вой струк­ту­рой. Гра­фич. изо­бра­же­ние кор­ней Д. у. на плос­ко­сти $(𝑘 , ω )$ на­зы­ва­ет­ся дис­пер­си­он­ной кри­вой.

ДИСПЕРСИОННОЕ УРАВНЕНИЕ

ДИСПЕРСИОННОЕ УРАВНЕНИЕ — уравнение, связывающее частоту колебаний ω и волновой вектор к плоской волны, зависящей от времени и координат по закону

Д. у. выводится из уравнений, описывающих рассматриваемый процесс, и определяет дисперсию волн (см., напр., случай электродинамич. процессов в [1], [2]). В зависимости от характера задачи оно может быть использовано для определения частот колебаний по волновому вектору ε_n = ε_n(k) или величин волновых векторов по их направлению и частоте колебаний.

Первый случай тесно связан с решением задачи Коши и исследованием устойчивости положения равновесия, соответствующего тривиальному решению уравнений рассматриваемого волнового процесса. С помощью разложения начальных условий в интеграл Фурье решение задачи Коши может быть записано в виде суперпозиции плоских волн с частотами ε_n(k). Если при нек-ром действительном k среди этих частот имеется хотя бы одна с отрицательной мнимой частью, то это означает существование ограниченных начальных возмущений, к-рым соответствуют экспоненциально нарастающие решения, т. е. неустойчивость.

Второй случай решения Д. у. связан с задачами возбуждения монохроматич. колебаний внешними источниками, гармонически зависящими от времени.

Лит.: [1] Ландау Л. Д., Лившиц Е. М., Электродинамика сплошных сред, М., 1957; [2] Силин В. П., Рухадзе А. А., Электромагнитные свойства плазмы и плазмоподобных сред, М., 1961.

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д — Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.

Дисперсионное уравнение

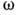
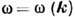
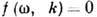
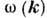
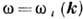
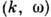
Дисперсионное уравнение — соотношение, связывающее циклич. частоты и волновые векторы k собственных гармонич. волн (нормальных волн)в линейных однородных системах: непрерывных средах, волноводах, передающих линиях и др. Д.у. записывается в явном или неявном виде. В тех случаях, когда зависимость неоднозначна, выделяют однозначные ветви Д.у.: (где n= 1, 2, . ), соответствующие нормальным модам системы, т. е. совокупностям нормальных волн с одинаковой (в т. ч. поляризационной) структурой. Графич. изображение корней Д. у. на плоскости наз. дисперсионной кривой.

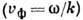
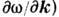
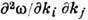
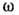
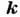
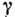
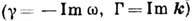
Д. у. эквивалентно полному кинематич. описанию волновых процессов в системе. В частности, Д. у. определяет фазовые скорости гармонич. волн в направлении k , групповые скорости перемещения квазигармонич. одномодовых волновых пакетов, расплывание пакетов (зависящее от величин вторых или более высоких производных). В области комплексных значений и Д. у. определяет временные и пространственные Г инкременты (или декременты) процессов распространения волн (см. Дисперсия волн).

Д. у. являются следствием динамических (в общем случае интегродифференциальных) ур-ний движения и краевых условий на границах раздела сред. И наоборот, по виду Д. у. иногда (при наличии определённой априорной информации о системе) или во всех случаях, когда Д. у. представлено через полиномы по 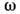и k, могут быть восстановлены динамич. ур-ния процессов с помощью замены

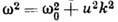
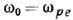
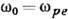
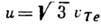
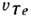
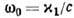
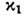
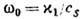
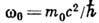
Д. у. позволяет установить общность между волновыми движениями разл. природы: так, напр., одно и то же соотношение соответствует: 1) эл—магн. волнам в изотропной плазме (при этом — плазменная частота, u=c- скорость света в вакууме); 2) плазменным волнам (, , — тепловая скорость электронов); 3) волнам в радиоволноводах (u=c, , -поперечное волновое число, определяемое размерами, конфигурацией волновода, типом и номером моды); 4) волнам в волноводах акустических (u=c_S— скорость звука. ); 5) элементарной частице в релятивистской волновой механике (и = с,, m₀ — масса покоя).

В плавно неоднородных средах, где гармонические во времени поля можно представить в виде

,

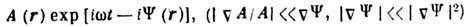
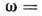
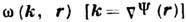
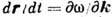
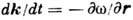
обобщением Д. у. является уравнение эйконала , к-рое совпадает при фиксиров. значении координаты r с Д. у. в соответствующей однородной среде. Ур-нию эйконала можно сопоставить систему лучевых ур-ний (см. Геометрической оптики метод): , . Аналогичным образом Д. у. обобщается на системы с медленно меняющимися во времени параметрами (параметрические колебательные системы).

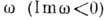
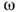
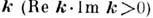
При исследовании нелинейных систем Д. у. позволяет описать волновые процессы вблизи стационарных состояний и установить их устойчивость или характер их неустойчивости. При этом Д. у. составляется для линеаризов. ур-ний, описывающих малые отклонения от стационарного состояния. По виду Д. у. можно определить тип неустойчивости: если действительным k соответствуют комплексные значения , то имеет место абсолютная неустойчивость системы, если действительным соответствуют комплексные значения , неустойчивость является конвективной (см. Неустойчивость в колебательных и волновых системах).

Существует обобщение Д. у. на существенно нелинейные стационарные волновые процессы (периодические нелинейные волны или уединённые волны — солитоны). В этом случае нелинейное Д. у. связывает амплитуду стационарной волны с её структурными параметрами — характерными временами и масштабами (см. Нелинейные колебания и волны).

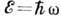
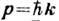
При квантовом подходе Д. у. приобретает смысл соотношения между энергией и импульсом (см. Дисперсии закон).

Литература по дисперсионному уравнению

1. Крауфорд Ф., Волны, пер. с англ., 3 изд., M., 1984;
2. Уизем Дж., Линейные и нелинейные волны, пер. с англ., M., 1977.

M. А. Миллер, Г. В. Пермитин

Дело в том, что в его постановке и выводах произведена подмена, аналогичная подмене в школьной шуточной задачке на сообразительность, в которой спрашивается:
— Cколько яблок на березе, если на одной ветке их 5, на другой ветке — 10 и так далее
При этом внимание учеников намеренно отвлекается от того основополагающего факта, что на березе яблоки не растут, в принципе.

В эксперименте Майкельсона ставится вопрос о движении эфира относительно покоящегося в лабораторной системе интерферометра. Однако, если мы ищем эфир, как базовую материю, из которой состоит всё вещество интерферометра, лаборатории, да и Земли в целом, то, естественно, эфир тоже будет неподвижен, так как земное вещество есть всего навсего определенным образом структурированный эфир, и никак не может двигаться относительно самого себя.

Удивительно, что этот цирковой трюк овладел на 120 лет умами физиков на полном серьезе, хотя его прототипы есть в сказках-небылицах всех народов всех времен, включая барона Мюнхаузена, вытащившего себя за волосы из болота, и призванных показать детям возможные жульничества и тем защитить их во взрослой жизни. Подробнее читайте в FAQ по эфирной физике.