Дисперсионное уравнение волн в волноводе

Основной тип поля в прямоугольном волноводе

На рис.4.1.1 показан прямоугольный волновод, представляющий собой прямоугольную металлическую трубку с тщательно отполированной внутренней поверхностью.

Рис.4.1.1. Волновод — металлическая труба, внутри которой распространяется электромагнитная волна.

Для определения распределения напряженностей электрического и магнитного полей в составе электромагнитной волны в волноводе необходимо решить уравнения Максвелла с учетом граничных условий на металлических стенках волновода: . Будем искать поля через векторный потенциал , который удовлетворяет векторному волновому уравнению:

В волноводе нет диэлектрических или магнитных вкладышей, поэтому диэлектрическая и магнитная проницаемости в волновом уравнении представлены проницаемостями свободного пространства (вакуума).

А) Решение уравнений Максвелла для прямоугольного волновода для случая , .

Будем искать простейшее решение. Положим векторный потенциал равным

, (4.1.1)

А скалярный потенциал независящим от координат и времени. Заданному таким образом векторному потенциалу соответствует .

Связь потенциалов и напряженностей полей:

(4.1.2)

Будем искать решение в виде волны, распространяющейся вдоль оси волновода Z:

(4.1.3)

Тогда векторное волновое уравнение превращается в скалярное волновое уравнение относительно Ау:

(4.1.4)

С граничными условиями: Ау = 0 При , (т. к. при , ) или для введенной функции :

при , (4.1.5)

То уравнение (4.1.4) можно переписать в виде:

(4.1.6)

Где ,

, K -волновое число волны в свободном пространстве,

— Продольное волновое число для волновода или фазовая постоянная распространяющейся волны,

— поперечное волновое число.

(4.1.7)

Полученное уравнение (4.1.7) носит название Дисперсионного уравнения.

Для волновода принято обозначение:

(4.1.8)

Где — Длина волны в волноводе, так что дисперсионное уравнение связывает длину волны в волноводе с длиной волны в свободном пространстве на той же частоте.

Найдем из (4.1.6). Решение (4.1.6) ищем в виде:

Используя граничные условия (4.1.5), получим систему алгебраических уравнений относительно C1 и C2.

Система однородных алгебраических уравнений имеет решение, если определитель системы равен нулю:

или (4.1.9)

Это условие может быть выполнено, если

(4.1.10)

Где

Разные дают разные картины распределения поля в поперечном сечении волновода. Это — условие квантования решений уравнений Максвелла:

(4.1.11)

Вспомним, что , где — длина волны в свободном пространстве. Тогда

(4.1.12)

При n = 1 функция F (х) Определяет простейший тип поля прямоугольного волновода.

Б) Распределение поля в прямоугольном волноводе в случае простейшего типа поля.

Собирая вместе (2.1.3) и (2.1.13), получим для случая N = 1:

(4.1.14)

Используя (4.1.2), (4.1.3) и (4.1.13) получим:

,

(4.1.15)

Полученное решение имеет продольную компоненту магнитного поля. Такое решение принято называть магнитным типом поля и обозначать символом HN, m, где N и M порядок квантования полученных решений вдоль осей X и Y . Полученное решение отвечает магнитному типу поля при N = 1 и M = 0. Структура и эпюры полей в прямоугольном волноводе при волне типа приведены на рис.4.1.2.

Рис.4.1.2. Силовые линии электрического и магнитного полей основного типа поля в прямоугольном волноводе.

Назовем отношение Еу К Нх Волновым сопротивлением волновода:

(4.1.16)

Из (4.1.15) получаем:

(4.1.17)

На рис.4.1.2 показано распределение поля в фиксированный момент времени. Картина поля смещается вдоль оси z со скоростью vG.

(4.1.18)

VG — Скорость движения поверхности равных фаз или фазовая

Скорость волны в волноводе.

Рис.4.1.3. иллюстрирует линии поверхностного тока на внутренней поверхности волновода.

Рис. 2.1.3. Линии тока проводимости на внутренней поверхности прямоугольного волновода с основным типом поля.

В) Критическое значение длины волны волновода.

Для рассматриваемого нами простейшего случая N = 1 выражение (4.1.12) можно переписать следующим образом:

или (4.1.19)

Где λ — длина волны в свободном пространстве. В случае заполнения волновода средой с проницаемостью — λ соответствует длине волны в среде, Т. е.

На рис.2.1.4, а показана зависимость длины волны в волноводе от длины волны в свободном пространстве в случае вакуумного заполнения волновода.

Рис.4.1.4.Частотная дисперсия в радиоволноводе: а) длина волны в волноводе в функции от длины волны в вакууме б) зависимость частоты от фазовой постоянной.

Электромагнитная волна, у которой длина волны в вакууме больше критической длины волны волновода (), не может распространяться в волноводе. Для основного типа поля в прямоугольном волноводе .

Фазовая постоянная волны в волноводе

(4.1.20)

При Фазовая постоянная волны в волноводе β становится мнимым число, так что при поле, возбуждающееся в волноводе, уже не представляет собой волну, а экспоненциально затухает без изменения фазы.

Г) Групповая скорость волны в волноводе.

Итак, мы нашли фазовую скорость волны в волноводе.

(4.1.21)

Где с — скорость света в свободном пространстве при . Чему же равна групповая скорость волны в волноводе? В Главе 2 было получено выражение для групповой скорости (2.1.12). Перепишем его еще раз:

(4.1.22)

Введем понятие критической частоты волновода как

(4.1.23)

И запишем β Как функцию , используя (4.1.20) и (4.1.23)

(4.1.24)

Полученные соотношения иллюстрируются рис. 4.1.4, б. Они устанавливают ту же связь между частотой и фазовой постоянной, что и дисперсионное уравнение (4.1.7). Продифференцируем (4.1.24)

И подставим в (4.1.22). Тогда зависимость групповой скорости волны в волноводе от частоты примет вид:

(4.1.25)

Используя понятие критической частоты, выражение (4.1.21) для фазовой скорости можно записать как

(4.1.26)

Тогда из (4.1.25) и (2.1.26) получим:

(4.1.27)

При понижении частоты фазовая скорость в волноводе растет, а групповая падает при . Это означает, что сигнал в волноводе при распространяться не может.

На рис.4.1.5. показаны зависимости от частоты фазовой и групповой скоростей волн в волноводе при вакуумном заполнении.

Заметим, что связь между фазовой и групповой скоростями, которая определяется соотношением (4.1.27), не универсальна. Она справедлива только в частном случае волновода, несущего электромагнитную волну.

Рис.4.1.5. Фазовая и групповая скорости волны в волноводе в функции от частоты.

Д) Поток мощности через поперечное сечение волновода.

Воспользуемся вектором Пойнтинга (см. рис.4.1.6).

Согласно теореме Пойнтинга средний по времени поток активной мощности Р, проходящей через поперечное сечение S волновода в направлении его оси, может быть вычислен из соотношения:

,

Где вектор Пойнтинга , — комплексно-сопряженная амплитуда вектора напряженности магнитного поля.

Для основного типа поля имеем:

— волновое сопротивление волновода. Тогда

(4.1.28)

Из (4.1.17) и (4.1.19) следует, что (4.1.29)

Рис.2.1.6. Вектор Пойнтинга в прямоугольном волноводе с основным типом поля.

Вычисляя интеграл от вектора Пойнтинга по поперечному сечению волновода, получим поток мощности вдоль оси волновода:

(4.1.30)

— амплитуда напряженности электрического поля.

На рис.4.1.8 показано распределение векторов напряженности электрического поля, магнитного поля и вектора Пойнтинга в поперечном сечении волновода.

Рис.4.1.7. Векторы Е, Н и П в поперечном сечении волновода в функции координаты.

Преобразуем несколько выражение (4.1.30). Используя (4.1.29), получим:

. (4.1.31)

Используя выражение для групповой скорости (4.1.25), можем полученное соотношение для потока мощности через поперечное сечение волновода переписать так:

. (4.1.32)

Полученное соотношение можно интерпретировать следующим образом: При распространении волны объемная плотность энергии электромагнитного поля переносится через поперечное сечение волновода с групповой скоростью. В случае, когда , перенос энергии по волноводу прекращается.

Что будет, если изменить знак у β? Пре этом изменится знак у , а также направление вектора Пойнтинга. Таким образом, если изменить направление распространения волны в смысле направления движения поверхности постоянной фазы, то изменится и направление потока мощности.

В прямоугольном волноводе

В прямоугольном волноводе могут распространяться электрические и магнитные волны — собственные моды волновода. Специфической особенностью любого закрытого волновода независимо от формы его поперечного сечения и диэлектрического заполнения, является дискретный характер спектра собственных мод, являющихся решениями уравнений Гельмгольца (1).

Найдем решение уравнений (1) при следующих граничных условиях:

(3)

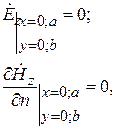
где a и b — поперечные размеры волновода (см. рис. 1).

Решениями уравнений являются выражения для компонент электромагнитного поля для электрических и для магнитных волн. Электрические волны:

(4)

(5)

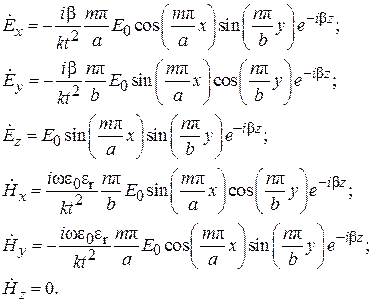
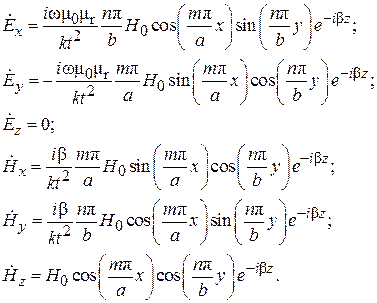
Каждая мода имеет свою дисперсионную кривую, определяемую дисперсионным уравнением. Спектр продольных волновых чисел для прямоугольного волновода:

, (6)

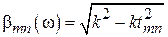
где k — волновое число в неограниченном пространстве; 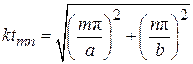; m, n = 0;1;2;… — поперечное волновое число в волноводе.

Каждое из значений bmnсоответствует моде Emnили Hmn, называемой собственной, модальные индексы m и n характеризуют число вариаций компонент поля вдоль осей x и y соответственно. Поле в поперечном сечении волновода представляет собой стоячие волны. Индекс m показывает сколько полуволн стоячей волны укладывается вдоль широкой стенки волновода, а модальный индекс n — вдоль узкой стенки волновода.

Введем для продольного и поперечного волновых чисел следующие соотношения:

,

где λви Vф- длина волны и фазовая скорость волны в волноводе; 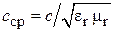— скорость света в среде с электрофизическими параметрами εrи mr; с = 3×108м/с — скорость света в вакууме; — критическая длина волны.

Перепишем продольное волновое число с учетом введенных обозначений

(7)

и выведем соотношения для длины волны и фазовой скорости

(8)

(9)

. (10)

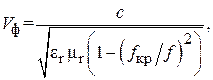
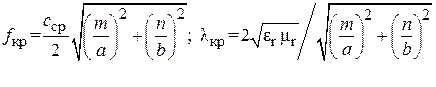
Критические частота fкри длина волны lкропределяют диапазон рабочих частот и длин волн волновода. Собственную моду волновода, имеющую минимальную критическую частоту (частоту отсечки), или максимальную критическую длину волны, называют основной модой волновода. Для прямоугольного волновода основной модой является волна H10. Существованию единственной — основной — моды соответствует одномодовый режим работы волновода.

Волновод, работающий в режиме отсечки (при частотах ниже критической) для всех мод, называют запредельным волноводом.

Анализ структуры электромагнитного поля любой волны высшего типа следует начинать с преобразования системы уравнений (4) или (5) с учетом конкретных значений индексов m и n рассматриваемой волны. После этого следует изобразить картины силовых линий векторов E и H данной волны.

Большую помощь в решении этой задачи может оказать следующее правило. Структуру поля волны Н₁₀ можно считать базовой при построении картин силовых линий векторов E и H собственных волн Н_m0 и Н_0n . Так, например, для волны Н₂₀ картина силовых линий векторов E и H в поперечном сечении волновода получается путем двукратного воспроизведения базовой структуры вдоль широкой стенки волновода (с учетом фазовых соотношений соседних структур); для волны Н₃₀ – трехкратным воспроизведением, и т. д. Для волны Н₀₁ базовая структура будет повернута на угол 90°; для волны Н₀₂ – повернута на 90° и воспроизведена дважды и т.д. (см. рис. 4).

Рис. 4. Силовые линии векторов E и H для различных типов волн:

а – для волны Н₂₀, б – для волны Н₃₀

Несколько сложнее решается задача построения картины силовых линий векторов E и H собственных волн, у которых индексы m и n оба не равны нулю. В этом случае необходимо сначала построить картину силовых линий волны Н₁₁ , которая затем, в зависимости от конкретных значений индексов m и n, будет воспроизводиться требуемое число раз вдоль широкой и узкой стенок волновода. Таким образом, для собственных волн типа Н_mn базовой структурой является структура поля волны Н₁₁ (рис. 5).

Рис. 5. Силовые линии векторов E и H для волны Н₁₁

При построении картин силовых линий векторов E и H собственных волн Е_mn базовой является структура поля собственной волны E₁₁. Картина силовых линий векторов E и H этой волны в поперечном сечении волновода изображена на рис. 6.

Рис. 5. Силовые линии векторов E и H для волны E₁₁

Волновое сопротивление собственных мод в прямоугольном волноводе вводится как отношение поперечных к направлению распространения волны компонент комплексных амплитуд векторов поля волны:

. (11)

ДИСПЕРСИО́ННОЕ УРАВНЕ́НИЕ

ДИСПЕРСИО́ННОЕ УРАВНЕ́НИЕ, со­от­но­ше­ние, свя­зы­ваю­щее час­то­ты $ω$ и вол­но­вые век­то­ры $\boldsymbol k$ соб­ст­вен­ных гар­мо­нич. волн ( нор­маль­ных волн ) в ли­ней­ных од­но­род­ных сис­те­мах: не­пре­рыв­ных сре­дах, вол­но­во­дах, пе­ре­даю­щих ли­ни­ях, пе­рио­дич. струк­ту­рах и др. Д. у. за­пи­сы­ва­ет­ся в яв­ном $[ω=ω(\boldsymbol k)]$ или не­яв­ном $[f(ω, 𝑘)=0]$ ви­де. В изо­троп­ных сре­дах час­то­та за­ви­сит толь­ко от мо­ду­ля вол­но­во­го век­то­ра: $ω=ω(𝑘)$ . В тех слу­ча­ях, ко­гда за­ви­си­мость $ω(\boldsymbol k)$ не­од­но­знач­на, вы­де­ля­ют од­но­знач­ные вет­ви Д. у. $ω=ω_n(\boldsymbol k) (\textsf <где >n=1, 2, . ),$ со­от­вет­ст­вую­щие нор­маль­ным мо­дам сис­темы, т. е. со­во­куп­но­стям нор­маль­ных волн с оди­на­ко­вой струк­ту­рой. Гра­фич. изо­бра­же­ние кор­ней Д. у. на плос­ко­сти $(𝑘 , ω )$ на­зы­ва­ет­ся дис­пер­си­он­ной кри­вой.