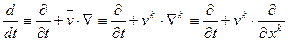Дивергентная форма уравнения баланса энергии
Дивергентная формулировка (1.13) задачи (1.10) описывает закон сохранения величины \(<\rm\phi >\left(x,t\right)\). Если проинтегрировать уравнение (1.13) по произвольному отрезку \(\left[x_<1>^ <*>,x_<2>^ <*>\right]\in \left[x_<1>^<> ,x_<2>^<> \right]\), получим:
Левая часть этого равенства представляет изменение интеграла от искомой функции по отрезку \(\left[x_<1>^ <*>,x_<2>^ <*>\right]\) во времени, правая часть — разность потоков на его границах. Если потоки на границах равны нулю, то полный интеграл по отрезку сохраняет свое значение. По этой причине дивергентную форму дифференциальных уравнений иногда называют «консервативной» формой уравнений.
Все физические процессы, происходящие в макромире, подчиняются четырем фундаментальным законам сохранения: закону сохранения массы, закону сохранения импульса, закону сохранения момента импульса и закону сохранения полной энергии. Применительно к одномерным нестационарным задачам механики сплошных сред актуальны только три из них — в одномерном случае выполняется либо закон сохранения импульса, либо закон сохранения момента импульса. Именно эти законы и составляют основу дифференциальных уравнений, наиболее востребованных при решении прикладных задач.
В общем виде эти уравнения можно записать как:
где \(\vec<<\rm\phi >>=\left(<\rm\phi >_ <1>,<\rm\phi >_ <2>. <\rm\phi >_
где \(H = H(x, t)\) — высота свободной границы жидкости над ровным дном, \(u=u\left(x,t\right)\) — скорость жидкости, \(g\)- ускорение свободного падения.
Первое из этих уравнений представляет собой закон сохранения массы, второе — закон сохранения импульса. Закон сохранения полной механической энергии \(E_
Уравнения газовой динамики (уравнения Эйлера) представляют собой законы сохранения массы, импульса и полной энергии:
Здесь \(<\rm\rho >\) — полная удельная энергия, \(e\)- удельная внутренняя энергии.
В случае нескольких пространственных изменений консервативная форма записи уравнений механики сплошных сред будет иметь вид:
В частности, в таком виде можно представить уравнения Навье — Стокса, уравнения динамической теории упругости, уравнения линейной и нелинейной акустики и оптики, уравнения Максвелла и многие другие.
Механика многофазных сред – наука и инженерные приложения 3 страница
II.4.2.5. Модель неньютоновских жидкостей
Определение. Жидкости, моделируемые условием 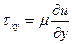
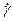
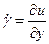
Пример. Модель степенной жидкости Оствальда
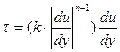
Здесь связь между τ в слоях жидкости степенная
Кажущаяся вязкость в среде –
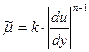
где k, n – коэффициенты в среде.
Определение. Если n 1 – среды – дилатантные (например, крахмальный клейстер).
Пример. Вязко-пластическая среда с предельным напряжением сдвига; модель “жидкости” Шведова-Бингама (сюда относятся высокопарафинистые и застывающие нефти, глинистые растворы, лаки, краски):
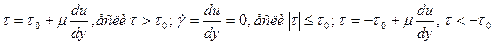
Физический смысл (6). Пока τ не превышает по mod некоторую предельную величину τ0 (является предельным напряжением сдвига), течение такой среды не начинается (в этом случае 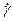
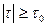
II.4.2.6. Модель упруго-деформируемого трубопровода
При схематизации процессов движения жидкостей и газов в трубопроводе используются модели трубопровода.
Модель недеформируемой трубы (МНТ), т.е. цилиндра с постоянными не изменяющимся внутренним диаметром d0 и постоянной толщиной δ стенки. Внешний диаметр D=d0 +2δ тоже остается постоянным.
При изучении гидравлического удара МНТ оказывается неточной в анализе явлений переноса В этих условиях используется модель упруго -деформируемого трубопровода (МУДТ).
Опыт показывает, что объем внутренней полости трубы хоть незначительно, но изменяется при изменении T, p среды. Поэтому для учета объемного расширения трубопровода при отклонении T от T0, имеем модель
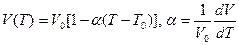
Здесь α – коэффициент объемного расширения металла, из которого сделан трубопровод. Существенно больше объем внутренней полости трубопровода изменяется от разности внутренного и внешнего давлений.
При одновременном отклонении p и T от p0 и T0 соответственно, используют модель
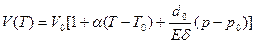
где E-модуль Юнга, δ – толщина стенки.
§ II.4.3. Уравнения движения и сплошности в однофазной области
Движение среды в любой области газожидкостной системы будет определяться уравнениями гидродинамики (Навье-Стоска):
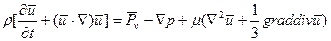
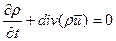
В обозначениях принято: 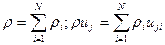
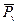
В случае многокомпонентной среды к (1), (2) добавляется уравнение диффузии индивидуальной компоненты:
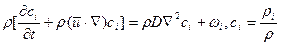
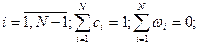
Для неизотермических условий к уравнениям (1)-(4) добавляются энергетические уравнения — теплопроводности Фурье-Кирхгоффа (5) или Фурье-Острроградского (6):
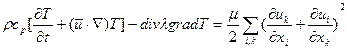
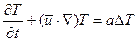
§ II.4.4. Механическое взаимодействие на границе раздела фаз
Для уравнений движения, написанных попарно для каждой из фазовых областей газожидкостной системы необходимо задать условия, связывающие поля давлений и скорости по поверхностям раздела фаз.
Выделим контрольной поверхностью F замкнутую область объема V, заключающую в себе часть поверхности раздела фаз, где F1 – поверхность тяжелого компонента — жидкость, F2 — поверхность легкого компонента – газ.
Считаем, что к поверхности F=F1+F2 приложены нормальные σ и касательные τ напряжения. Тогда условие динамического равновесия рассматриваемой области имеет вид:
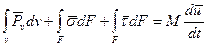
В (1) M — масса, заключенная в объеме V; 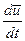
С другой стороны:
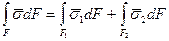
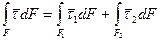
Стягивая поверхность F к заключенной в V поверхности раздела фаз Fгр, имеем:
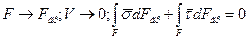
Вывод. Т.к. 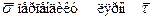
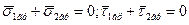
Замечание. Если прямоугольную систему координат расположить так, чтобы плоскость (xz) была касательной к поверхности раздела фаз в данной точке, а ось y нормальна к этой поверхности, то согласно уравнениям гидродинамики:
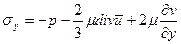
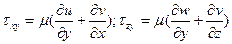
Условие отсутствия скольжения фаз на границе раздела:
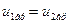
Нормальные к плоскости (xz) составляющие вектора скорости на границе раздела фаз определяются массовой скоростью фазового превращения 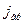
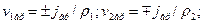
Замечание. 1. Если фазовые превращения отсутствуют, то 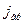
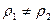
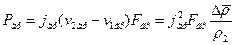
где 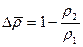
3. Если предположить, что qф — плотность теплового потока, идущего на испарение (конденсацию) на ПРФ, а скрытая теплота фазового превращения – r, то
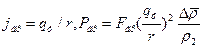
§ II.4.5. Тепловое взаимодействие на границе раздела фаз
Тепловой баланс объема V, включающего в себя ПРФ, имеет вид
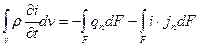
где 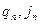
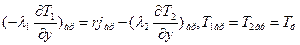
где 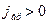
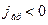
§ II.4.6. Скачок давления на границе раздела фаз
Т.к. молекулы жидкости, расположенные на ее границе с газом (твердым телом, другой жидкостью) находятся с силовом поле как остальных молекул своей среды, так и молекул другой среды, то силовое поле, действующее на поверхностный слой несимметрично. Поэтому возникает сила, направленная в сторону более плотной среды. Расстояние, на котором проявляется действие молекул, весьма мало. Молекулы поверхностного слоя имеют свободную энергию, которая изменяется при деформации ПРФ. Поскольку равновесие системы устойчиво при минимальной свободной энергии, то любая жидкость стремиться максимально сократить свою свободную поверхность. Отсюда жидкость, не подверженная действию односторонних сил, принимает форму сферы. Эти эффекты учитывает коэффициент поверхностного натяжения (КПН).
Введем этот коэффициент 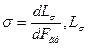
Определение. КПН – работа, которую необходимо совершить, чтобы увеличить ПРФ на единицу площади.
Замечание. Искривление ПРФ вызывает скачок давления, который определяется формулой Лапласа:
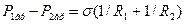
Здесь R1, R2 — главные радиусы кривизны ПРФ в данной точке.
Радиус кривизны — положительный, если направлен вглубь первой фазы. У сферы R1= R2= R, и соответственно давление в газовом потоке больше давления в окружающей жидкости на величину
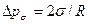
Замечание. Эффект поверхностного натяжения – давление насыщения также меняется с кривизной границы раздела фаз.
Приращение давления насыщения вследствие кривизны поверхности при одной и той же температуре определяется по формуле Кельвина
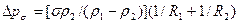
Глава II.5. Уравнения механики сплошных гетерогенных сред
§ II.5.1. Уравнения сохранения для составляющих
Запишем балансовые соотношения массы, импульса и энергии для каждой составляющей в некотором фиксированном объеме смеси V, ограниченной поверхностью S, учитывая, что имеется взаимодействие не только с внешней (по отношению к выделенному объему V) средой, но и соответствующий обмен массой, импульсом, энергией между составляющими внутри V.
II.5.1.1. Уравнение сохранения массы
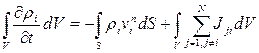
Здесь 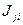
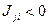
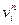
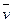
Из законов сохранения массы при различных физико-химических превращениях, имеем
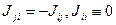
При переходе от поверхностного интеграла к объемному в (1) используется формула Гаусса-Остроградского:
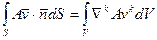
Применяя (3) к (1) имеем
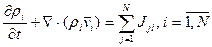
Здесь (4) – дифференциальное уравнение (ДУ) сохранения индивидуальной составляющей (i).
Уравнение (4) можно переписать, если использовать диффузионную скорость
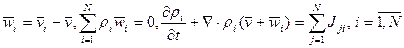
Замечание. Если просуммировать (4) или (5) по i, учитывая 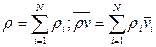

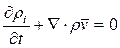
Вывод: уравнение неразрывности (6) в целом не чувствительно к относительному движению составляющих.
II.5.1.2. Уравнение импульсов
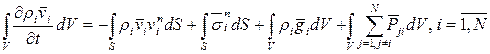
Физический смысл слагаемых правой части (7). ① — приток импульcа i-й составляющей через поверхность S; ②,③ — воздействие внешних поверхностных и массовых сил, приходящихся на i-ю составляющую и характеризуемых тензором 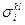
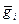
Из закона сохранения импульса при различных взаимодействиях
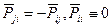
Применяя формулу Остроградского-Гаусса (3) к (7) имеем ДУ импульсов каждой составляющей:
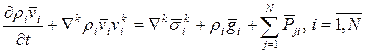
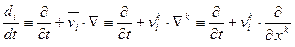
и уравнения (5) , имеем уравнение (9) в виде:
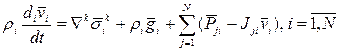
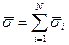
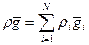
для сферы в целом, то суммируя (9) по i c учетом (12), имеем уравнение импульсов среды в целом:
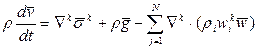
Замечание. Уравнение (13) в отличие от уравнения неразрывности (6), зависит от относительного движения составляющих.
II.5.1.3. Уравнение энергии
Замечание. Введем понятие удельной энергии смеси E (энергия приходящаяся на единицу массы среды) E=u+K, где u – внутренняя энергия, K – кинетическая энергия. В случае многофазной среды: внутренняя энергия смеси аддитивна по массе входящих в нее составляющих
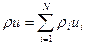
Здесь ui – удельные внутренние энергии составляющих смеси. Кинетическая энергия определяется макроскопическим движением
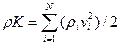
Тогда полная энергия смеси будет
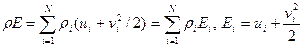
Из (15) и (5) для диффузионных скоростей (т.е. с использованием связи 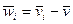
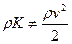
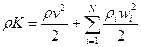
Из (16) видно, что кинетическая энергия многоскоростной среды определяется не только ее движением как целого со скоростью центра масс 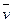
Балансовое уравнение для энергии каждой составляющей смеси в интегральной форме, имеет вид:
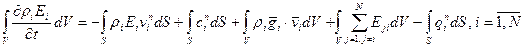
Замечание. (Физический смысл слагаемых правой части уравнения (18)):
I. ① — приток энергии i-й составляющей через S; ②,③ — работа внешних поверхностных сил [характеризуемая вектором 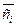
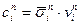
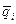
II. Для (18) справедливо: 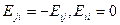
После применения формулы Гаусса-Остроградского (3) к уравнению (18) [используя уравнение неразрывности (4) –для перехода к индивидуальной компоненте ρi] следует ДУ энергии:
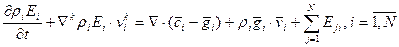
(20) – дивергентная форма ДУ. Бездивергентная форма ДУ полной энергии:
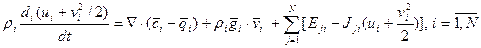
Суммируя по i уравнение (20) и учитывая (5), (6) (т.е. диффузионную скорость, уравнение неразрывности для смеси, соотношения (19) для Eji), получим уравнение энергии для смеси в целом:
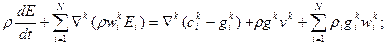
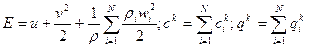
Вывод: уравнение энергии, как и уравнение импульсов (13), зависит от относительного движения составляющих.
Замечание (по обобщению понятия субстанциональной производной для величин, характеризующих смесь в целом и аддитивных величин по массам, входящих в смесь составляющих).
В отличие от обычной односкоростной СС, в данном случае понятие производной, дающей изменение параметра вдоль траектории выделенной частицы смеси, ее составляющие обладающие различными скоростями и траекториями, расходятся.
Так, в обычной односкоростной среде справедливо
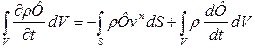
Для соотношения (24) имеем: 1. 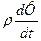
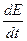
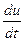
В случае многоскоростной среды выражение (24) допускает обобщение, определяющее 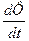
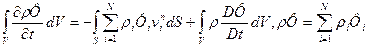
I. Введенная величина — 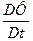
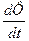
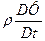
II. II. Из (25) следует выражение для 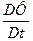
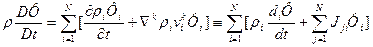
III. Из выражений для субстанциональной производной (10), а также соотношений (5), (16) следует выражение для формально определенной барицентрицеской субстанциональной производной:
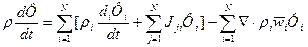
Таким образом, из (26), (27) видно отличие 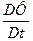
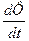
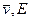
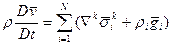
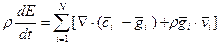
Уравнения (28), (29) – балансовые связи для скорости и энергии, могут быть использованы для описания любого многоскоростного континуума, соответствующей гомогенной и гетерогенной смеси.
§ II.5.2. Диффузионное приближение для гомогенных смесей
Определение. В гомогенной смеси, представляющей смесь газов, растворы, сплавы, ее составляющие, которые называются компонентами, размешаны и взаимодействуют на молекулярном или атомном уровне, скорости их относительного движения малы и их нужно учитывать в связи с определением концентраций компонент, и в то же время можно пренебречь динамическими и инерционными эффектами из-за относительного движения компонент.
Замечание. С формальной точки зрения при условии
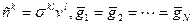
диффузионное приближение (в механике смесей) связано с пренебрежением слагаемыми, содержащими величины второго порядка относительно диффузионных скоростей 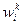
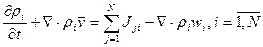
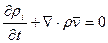
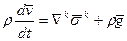
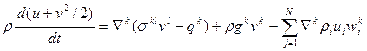
1. Уравнение реологии и состояния для всей среды в целом, задающие тензор напряжений 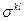
2. Считается, что тензор скоростей деформации 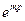
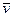
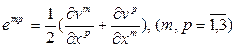
а влияние состава смеси непосредственно проявляется через физико-химические параметры, входящие в уравнение реологии и состояния
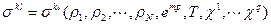
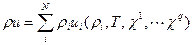
3. Относительные движения компонент, описываемые диффузионными скоростями или диффузионными потоками 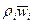
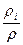
4. О законах диффузии. Устанавливаются зависимости, как правило, линейные для мгновенных значений 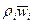
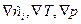
5. Модели, построенные на основе диффузионного приближения (1) для многоскоростного континуума фактически являются односкоростными, и поэтому диффузионное приближение называется одножидкостным.
6. Усложнение диффузионной теории смеси посредством учета температурных эффектов фактически не меняют существа диффузионного приближения, связанного: (i) с пренебрежением динамическими и инерционными эффектами относительного движения компонент; (ii) с применением законов диффузии для определения этого относительного движения.
§ II.5.3. Особенности математического описания гетерогенных смесей
Замечание. В отличие от ГоС ГеС, включающие газовзвеси, суспензии, эмульсии, пузырьковые жидкости, водонасыщенные грунты, углеводородные смеси, композитные материалы и т.д., описываются многоскоростной или многожидкостной моделью с учетом динамических эффектов из-за несовпадения скоростей составляющих, которые называются фазами. Это необходимо, т.к. скорости относительного движения фаз 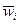
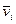
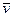
Система определяющих уравнений имеет вид:
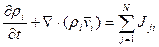
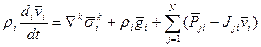
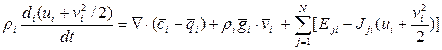
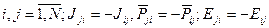
Замечание. (Отличие ГоС от ГеС).
I. В ГоС каждая компонента может рассматриваться как занимающая весь объем смеси равноправно с другими компонентами (V1 =V2=…=VN =V), в ГеС каждая фаза занимает лишь часть объема смеси (V1+ V1+…+VN =V). Для этой цели в теории ГеС используют величины αi (i=1…N), характеризующие доли объема смеси, занимаемой каждой фазой:
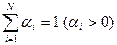
Вывод. Помимо приведенных плотностей ρi, вводятся истинные плотности вещества фаз 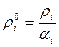
II. В ГеС необходимо учитывать, что фазы присутствуют в виде макроскопических (по отношению к молекулярным размерам) включений или в виде среды, окружающей эти включения, поэтому деформация любой фазы связана [для сравнения, в ГоС имеем 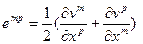
Дата добавления: 2017-01-29 ; просмотров: 1124 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Консервативные схемы
Для нелинейных уравнений и соответствующих им разностных схем трудно доказывать сходимость. Поэтому пользуются часто так называемым понятием практической сходимости. Она состоит в том, что расчеты по данной схеме проводят многократно на сгущающейся сетке. Сходимость к некоторому решению является подтверждением достоверности результатов. Однако такой способ годится только для гладких решений. При решении задач с разрывами сходимость решения к некоторому пределу при h→0 может оказаться ложной, а получаемое при этом решение — неверным.
Подобных ситуаций можно избежать путем использования консервативных разностных схем. Они основаны на дивергентной форме записи исходных уравнений. Поясним суть этой формы. При описании физических процессов исходные уравнения могут записываться в дифференциальной форме относительно искомых функций (например, плотности, давления, скорости и др.). Существует и другая форма записи уравнений, при которой искомыми параметрами являются масса, энергия, количество движения и т.п., а сами уравнения выражают законы сохранения этих параметров. Такая форма записи уравнений называется дивергентной.
Формально квазилинейное уравнение переноса (2.44) можно также записать в дивергентной форме:

Проинтегрируем это уравнение по ячейке

Здесь 
Аналогичное интегральное уравнение можно получить для всей расчетной области 


Уравнения (2.58) и (2.59) содержат лишь функции, относящиеся к границе соответственно ячейки и всей расчетной области. Эти уравнения можно трактовать как физические законы сохранения: сколько массы, энергии и т. д. в область через границу втекло, столько и вытекло. При этом, если просуммировать уравнение (2.58) по всем ячейкам, получается уравнение (2.59) для всей области. Таким образом, из законов сохранения по каждой ячейке следует закон сохранения для всей области. Схемы, не обладающие этим свойством, называются неконсервативными. При их суммировании по всем ячейкам появляется некоторая величина, называемая дисбалансом, которая приводит к нарушению закона сохранения для всей области.
В консервативных схемах дисбаланс равен нулю. Приведем пример построения такой схемы. Для этого нужно использовать некоторый численный метод вычисления интегралов, входящих в уравнение (2.58). Воспользуемся для простоты формулой прямоугольников, причем узлы интегрирования предполагаем совпадающими с узлами рассматриваемой разностной сетки. Окончательно получим разностную схему вида
Отсюда можно найти значение искомой функции на верхнем слое с помощью решения на нижнем слое. Следовательно, это явная схема. Она обладает свойством консервативности. Аналогичным образом, выбирая различные шаблоны, можно построить другие консервативные разностные схемы. Консервативные схемы дают результаты с хорошей точностью как для разрывных, так и непрерывных решений. Они оказались полезными при исследовании различных физических явлений. Конкретную схему для решения данной задачи выбирают с учетом требований этой задачи, предъявляемых к схеме (монотонность схемы, однородность, порядок аппроксимации и др.), которые часто бывают противоречивы. Выбранная схема должна быть испытана на решении тестовых задач.
http://helpiks.org/8-98613.html
http://3ys.ru/metody-resheniya-differentsialnykh-uravnenij/konservativnye-skhemy.html