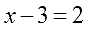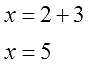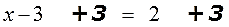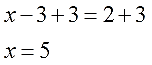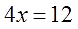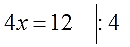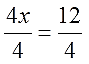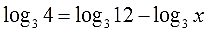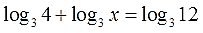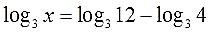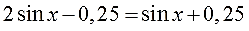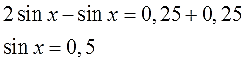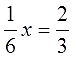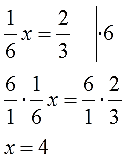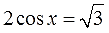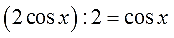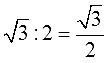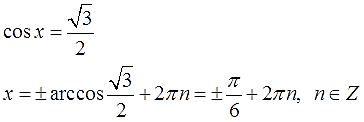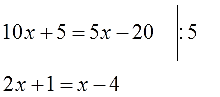Для чего нужно решать уравнения
Вот пример прямой задачи: сколько весит кусок сплава, на изготовление которого пошло 0,6 дм³ меди (уд. вес 8,9 кг / дм³) и 0,4 дм³ цинка (уд. вес 7,0 кг/ дм³)? При ее решении мы находим вес взятой меди (8,9 · 0,6 = 5,34 (кг)), затем вес цинка (7,0 · 0,4 = 2,8 (кг)) и, наконец, вес сплава (5,34 + 2,8 = 8,14 (кг)). Выполняемые действия и их последовательность диктуются самим условием задачи.
Вот пример косвенной задачи: кусок сплава меди и цинка объемом в 1 дм³ весит 8,14 кг. Найти объемные количества меди и цинка в этом сплаве. Здесь из условия задачи не видно, какие действия ведут к ее решению. При так называемом арифметическом решении нужно проявить подчас большую изобретательность, чтобы наметить план решения косвенной задачи. Каждая новая задача требует создания нового плана. Труд вычислителя затрачивается нерационально. Для рационализации вычислительного процесса и был создан метод уравнений, который является основным предметом изучения в алгебре. Суть этого метода такова.
1.Искомые величины получают особые наименования. Мы пользуемся для этой цели буквенными знаками (предпочтительно последними буквами латинского алфавита х, у, z, u, v). Условие задачи с помощью этих знаков и знаков действий (+, — и т. д.) «переводится на математический язык», т. е. связи между данными и искомыми величинами мы выражаем не словами и фразами разговорного языка, а математическими знаками. Каждая такая «математическая фраза» и есть уравнение.
2.После этого мы решаем уравнение, т. е. находим значения искомых неизвестных величин. Решение уравнения производится совершенно механически, по общим правилам. Нам не приходится больше учитывать особенности данной задачи; мы только должны применять раз навсегда установленные правила и приемы. (Выводом этих правил и занимается в первую очередь алгебра.)
Таким образом, уравнения нужны для того, чтобы механизировать труд вычислителя. После того как уравнение составлено, решение его можно получить вполне автоматически (в настоящее время сконструирован ряд таких автоматов). Вся трудность решения задачи сводится лишь к составлению уравнения.
Что такое уравнение? Как решать уравнения?
Уравнение — одно из краеугольных понятий всей математики. Как школьной, так и высшей. Имеет смысл разобраться, правда? Тем более, что это очень простое понятие. Ниже сами убедитесь. 🙂 Так что же такое уравнение?
То, что это слово однокоренное со словами «равный», «равенство», возражений, думаю, ни у кого не вызывает.
Уравнение — это два математических выражения, соединённых между собой знаком «=» (равно).
Но… не каких попало. А таких, в которых (хотя бы в одном) содержится неизвестная величина. Или, по-другому, переменная величина. Или, сокращённо, просто «переменная». Которая обычно обозначается буквой «х».
Переменных может быть одна, может быть несколько. В школьной математике чаще всего рассматриваются уравнения с одной переменной. И мы тоже пока что будем рассматривать уравнения с одной переменной. С двумя переменными или более — в специальных уроках.
Что значит решить уравнение?
Переменная, входящая в уравнение, может принимать любые допустимые математикой значения. На то она и переменная. 🙂 При каких-то значениях переменной получается верное числовое равенство, а при каких-то — нет.
Решить уравнение означает найти ВСЕ такие значения переменной, при подстановке которых в исходное уравнение получается верное равенство. Или, более научно, верное тождество. Или доказать, что таких значений переменной не существует.
Что такое верное равенство? Это равенство, не вызывающее сомнений даже у человека, абсолютно не отягощённого глубокими математическими познаниями. Например, 5=5, 0=0, -10=-10. И так далее. 🙂
Значения переменной, при подстановке которых достигается это самое верное равенство, называются очень красиво и научно — корни уравнения.
Корень может быть один, может быть несколько. А может быть и бесконечно много корней — целый интервал или даже вообще вся числовая прямая от –∞ до +∞. Да, такое тоже бывает! Всё от конкретного уравнения зависит.)
А бывает и такое, что нельзя найти такие иксы, которые давали бы нам верное равенство. Принципиально нельзя. По определённым причинам. Нету таких иксов…
В таких случаях обычно говорят, что уравнение не имеет корней.
Для чего нужны уравнения?
Вопрос смешной. Для жизни! В школе, как правило, уравнения нужны для решения текстовых задач. Это, напоминаю, задачи на движение, на работу, на проценты и многие другие.
А во взрослой жизни без уравнений невозможны было бы ответить даже на самые обычные, но жизненно важные вопросы повседневности: какая будет погода завтра, выдержит ли заданную нагрузку здание. Или лифт. Или самолёт. Куда попадёт ракета… И не было бы сейчас среди нас ни синоптиков, ни инженеров, ни бухгалтеров, ни экономистов, ни программистов… За ненадобностью. Внушает?)
Почему это так? А потому, что уравнениями описываются почти все известные человеку природные явления и процессы. Изменение давления и температуры воздуха с высотой, закон всемирного тяготения, размножение бактерий, радиоактивный распад, химические реакции, электричество, спрос и предложение — в основе всего этого лежат математические уравнения! Простые, сложные — всякие. Какое явление или ситуация, такое и уравнение.)
Уравнения — очень мощный и универсальный инструмент для решения самых разных прикладных задач.
А какие бывают уравнения?
Уравнений в математике несметное количество. Самых разных видов. Но всё многообразие уравнений можно условно разделить всего на 4 категории:
3. Дробные (или дробно-рациональные),
Разные категории уравнений требуют и разного подхода к их решению: линейные уравнения решаются одним способом, квадратные — другим, дробные — третьим, тригонометрические, логарифмические, показательные и прочие — тоже решаются своими методами.
Прочих уравнений, разумеется, больше всего, да…) Это и иррациональные, и тригонометрические, и показательные, и логарифмические, и многие другие уравнения. И даже дифференциальные уравнения (для студентов), где роль неизвестного играет не число, а функция. Или даже семейство функций. 🙂
В соответствующих уроках мы подробно разберём все эти типы уравнений. А здесь у нас — базовые приёмы и правила.
Называются эти правила — тождественные (или — равносильные) преобразования уравнений. Их всего два. И нигде их не обойти. Так что знакомимся!
Как решать уравнения? Тождественные (равносильные) преобразования уравнений.
Решение любого уравнения заключается в поэтапном преобразовании входящих в него выражений. Но преобразований не абы каких, а таких, чтобы от шага к шагу суть всего уравнения не менялась. Несмотря на то, что после каждого преобразования уравнение будет видоизменяться и, в конечном счёте, станет совсем не похоже на исходное.
Такие преобразования в математике называются равносильными или тождественными. Их довольно много, но среди всего многообразия тождественных преобразований уравнений выделяется два базовых. О них и пойдёт речь в этом уроке. Да-да, всего два! Но — крайне важных! И каждое из них заслуживает отдельного внимания.
Применение этих двух тождественных преобразований в том или ином порядке гарантирует успех в решении 99% уравнений математики. Заманчиво, правда?
Первое тождественное преобразование:
К обеим частям уравнения можно прибавить (или отнять) любое (но одинаковое!) число или выражение (в том числе и с переменной). Суть уравнения от этого не изменится.
Это преобразование вы применяете всюду, наивно думая, что переносите какие-то члены из одной части уравнения в другую, меняя знаки. 🙂
Например, такое крутое уравнение:
Тут и думать нечего, перебрасываем тройку вправо, меняя минус на плюс:
А что же происходит в действительности? А на самом деле вы… прибавляете к обеим частям уравнения тройку!
Вот что у вас происходит:
И результат получается тем же самым:
Вот и всё. Слева остаётся чистый икс (чего мы, собственно, и добиваемся), а справа — что уж получится. Но самое главное то, что от прибавления тройки к обеим частям суть всего уравнения не изменилась!
Дело в том, что привычный нам перенос слагаемых из одной части в другую со сменой знака — это просто сокращённый вариант первого тождественного преобразования.
И зачем нам так глубоко копать? В уравнениях — незачем. Переносите себе спокойно и не парьтесь. Только знаки менять не забывайте.) А вот в неравенствах привычка к переносу может и слегка обескуражить, да…
Это было первое тождественное преобразование. Переходим ко второму.
Второе тождественное преобразование:
Обе части уравнения можно умножить (разделить) на одно и то же отличное от нуля число или выражение.
Это тождественное преобразование мы вы постоянно применяете, когда решаете что-нибудь совсем уж жуткое типа:
Тут каждому ясно, что х=3. А вот как вы получили этот ответ? Подобрали? Угадали?
Чтобы не подбирать и не гадать (мы с вами математики, а не гадалки), нужно понять, что вы просто поделили обе части уравнения на четвёрку. Которая нам и мешает.
Эта палка с делением означает, что на четвёрку делятся обе части нашего уравнения. Через дроби эта процедура выглядит так:
Слева четвёрки благополучно сокращаются, остаётся икс в гордом одиночестве. А справа при делении 12 на 4 получается, понятное дело, тройка. 🙂
Звучит невероятно, но эти два (всего два!) простых преобразования лежат в основе решения всех уравнений математики! Да-да, именно всех, я нисколько не преувеличиваю! От линейных и квадратных в школе до дифференциальных в ВУЗе.)
Ну что, посмотрим на тождественные преобразования уравнений в действии?
Применение тождественных преобразований к решению уравнений.
Начнём с первого тождественного преобразования. Переноса вправо-влево.
Пример для новичков:
Дело нехитрое. Это линейное уравнение. Работаем прямо по заклинанию: «С иксами влево, без иксов — вправо».
Эта мантра — универсальная инструкция по применению первого тождественного преобразования. Вот и смотрим на уравнение. Какое слагаемое с иксом у нас справа? Что? 2х? Не-а!) Справа у нас -2х (минус два икс)! Поэтому при переносе в левую часть минус поменяется на плюс:
1 — х +2х = 3
Полдела сделано, иксы собрали слева. Осталось все числа собрать справа. Слева в уравнении стоит единичка. Опять вопрос — с каким знаком? Ответ «с никаким» не катит.) Слева перед единицей и вправду ничего не написано. А это значит, что перед ней стоит знак «плюс». Так уж в математике повелось: ничего не написано — значит, плюс.)
И поэтому вправо единичка перенесётся уже с минусом:
-х + 2х = 3 — 1
Вот почти и всё. Слева приводим подобные, а справа — считаем. И получаем:
Это было совсем примитивное уравнение.
Теперь пример покруче, для старшеклассников:
Уравнение логарифмическое. Ну и что? Какая разница? Всё равно первым шагом делаем базовое тождественное преобразование («С иксами влево ….»). Для этого слагаемое с иксом (то есть, —log3x) переносим влево. Со сменой знака:
А числовое выражение (log34) переносим вправо. Также со сменой знака, разумеется:
Вот и всё. Справа получилась чистая формула. Кто дружит с логарифмами, тот в уме дорешает уравнение и получит:
Что? Хотите синусы? Пожалуйста, вот вам синусы:
И снова всё то же самое! Выполняем первое тождественное преобразование — переносим sin x влево (с минусом), а -0,25 переносим вправо (с плюсом):
Получили простейшее тригонометрическое уравнение с синусом, решить которое (для знающих) также не составляет никакого труда.
Видите, насколько универсально первое равносильное преобразование! Встречается везде и всюду и не обойти его никак… Именно поэтому так важно уметь его делать на автомате и без ошибок.
Собственно, ошибиться здесь можно лишь в одном — забыть сменить знак при переносе. Что и происходит сплошь и рядом. Внимательность никто не отменял, да…)
Ну что, продолжаем наши игры? Развлекаемся теперь со вторым преобразованием!)
Крутяк, прямо скажем.) Ладно, это эмоции…
Смотрим и соображаем: что нам мешает в этом уравнении? Что-что… Да семёрка мешает! Хорошо бы от неё избавиться. Да так, чтобы исходное уравнение не испортить.)
Но как? Перенести вправо? Ээээ… Стоп! Нельзя.) Семёрка с иксом умножением связана. Коэффициент, видите ли.) Нельзя её оторвать от икса и вправо перенести. Вот всё выражение 7х целиком — пожалуйста (вопрос — зачем?). А семёрку отдельно — никак нет.
Самое время про умножение/деление вспомнить! Нам ведь в ответе чистый икс нужен, не так ли? А семёрка — мешает. Вот и делим левую часть на семь. «Очищаем» икс от коэффициента. Так нам надо. Но тогда и правую часть тоже надо поделить на семь: этого уже математика требует. Что уж там получится, то и получится. Но пример хороший. Я старался.) 28 на 7 замечательно делится. Получится 4.
Или такое уравнение:
Что здесь нам мешает? Дробь 1/6, не так ли? Вот давайте и избавимся от неё. Безопасно для уравнения.) Как? Ну, можно поступить аналогично — поделить обе части на эту самую 1/6. Но в уме это не очень удобно. Кое-кто и запутается…
Но мы же не только делить, мы ещё и умножать умеем!) Вспоминаем из младших классов, после какого действия у нас пропадает дробь? Правильно! Дробь у нас пропадает при умножении на число, равное (или кратное) её знаменателю. Вот и умножим обе части нашего уравнения на 6. Слева всё равно чистый икс получится, а умножение правой части на 6 — не самая трудная работа.)
Вот и всё.) Умножение обеих частей уравнения на нужное число позволяет сразу избавляться от дробей, минуя промежуточные выкладки, в которых, между прочим, запросто можно и ошибок наляпать. Короче дорога — меньше ошибок!
Теперь снова на машину времени и — в старшие классы:
Чтобы добраться до икса и тем самым решить это крутое тригонометрическое уравнение, нам надо сначала получить слева чистый косинус, безо всяких коэффициентов. А двойка мешает. 🙂 Вот и делим на 2 всю левую часть:
Но тогда и правую часть тоже придётся разделить на двойку: это уже МАТЕМАТИКЕ надо. Делим:
Получили справа табличное значение косинуса. И теперь уравнение решается за милую душу.)
Вот и вся премудрость. Как видите, тождественные преобразования уравнений — штука полезная. И при этом не самая сложная. Перенос да умножение/деление. Однако далеко не у всех они получаются с первого раза и без ошибок, ох не у всех… Основные проблемы здесь две.
Проблема первая (для малоопытных):
Иногда ученик думает, что упрощение уравнений делается по одному, раз и навсегда установленному правилу. И никак не может уловить и понять это правило: в каких-то примерах начинают с домножения (или деления), в каких-то — с переноса. Где-то три раза переносят и ни разу не домножают…
Например, такое линейное уравнение:
С чего начинать? Можно начать с переноса:
А можно сначала поделить обе части на пятёрку, а затем уж переносить. Тогда сразу числа попроще станут:
Как видим, и так и сяк решать можно. И это — в примитивном примере! Вот и возникает у неопытных учеников вопрос: «Как правильно?»
По-всякому правильно! Кому как удобнее. 🙂 Универсального рецепта здесь нет и быть не может. Математика предлагает вам на выбор два вида преобразований уравнений. А порядок этих самых преобразований зависит исключительно от исходного уравнения, а также от личных предпочтений и привычек решающего.
Проблема вторая (для всех…ну… почти):
Ошибки в вычислениях. В преобразованиях постоянно приходится перемножать скобки. Заключать выражения в скобки и раскрывать скобки. Умножать и делить дроби. Работать со степенями… Короче, в наличии весь набор элементарных действий математики. Со всеми вытекающими…
Обе эти проблемы устраняются только одним способом — практикой. Исчезают сомнения и ошибки. Примеры становятся проще, задания — легче. И в итоге не математика командует вами, а вы — математикой. 🙂
Решение простых линейных уравнений
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа. Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Числовой коэффициент — число, которое стоит при неизвестной переменной.
Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Как решать простые уравнения
Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.
Для примера рассмотрим простейшее уравнение: x+3=5
Начнем с того, что в каждом уравнении есть левая и правая часть.
Перенесем 3 из левой части в правую и меняем знак на противоположный.
Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.
Приведем подобные и завершим решение.
2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.
Применим правило при решении примера: 4x=8.
При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.
Разделим каждую часть на 4. Как это выглядит:
Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:
Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12
- Разделим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.
−4x = 12 | : (−4)
x = −3
Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.
Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.
| Алгоритм решения простого линейного уравнения |
|---|
|
Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.
Примеры линейных уравнений
Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
- Перенести 1 из левой части в правую со знаком минус.
Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.
Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1.
5х − 15 + 2 = 3х − 12 + 2х − 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.
5х − 3х − 2х = −12 − 1 + 15 − 2
Приведем подобные члены.
Ответ: х — любое число.
Пример 3. Решить: 4х = 1/8.
- Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.
Пример 4. Решить: 4(х + 2) = 6 − 7х.
- 4х + 8 = 6 − 7х
- 4х + 7х = 6 − 8
- 11х = −2
- х = −2 : 11
- х = −2/11
Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.
Пример 5. Решить:
- 3(3х — 4) = 4 · 7х + 24
- 9х — 12 = 28х + 24
- 9х — 28х = 24 + 12
- -19х = 36
- х = 36 : (-19)
- х = — 36/19
Пример 6. Как решить линейное уравнение: х + 7 = х + 4.
5х — 15 + 2 = 3х — 2 + 2х — 1
Сгруппировать в левой части неизвестные члены, в правой — свободные члены:
Приведем подобные члены.
Ответ: нет решений.
Пример 7. Решить: 2(х + 3) = 5 − 7х.
http://abudnikov.ru/shkolnikam/uravneniya/chto-takoe-uravnenie-kak-reshat-uravneniya.html
http://skysmart.ru/articles/mathematic/reshenie-prostyh-linejnyh-uravnenij