Для чего нужно уметь решать квадратные уравнения

Роль и место квадратных уравнений в образовательном процессе школьников

2014г. ученица 9 Б класса

Тема: «Роль и место квадратных уравнений в образовательном процессе школьников»

(проблемно –исследовательская работа)

Скачать:

Предварительный просмотр:

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №9 г. Холмска

муниципального образования «Холмский городской округ»

Тема: «Роль и место квадратных уравнений в образовательном процессе школьников»

(проблемно –исследовательская работа)

ученица 9-б класса

Руководитель: учитель математики

Глава 1.История квадратных уравнений. 5

Глава 2.Математичская модель — квадратные уравнения и его корни. 8

1. Неполное квадратное уравнение; 8
2. Метод выделения полного квадрата; 8
3. Решение квадратных уравнений по формуле; 9
4. Теорема Виета; 10
5. Биквадратные уравнения. 11

Глава 3.Приёмы устного решения квадратного уравнения. 12

3.1 Свойства коэффициентов квадратного уравнения; 12

3.2 Приём «Переброски». 13

Глава 4.Квадратные уравнения в предметах естественно-математического цикла. 14

Глава 5.Комплексные числа. 15

Список литературы. 17

Ресурсы Интернета. 17

« Мне приходилось делить свое время между политикой и уравнениями . однако уравнения, по –моему, гораздо важнее, потому что политика существует только для данного момента, а уравнения будут существовать вечно.»

Школьник начальных классов, только приступивший к изучению арифметики, скажет, что математика изучает правила счёта предметов, школьники постарше добавит к сказанному, что в понятие математики входят алгебра и геометрия, а выпускники средней школы включат в определение математики ещё изучение тригонометрии, вычисление производных и интеграла.

Любой восьмиклассник нашей школы особенно выделит, что математика изучает квадратные уравнения.

После изучения темы: Квадратные уравнения» наша учительница по математике Л.И. Рязанцева проводит урок- отчёт. И вот какое стихотворение написал один из её учеников:

Квадратным уравнениям посвящается

Ах, уравнения, квадратные,

вы такие разные – распрекрасные

полные, неполные, приведенные.

Коэффициент у вас буквы латинские –

а, в и с величаемы.

И пути решения у всех разные –

разложи, перенеси, дискриминант найди.

А дискриминант в² — 4ас формула особая,

к полному и приведённом уравнению

Ах, уравнения, квадратные,

вы такие разные и корней у вас

количество разное – от двух корней

до пустого множества.

Квадратные уравнения – это математическая модель, которая позволят передать особенности изучаемого явления, ситуации.

Математическая модель — приближённое описание какого-либо класса явлений внешнего мира, выраженное с помощью математической символики. Математ и ческая мод е ль — мощный метод познания внешнего мира, а также прогнозирования и управления.

Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении многих текстовых задач, при решении неравенств второй степени и дробно- рациональных, при решении биквадратных, тригонометрических, показательных, иррациональных уравнений. Решение многих задач физики сводится к решению алгебраических и квадратных уравнений.

В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения.

Однако имеются и другие приёмы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения.

Данные приёмы решения заслуживают внимания, поскольку они не отражены в школьных учебниках математики.

Овладение данными приёмами поможет мне экономить время и эффективно решать уравнения. Потребность в быстром решении обусловлена применением тестовой системы итоговых экзаменов в 9 и 11 классах.

Я провела опрос старшеклассников:

1. Умеете вы решать квадратное уравнение?

8-б да! недавно изучали, 100%

1. Где применяются решения квадратных уравнений?

8-б – при решении задач из учебника.

9-б – при решении текстовых задач; при нахождении нулей квадратичной функции; при разложении квадратного трёхчлена на множители;

при решении квадратных неравенств;

при решении биквадратных уравнений;

при решении алгебраических уравнений, сводящихся к квадратным.

11-а – очень часто на уроках математики — при решении тригонометрических, показательных, логарифмических, иррациональных уравнений и неравенств;

при исследовании функций с помощью производной;

при нахождении пределов интегрирования;

на уроках физики.

1. Используешь ли ты при решении уравнений свойства коэффициентов?

Знакомясь с содержанием и структурой диагностических тестов ГИА, я подсчитала, что в среднем 23% всех заданий требуют умения решать квадратные уравнения.

Поэтому меня и заинтересовала эта тема.

1. Познакомиться с историей возникновения квадратных уравнений

2. Рассмотреть способы решения квадратных уравнений: метод выделения полного квадрата, решение квадратных уравнений по формуле, теорема Виета.

3.Изучить приёмы устного решения квадратного уравнения.

4.Узнать на уроках каких предметов задачи решаются с помощью квадратных уравнений.

5. Изучить структуру и содержание КИМ ГИА.

Гипотеза: знания различных способов решения квадратных уравнений и приёмов устного решения квадратных уравнений способствует быстрому и правильному решению задач и экономит время.

Задачи: Квадратные уравнения – это математическая модель реальности и её применение в школьном образовании.

Глава 1. История квадратных уравнений.

Квадратные уравнения в Древнем Вавилоне.

Необходимость решать уравнения не только первой, но и второй степени ещё в древности была вызвана потребность решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет назад до н. э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:

Правило решения этих уравнений, изложено в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты переводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.

Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

Как составлял и решал Диофант квадратные уравнения.

В “Арифметике” Диофант нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.

При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.

Вот, к примеру, одна из его задач.

Задача 11. “Найти два числа, зная, что их сумма равна 20, а произведение – 96” .

Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т. е. 10 – x. Разность между ними 2x. Отсюда уравнение

(10 + x) (10 – x) = 96,

Отсюда x = 2. Одно из искомых чисел равно 12, другое 8. Решение x = -2 для Диофанта не существует, так как греческая математика знала только положительные числа.

Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения.

y² – 20y + 96 = 0 (2)

Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удаётся свести задачу к решению не полного квадратного уравнения(1).

Квадратные уравнения в Индии

Задачи на квадратные уравнения встречаются уже в 499г. В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее:

« Как солнце блеском своим затмевает звёзды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи».

Одна из задач знаменитого индийского математика XIIв. Бхаскары:

Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений. Часть страницы из алгебры Бхаскары (вычисление корней).

Квадратные уравнения у ал-Хорезми

В алгебраическом трактате ал-Хорезми даётся классификация линейных уравнений и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:

1) “Квадраты равны корнями”, т. е. ax² = bx.

2) “Квадраты равны числу”, т. е. ax²= c.

3) “Корни равны числу”, т. е. ax = c

4) “Квадраты и числа равны корням”, т. е. ax² + c = bx/

5) “Квадраты и корни равны числу”, т. е. ax² + bx = c.

6) “Корни и числа равны квадратам”, т. е. bx + c + ax²

Для ал-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приёмами ал-джабар и ал-мукабала. Его решения, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида ал-Хорезми, как и все математики до 17 века, не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений ал-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.

Квадратные уравнения в Европе XIII — XVIIв.в.

Формулы решения квадратных уравнений по образцу ал-Хорезми в Европе были впервые изложены в книге “Книге абака”, написанной в 1202 г. Итальянским математиком Леонардо Фибоначчи. Этот объёмистый труд, в котором отражено влияние математики как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические примеры задач и первый в Европе подошёл к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других стран Европы. Многие задачи из “Книги абака” переходили почти во все европейские учебники 16 – 17 веков и частично 18 века. Общее правило решения квадратных уравнений, приведённых к единому каноническому виду: x² + bx = c,

при всевозможных комбинациях знаков коэффициентов b, c было сформулировано в Европе лишь в 1544 г. М.Штифелем.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в 16 веке учитывают, помимо положительных, и отрицательные корни. Лишь в 17 веке благодаря трудам Жирара, Декарта, Ньютона и других учёных способов решения квадратных уравнений принимает современный вид.

Квадратные уравнения – это математическая модель, которая позволят передать особенности изучаемого явления, реальной ситуации.

2.1 Квадратные уравнения и его корни

Квадратным уравнением называется уравнение ах² + bх + с = 0, где а≠0, а, b,с – заданные числа числа, х – неизвестное.

Коэффициенты а, b,с квадратного уравнения называют так: а- первым или старшим коэффициентом, b-вторым коэффициентом, с-свободным членом.

Неполное квадратное уравнение

Квадратное уравнение ах² + bх + с = 0 называют неполным , если хотя бы один из коэффициентов b или с равен нулю.

2) ах² + с = 0, ах² = -с

1. если с>0 , то нет действительных корней

2. если с , то х²= -с/а

2.2 Метод выделения полного квадрата

Пример1: решить квадратное уравнение

• Преобразуем это уравнение так:

Следовательно, х+1=2 или х+1= -2, откуда х1=1, х2= -3.

Решая уравнение, мы преобразовали его так, что в левой части получился квадрат двучлена, а правая часть не содержит неизвестное.

2.3 Решение квадратных уравнений по формуле.

Если D , то уравнение не имеет действительных корней

Пример1: х² — 4х +5 =0

D , то уравнение не имеет действительных корней

Пример2: 2х² + 3х + 1 = 0

«Виет – творец математической формулы.»

«Французский геометр Виет был выше всех своих современников. Он прославился обобщением алгебры и сделал несколько важных открытий в этой отрасли человеческих знаний.»

Решение уравнений с использованием теоремы Виета.

Как известно, приведенное квадратное уравнение имеет вид

х 2 + px + c = 0. (1)

Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид

x 1 x 2 = q,

Т.е., сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).

а) Если сводный член q приведенного уравнения (1) положителен ( q > 0 ), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p . Если р , то оба корня отрицательны, если р , то оба корня положительны.

x 2 – 3x + 2 = 0; x 1 = 2 и x 2 = 1, так как q = 2 > 0 и p = — 3

x 2 + 8x + 7 = 0; x 1 = — 7 и x 2 = — 1, так как q = 7 > 0 и p= 8 > 0.

б) Если свободный член q приведенного уравнения (1) отрицателен ( q ), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p , или отрицателен, если p > 0 .

x 2 + 4x – 5 = 0; x 1 = — 5 и x 2 = 1, так как q= — 5 и p = 4 > 0;

x 2 – 8x – 9 = 0; x 1 = 9 и x 2 = — 1, так как q = — 9 и p = — 8

Пример1: х² — 14х – 15 =0

Теорема Виета для полного квадратного уравнения:

По праву достойна в стихах быть воспета

О свойствах корней теорема Виета.

Что лучше, скажи, постоянства такого:

Умножишь ты корни – и дробь уж готова?

В числителе с, в знаменателе а.

А сумма корней тоже дроби равна.

Хоть с минусом дробь, что за беда.

В числителе в, b знаменателе а.

2.5 Биквадратные уравнения.

Биквадратным уравнением — называется уравнение вида ax 4 + bx 2 + c = 0 .

Биквадратное уравнение приводится к квадратному уравнению при помощи подстановки .

Новое квадратное уравнение относительно переменной :

Решая это уравнение, мы получаем корни квадратного уравнения и . Решая эти два уравнения ( и ) относительно переменной , мы получаем корни данного биквадратного уравнения.

Алгоритм решения биквадратных уравнений :

1. Ввести новую переменную
2. Подставить данную переменную в исходное уравнение
3. Решить квадратное уравнение относительно новой переменной
4. После нахождения корней ( ) подставить их в нашу переменную и найти исходные корни биквадратного уравнения

Решим биквадратное уравнение . Сначала приводим это уравнение к квадратному. Для этого введем вспомогательное неизвестное такое, что . Тогда . Теперь данное биквадратное уравнение приводится к виду:

Решая это квадратное уравнение, мы получим , . Так как , то данное биквадратное уравнение эквивалентно системе двух уравнений:

Решим каждое из этих уравнений и найдем объединение множеств их решений.

Глава 3. Приёмы устного решения квадратного уравнения.

1. Свойства коэффициентов квадратного уравнения:

Пусть дано квадратное уравнение ах 2 + bх + с = 0, где а ≠ 0.

1) Если, а + b + с = 0 (т.е. сумма коэффициентов равна нулю), то х 1 = 1,

Доказательство: Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение

x 2 + b/a • x + c/a = 0.

Согласно теореме Виета

По условию а – b + с = 0, откуда b = а + с. Таким образом,

x 1 + x 2 = — а + b/a= -1 – c/a,

x 1 x 2 = — 1• ( — c/a),

т.е. х 1 = -1 и х 2 = c/a, что и требовалось доказать.

1)Решим уравнение 345х 2 – 137х – 208 = 0.

Решение. Так как, а + b + с = 0 (345 – 137 – 208 = 0), то

х 1 = 1, х 2 = c/a = -208/345.

2)Решим уравнение 132х 2 – 247х + 115 = 0.

Решение. Так как, а + b + с = 0 (132 – 247 + 115 = 0), то

х 1 = 1, х 2 = c/a = 115/132.

3)Решим уравнение 5х 2 – 8х + 3 = 0.

Решение. Так как 5 – 8 + 3 = 0, то х 1 = 1; х 2 = 0,6.

Если в квадратном уравнении ах² + bх + с = 0 выполняется равенство а + с = в, то х1 = -1; х2 = — с/а.

1) 5х 2 – 8х + 3 = 0.

Так как 5 – 8 + 3 = 0, то х 1 = 1; х 2 = 0,6.

2) Решить уравнения с большими коэффициентами :

1) 319х² + 1988x + 1669 = 0.

х 1 = — 1; х 2 = -1669/319.

2) 839х² – 448x – 391 = 0.

х 1 = 1; х 2 = -391/839.

3) 939х² + 978x + 39 = 0.

х 1 = — 1; х 2 = -39/939.

3.2 Приём «Переброски»

Рассмотрим квадратное уравнение

ах 2 + bх + с = 0, где а ≠ 0.

Умножая обе его части на а, получаем уравнение

а 2 х 2 + аbх + ас = 0.

Пусть ах = у , откуда х = у/а ; тогда приходим к уравнению

равносильно данному. Его корни у 1 и у 2 найдем с помощью теоремы Виета.

Окончательно получаем х 1 = у 1 /а и х 1 = у 2 /а . При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски» . Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

1) Решим уравнение 2х 2 – 11х + 15 = 0.

Решение . «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение

у 2 – 11у + 30 = 0.

Согласно теореме Виета:

у 1 = 5 х 1 = 5/2 x 1 = 2,5

у 2 = 6 x 2 = 6/2 x 2 = 3.

2) Решим уравнение 6х² — 7х – 3 = 0

Глава 4. Квадратные уравнения в предметах естественно-математического цикла .

Задача 1. Вертикально вверх с начальной скоростью 7 м/с брошен камень. Через некоторое время =0,41 с после этого брошен вертикально вверх другой камень с такой же скоростью. На какой высоте (от земли ) встретятся камни?

Решение: Необходимо составить уравнения движения для обоих тел. После чего объединить их и решить. Движение равноускоренное вдоль прямой, поэтому векторы не нужны и сразу пишем уравнения движения в скалярной форме. Ось координат направим вверх, тогда для скорости

V1 = V01 — g * t (поскольку начальная скорость направлена против силы тяжести.)

откуда для координаты

Х1 = Х01 + V01 * t — g * t * t / 2

для второго тела выпущенного в момент времени t1 = t + dt уравнение движения будет иметь вид

Х2 = Х02 + V02 * (t + dt) — g * (t + dt) * (t + dt) / 2

При встрече тел их координаты совпадут, что на языке математики запишется как

Х01 + V01 * t — g * t * t / 2 = Х02 + V02 * (t + dt) — g * (t + dt) * (t + dt) / 2

поскольку тела запускаются из одной и той же точки и с одной и той же скоростью, то

Х01 = Х02 и V01 = V02

и окончательно уравнение принимает вид

V0 * t — g * t * t / 2 = V0 * (t + dt) — g * (t + dt) * (t + dt) / 2

У полученного квадратного уравнения относительно t может быть два, одно или ни одного решения. Нас будут интересовать решения с t > 0. Решения с t

Задача 2. Груз свободно падает с высоты 500 метров. Какое расстояние преодолевает груз за последнюю секунду своего падения?

Решение: Потенциальная энергия переходит в кинетическую

v = корень квадратный(2*g*h) — это скорость в момент удара

Рассмотрим обратный процесс примем скорость v за начальную при движении вверх, тогда пройденный путь s=v*t-g*t^2/2.

Так как t=1, то s=v-g/2 = корень квадратный(2*g*h) -g/2 = 100-5=95 метров

Задача 3. Ускорение свободного падения на Земле равно 10 м/с. Какой продолжительности должны быть сутки, чтобы тела на экваторе были невесомы?

Решение: Центростремительное ускорение есть v^2/R и оно же должно равняться ускорению свободного падения g

отсюда следует, что линейная скорость точки на экваторе должна быть

далее определяем время, которое необходимо на один оборот с такой скоростью

переводим в минуты и часы и получаем, что это 1 час, 23 минуты и 37.9 секунды

Глава 5. Комплексные числа.

Решение многих задач физики и техники приводит к квадратным уравнениям с отрицательным дискриминантом. Эти уравнения не имеют решения в области действительных чисел. Но решение многих таких задач имеет вполне определенный физический смысл. Значение величин, получающихся в результате решения указанных уравнений, назвали комплексными числами.

Комплексные числа широко использовал отец русской авиации Н. Е. Жуковский (1847 – 1921) при разработке теории крыла, автором которой он является.

Комплексные числа и функции от комплексного переменного находят применение во многих вопросах науки и техники.

Но это совсем отдельный вопрос, он меня заинтересовал и может быть в 10 классе я познакомлюсь с этим числами и узнаю как решать квадратные уравнения с отрицательным дискриминантом.

Приобретать знания – храбрость,

Приумножать их – мудрость.

А умело применять — великое искусство!

В данной работе рассмотрена математическая модель — квадратное уравнение – которая позволят передать особенности изучаемого явления, реальной ситуации и решить её.

Рассмотрены виды уравнений, приёмы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения.

Данные приёмы решения заслуживают внимания, поскольку они не отражены в школьных учебниках математики. Овладение данными приёмами поможет мне экономить время и эффективно решать уравнения. Потребность в быстром решении обусловлена применением тестовой системы итоговых экзаменов в 9 и 11 классах.

Эта тема важна тем, что в результате ее изучения мы овладеете новым математическим аппаратом решения уравнений, позволяющим решать многообразные задачи не только математические, с помощью квадратных уравнений решаются текстовые задачи различных видов, находятся корни квадратного трехчлена, нули квадратичной функции (9 кл.), нахождение критических точек функции при исследовании функций, решение показательных, тригонометрических, логарифмических уравнений, приводимых к квадратным, нахождении пределов интегрирования(11кл.) Квадратные уравнения используются в курсе физики при решении задач по теме: «Равноускоренное движение», Падение тел» и других.

Научившийся решать квадратные уравнения со школьной скамьи (8 класс), знания могут пригодиться нам на протяжении всей жизни.

Я узнала , что квадратные уравнения с отрицательным дискриминантом решаются, но на не знакомом мне множестве чисел: на множестве комплексных чисел. Надеюсь что в старших классах узнаю об этом множестве чисел.

Задачи и цель, которые ставила в работе – знакомство с возникновение квадратных уравнений, рассмотрением различных способов решения квадратных уравнений, изучение приёмов устного решения квадратного уравнения, расширение знаний о применении квадратных уравнений в школьном образовании- достигнуты.

Работать было интересно, потому что я владела хорошими знаниями и навыками решения квадратных уравнений, узнала, что мои знания будут в дальнейшем востребованы на уроках математики и физики.

А Людмила Ивановна ещё считает, что отдельные главы моей работы могут быть использованы учителями математики при проведении элективного курса, дополнительной информацией при подготовке к уроку.

1. Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров, Н. Е. Федорова, М. И. Шабунин. Учебник 8 класса по алгебре.- М.: Просвещение, 2004.
2. И. С. Петраков. Математические кружки в 8-10 классах.- М.: Просвещение, 1987.
3. А. П. Савин. Энциклопедический словарь юного математика.- М.: Педагогика, 1989.
4. Г.И. Глейзер «История математики в школе»,- М.: Просвещение,1982.

элементов содержания по МАТЕМАТИКЕ для составления

контрольных измерительных материалов для проведения

в 2012 году единого государственного экзамена

• Квадратные уравнения
• Квадратные неравенства
• Квадратичная функция, ее график

Задачи, решаемые с помощью квадратных уравнений на ЕГЭ

Из пункта А в пункт В, расстояние между которыми 40 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 45 км больше, чем велосипедист.

Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 2 часа позже автомобилиста.

Ответ дайте в км/ч.

Из пункта А в пункт В, расстояние между которыми 60 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 45 км больше, чем велосипедист

Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 3 часа позже автомобилиста. Ответ дайте в км/ч.

Из пункта А в пункт В, расстояние между которыми 30 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 25 км больше, чем велосипедист.

Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 50 минут

позже автомобилиста. Ответ дайте в км/ч.

Прямая параллельна касательной к графику функции . Найдите абсциссу точки касания

Найдите наибольшее значение функции y = log 1/2 ( x 2 + 4 x + 8)

Найдите наибольшее значение функции на отрезке

y = ( x + 1)2( x − 3) − 2[−2; 0]

7 2х = 6·7 х + 5 = 0

• Решите уравнение .
• Найдите наименьший корень уравнения .
• Решите уравнение:
• Решите уравнение .
• Найдите сумму корней уравнения на промежутке [- π ;2 π ].

• Решите уравнение 6cos2 x − 7cos x − 5 = 0 .Укажите корни принадлежащие отрезку [− π ; 2 π ]
• Вычислите площадь фигуры, ограниченной линиями:

• Вычислите площадь фигуры, ограниченной линиями :

• Найдите тангенс угла наклона касательной к графику функции в точке с абсциссой .

• Укажите промежуток, на котором функция только возрастает .
• Найдите точку минимума функции .

Найдите наибольшее значение функции на отрезке .

Задачи с физическим содержанием, решаемые с помощью квадратных уравнений на ЕГЭ

Камень брошен вертикально вверх. Пока камень не упал, высота, на которой он находится, описывается формулой h ( t ) = −5 t ² +18 t , где h – высота в метрах, t – время в секундах, прошедшее с момента броска.

Сколько секунд камень находился на высоте не менее 9 метров.

В боковой стенке высокого цилиндрического бака у самого дна закреплен кран.

После его открытия вода начинает вытекать из бака, при этом высота столба воды в нем, выраженная в метрах, меняется по закону H ( t )= H 0 — √2 gH 0 kt + g,/2к²t² где — время в секундах, прошедшее с момента открытия крана, начальная высота столба H 0 = 5 м, k = 1/700

отношение площадей поперечных сечений крана и бака, ускорение свободного падения (считайте g = 10 м / с²) .Через сколько секунд после открытия крана в баке

останется четверть первоначального объема воды?

В боковой стенке высокого цилиндрического бака у самого дна закреплен кран.

После его открытия вода начинает вытекать из бака, при этом высота столба воды в нем, выраженная в метрах, меняется по закону H ( t )= H 0 — √2 gH 0 kt + g,/2к²t² где — время в секундах, прошедшее с момента открытия крана, начальная высота столба H 0 = 5 м, k = 1/900

отношение площадей поперечных сечений крана и бака, ускорение свободного падения (считайте g = 10 м / с²) .Через сколько секунд после открытия крана в баке

останется четверть первоначального объема воды?

Расстояние от наблюдателя, находящегося на небольшой высоте h километров над землей, до наблюдаемой им линии горизонта вычисляется по формуле L=√2RH , где R (км) — радиус Земли R = 6400 .C какой высоты горизонт виден на расстоянии 32 километра? Ответ выразите в километрах .

Высоту над землёй подброшенного вверх мяча можно вычислить по формуле h(t) = 1 + 11t – 5t² (h— высота в метрах, t — время в секундах, прошедшее с момента броска). Сколько секунд мяч будет находиться на высоте более 3 метров?

Зависимость объёма спроса q (единиц в месяц) на продукцию предприятия-монополиста

от цены p . (тыс. руб.) задается формулой q = 55 − 5 p r.

Выручка предприятия за месяц r (в тыс. руб.) вычисляется

по формуле r ( p ) = q p . ⋅

Определите наибольшую цену р, при которой месячная выручка r ( p ) составит 140 тыс. руб

Применение квадратных уравнений в жизни

Презентация к открытому уроку по алгебре в 8 классе по теме » Квадратные уравнения»

Просмотр содержимого документа
«Применение квадратных уравнений в жизни»

«Квадратные уравнения в жизни»

• Квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. Умение решать уравнения не только имеет теоретическое значение для познания естественных законов, но и служит практическим целям.

• Важность умения решать квадратные уравнения в очередной раз доказывает то, что такие уравнения умели решать еще в древности. Но как это делалось, если в то время не существовала символическая алгебра?

История возникновения и развития квадратных уравнений

• Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.

• Квадратные уравнения решали еще в Индии. Древнеиндийский математик Баудхаяма. впервые использовал квадратные уравнения в форме ax2= c и ax2+ bx = c и привел методы их решения.

• Формулы решения квадратных уравнений в Европе были впервые изложены в 1202 г. в «Книге абака» итальянским математиком Леонардом Фибоначчи.

• Далее квадратные уравнения продолжают изучать и другие выдающиеся математики

• Решение квадратных уравнений находило применение в древности.
• Так как квадратные уравнения с тех времен активно развивались, можно сделать вывод, что их применение значительно увеличилось. Как же теперь применяются квадратные уравнения?

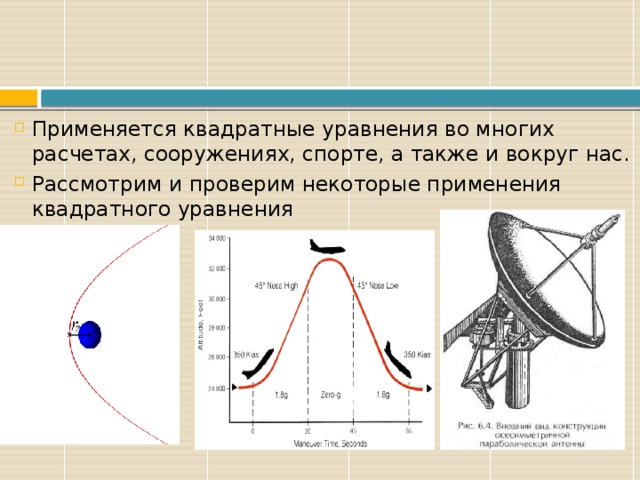
• Применяется квадратные уравнения во многих расчетах, сооружениях, спорте, а также и вокруг нас.
• Рассмотрим и проверим некоторые применения квадратного уравнения

• Сейчас ученые выяснили, что траекторию движения планет можно найти с помощью квадратного уравнения.

Взлет главная составляющая полета. Здесь берется расчет для маленького сопротивления и ускоренного взлета.

• Фонтан смотрится лучше, если капли воды достигают высоты, большей, чем высота статуи.

В данном виде спорта, крайне важны арифметические расчеты.

При разбеге прыгуна в высоту для максимально четкого попадания на планку отталкивания и высокого полета, используют расчеты связанные с парабалой.

Также подобные расчеты нужны в метании. Дальность полета объекта зависит от квадратного уравнения.

• Квадратные уравнения получили большое значение и значительное применение в жизни.

• Квадратное уравнение имеет большое применение в жизни. Еще в древности человек использовал квадратное уравнение. А с тех пор применение квадратного уравнения только росло.

• Проходя эту тему на уроке, мы мало задумываемся о практическом применении квадратных уравнений. Поэтому мы считаем, что квадратные уравнения нигде не используются, но как выяснилось это не так.

Исследовательская работа «Квадратные уравнения»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Муниципальное бюджетное общеобразовательное учреждение

«Сергачская средняя общеобразовательная школа №3»

Квадратные уравнения: от истоков к современности

Выполнила ученица 8 «а» класса

Никулина Анастасия, 14 лет

Руководитель: Маслова Елена Владимировна

3. Способы решения квадратных уравнений …………………………… ….10-15

С квадратными уравнениями мы знакомы из школьного курса алгебры. В учебнике алгебры 8 класса под редакцией С.А.Теляковского нам представляют квадратные уравнения, как уравнения второй степени. Предлагаются некоторые способы решения квадратных уравнений, а также решение задач с помощью квадратных уравнений. Но к сожалению, о применении уравнений на практике в учебнике ничего не сказано.

На уроке нам учитель сообщила, что есть и другие способы решения квадратных уравнений и можно для каждого вида уравнений выбрать эффективный способ. Я решила самостоятельно изучить способы решения квадратных уравнений, которых нет в учебнике, а также выяснить имеют ли применение в жизни квадратные уравнения.

Цель работы: Расширить свои знания о квадратных уравнениях

Познакомиться с историей появления и развития квадратных уравнений

Используя дополнительную литературу, изучить способы решения, которых нет в учебнике

Узнать применение квадратных уравнений в жизни

Объект исследования : квадратные уравнения

Предмет: исследования квадратных уравнений

Актуальность темы: Теория уравнений занимает ведущее место в алгебре и математике в целом. Сила теории уравнений в том, что не только имеет теоретическое значение для познания естественных законов, но и служит практическим целям. Большинство жизненных задач сводится к решению различных видов уравнений, и чаще это уравнения квадратного вида.

Гипотеза: Предполагаю, что квадратные уравнения можно решить многими способами, и они находят своё применение в жизни человека

Есть ли иные способы решения квадратных уравнений отличные от тех, что предложены в учебнике и зачем нам в жизни нужны квадратные уравнения

1 . Странички истории

Квадратные уравнения в Древнем Вавилоне

Много лет назад возникла необходимость решать уравнения второй степени. Потребность обусловлена нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:

Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.

При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные. Вот, к примеру, одна из его задач.

Задача «Найти два числа, зная, что их сумма равна 20, а произведение – 96».

Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так, как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т. е. 10+х. Другое же меньше, т. е.10- х . Разность между ними2х. Отсюда уравнение:

или же 100 – х 2 =96, х 2 =4

Отсюда х = 2 . Одно из искомых чисел равно 12, другое 8. Решение х = -2 для Диофанта не существует, так как греческая математика знала только положительные числа. Если решить эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то можно прийти к решению уравнения:

y (20- y ) = 96 , y 2 – 20 y +96=0

Ясно, что, выбирая в качестве неизвестного полу разность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения.

Квадратные уравнения в Индии

Задачи на квадратные уравнения встречаются уже в астрономическом трактате «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:

ax 2 + bx = c , а > 0 (1)

В уравнении (1) коэффициенты, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.

В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму. Вот одна из задач знаменитого индийского математика XII в. Бхаскары. «Стая обезьян забавляется: восьмая часть всего числа их в квадрате резвится в лесу, остальные двенадцать кричат на вершине холмика. Скажите мне, сколько всех обезьян?»

Комментируя задачу, хочется сказать, что задаче соответствует уравнение (х/8) 2 + 12 = x . Бхаскара пишет под видом x 2 – 64х = — 768. Прибавляя к обеим частям квадрат 32, уравнение примет вид:

x 2 – 64 x + 32 2 = — 768 + 1024

После извлечения квадратного корня получаем: x – 32 =16.

«В данном случае, говорит Бхаскара, — отрицательные единицы первой части таковы, что единицы второй части меньше их, а потому последние можно считать и положительными, и отрицательными, и получаем двойное значение неизвестного: 48 и 16». Необходимо сделать вывод: решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений.

Квадратные уравнения в Европе XII-XVII в.

Формы решения квадратных уравнений по образцу Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202г. итальянским математиком Леонардом Фибоначчи. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел.

Эта книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из этой книги переходили почти во все европейские учебники XIV-XVII вв. Общее правило решения квадратных уравнений, приведенных к единому каноническому виду х 2 + bx = c при всевозможных комбинациях знаков и коэффициентов b, c, было сформулировано в Европе в 1544 г. М. Штифелем.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.

Истоки алгебраических методов решения практических задач связаны с наукой древнего мира. Как известно из истории математики, значительная часть задач математического характера, решаемых египетскими, шумерскими, вавилонскими писцами-вычислителями (XX—VI вв. до н. э.), имела расчетный характер. Однако уже тогда время от времени возникали задачи, в которых искомое значение величины задавалось некоторыми косвенными условиями, требующими, с нашей современной точки зрения, составления уравнения или системы уравнений. Первоначально для решения таких задач применялись арифметические методы. В дальнейшем начали формироваться начатки алгебраических представлений. Например, вавилонские вычислители умели решать задачи, сводящиеся с точки зрения современной классификации к уравнениям второй степени. Был создан метод решения текстовых задач, послуживший в дальнейшем основой для выделения алгебраического компонента и его независимого изучения.

Это изучение осуществлялось уже в другую эпоху сначала арабскими математиками (VI—Х вв. н. э.), выделившими характерные действия, посредством которых уравнения приводились к стандартному виду приведение подобных членов, перенос членов из одной части уравнения в другую с переменой знака. А затем европейскими математиками Возрождения, в итоге длительного поиска создавшими язык современной алгебры, использование букв, введение символов арифметических операций, скобок и т. д. На рубеже XVI—XVII вв. алгебра как специфическая часть математики, обладающая своим предметом, методом, областями приложения, была уже сформирована. Дальнейшее ее развитие, вплоть до нашего времени, состояло в совершенствовании методов, расширении области приложений, уточнении понятий и связей их с понятиями других разделов математики.

Аль – Хорезми — арабский учёный, который в 825 г. написал книгу «Книга о восстановлении и противопоставлении». Это был первый в мире учебник алгебры. Он также дал шесть видов квадратных уравнений и для каждого из шести уравнений в словесной форме сформулировал особое правило его решения.

В трактате Хорезми насчитывает 6 видов уравнений, выражая их следующим образом:

1. «Квадраты равны корням», т.е. ах 2 = вх.

2. «Квадраты равны числу», т.е. ах 2 = с.

3. «Корни равны числу», т.е. ах = с.

4. «Квадраты и числа равны корням», т.е. ах 2 + с = вх.

5. «Квадраты и корни равны числу», т.е. ах 2 + вх = с.

6. «Корни и числа равны квадратам», т.е. вх +с = ах 2 .

Разберём задачу аль – Хорезми, которая сводится к решению квадратного уравнения. «Квадрат и число равны корням.» Например, один квадрат и число 21 равны 10 корням того же квадрата, т.е. спрашивается, из чего образуется квадрат, который после прибавления к нему 21 делается равным 10 корням того же квадрата?» х 2 + 21 = 10х

Франсуа Виет — французский математик, сформулировал и доказал теорему о сумме и произведении корней приведённого квадратного уравнения.

Искусство, которое я излагаю, ново или по крайней мере было настолько испорчено временем искажено влиянием варваров, что я счел нужным придать ему совершенно новый вид . Франсуа Виет

Виет Франсуа (1540-13.12. 1603) родился в городе Фонтене ле-Конт провинции Пуату, недалеко от знаменитой крепости Ла-Ро-шель. Он был широко образованным человеком. Знал астрономию и математику и все свободное время отдавал этим наукам.Главной страстью Виета была математика. Он глубоко изучил сочинения классиков Архимеда и Диофанта, ближайших предшественников Кардано, Бомбелли, Стевина и других. Виета они не только восхищали, в них он видел большой изъян, заключающийся в трудности понимания из-за словесной символики: Почти все действия и знаки записывались словами, не было намека на те удобные, почти автоматические правила, которыми мы сейчас пользуемся. Нельзя было записывать и, следовательно, начать в общем виде алгебраические сравнения или какие-нибудь другие алгебраические выражения. Каждый вид уравнения с числовыми коэффициентами решался по особому правилу. Поэтому необходимо было доказать, что существуют такие общие действия над всеми числами, которые от этих самих чисел не зависят. Виет и его последователи установи, что не имеет значения, будет ли рассматриваемое число количеством предметов или длиной отрезка. Главное, что с этими числами можно производить алгебраические действия и в результате снова получать числа того же рода. Значит, их можно обозначать какими-либо отвлеченными знаками. Виет это и сделал. Он не только ввел свое буквенное исчисление, но сделал принципиально новое открытий, поставив перед собой цель изучать не числа, а действия над ними. Такой способ записи позволил Виету сделать важные открытия при изучении общих свойств алгебраических уравнений. Не случайно за это Виета называют «отцом» алгебры, основоположником буквенной символики.

2. Способы решения квадратных уравнений

1. СПОСОБ : Разложение левой части уравнения на множители

2. СПОСОБ : Метод выделения полного квадрата

3. СПОСОБ : Решение квадратных уравнений по формуле

4. СПОСОБ : Графическое решение квадратного уравнения

5. СПОСОБ : Решение уравнений с использованием теоремы Виета

Все вышеперечисленные способы подробно разобраны в учебнике, поэтому на них я не буду останавливаться. Разберём ещё несколько способов.

6. СПОСОБ : Решение уравнений способом «переброски»

Рассмотрим квадратное уравнение ах 2 + bх + с = 0, где а ≠ 0.

Умножая обе его части на а, получаем уравнение а 2 х 2 + аbх + ас = 0.

Пусть ах = у , откуда х = у/а ; тогда приходим к уравнению у 2 + by + ас = 0, равносильно данному. Его корни у ₁ и у ₂ найдем с помощью теоремы Виета.

При этом способе коэффициент a умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски» . Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Решим уравнение 2х 2 — 11х + 15 = 0.

Решение. « Перебросим» коэффициент 2 к свободному члену и сделав замену получим уравнение у 2 — 11у + 30 = 0.

Согласно обратной теореме Виета

7. СПОСОБ: Свойства коэффициентов квадратного уравнения

Пусть дано квадратное уравнение ах 2 + bх + с = 0, а ≠ 0

1. Если a+ b + с = 0 ( т.е. сумма коэффициентов уравнения равна нулю), то х ₁ = 1, х ₂ = c/а

2. Если а — b + с = 0, или b = а + с, то х1 = — 1, х2 = — c/а

Решим уравнение 345х 2 — 137х — 208 = 0.

Решение : так как а + b + с = 0 (345 — 137 — 208 = 0), то х ₁ = 1, х ₂ = — 208/345

Решим уравнение 132х2 + 247х + 115 = 0

Решение. Т.к. a-b+с = 0 (132 — 247 +115=0), то

8. СПОСОБ: Решение квадратных уравнений с помощью циркуля и линейки

Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то потребуется много времени, и при этом степень точности получаемых результатов невелика. Можно использовать следующий способ нахождения корней квадратного уравнения ах2 + bх + с = 0 с помощью циркуля и линейки. Нужно найти координаты центра S окружности по формуле x ₀ = — b /2 a y ₀ = ( a + c )/2 a и провести окружность радиуса SA , где А(0,1)

При этом возможны три случая

1) Радиус окружности больше ординаты центра, окружность пересекает ось Ох в двух точках

х1 и х2 — корни квадратного уравнения ах2 + bх + с = 0.

2) Радиус окружности равен ординате центра, окружность касается оси Ох в точке

х ₁ — корень квадратного уравнения

3) Радиус окружности меньше ординаты центра, окружность не имеет общих точек с осью абсцисс, в этом случае уравнение не имеет решения.

Решим уравнение х 2 — 2х — 3 = 0.

Определим координаты точки центра окружности по формулам: х ₀ = 2/2=1, у ₀ = -2/2=-1

Проведем окружность радиуса S A, где А (0;1)

9. СПОСОБ : Геометрический способ решения квадратных уравнений

В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведем ставший знаменитым пример из «Алгебры» ал-Хорезми.

Решим уравнение х 2 + 10х = 39.

В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39».

Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата, сторона каждого их них 2,5, а площадь 6,25.

Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х 2 , четырех прямоугольников (4• 2,5х = 10х ) и четырех пристроенных квадратов (6,25• 4 = 25), т.е. S = х 2 + 10х + 25. Заменяя

х 2 + 10х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим

Решим геометрически уравнение у 2 — 6у — 16 = 0.

Преобразуя уравнение, получаем

Находим «изображения» выражения у 2 — 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3. Значит, если к выражению у 2 — 6у прибавить 9, то получим площадь квадрата со стороной у — 3. Заменяя выражение у 2 — 6у равным ему числом 16,

получаем: (у — 3) 2 = 16 + 9, т.е. у — 3 = ± √25, или у — 3 = ± 5, где у ₁ = 8 и у ₂ = — 2.

10. СПОСОБ: Решение уравнений с использованием теоремы Безу

Теорема Безу и её следствие рассматриваются в старших классах. Смысл состоит в том, что нужно подставить в уравнение вместо неизвестной все целые делители свободного члена уравнения, и поделить столбиком наш трехчлен на (х- а), где а – найденный корень. Затем разложить на множители и найти остальные корни. Приведу пример:

Разделим р (х) на (х-1)

3. Жизнь по «параболе»

Школьном курсе алгебры мы знакомимся с квадратными уравнениями и уравнениями, сводящимися к квадратным. Однако они применяются не только для решения более сложных уравнений. Мы встретим квадратные уравнения в экономических дисциплинах, в различных программах для обработки звука и видео, а также в векторной графике.

Многие обучающиеся даже не догадываются, что график квадратичной функции, парабола, встречается в разных областях нашей жизни. Приведу несколько примеров.

При разбеге прыгуна для максимально четкого попадания на планку отталкивания и высокого полета используют расчеты, связанные с параболой. Подобные расчеты нужны и при метании снаряда. Дальность полета объекта зависит от квадратного уравнения. Даже беговая дорожка стадиона, параболической формы, для плавного прохождения дистанции.

Наука и техника

Тесно связаны квадратные уравнения с астрономией. Ведь с их помощью можно найти траекторию движения планет. Человек давно начал освоение неба и одно из главных его изобретений — самолет. Взлет самолета главная составляющая полета. Здесь берется расчет для маленького сопротивления и ускорения взлета. Не обошлась без квадратных уравнений и военная техника. Русская артиллерия установила рекорд дальности стрельбы

Мы с удовольствием наблюдаем красивейшее оптическое явление – радуга. Еще ученые древности задавались вопросом формы радуги. Она полукруглая. Форма радуги определяется формой капель воды, в которых преломляется солнечный свет. А форма капли- круглая.

Даже струя воды, выбрасываемая из фонтана принимает форму параболы.

Дельфины – прекрасные создания. Они сопровождают суда и начинают выпрыгивать из воды, демонстрируя при этом движение по параболе.

Человечество прошло длинный путь от незнания к знанию, непрерывно заменяя на этом пути неполное и несовершенное знание все более полным и совершенным.

В ходе выполнения своей исследовательской работы я считаю, что с поставленной целью и задачами я справилась, мне удалось узнать о квадратных уравнениях гораздо больше, чем в школьном курсе алгебры. Мне было интересно узнать о различных способах решения квадратных уравнений, а также узнать где же они применяются. Способов решения квадратных уравнений очень много. Я изучила 10 способов решения квадратных уравнений. Надо отметить, что не все они удобны для решения, но каждый из них уникален. Некоторые способы решения помогают сэкономить время, что немаловажно при решении заданий на ГИА.

Подводя итоги, можно сделать вывод, что гипотеза моя подтвердилась. Квадратные уравнения играют огромную роль в математике. Эти знания могут пригодиться нам на протяжении всей жизни, и я думаю, что мою презентацию можно использовать в учебном процессе, чтобы заинтересовать увлекающихся математикой школьников и просто тех детей, которые не видят смысла в квадратных уравнениях

1.Мордкович А.Г. М 79 Алгебра. 8 класс: В двух частях. Ч.1: Учебник для общеобразовательных учреждений. — 4-е издание — М.: Мнемозина, 2002. — 223 с.:

2. Гусев В.А., Мордкович А.Г. Математика: Справочные материалы: Книга для учащихся. — М.: Просвещение, 1988

3.Глейзер Г.И. История математики в школе. — М.: просвещение, 1982

4.Брадис В.М. Четырехзначные математические таблицы для средней школы. — м., просвещение, 1990

5.Окунев А.К. Квадратичные функции, уравнения и неравенства. Пособие для учителя. — М.: Просвещение, 1972

6.Пресман А.А. Решение квадратного уравнения с помощью циркуля и линейки.М., Квант, №4/72. С.34.

7.Дидактические материалы по алгебре. М., Математика (приложение к газете «Первое сентября»), №№ 21/96, 10/97.

8.Баранова Е.А. Как увлечь школьников исследовательской деятельностью. Математика в школе / Е.А. Баранова, М.И.Зайкин// 2004. №2 – 80с.

9.Глейзер Г.И. История математики в школе. 7-8 классы. – М.: Просвещение, 1982.

10.Дробышев Ю.А. Изучение квадратных уравнений на основе историко – генетического метода /Ю.А. Дробышев // /. Математика в школе № 6 –2011.

11.С.А. Литвинова, и др. За страницами учебника математики 8-11 классы. – 2-е изд., дополненное – М.: Глобус, Волгоград: Панорама,2008.– c.76-82.

12.Макарычев Ю. Н. Алгебра: учебник для 8 класса общеобразовательных учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под редакцией С. А. Теляковского. – 11-е издание – М.: Просвещение, 2003. – 238 с.