Для чего нужны квадратные уравнения

Применение квадратных уравнений в жизни

Презентация к открытому уроку по алгебре в 8 классе по теме » Квадратные уравнения»

Просмотр содержимого документа
«Применение квадратных уравнений в жизни»

«Квадратные уравнения в жизни»

• Квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. Умение решать уравнения не только имеет теоретическое значение для познания естественных законов, но и служит практическим целям.

• Важность умения решать квадратные уравнения в очередной раз доказывает то, что такие уравнения умели решать еще в древности. Но как это делалось, если в то время не существовала символическая алгебра?

История возникновения и развития квадратных уравнений

• Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.

• Квадратные уравнения решали еще в Индии. Древнеиндийский математик Баудхаяма. впервые использовал квадратные уравнения в форме ax2= c и ax2+ bx = c и привел методы их решения.

• Формулы решения квадратных уравнений в Европе были впервые изложены в 1202 г. в «Книге абака» итальянским математиком Леонардом Фибоначчи.

• Далее квадратные уравнения продолжают изучать и другие выдающиеся математики

• Решение квадратных уравнений находило применение в древности.
• Так как квадратные уравнения с тех времен активно развивались, можно сделать вывод, что их применение значительно увеличилось. Как же теперь применяются квадратные уравнения?

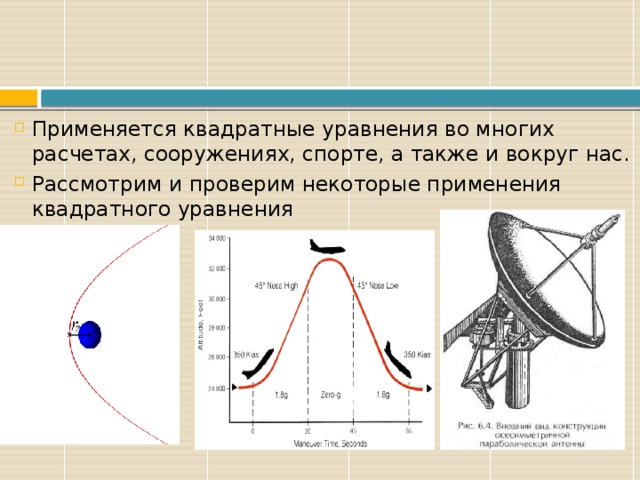
• Применяется квадратные уравнения во многих расчетах, сооружениях, спорте, а также и вокруг нас.
• Рассмотрим и проверим некоторые применения квадратного уравнения

• Сейчас ученые выяснили, что траекторию движения планет можно найти с помощью квадратного уравнения.

Взлет главная составляющая полета. Здесь берется расчет для маленького сопротивления и ускоренного взлета.

• Фонтан смотрится лучше, если капли воды достигают высоты, большей, чем высота статуи.

В данном виде спорта, крайне важны арифметические расчеты.

При разбеге прыгуна в высоту для максимально четкого попадания на планку отталкивания и высокого полета, используют расчеты связанные с парабалой.

Также подобные расчеты нужны в метании. Дальность полета объекта зависит от квадратного уравнения.

• Квадратные уравнения получили большое значение и значительное применение в жизни.

• Квадратное уравнение имеет большое применение в жизни. Еще в древности человек использовал квадратное уравнение. А с тех пор применение квадратного уравнения только росло.

• Проходя эту тему на уроке, мы мало задумываемся о практическом применении квадратных уравнений. Поэтому мы считаем, что квадратные уравнения нигде не используются, но как выяснилось это не так.

Роль и место квадратных уравнений в образовательном процессе школьников

2014г. ученица 9 Б класса

Тема: «Роль и место квадратных уравнений в образовательном процессе школьников»

(проблемно –исследовательская работа)

Скачать:

Предварительный просмотр:

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №9 г. Холмска

муниципального образования «Холмский городской округ»

Тема: «Роль и место квадратных уравнений в образовательном процессе школьников»

(проблемно –исследовательская работа)

ученица 9-б класса

Руководитель: учитель математики

Глава 1.История квадратных уравнений. 5

Глава 2.Математичская модель — квадратные уравнения и его корни. 8

1. Неполное квадратное уравнение; 8
2. Метод выделения полного квадрата; 8
3. Решение квадратных уравнений по формуле; 9
4. Теорема Виета; 10
5. Биквадратные уравнения. 11

Глава 3.Приёмы устного решения квадратного уравнения. 12

3.1 Свойства коэффициентов квадратного уравнения; 12

3.2 Приём «Переброски». 13

Глава 4.Квадратные уравнения в предметах естественно-математического цикла. 14

Глава 5.Комплексные числа. 15

Список литературы. 17

Ресурсы Интернета. 17

« Мне приходилось делить свое время между политикой и уравнениями . однако уравнения, по –моему, гораздо важнее, потому что политика существует только для данного момента, а уравнения будут существовать вечно.»

Школьник начальных классов, только приступивший к изучению арифметики, скажет, что математика изучает правила счёта предметов, школьники постарше добавит к сказанному, что в понятие математики входят алгебра и геометрия, а выпускники средней школы включат в определение математики ещё изучение тригонометрии, вычисление производных и интеграла.

Любой восьмиклассник нашей школы особенно выделит, что математика изучает квадратные уравнения.

После изучения темы: Квадратные уравнения» наша учительница по математике Л.И. Рязанцева проводит урок- отчёт. И вот какое стихотворение написал один из её учеников:

Квадратным уравнениям посвящается

Ах, уравнения, квадратные,

вы такие разные – распрекрасные

полные, неполные, приведенные.

Коэффициент у вас буквы латинские –

а, в и с величаемы.

И пути решения у всех разные –

разложи, перенеси, дискриминант найди.

А дискриминант в² — 4ас формула особая,

к полному и приведённом уравнению

Ах, уравнения, квадратные,

вы такие разные и корней у вас

количество разное – от двух корней

до пустого множества.

Квадратные уравнения – это математическая модель, которая позволят передать особенности изучаемого явления, ситуации.

Математическая модель — приближённое описание какого-либо класса явлений внешнего мира, выраженное с помощью математической символики. Математ и ческая мод е ль — мощный метод познания внешнего мира, а также прогнозирования и управления.

Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении многих текстовых задач, при решении неравенств второй степени и дробно- рациональных, при решении биквадратных, тригонометрических, показательных, иррациональных уравнений. Решение многих задач физики сводится к решению алгебраических и квадратных уравнений.

В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения.

Однако имеются и другие приёмы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения.

Данные приёмы решения заслуживают внимания, поскольку они не отражены в школьных учебниках математики.

Овладение данными приёмами поможет мне экономить время и эффективно решать уравнения. Потребность в быстром решении обусловлена применением тестовой системы итоговых экзаменов в 9 и 11 классах.

Я провела опрос старшеклассников:

1. Умеете вы решать квадратное уравнение?

8-б да! недавно изучали, 100%

1. Где применяются решения квадратных уравнений?

8-б – при решении задач из учебника.

9-б – при решении текстовых задач; при нахождении нулей квадратичной функции; при разложении квадратного трёхчлена на множители;

при решении квадратных неравенств;

при решении биквадратных уравнений;

при решении алгебраических уравнений, сводящихся к квадратным.

11-а – очень часто на уроках математики — при решении тригонометрических, показательных, логарифмических, иррациональных уравнений и неравенств;

при исследовании функций с помощью производной;

при нахождении пределов интегрирования;

на уроках физики.

1. Используешь ли ты при решении уравнений свойства коэффициентов?

Знакомясь с содержанием и структурой диагностических тестов ГИА, я подсчитала, что в среднем 23% всех заданий требуют умения решать квадратные уравнения.

Поэтому меня и заинтересовала эта тема.

1. Познакомиться с историей возникновения квадратных уравнений

2. Рассмотреть способы решения квадратных уравнений: метод выделения полного квадрата, решение квадратных уравнений по формуле, теорема Виета.

3.Изучить приёмы устного решения квадратного уравнения.

4.Узнать на уроках каких предметов задачи решаются с помощью квадратных уравнений.

5. Изучить структуру и содержание КИМ ГИА.

Гипотеза: знания различных способов решения квадратных уравнений и приёмов устного решения квадратных уравнений способствует быстрому и правильному решению задач и экономит время.

Задачи: Квадратные уравнения – это математическая модель реальности и её применение в школьном образовании.

Глава 1. История квадратных уравнений.

Квадратные уравнения в Древнем Вавилоне.

Необходимость решать уравнения не только первой, но и второй степени ещё в древности была вызвана потребность решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет назад до н. э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:

Правило решения этих уравнений, изложено в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты переводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.

Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

Как составлял и решал Диофант квадратные уравнения.

В “Арифметике” Диофант нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.

При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.

Вот, к примеру, одна из его задач.

Задача 11. “Найти два числа, зная, что их сумма равна 20, а произведение – 96” .

Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т. е. 10 – x. Разность между ними 2x. Отсюда уравнение

(10 + x) (10 – x) = 96,

Отсюда x = 2. Одно из искомых чисел равно 12, другое 8. Решение x = -2 для Диофанта не существует, так как греческая математика знала только положительные числа.

Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения.

y² – 20y + 96 = 0 (2)

Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удаётся свести задачу к решению не полного квадратного уравнения(1).

Квадратные уравнения в Индии

Задачи на квадратные уравнения встречаются уже в 499г. В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее:

« Как солнце блеском своим затмевает звёзды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи».

Одна из задач знаменитого индийского математика XIIв. Бхаскары:

Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений. Часть страницы из алгебры Бхаскары (вычисление корней).

Квадратные уравнения у ал-Хорезми

В алгебраическом трактате ал-Хорезми даётся классификация линейных уравнений и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:

1) “Квадраты равны корнями”, т. е. ax² = bx.

2) “Квадраты равны числу”, т. е. ax²= c.

3) “Корни равны числу”, т. е. ax = c

4) “Квадраты и числа равны корням”, т. е. ax² + c = bx/

5) “Квадраты и корни равны числу”, т. е. ax² + bx = c.

6) “Корни и числа равны квадратам”, т. е. bx + c + ax²

Для ал-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приёмами ал-джабар и ал-мукабала. Его решения, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида ал-Хорезми, как и все математики до 17 века, не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений ал-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.

Квадратные уравнения в Европе XIII — XVIIв.в.

Формулы решения квадратных уравнений по образцу ал-Хорезми в Европе были впервые изложены в книге “Книге абака”, написанной в 1202 г. Итальянским математиком Леонардо Фибоначчи. Этот объёмистый труд, в котором отражено влияние математики как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические примеры задач и первый в Европе подошёл к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других стран Европы. Многие задачи из “Книги абака” переходили почти во все европейские учебники 16 – 17 веков и частично 18 века. Общее правило решения квадратных уравнений, приведённых к единому каноническому виду: x² + bx = c,

при всевозможных комбинациях знаков коэффициентов b, c было сформулировано в Европе лишь в 1544 г. М.Штифелем.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в 16 веке учитывают, помимо положительных, и отрицательные корни. Лишь в 17 веке благодаря трудам Жирара, Декарта, Ньютона и других учёных способов решения квадратных уравнений принимает современный вид.

Квадратные уравнения – это математическая модель, которая позволят передать особенности изучаемого явления, реальной ситуации.

2.1 Квадратные уравнения и его корни

Квадратным уравнением называется уравнение ах² + bх + с = 0, где а≠0, а, b,с – заданные числа числа, х – неизвестное.

Коэффициенты а, b,с квадратного уравнения называют так: а- первым или старшим коэффициентом, b-вторым коэффициентом, с-свободным членом.

Неполное квадратное уравнение

Квадратное уравнение ах² + bх + с = 0 называют неполным , если хотя бы один из коэффициентов b или с равен нулю.

2) ах² + с = 0, ах² = -с

1. если с>0 , то нет действительных корней

2. если с , то х²= -с/а

2.2 Метод выделения полного квадрата

Пример1: решить квадратное уравнение

• Преобразуем это уравнение так:

Следовательно, х+1=2 или х+1= -2, откуда х1=1, х2= -3.

Решая уравнение, мы преобразовали его так, что в левой части получился квадрат двучлена, а правая часть не содержит неизвестное.

2.3 Решение квадратных уравнений по формуле.

Если D , то уравнение не имеет действительных корней

Пример1: х² — 4х +5 =0

D , то уравнение не имеет действительных корней

Пример2: 2х² + 3х + 1 = 0

«Виет – творец математической формулы.»

«Французский геометр Виет был выше всех своих современников. Он прославился обобщением алгебры и сделал несколько важных открытий в этой отрасли человеческих знаний.»

Решение уравнений с использованием теоремы Виета.

Как известно, приведенное квадратное уравнение имеет вид

х 2 + px + c = 0. (1)

Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид

x 1 x 2 = q,

Т.е., сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).

а) Если сводный член q приведенного уравнения (1) положителен ( q > 0 ), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p . Если р , то оба корня отрицательны, если р , то оба корня положительны.

x 2 – 3x + 2 = 0; x 1 = 2 и x 2 = 1, так как q = 2 > 0 и p = — 3

x 2 + 8x + 7 = 0; x 1 = — 7 и x 2 = — 1, так как q = 7 > 0 и p= 8 > 0.

б) Если свободный член q приведенного уравнения (1) отрицателен ( q ), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p , или отрицателен, если p > 0 .

x 2 + 4x – 5 = 0; x 1 = — 5 и x 2 = 1, так как q= — 5 и p = 4 > 0;

x 2 – 8x – 9 = 0; x 1 = 9 и x 2 = — 1, так как q = — 9 и p = — 8

Пример1: х² — 14х – 15 =0

Теорема Виета для полного квадратного уравнения:

По праву достойна в стихах быть воспета

О свойствах корней теорема Виета.

Что лучше, скажи, постоянства такого:

Умножишь ты корни – и дробь уж готова?

В числителе с, в знаменателе а.

А сумма корней тоже дроби равна.

Хоть с минусом дробь, что за беда.

В числителе в, b знаменателе а.

2.5 Биквадратные уравнения.

Биквадратным уравнением — называется уравнение вида ax 4 + bx 2 + c = 0 .

Биквадратное уравнение приводится к квадратному уравнению при помощи подстановки .

Новое квадратное уравнение относительно переменной :

Решая это уравнение, мы получаем корни квадратного уравнения и . Решая эти два уравнения ( и ) относительно переменной , мы получаем корни данного биквадратного уравнения.

Алгоритм решения биквадратных уравнений :

1. Ввести новую переменную
2. Подставить данную переменную в исходное уравнение
3. Решить квадратное уравнение относительно новой переменной
4. После нахождения корней ( ) подставить их в нашу переменную и найти исходные корни биквадратного уравнения

Решим биквадратное уравнение . Сначала приводим это уравнение к квадратному. Для этого введем вспомогательное неизвестное такое, что . Тогда . Теперь данное биквадратное уравнение приводится к виду:

Решая это квадратное уравнение, мы получим , . Так как , то данное биквадратное уравнение эквивалентно системе двух уравнений:

Решим каждое из этих уравнений и найдем объединение множеств их решений.

Глава 3. Приёмы устного решения квадратного уравнения.

1. Свойства коэффициентов квадратного уравнения:

Пусть дано квадратное уравнение ах 2 + bх + с = 0, где а ≠ 0.

1) Если, а + b + с = 0 (т.е. сумма коэффициентов равна нулю), то х 1 = 1,

Доказательство: Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение

x 2 + b/a • x + c/a = 0.

Согласно теореме Виета

По условию а – b + с = 0, откуда b = а + с. Таким образом,

x 1 + x 2 = — а + b/a= -1 – c/a,

x 1 x 2 = — 1• ( — c/a),

т.е. х 1 = -1 и х 2 = c/a, что и требовалось доказать.

1)Решим уравнение 345х 2 – 137х – 208 = 0.

Решение. Так как, а + b + с = 0 (345 – 137 – 208 = 0), то

х 1 = 1, х 2 = c/a = -208/345.

2)Решим уравнение 132х 2 – 247х + 115 = 0.

Решение. Так как, а + b + с = 0 (132 – 247 + 115 = 0), то

х 1 = 1, х 2 = c/a = 115/132.

3)Решим уравнение 5х 2 – 8х + 3 = 0.

Решение. Так как 5 – 8 + 3 = 0, то х 1 = 1; х 2 = 0,6.

Если в квадратном уравнении ах² + bх + с = 0 выполняется равенство а + с = в, то х1 = -1; х2 = — с/а.

1) 5х 2 – 8х + 3 = 0.

Так как 5 – 8 + 3 = 0, то х 1 = 1; х 2 = 0,6.

2) Решить уравнения с большими коэффициентами :

1) 319х² + 1988x + 1669 = 0.

х 1 = — 1; х 2 = -1669/319.

2) 839х² – 448x – 391 = 0.

х 1 = 1; х 2 = -391/839.

3) 939х² + 978x + 39 = 0.

х 1 = — 1; х 2 = -39/939.

3.2 Приём «Переброски»

Рассмотрим квадратное уравнение

ах 2 + bх + с = 0, где а ≠ 0.

Умножая обе его части на а, получаем уравнение

а 2 х 2 + аbх + ас = 0.

Пусть ах = у , откуда х = у/а ; тогда приходим к уравнению

равносильно данному. Его корни у 1 и у 2 найдем с помощью теоремы Виета.

Окончательно получаем х 1 = у 1 /а и х 1 = у 2 /а . При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски» . Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

1) Решим уравнение 2х 2 – 11х + 15 = 0.

Решение . «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение

у 2 – 11у + 30 = 0.

Согласно теореме Виета:

у 1 = 5 х 1 = 5/2 x 1 = 2,5

у 2 = 6 x 2 = 6/2 x 2 = 3.

2) Решим уравнение 6х² — 7х – 3 = 0

Глава 4. Квадратные уравнения в предметах естественно-математического цикла .

Задача 1. Вертикально вверх с начальной скоростью 7 м/с брошен камень. Через некоторое время =0,41 с после этого брошен вертикально вверх другой камень с такой же скоростью. На какой высоте (от земли ) встретятся камни?

Решение: Необходимо составить уравнения движения для обоих тел. После чего объединить их и решить. Движение равноускоренное вдоль прямой, поэтому векторы не нужны и сразу пишем уравнения движения в скалярной форме. Ось координат направим вверх, тогда для скорости

V1 = V01 — g * t (поскольку начальная скорость направлена против силы тяжести.)

откуда для координаты

Х1 = Х01 + V01 * t — g * t * t / 2

для второго тела выпущенного в момент времени t1 = t + dt уравнение движения будет иметь вид

Х2 = Х02 + V02 * (t + dt) — g * (t + dt) * (t + dt) / 2

При встрече тел их координаты совпадут, что на языке математики запишется как

Х01 + V01 * t — g * t * t / 2 = Х02 + V02 * (t + dt) — g * (t + dt) * (t + dt) / 2

поскольку тела запускаются из одной и той же точки и с одной и той же скоростью, то

Х01 = Х02 и V01 = V02

и окончательно уравнение принимает вид

V0 * t — g * t * t / 2 = V0 * (t + dt) — g * (t + dt) * (t + dt) / 2

У полученного квадратного уравнения относительно t может быть два, одно или ни одного решения. Нас будут интересовать решения с t > 0. Решения с t

Задача 2. Груз свободно падает с высоты 500 метров. Какое расстояние преодолевает груз за последнюю секунду своего падения?

Решение: Потенциальная энергия переходит в кинетическую

v = корень квадратный(2*g*h) — это скорость в момент удара

Рассмотрим обратный процесс примем скорость v за начальную при движении вверх, тогда пройденный путь s=v*t-g*t^2/2.

Так как t=1, то s=v-g/2 = корень квадратный(2*g*h) -g/2 = 100-5=95 метров

Задача 3. Ускорение свободного падения на Земле равно 10 м/с. Какой продолжительности должны быть сутки, чтобы тела на экваторе были невесомы?

Решение: Центростремительное ускорение есть v^2/R и оно же должно равняться ускорению свободного падения g

отсюда следует, что линейная скорость точки на экваторе должна быть

далее определяем время, которое необходимо на один оборот с такой скоростью

переводим в минуты и часы и получаем, что это 1 час, 23 минуты и 37.9 секунды

Глава 5. Комплексные числа.

Решение многих задач физики и техники приводит к квадратным уравнениям с отрицательным дискриминантом. Эти уравнения не имеют решения в области действительных чисел. Но решение многих таких задач имеет вполне определенный физический смысл. Значение величин, получающихся в результате решения указанных уравнений, назвали комплексными числами.

Комплексные числа широко использовал отец русской авиации Н. Е. Жуковский (1847 – 1921) при разработке теории крыла, автором которой он является.

Комплексные числа и функции от комплексного переменного находят применение во многих вопросах науки и техники.

Но это совсем отдельный вопрос, он меня заинтересовал и может быть в 10 классе я познакомлюсь с этим числами и узнаю как решать квадратные уравнения с отрицательным дискриминантом.

Приобретать знания – храбрость,

Приумножать их – мудрость.

А умело применять — великое искусство!

В данной работе рассмотрена математическая модель — квадратное уравнение – которая позволят передать особенности изучаемого явления, реальной ситуации и решить её.

Рассмотрены виды уравнений, приёмы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения.

Данные приёмы решения заслуживают внимания, поскольку они не отражены в школьных учебниках математики. Овладение данными приёмами поможет мне экономить время и эффективно решать уравнения. Потребность в быстром решении обусловлена применением тестовой системы итоговых экзаменов в 9 и 11 классах.

Эта тема важна тем, что в результате ее изучения мы овладеете новым математическим аппаратом решения уравнений, позволяющим решать многообразные задачи не только математические, с помощью квадратных уравнений решаются текстовые задачи различных видов, находятся корни квадратного трехчлена, нули квадратичной функции (9 кл.), нахождение критических точек функции при исследовании функций, решение показательных, тригонометрических, логарифмических уравнений, приводимых к квадратным, нахождении пределов интегрирования(11кл.) Квадратные уравнения используются в курсе физики при решении задач по теме: «Равноускоренное движение», Падение тел» и других.

Научившийся решать квадратные уравнения со школьной скамьи (8 класс), знания могут пригодиться нам на протяжении всей жизни.

Я узнала , что квадратные уравнения с отрицательным дискриминантом решаются, но на не знакомом мне множестве чисел: на множестве комплексных чисел. Надеюсь что в старших классах узнаю об этом множестве чисел.

Задачи и цель, которые ставила в работе – знакомство с возникновение квадратных уравнений, рассмотрением различных способов решения квадратных уравнений, изучение приёмов устного решения квадратного уравнения, расширение знаний о применении квадратных уравнений в школьном образовании- достигнуты.

Работать было интересно, потому что я владела хорошими знаниями и навыками решения квадратных уравнений, узнала, что мои знания будут в дальнейшем востребованы на уроках математики и физики.

А Людмила Ивановна ещё считает, что отдельные главы моей работы могут быть использованы учителями математики при проведении элективного курса, дополнительной информацией при подготовке к уроку.

1. Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров, Н. Е. Федорова, М. И. Шабунин. Учебник 8 класса по алгебре.- М.: Просвещение, 2004.
2. И. С. Петраков. Математические кружки в 8-10 классах.- М.: Просвещение, 1987.
3. А. П. Савин. Энциклопедический словарь юного математика.- М.: Педагогика, 1989.
4. Г.И. Глейзер «История математики в школе»,- М.: Просвещение,1982.

элементов содержания по МАТЕМАТИКЕ для составления

контрольных измерительных материалов для проведения

в 2012 году единого государственного экзамена

• Квадратные уравнения
• Квадратные неравенства
• Квадратичная функция, ее график

Задачи, решаемые с помощью квадратных уравнений на ЕГЭ

Из пункта А в пункт В, расстояние между которыми 40 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 45 км больше, чем велосипедист.

Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 2 часа позже автомобилиста.

Ответ дайте в км/ч.

Из пункта А в пункт В, расстояние между которыми 60 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 45 км больше, чем велосипедист

Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 3 часа позже автомобилиста. Ответ дайте в км/ч.

Из пункта А в пункт В, расстояние между которыми 30 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 25 км больше, чем велосипедист.

Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 50 минут

позже автомобилиста. Ответ дайте в км/ч.

Прямая параллельна касательной к графику функции . Найдите абсциссу точки касания

Найдите наибольшее значение функции y = log 1/2 ( x 2 + 4 x + 8)

Найдите наибольшее значение функции на отрезке

y = ( x + 1)2( x − 3) − 2[−2; 0]

7 2х = 6·7 х + 5 = 0

• Решите уравнение .
• Найдите наименьший корень уравнения .
• Решите уравнение:
• Решите уравнение .
• Найдите сумму корней уравнения на промежутке [- π ;2 π ].

• Решите уравнение 6cos2 x − 7cos x − 5 = 0 .Укажите корни принадлежащие отрезку [− π ; 2 π ]
• Вычислите площадь фигуры, ограниченной линиями:

• Вычислите площадь фигуры, ограниченной линиями :

• Найдите тангенс угла наклона касательной к графику функции в точке с абсциссой .

• Укажите промежуток, на котором функция только возрастает .
• Найдите точку минимума функции .

Найдите наибольшее значение функции на отрезке .

Задачи с физическим содержанием, решаемые с помощью квадратных уравнений на ЕГЭ

Камень брошен вертикально вверх. Пока камень не упал, высота, на которой он находится, описывается формулой h ( t ) = −5 t ² +18 t , где h – высота в метрах, t – время в секундах, прошедшее с момента броска.

Сколько секунд камень находился на высоте не менее 9 метров.

В боковой стенке высокого цилиндрического бака у самого дна закреплен кран.

После его открытия вода начинает вытекать из бака, при этом высота столба воды в нем, выраженная в метрах, меняется по закону H ( t )= H 0 — √2 gH 0 kt + g,/2к²t² где — время в секундах, прошедшее с момента открытия крана, начальная высота столба H 0 = 5 м, k = 1/700

отношение площадей поперечных сечений крана и бака, ускорение свободного падения (считайте g = 10 м / с²) .Через сколько секунд после открытия крана в баке

останется четверть первоначального объема воды?

В боковой стенке высокого цилиндрического бака у самого дна закреплен кран.

После его открытия вода начинает вытекать из бака, при этом высота столба воды в нем, выраженная в метрах, меняется по закону H ( t )= H 0 — √2 gH 0 kt + g,/2к²t² где — время в секундах, прошедшее с момента открытия крана, начальная высота столба H 0 = 5 м, k = 1/900

отношение площадей поперечных сечений крана и бака, ускорение свободного падения (считайте g = 10 м / с²) .Через сколько секунд после открытия крана в баке

останется четверть первоначального объема воды?

Расстояние от наблюдателя, находящегося на небольшой высоте h километров над землей, до наблюдаемой им линии горизонта вычисляется по формуле L=√2RH , где R (км) — радиус Земли R = 6400 .C какой высоты горизонт виден на расстоянии 32 километра? Ответ выразите в километрах .

Высоту над землёй подброшенного вверх мяча можно вычислить по формуле h(t) = 1 + 11t – 5t² (h— высота в метрах, t — время в секундах, прошедшее с момента броска). Сколько секунд мяч будет находиться на высоте более 3 метров?

Зависимость объёма спроса q (единиц в месяц) на продукцию предприятия-монополиста

от цены p . (тыс. руб.) задается формулой q = 55 − 5 p r.

Выручка предприятия за месяц r (в тыс. руб.) вычисляется

по формуле r ( p ) = q p . ⋅

Определите наибольшую цену р, при которой месячная выручка r ( p ) составит 140 тыс. руб

Для чего нужны квадратные уравнения

История квадратных уравнений

Необходимость решать уравнения не только первой степени, но и второй ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков, с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне. Правила решения этих уравнений, изложенные в вавилонских текстах, совпадает по существу с современными, но в этих текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

Решением квадратных уравнений занимались и в Древней Греции такие ученые как Диофант, Евклид и Герон. Диофант Диофант Александрийский – древнегреческий математик, живший предположительно в III веке нашей эры. Основное произведение Диофанта – «Арифметика» в 13 книгах. Евклид. Евклид древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике Герон. Герон – греческий математик и инженер впервые в Греции в I век н.э. дает чисто алгебраический способ решения квадратного уравнения

Задачи на квадратные уравнения встречаются уже в астрономическом трактате «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме: ax2 + bх = с, а> 0. (1) В уравнении (1) коэффициенты, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим. В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.

Вот одна из задач знаменитого индийского математика XII в. Бхаскары.

«Обезьянок резвых стая

А двенадцать по лианам Всласть поевши, развлекалась

Стали прыгать, повисая

Их в квадрате часть восьмая

Сколько ж было обезьянок,

На поляне забавлялась

Ты скажи мне, в этой стае?»

Решение Бхаскары свидетельствует о том, что автор знал о двузначности корней квадратных уравнений. Соответствующее задаче уравнение Бхаскара пишет под видом x2 — 64x = — 768 и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 322, получая затем: x2 — б4х + 322 = -768 + 1024, (х — 32)2 = 256, х — 32= ±16, x1 = 16, x2 = 48.

Квадратные уравнения в Европе XVII века

Формулы решения квадратных уравнений по образцу Ал — Хорезми в Европе были впервые изложены в « Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи. Этот объемистый труд, в котором отражено влияние математики, как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из « Книги абака» переходили почти во все европейские учебники XVI — XVII вв. и частично XVIII. Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. Учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. Благодаря труда Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.

Определение квадратного уравнения

Уравнение вида ax 2 + bx + c = 0, где a, b, c — числа, , называется квадратным.

Коэффициенты квадратного уравнения

Числа а, b, с – коэффициенты квадратногоуравнения.а – первый коэффициент (перед х²), а ≠ 0;b — второй коэффициент (перед х);с – свободный член (без х).

Какие из данных уравнений не являются квадратными?

1. 4х² + 4х + 1 = 0;2. 5х – 7 = 0;3. — х² — 5х – 1 = 0;4. 2/х² + 3х + 4 = 0;5. ¼ х² — 6х + 1 = 0;6. 2х² = 0;

7. 4х² + 1 = 0;8. х² — 1/х = 0;9. 2х² – х = 0;10. х² -16 = 0;11. 7х² + 5х = 0;12. -8х²= 0;13. 5х³ +6х -8= 0.