Для данных повторных интегралов написать уравнения кривых

Будь умным!

Работа добавлена на сайт samzan.ru: 2015-07-05

Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой — мы готовы помочь.

;font-family:’Comic Sans MS'» xml:lang=»ru-RU» lang=»ru-RU»>Математический анализ 1 курс 2 семестр

» xml:lang=»ru-RU» lang=»ru-RU»>ЗАНЯТИЕ № » xml:lang=»en-US» lang=»en-US»>10

» xml:lang=»ru-RU» lang=»ru-RU»>Двойные интегралы.

» xml:lang=»ru-RU» lang=»ru-RU»>Задачи для решения в аудитории.

» xml:lang=»ru-RU» lang=»ru-RU»>1. Записать двойной интеграл в виде повторных, взятых в разных порядках. Перейти к полярным координатам и расставить пределы интегрирования по новым переменным, если область задана графически:

» xml:lang=»ru-RU» lang=»ru-RU»>2. Вычислить повторные интегралы, изобразить области интегрирования для (а) и (б):

» xml:lang=»ru-RU» lang=»ru-RU»> (а) (б) (в)

» xml:lang=»ru-RU» lang=»ru-RU»>3. Для указанных областей » xml:lang=»en-US» lang=»en-US»>G » xml:lang=»ru-RU» lang=»ru-RU»> записать двойной интеграл в виде повторных, взятых в разных порядках, сделать рисунок:

» xml:lang=»ru-RU» lang=»ru-RU»> (а) (б)

3.Изменить порядок интегрирования в повторных интегралах, сделать рисунок:

4.Вычислить (сделать чертеж):

, где область G ограничена кривыми

5. Найти среднее значение функции в треугольнике с вершинами

Обязательное домашнее задание:

1. Вычислить повторные интегралы:

2. Для данных повторных интегралов написать уравнения кривых, ограничивающих области интегрирования, и построить эти области

3. Изменить порядок интегрирования: 3.1.

где область интегрирования ограничена кривыми

где область интегрирования ограничена кривыми

Узнать стоимость написания работы —>

Материалы собраны группой SamZan и находятся в свободном доступе

Вычисление двойных интегралов: теория и примеры

Что значит вычислить двойной интеграл?

Двойные интегралы – это обобщение понятия определённого интеграла для функции двух переменных, заданной как z = f(x, y) .

Записывается двойной интеграл так:

.

Здесь D – плоская фигура, ограниченная линиями, выражения которых (равенства) даны в задании вычисления двойного интеграла. Слева и справа – равенствами, в которых слева переменная x , а сверху и снизу – равенствами, в которых слева переменная y . Это место и далее – одно из важнейших для понимания техники вычисления двойного интеграла.

Вычислить двойной интеграл — значит найти число, равное площади упомянутой фигуры D .

Пока мы не касаемся определения двойного интеграла, а будем учиться его вычислять. Понять, что такое двойной интеграл, проще, когда решены несколько задач на его вычисление, поэтому определение двойного интеграла вы найдёте в конце этого урока. Чуть забегая вперёд, можно лишь отметить, что определение двойного интеграла также связано с упоминавшейся фигурой D .

В случае если фигура D представляет собой прямоугольник, все линии, ограничивающие её – это прямые линии. Если фигура D — криволинейна, то слева и справа она ограничена прямыми, а сверху и снизу – кривыми линиями, заданными равенствами, которые даны в задании. Бывают и случаи, когда фигура D – треугольник, но о таких случаях чуть дальше.

Для вычисления двойного интеграла нужно, таким образом, рассортировать линии, огранивающие фигуру D , которая имеет строгое название – область интегрирования. Рассортировать на левые и правые и на верхние и нижние. Это потребуется при сведении двойного интеграла к повторному интегралу – методе вычисления двойного интеграла.

Случай прямоугольной области:

Случай криволинейной области:

А это уже решение знакомых нам определённых интегралов, в которых заданы верхний и нижний пределы интегрирования. Выражения, задающие линии, которые ограничивают фигуру D , будут пределами интегрирования для обычных определённых интегралов, к которым мы уже подходим.

Сведение двойного интеграла к повторному

Случай прямоугольной области

Пусть дана функция двух переменных f(x, y) и ограничения для D : D = <(x; y) | a ≤ x ≤ b; c ≤ y ≤ d> , означающие, что фигуру D слева и справа ограничивают прямые x = a и x = b , а снизу и сверху — прямые y = c и y = d . Здесь a, b, c, d — числа.

Пусть для такой функции существует двойной интеграл

.

Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид

.

Здесь пределы интегрирования a, b, c, d — числа, о которых только что упоминалось.

Сначала нужно вычислять внутренний (правый) определённый интеграл, затем — внешний (левый) определённый интеграл.

Можно и поменять ролями x и y. Тогда повторный интеграл будет иметь вид

.

Такой повторный интеграл нужно решать точно так же: сначала — внутренний (правый) интеграл, затем — внешний (левый).

Пример 1. Вычислить двойной интеграл

,

.

Решение. Сводим данный двойной интеграл к повторному интегралу

.

На чертеже строим область интегрирования:

Вычисляем внутренний (правый) интеграл, считая игрек константой. Пользуемся формулой 7 из таблицы интегралов. Получаем.

.

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого), пользуясь для каждого слагаемого той же формулой 7:

Результат и будет решением данного двойного интеграла.

Пример 2. Вычислить двойной интеграл

,

.

Решение. Сводим данный двойной интеграл к повторному интегралу

.

На чертеже строим область интегрирования:

Вычисляем внутренний (правый) интеграл, считая икс константой. Пользуясь формулой 9 из таблицы неопределенных интегралов, получаем

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого). Пользуемся формулой 10 из таблицы неопределенных интегралов и формулой Ньютона-Лейбница для вычисления определенного интеграла:

Результат и будет решением данного двойного интеграла.

Случай криволинейной или треугольной области

Пусть снова дана функция двух переменных f(x, y) , а ограничения для D : уже несколько другого вида:

.

Эта запись означает, что фигуру D слева и справа ограничивают, как и в случае прямолинейной области — прямые x = a и x = b , но снизу и сверху — кривые, которые заданы уравнениями и . Иными словами, и — функции.

Пусть для такой функции также существует двойной интеграл

.

Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид

.

Здесь пределы интегрирования a и b — числа, а и — функции. В случае треугольной области одна из функций или — это уравнение прямой линии. Такой случай будет разобран в примере 3.

Как и в случае прямолинейной области, сначала нужно вычислять правый определённый интеграл, затем — левый определённый интеграл.

Точно так же можно поменять ролями x и y. Тогда повторный интеграл будет иметь вид

.

Такой повторный интеграл нужно решать точно так же: сначала — внутренний (правый) интеграл, затем — внешний (левый).

Пример 3. Вычислить двойной интеграл

,

.

Решение. Сводим данный двойной интеграл к повторному интегралу

.

На чертеже строим область интегрирования и видим, что она треугольная:

Вычисляем внутренний (правый) интеграл, считая икс константой. Пользуясь формулами 6 и 7 из таблицы неопределенных интегралов, получаем

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого). Сначала представляем этот интеграл в виде суммы интегралов:

.

Вычисляем второе слагаемое, пользуясь все той же формулой:

Вычисляем третье слагаемое, также по формуле 7:

Получаем сумму, которая и будет решением данного двойного интеграла:

.

Пример 4. Вычислить двойной интеграл

,

.

Решение. Сводим данный двойной интеграл к повторному интегралу

.

На чертеже строим область интегрирования:

Пользуясь формулой Ньютона-Лейбница, вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.

.

Теперь, пользуясь формулой 7 из таблицы неопределенных интегралов, вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):

Результат и будет решением данного двойного интеграла.

Вычислить двойной интеграл самостоятельно, а затем посмотреть решение

Пример 5. Вычислить двойной интеграл

,

если область D ограничена прямыми

.

Пример 6. Вычислить двойной интеграл

,

если область D ограничена прямыми

.

x-правильная и неправильная, y-правильная и неправильная области интегрирования

Случается, область интегрирования двойного интеграла ограничена такими линиями, что возникает необходимость разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно. Это случаи, когда:

1) область интегрирования представляет собой фигуру, имеющую в виде нижней или верхней (левой или правой) границы две или более двух прямых или кривых линий;

2) область интегрирования представляет собой фигуру, границу которой прямые пересекают более чем в двух точках.

Если вышесказанное относится к левой или правой границе области интегрирования, то есть ограничениях, заданных линиями, выраженными через x, то область интегрирования называется x-неправильной. Если же прямая y = y 0 пересекает соответствующую границу лишь в одной точке и если границей служит лишь одна прямая или кривая, то область интегрирования называется x-правильной

Аналогично, если границу, заданную линиями, выраженными через y, прямая x = x 0 пересекает более чем в одной точке или если границей служат более одной прямой или кривой, то область интегрирования называется y-неправильной. Вывести теперь признаки y-правильной области, надо полагать, совсем просто.

До сих пор мы рассматривали примеры с x-неправильными и y-правильными областями интегрирования. Теперь рассмотрим случаи, когда условие правильности нарушается.

Пример 7. Вычислить двойной интеграл , область интегрирования которого ограничена линиями y = x , xy = 1 , y = 2 .

Решение. Область интегрирования является y-неправильной, так как её нижнюю границу нельзя задать одной линией y = y(x) . Как видно на рисунке выше, нижняя граница складывается из y = x (тёмно-бордовая) и xy = 1 (зелёная). Поэтому прямой x = 1 (чёрная) можем разбить область интегрирования на две части — и .

Вычисляется этот двойной интеграл так:

Смена порядка интегрирования

Как уже отмечалось выше, после приведения двойного интеграла к повторному интегралу, можно поменять переменные x и y ролями, или, говоря иначе, поменять порядок интегрирования.

Смена порядка интегрирования образно может быть описана следующими словами О’Генри: «Так ведёт себя обитатель джунглей — зверь, попав в клетку, и так ведёт себя обитатель клетки — человек, заблудившись в джунглях сомнений». Результат, так же по О’Генри один и тот же: «Чалмерс разорвал письмо на тысячу мельчайших клочков и принялся терзать свой дорогой ковёр, расхаживая по нему взад и вперёд». (О’Генри. Шехерезада с Мэдисон-сквера.)

Тогда, если левый интеграл у нас по переменной x, а правый — по y, то после смены порядка интегрирования всё будет наоборот. Тогда пределы интегрирования для «нового» игрека нужно «позаимствовать» у «старого» икса, а пределы интегрирования для «нового» икса получить в виде обратной функции, разрешив относительно икса уравнение, задававшее предел для игрека.

Пример 8. Сменить порядок интегрирования для повторного интеграла

.

Решение. После смены порядка интегрирования интеграл по игреку станет левым, а интеграл по иксу — правым. Пределы интегрирования для «нового» игрека позаимствуем у «старого» икса, то есть нижний предел равен нулю, а верхний — единице. Пределы интегрирования для «старого» игрека заданы уравнениями и . Разрешив эти уравнения относительно икса, получим новые пределы интегрирования для икса:

(нижний) и (верхний).

Таким образом, после смены порядка интегрирования повторный интеграл запишется так:

.

После смены порядка интегрирования в двойном интеграле нередко область интегрирования превращается в y-неправильную или x-неправильную (см. предыдущий параграф). Тогда требуется разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно.

Поскольку разбиение области интегрирования на части представляет определённые трудности для многих студентов, то не ограничимся примером, приведённым в предыдущем параграфе, а разберём ещё пару примеров.

Пример 9. Сменить порядок интегрирования для повторного интеграла

.

Решение. Итак, область интегрирования данного повторного интеграла ограничена прямыми y = 1 , y = 3 , x = 0 , x = 2y .

При интегрировании в другом порядке нижняя граница области состоит из двух прямых: AB и BC , которые заданы уравнениями y = 1 и y = x/2 , что видно на рисунке ниже.

Выход из такой неопределённости состоит в разбиении области интегрирования на две части. Делить область интегрирования будет прямая BМ . Новые пределы интегрирования вычисляем, находя обратную функцию. Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме двух интегралов:

Естественно, таким же будет решение двойного интеграла, который сводится к повторному интегралу, данному в условии этого примера.

Пример 10. Сменить порядок интегрирования для повторного интеграла

.

Решение. Итак, область интегрирования повторного интеграла ограничена прямыми x = 0 , x = 2 и кривыми и .

Как видно на рисунке ниже, прямая, параллельная оси 0x , будет пересекать нижнюю границу области интегрирования более чем в двух точках.

Поэтому разобьём область интегрирования на три части прямыми, которые на рисунке начерчены чёрным. Новые пределы интегрирования вычисляем, находя обратную функцию. Пределы для трёх новых областей интегрирования будут следующими.

Для :

Для :

Для :

Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме трёх интегралов:

Той же сумме трёх интегралов будет равен и двойной интеграл, который сводится к повторному интегралу, данному в условии этого примера.

И всё же обстоятельства непреодолимой силы нередко мешают студентам уже на предыдущем шаге — расстановке пределов интегрирования. Тревога и смятение не лишены некоторого основания: если для разбиения области интегрирования на части обычно достаточно приглядеться к чертежу, а для решения повторного интеграла — таблицы интегралов, то в расстановке пределов интегрирования нужен некоторый опыт тренировок. Пробежим пример, в котором остановимся только на расстановке пределов интегрирования и — почти на автомате — на разбиении области и опустим само решение.

Пример 11. Найти пределы интегрирования двойного интеграла, если область интегрирования D задана следующим образом:

Решение. В явном виде (через x и y «без примесей») линии, ограничивающие область интегрирования, не заданы. Так как для икса ими чаще всего оказываются прямые, касающиеся в одной точке верхней и нижней границ, выраженных через игрек, то пойдём именно по этому пути. Тем более, что при смене порядка интегирования мы получим область интегрирования с такой же площадью. Разрешим неравенства относительно игрека и получим:

Строим полученные линии на чертёже. Пределами интегрирования по иксу действительно служат линии x = 0 и x = 2 . Но область интегрирования оказалась y-неправильной, так как её верхнюю границу нельзя задать одной линией y = y(x) .

Поэтому разобьём область интегрирования на две части при помощи прямой x = 1 (на чертеже — чёрного цвета).

Теперь данный двойной интеграл можем записать как сумму двух повторных интегралов с правильно расставленными пределами интегрирования:

.

Вычисление площади и объёма с помощью двойных интегралов

В этом параграфе даны примеры, в которых двойной интеграл равен отрицательному числу. Но, как отмечалось в теоретической справке в начале урока, площадь области интегрирования равна самому двойному интегралу. А если двойной интеграл — отрицательное число, то площадь равна его модулю.

Вычисление площади плоской фигуры с помощью двойного интеграла имеет более универсальный характер, чем вычисление площади криволинейной трапеции с помощью определённого интеграла. С помощью двойного интеграла можно вычислять площади не только криволинейной трапеции, но и фигур, расположенных произвольно по отношению к к координатным осям.

Пример 12. Вычислить площадь области, ограниченной линиями y² = x + 1 и x + y = 1 .

Решение. Область интегрирования представляет собой фигуру, ограниченную слева параболой y² = x + 1 , а справа прямой y = 1 — x . (рисунок ниже).

Решая как систему уравнения этих линий, получаем точки их пересечения: . Ординаты этих точек — — 2 и 1 будут соответственно нижним и верхним пределами интегрирования по игреку. Итак, площадь фигуры найдём как двойной интеграл, сведённый к повторному:

.

Вычисляем внутренний (правый) интеграл:

.

Вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):

Как видим, решение двойного интеграла — отрицательное число. За площадь данной плоской фигуры принимается модуль этого числа, то есть 4/9.

Объём криволинейного цилиндра, ограниченного сверху поверхностью , снизу плоскостью z = 0 и с боковых сторон цилиндрической поверхностью, у которой образующие параллельны оси 0z , а направляющей служит контур области, вычисляется также по формуле двойного интеграла. То есть, с помощью двойного интеграла можно вычислять объёмы тел.

Пример 13. Вычислить объём тела, ограниченного поверхностями x = 0 , y = 0 , z = 0 и x + y + z = 1 (рисунок ниже).

Расставляя пределы интегрирования, получаем следующий повторный интеграл:

.

Вычисляем внутренний (правый) интеграл:

.

Вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):

Вновь видим, что решение двойного интеграла — отрицательное число. За объём данного тела принимается модуль этого числа, то есть 1/6.

Так что же такое двойной интеграл?

Мы уже знаем, что представляет собой область D. Пусть z = f(x, y) — некоторая функция двух переменных, определённая и ограниченная в этой области. Разобъём область D произвольно на n частей, не имеющих общих точек, с площадями . В каждой из этих частей выберем произвольную точку и составим сумму

,

которую назовём интегральной суммой. Диаметром области D условимся называть наибольшее расстояние между граничными точками этой области. Учитывается также наибольший из диаметров частичных областей.

Определение. Если интегральная сумма при неограниченном возрастании числа n разбиений области D и стремлении наибольшего из диаметров частичных областей к нулю имеет предел, то этот предел называется двойным интегралом от функции f(x, y) по области D.

Если областью интегрирования является окружность или часть окружности, то двойной интеграл проще вычислить в полярных координатах. Обобщением понятия двойного интеграла для функции трёх переменных является тройной интеграл.

Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам

Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам

1. Услуги проектирования
2. Двойной интеграл
3. Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам

Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам

Смысл этих задач — научиться быстро определять параметры $a,\;b,\;\varphi _1 (x),\;\varphi _2 (x),\;c,\;d,\;\psi _1 (y),\;\psi _2 (y)$ < в декартовых координатах >и $\varphi _0 ,\;\varphi _2 ,\;r_1 (\varphi ),\;r_2 (\varphi )$ < в полярных координатах >, необходимые для перехода от двойного интеграла к повторному.

Примеры:

Пусть область $D=\left[< x\leqslant 0,\;y\leqslant 0,\;x^2+y^2\leqslant 4 >\right]\cup \left[< x\geqslant 0,\;x^2+y^2\leqslant -2y >\right]$. Представить двойной интеграл по области $\mathbf < \textit < D >> $ в виде повторных. Перейти к полярным координатам. 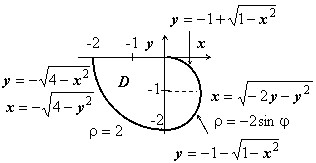Решение:

Область изображена на рисунке. Для левой части $D-2\leqslant x\leqslant 0;\quad -\sqrt < 4-x^2 >\leqslant y\leqslant 0$; для правой — $0\leqslant x\leqslant 1,\;-1-\sqrt < 1-x^2 >\leqslant y\leqslant -1+\sqrt < 1-x^2 >$ уравнение правой полуокружности после выделения полных квадратов принимает вид $x^2+(y+1)^2=1$, поэтому

Изменить порядок интегрирования, перейти к полярным координатам. 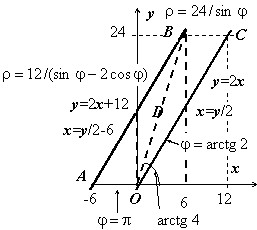$I=\int\limits_ < -6 >^0 < dx\int\limits_0^ < 2x+12 > < f(x,y)dy >> +\int\limits_0^6 < dx\int\limits_ < 2x >^ < 2x+12 > < f(x,y)dy >> +\int\limits_6^ < 12 > < dx\int\limits_ < 2x >^ < 24 > < f(x,y)dy >> $

Решение:

На рисунке изображена область и приведены уравнения прямых и обратных функций для линий, ограничивающих её. $\mathbf < \textit < D >> $ можно представить в виде $D=\left[< 0\leqslant y\leqslant 24,\;y/2-6\leqslant x\leqslant y/2 >\right]$, поэтому $I=\int\limits_0^ < 24 > < dy\int\limits_ < y/2-6 >^ < y/2 > < f(x,y)dx >> $. В полярных координатах $\mathbf < \textit < D >> $ представляется как объединение двух треугольников $\mathbf < \textit < OCB >> $и $\mathbf < \textit < OBA >> $. Уравнение прямой $\mathbf < \textit < ОС >> $: $\varphi =arctg2$ < можно получить и формально, перейдя к полярным координатам в её уравнении: $y=2x\Rightarrow \quad r\sin \varphi =2r\cos \varphi \Rightarrow tg\varphi =2$ >, прямой $\mathbf < \textit < ОВ >> $: $\varphi =arctg4$, прямой $\mathbf < \textit < СВ >> $: $y=24\Rightarrow r\sin \varphi =24\Rightarrow \quad r=24/\sin \varphi $, прямой $\mathbf < \textit < ОА >> $: $\varphi =\pi $, прямой $\mathbf < \textit < АВ >> $: $y=2x+12\Rightarrow r\sin \varphi =2r\cos \varphi +12\Rightarrow \quad r=\frac < 12 > < \sin \varphi -2\cos \varphi >$.

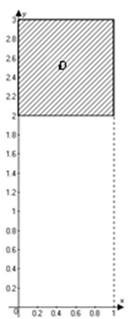
Вычислить двойной интеграл $\iint\limits_ < D > < \left( 6x < < y >^ < 2 >> -12 < < x >^ < 2 >> y \right)dxdy > $, где область $D$ – квадрат со сторонами $x=0$, $x=1$, $y=2$, $y=3$. В повторном интеграле внутренний интеграл вначале вычислить по переменной $y$, а внешний – по $x$. Вычислить этот же интеграл, изменив порядок интегрирования.

Решение:

Вначале изобразим область интегрирования. Запишем заданный двойной интеграл через повторные: $\iint\limits_ < D > < \left( 6x < < y >^ < 2 >> -12 < < x >^ < 2 >> y \right)dxdy > =\int\limits_ < 0 >^ < 1 > < dx >\int\limits_ < 2 >^ < 3 > < \left( 6x < < y >^ < 2 >> -12 < < x >^ < 2 >> y \right)dy > $.

Внутреннее < первое >интегрирование будем выполнять по переменной $y$ < при этом считаем, что $x$ – константа >, а внешнее < второе >– по переменной $x$:

$$=\int\limits_ < 0 >^ < 1 > < 38xdx >-\int\limits_ < 0 >^ < 1 > < 30 < < x >^ < 2 >> dx > =38\int\limits_ < 0 >^ < 1 > < xdx >-30\int\limits_ < 0 >^ < 1 > < < < x >^ < 2 >> dx > =38\cdot \left. \frac < < < x >^ < 2 >> > < 2 >\right|_ < 0 >^ < 1 >-30\cdot \left. \frac < < < x >^ < 3 >> > < 3 >\right|_ < 0 >^ < 1 >=$$

Вычислим теперь заданный по условию двойной интеграл, сменив порядок интегрирования: внутреннее интегрирование будем проводить по переменной $x$ < считая, что $y$ есть постоянной >, а внешнее – по переменной $y$:

$$=\int\limits_ < 2 >^ < 3 > < \left[ 6 < < y >^ < 2 >> \int\limits_ < 0 >^ < 1 > < xdx >-12y\int\limits_ < 0 >^ < 1 > < < < x >^ < 2 >> dx >\right]dy > =\int\limits_ < 2 >^ < 3 > < \left[ 6 < < y >^ < 2 >> \cdot \left. \frac < < < x >^ < 2 >> > < 2 >\right|_ < 0 >^ < 1 >-12y\cdot \left. \frac < < < x >^ < 3 >> > < 3 >\right|_ < 0 >^ < 1 >\right]dy > =$$

$$=\int\limits_ < 2 >^ < 3 > < \left( 3 < < y >^ < 2 >> -4y \right)dy > =\left. \left( 3\cdot \frac < < < y >^ < 3 >> > < 3 >-4\cdot \frac < < < y >^ < 2 >> > < 2 >\right) \right|_ < 2 >^ < 3 >=27-8-2\left( 9-4 \right)=19-10=9$$

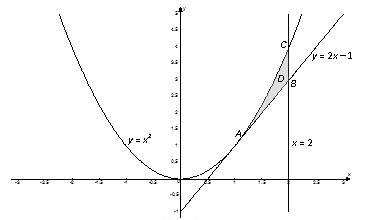
Вычислить двойной интеграл $\iint\limits_ < D > < \left( < < x >^ < 2 >> +2y \right)dxdy > $, если область $D$ ограничена линиями $y= < < x >^ < 2 >> $, $x=2$, $y=2x-1$. Вычислить этот же интеграл, изменив порядок интегрирования.

Решение:

Строим заданную область $D$. Вначале внутреннее интегрирование будем проводить по переменной $y$, а внешнее – по $x$: $$\iint\limits_ < D > < \left( < < x >^ < 2 >> +2y \right)dxdy > =\int\limits_ < a >^ < b > < dx >\int\limits_ < < < \phi >_ < 1 >> \left( x \right) > ^ < < < \phi >_ < 2 >> \left( x \right) > < \left( < < x >^ < 2 >> +2y \right)dy > $$

Контур области $D$ пересекается любой прямой, параллельной оси ординат, в двух точках.

Найдем пределы интегрирования. Переменная $x$ изменяется от абсциссы точки $A$ к абсциссе точек $B$ и $C$. Координаты точки $A$ найдем как координаты точки пересечения графиков функций $y= < < x >^ < 2 >> $ и $y=2x-1$:

$$\left[ \begin < matrix >y= < < x >^ < 2 >> , \\ y=2x-1 \\ \end < matrix >\right.\Rightarrow < < x >^ < 2 >> =2x-1\Rightarrow < < x >^ < 2 >> -2x+1=0\Rightarrow < < \left( x-1 \right) >^ < 2 >> =0\Rightarrow < < x >_ < A >> =1$$

Так как точки $B$ и $C$ лежать на прямой $x=2$, то $ < < x >_ < B >> = < < x >_ < C >> =2$. Итак, $1\le x\le 2$. Далее на отрезке $\left[ 1;\ 2 \right]$ выбираем произвольную точку $x$, через нее проводим прямую, параллельную оси $Oy$, и на этой прямой рассмотрим отрезок $KL$, принадлежащий области $D$.

Область $D$ ограничена снизу прямой $y=2x-1$, а сверху – веткой параболы $y= < < x >^ < 2 >> $. Переменная $y$ изменяется в заданной области $D$ от ее значения $2x-1$ на нижней части контура $ABC$ до ее значения $ < < x >^ < 2 >> $ на верхней части этого контура.

Замечание. Уравнения линий, ограничивающих контур, должны быть разрешены относительно той переменной, относительно которой находится внутренний интеграл.

Таким образом, $2x-1\le y\le < < x >^ < 2 >> $, а тогда область $D$ задается следующими неравенствами:

$$D:\left[ \begin < matrix >1\le x\le 2, \\ 2x-1\le y\le < < x >^ < 2 >> . \\ \end < matrix >\right.$$

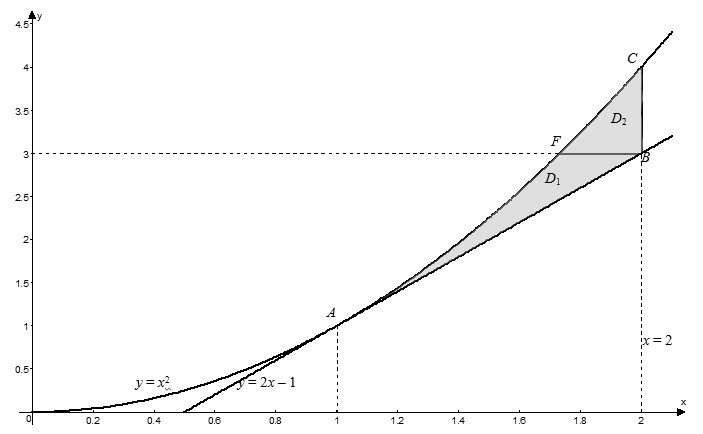
Вычислим теперь рассматриваемый двойной интеграл, изменив порядок интегрирования: внутреннее интегрирование будем проводить по переменной $x$, а внешнее – по $y$. То есть, перейдя к повторным интегралам, получим:

$$\iint\limits_ < D > < \left( < < x >^ < 2 >> +2y \right)dxdy > =\int\limits_ < c >^ < d > < dy >\int\limits_ < < < \psi >_ < 1 >> \left( y \right) > ^ < < < \psi >_ < 2 >> \left( y \right) > < \left( < < x >^ < 2 >> +2y \right)dx > $$ 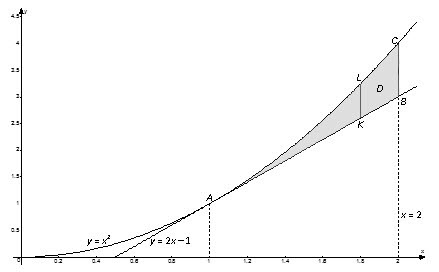Из рисунка в области $D$ видно, что левая граница контура области – одна линия < положительная ветка параболы $y= < < x >^ < 2 >> $), а его правая часть состоит из двух линий $AB$ < отрезок прямой $y=2x-1$) и $BC$ < отрезок прямой $x=2$), то есть задается разными уравнениями. В этом случае область $D$ нужно разбить на части так, чтобы каждая из них справа была ограничена только одной линией. В данном случае такими частями будут $ < < D >_ < 1 >> -ABF$ и $ < < D >_ < 2 >> -BCF$. Заданная область $D$ будет суммой областей $ < < D >_ < 1 >> $ и $ < < D >_ < 2 >> $. Тогда искомый интеграл будет равен сумме интегралов по каждой из областей:

$$\iint\limits_ < D > < \left( < < x >^ < 2 >> +2y \right)dxdy > =\iint\limits_ < < < D >_ < 1 >> > < \left( < < x >^ < 2 >> +2y \right)dxdy > +\iint\limits_ < < < D >_ < 2 >> > < \left( < < x >^ < 2 >> +2y \right)dxdy > $$

Поскольку в данном случае внутреннее интегрирование проводится по переменной $x$, то уравнения ограничивающих линий нужно разрешить относительно этой переменной:

$$AB:y=2x-1\Rightarrow x=\frac < y+1 > < 2 >; \qquad AC:y= < < x >^ < 2 >> \Rightarrow x=\sqrt < y >$$

Найдем пределы интегрирования для каждой из областей. В области $ < < D >_ < 1 >> $ переменная $y$ изменяется от ординаты точки $A$ до ординат точек $B$ и $F$. Точка $A$ принадлежит параболе $y= < < x >^ < 2 >> $ и выше было найдено, что абсцисса этой точки $ < < x >_ < A >> =1$, тогда $ < < y >_ < A >> = < < 1 >^ < 2 >> =1$. Точка $B$ – точка пересечения двух прямых $x=2$ и $y=2x-1$, а тогда $ < < y >_ < B >> =2\cdot 2-1=3$. Итак имеем, что $1\le y\le 3$. Переменная $x$ в области $ < < D >_ < 1 >> $ изменяется от ветки параболы $x=\sqrt < y >$ до прямой $x=\frac < y+1 > < 2 >$, то есть $ < < D >_ < 1 >> :\left[ \begin < matrix >1\le y\le 3, \\ \sqrt < y >\le x\le \frac < y+1 > < 2 >. \\ \end < matrix >\right.$ Аналогично для области $ < < D >_ < 2 >> $ находим, что $ < < D >_ < 2 >> :\left[ \begin < matrix >3\le y\le 4, \\ \sqrt < y >\le x\le 2. \\ \end < matrix >\right.$

Вычислить двойной интеграл (\iint\limits_R < \left( < < x^2 >+ < y^2 >>\right)dydx > ,) преобразовав его в полярные координаты. Область интегрирования (R) представляет собой сектор (0 \le \theta \le \large\frac < \pi > < 2 >\normalsize) круга радиусом (r = \sqrt 3.)

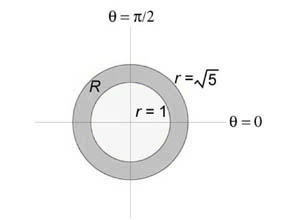
Вычислить интеграл (\iint\limits_R < xydydx >,) в котором область интегрирования (R) представляет собой кольцо, ограниченное окружностями ( < x^2 >+ < y^2 >= 1) и ( < x^2 >+ < y^2 >= 5.)

Решение:

В полярных координатах область интегрирования (R) является полярным прямоугольником: $R = \left( < \left( < r,\theta >\right)|\;1 \le r \le \sqrt 5 ,0 \le \theta \le 2\pi >\right).$

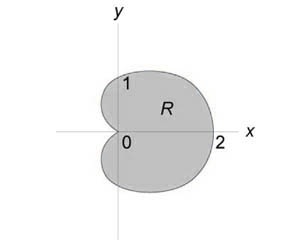
Найти интеграл (\iint\limits_R < \sin \theta drd\theta >,) где область интегрирования (R) ограничена кардиоидой (r = 1 + \cos \theta ).

Решение:

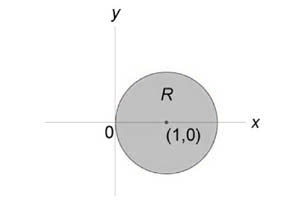
Вычислить интеграл (\iint\limits_R < \left( < < x^2 >+ < y^2 >>\right)dxdy > ) в круге ( < x^2 >+ < y^2 >= 2x.)

Решение: Область интегрирования (R) показана на рисунке:

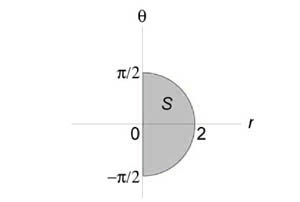
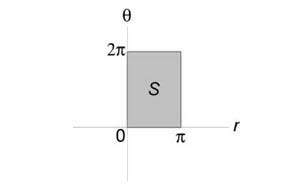
Преобразуем уравнение окружности следующим образом: $ < < x^2 >+ < y^2 >= 2x, > \;\; < \Rightarrow < x^2 >— 2x + 1 + < y^2 >= 1, > \;\; < \Rightarrow < \left( < x - 1 >\right)^2 > + < y^2 >= 1. > $ Подставляя (x = r\cos \theta ,) (y = r\sin \theta ,) найдем уравнение окружности в полярных координатах. $ < < x^2 >+ < y^2 >= 2x, > \;\; < \Rightarrow < r^2 > < \cos ^2 >\theta + < r^2 > < \sin^2 >\theta = 2r\cos \theta , > \;\; < \Rightarrow < r^2 >\left( < < < \cos >^2 > \theta + < \sin^2 >\theta >\right) = 2r\cos \theta , > \;\; < \Rightarrow r = 2\cos \theta . >$ Образ (S) области интегрирования (R) показан на рисунке:

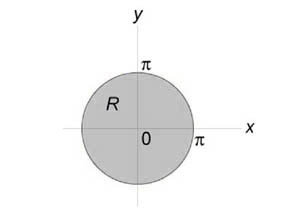
Вычислить двойной интеграл (\iint\limits_R < \sin \sqrt < < x^2 >+ < y^2 >> dxdy > ) посредством преобразования в полярные координаты. Область интегрирования (R) представляет собой круг ( < x^2 >+ < y^2 >\le < \pi ^2 >.)

Решение:

Область интегрирования (R) представлена на рисунке:

Образ (S) данной области описывается множеством (\left[< S = \left( < r,\theta >\right)|\;0 \le r \le \pi ,0 \le \theta \le 2\pi >\right]) и показан на рисунке:

Далее:

Свойства тройного интеграла

СКНФ. Теорема о представлении в виде СКНФ. Построение СКНФ по таблице

Теорема об аналоге СДНФ в Pk

Вычисление тройного интеграла. Теорема о переходе от тройного интеграла к повторному

Вычисление площади поверхности

Формула Гаусса — Остроградского

Булевы функции от $n$ переменных

Инвариантное определение дивергенции

СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице

Замена переменных в тройном интеграле

Дифференциальные характеристики векторного поля

Критерий полноты

Вычисление двойного интеграла

Формулы. Равенство функций и эквивалентность формул. Основные эквивалентности

Теорема Остроградского

Огравление $\Rightarrow $