Для эконометрической модели уравнения регрессии

Тема 4: Линейное уравнение множественной регрессии

1. Для регрессионной модели зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х₁) и уровня безработицы в субъекте (%, х₂) получено уравнение . Величина коэффициента регрессии при переменной х₂ свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.

изменится на (-1,67)

увеличится на 1,67

уменьшится на (-1,67)

изменится на 0,003

Решение:

Эконометрическая модель линейного уравнения регрессии имеет вид , где y – зависимая переменная, x_j – независимая переменная ( – номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, b_j – параметры уравнения; – ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Коэффициентом регрессии является параметр b_j. Его величина показывает, на сколько в среднем изменится зависимая переменная y, при изменении соответствующей независимой переменной x_j на 1 единицу измерения. Таким образом, при изменении уровня безработицы на 1% среднедушевой денежный доход изменится на (-1,67) рубля при неизменной величине валового регионального продукта.

2. В уравнении линейной множественной регрессии: , где – стоимость основных фондов (тыс. руб.); – численность занятых (тыс. чел.); y – объем промышленного производства (тыс. руб.) параметр при переменной х₁, равный 10,8, означает, что при увеличении объема основных фондов на _____ объем промышленного производства _____ при постоянной численности занятых.

на 1 тыс. руб. … увеличится на 10,8 тыс. руб.

на 1 тыс. руб. … уменьшится на 10,8 тыс. руб

на 1 тыс. руб. … увеличится на 10,8%

на 1% … увеличится на 10,8%

Решение:

В уравнении множественной линейной регрессии , параметр показывает среднее изменение результата y при увеличении фактора на одну единицу, при условии, что все остальные переменные останутся на постоянном уровне. В нашем случае, объем промышленного производства y характеризуется следующим уравнением , параметр равен 10,8, следовательно, при увеличении объема основных фондов на 1 тыс. руб. объем промышленного производства увеличится на 10,8 тыс. руб. при постоянной численности занятых.

3. Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …

Решение:

Коэффициент детерминации равен доле дисперсии, объясненной регрессией, в общей дисперсии. Величина ( ) показывает долю остаточной дисперсии в общей или дисперсию, вызванную влиянием остальных, не учтенных в модели факторов.
. Значит,

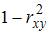
4. Построена эконометрическая модель для зависимости прибыли от реализации единицы продукции (руб., у) от величины оборотных средств предприятия (тыс. р., х₁): . Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет _____ рубля.

Решение:

Эконометрическая модель линейного уравнения парной регрессии имеет вид: , где y – зависимая переменная, x – независимая переменная; a, b – параметры уравнения; – ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Значение параметра а может быть рассчитано по формуле . Если , то ; в таком случае говорят, что среднее значение переменной y, не зависящее от величины переменной х, равно значению параметра а. Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет 10,75 рубля.

5. F-статистика рассчитывается как отношение ______ дисперсии к ________ дисперсии, рассчитанных на одну степень свободы.

факторной … к общей

Решение:

F-статистика рассчитывается как отношение факторной дисперсии на одну степень свободы к остаточной дисперсии на одну степень свободы.

Тема 5: Оценка параметров линейных уравнений регрессии

1. Для эконометрической модели уравнения регрессии ошибка модели определяется как ______ между фактическим значением зависимой переменной и ее расчетным значением.

сумма квадратов разности

сумма разности квадратов

Решение:

Одним из типов эконометрических моделей является уравнение регрессии, которое может быть записано в виде математического выражения , где y – зависимая переменная; x_j – независимая переменная (j = 1,…, k; k – количество независимых переменных); f – тип функциональной зависимости (математическая функция); – случайные факторы. При этом , тогда , где – фактическое значение зависимой переменной, – расчетное значение зависимой переменной, – ошибка модели. Выразим значение : . Поэтому правильный ответ – «разность».

2. Величина называется …

Решение:

Величина называется случайной составляющей, или возмущением, и включает в себя влияние факторов, неучтенных в модели, ошибок выборки и ошибок измерения.

3. В эконометрической модели уравнения регрессии величина отклонения фактического значения зависимой переменной от ее расчетного значения характеризует …

величину коэффициента регрессии

значение свободного члена уравнения

нулевое значение независимой переменной

Решение:

Одним из типов эконометрических моделей является уравнение регрессии, которое может быть записано в виде математического выражения , где y – зависимая переменная; x_j – независимая переменная (j = 1,…, k; k – количество независимых переменных); f – тип функциональной зависимости (математическая функция); – случайные факторы. При этом , тогда , где – фактическое значение зависимой переменной, – расчетное значение зависимой переменной, – ошибка модели. Поэтому правильный ответ – «ошибку модели».

4. Известно, что доля объясненной дисперсии в общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …

Решение:

Коэффициент детерминации равен доле дисперсии, объясненной регрессией, в общей дисперсии. Следовательно,

5. При методе наименьших квадратов параметры уравнения парной линейной регрессии определяются из условия ______ остатков .

Уравнение множественной регрессии

Назначение сервиса . С помощью онлайн-калькулятора можно найти следующие показатели:

• уравнение множественной регрессии, матрица парных коэффициентов корреляции, средние коэффициенты эластичности для линейной регрессии;
• множественный коэффициент детерминации, доверительные интервалы для индивидуального и среднего значения результативного признака;

Кроме этого проводится проверка на автокорреляцию остатков и гетероскедастичность.

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Отбор факторов обычно осуществляется в два этапа:

1. теоретический анализ взаимосвязи результата и круга факторов, которые оказывают на него существенное влияние;
2. количественная оценка взаимосвязи факторов с результатом. При линейной форме связи между признаками данный этап сводится к анализу корреляционной матрицы (матрицы парных линейных коэффициентов корреляции). Научно обоснованное решение задач подобного вида также осуществляется с помощью дисперсионного анализа — однофакторного, если проверяется существенность влияния того или иного фактора на рассматриваемый признак, или многофакторного в случае изучения влияния на него комбинации факторов.

Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.
2. Каждый фактор должен быть достаточно тесно связан с результатом (т.е. коэффициент парной линейной корреляции между фактором и результатом должен быть существенным).
3. Факторы не должны быть сильно коррелированы друг с другом, тем более находиться в строгой функциональной связи (т.е. они не должны быть интеркоррелированы). Разновидностью интеркоррелированности факторов является мультиколлинеарность — тесная линейная связь между факторами.

Пример . Постройте регрессионную модель с 2-мя объясняющими переменными (множественная регрессия). Определите теоретическое уравнение множественной регрессии. Оцените адекватность построенной модели.
Решение.
К исходной матрице X добавим единичный столбец, получив новую матрицу X

1	5	14.5
1	12	18
1	6	12
1	7	13
1	8	14

Матрица Y

9

13

16

14

21

Транспонируем матрицу X, получаем X T :

1	1	1	1	1
5	12	6	7	8
14.5	18	12	13	14

Умножаем матрицы, X T X =

5 38 71,5 38 318 563,5 71,5 563,5 1043,25

В матрице, (X T X) число 5, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы X T и 1-го столбца матрицы X

Умножаем матрицы, X T Y =

73 563 1032,5

Находим обратную матрицу (X T X) -1

13.99	0.64	-1.3
0.64	0.1	-0.0988
-1.3	-0.0988	0.14

Вектор оценок коэффициентов регрессии равен

(X T X) -1 X T Y = y(x) =

13,99 0,64 -1,3 0,64 0,1 -0,0988 -1,3 -0,0988 0,14

*

73 563 1032,5

=

34,66 1,97 -2,45

Получили оценку уравнения регрессии: Y = 34.66 + 1.97X₁-2.45X₂
Оценка значимости уравнения множественной регрессии осуществляется путем проверки гипотезы о равенстве нулю коэффициент детерминации рассчитанного по данным генеральной совокупности. Для ее проверки используют F-критерий Фишера.
R 2 = 1 — s 2 _e/∑(y_i — y_ср) 2 = 1 — 33.18/77.2 = 0.57
F = R 2 /(1 — R 2 )*(n — m -1)/m = 0.57/(1 — 0.57)*(5-2-1)/2 = 1.33
Табличное значение при степенях свободы k₁ = 2 и k₂ = n-m-1 = 5 — 2 -1 = 2, Fkp(2;2) = 19
Поскольку фактическое значение F = 1.33 Пример №2 . Приведены данные за 15 лет по темпам прироста заработной платы Y (%), производительности труда X₁ (%), а также по уровню инфляции X₂ (%).

Год	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
X1	3,5	2,8	6,3	4,5	3,1	1,5	7,6	6,7	4,2	2,7	4,5	3,5	5,0	2,3	2,8
X2	4,5	3,0	3,1	3,8	3,8	1,1	2,3	3,6	7,5	8,0	3,9	4,7	6,1	6,9	3,5
Y	9,0	6,0	8,9	9,0	7,1	3,2	6,5	9,1	14,6	11,9	9,2	8,8	12,0	12,5	5,7

Решение. Подготовим данные для вставки из MS Excel (как транспонировать таблицу для сервиса см. Задание №2) .

Включаем в отчет: Проверка общего качества уравнения множественной регрессии (F-статистика. Критерий Фишера, Проверка на наличие автокорреляции),

После нажатия на кнопку Дале получаем готовое решение.
Уравнение регрессии (оценка уравнения регрессии):
Y = 0.2706 + 0.5257X₁ + 1.4798X₂
Скачать.

Качество построенного уравнения регрессии проверяется с помощью критерия Фишера (п. 6 отчета).

Пример №3 .
В таблице представлены данные о ВВП, объемах потребления и инвестициях некоторых стран.

ВВП	16331,97	16763,35	17492,22	18473,83	19187,64	20066,25	21281,78	22326,86	23125,90
Потребление в текущих ценах	771,92	814,28	735,60	788,54	853,62	900,39	999,55	1076,37	1117,51
Инвестиции в текущих ценах	176,64	173,15	151,96	171,62	192,26	198,71	227,17	259,07	259,85

Решение:
Для проверки полученных расчетов используем инструменты Microsoft Excel «Анализ данных» (см. пример).

Пример №4 . На основе данных, приведенных в Приложении и соответствующих Вашему варианту (таблица 2), требуется:

1. Построить уравнение множественной регрессии. При этом признак-результат и один из факторов остаются теми же, что и в первом задании. Выберите дополнительно еще один фактор из приложения 1 (границы наблюдения должны совпадать с границами наблюдения признака-результата, соответствующего Вашему варианту). При выборе фактора нужно руководствоваться его экономическим содержанием или другими подходами. Пояснить смысл параметров уравнения.
2. Рассчитать частные коэффициенты эластичности. Сделать вывод.
3. Определить стандартизованные коэффициенты регрессии (b-коэффициенты). Сделать вывод.
4. Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделать выводы.
5. Оценить значимость параметров уравнения регрессии с помощью t-критерия Стьюдента, а также значимость уравнения регрессии в целом с помощью общего F-критерия Фишера. Предложить окончательную модель (уравнение регрессии). Сделать выводы.

Решение. Определим вектор оценок коэффициентов регрессии. Согласно методу наименьших квадратов, вектор получается из выражения:
s = (X T X) -1 X T Y
Матрица X

1	3.9	10
1	3.9	14
1	3.7	15
1	4	16
1	3.8	17
1	4.8	19
1	5.4	19
1	4.4	20
1	5.3	20
1	6.8	20
1	6	21
1	6.4	22
1	6.8	22
1	7.2	25
1	8	28
1	8.2	29
1	8.1	30
1	8.5	31
1	9.6	32
1	9	36

Матрица Y

7
7
7
7
7
7
8
8
8
10
9
11
9
11
12
12
12
12
14
14

Матрица X T

1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
3.9	3.9	3.7	4	3.8	4.8	5.4	4.4	5.3	6.8	6	6.4	6.8	7.2	8	8.2	8.1	8.5	9.6	9
10	14	15	16	17	19	19	20	20	20	21	22	22	25	28	29	30	31	32	36

Умножаем матрицы, (X T X)

Умножаем матрицы, (X T Y)

Находим определитель det(X T X) T = 139940.08
Находим обратную матрицу (X T X) -1

Уравнение регрессии
Y = 1.8353 + 0.9459X ₁ + 0.0856X ₂
Для несмещенной оценки дисперсии проделаем следующие вычисления:
Несмещенная ошибка e = Y — X*s

0.62
0.28
0.38
0.01
0.11
-1
-0.57
0.29
-0.56
0.02
-0.31
1.23
-1.15
0.21
0.2
-0.07
-0.07
-0.53
0.34
0.57

se 2 = (Y — X*s) T (Y — X*s)
Несмещенная оценка дисперсии равна

Оценка среднеквадратичного отклонения равна

Найдем оценку ковариационной матрицы вектора k = σ*(X T X) -1

k(x) = 0.36

0,619 -0,0262 -0,0183 -0,0262 0,126 -0,0338 -0,0183 -0,0338 0,0102

=

0,222 -0,00939 -0,00654 -0,00939 0,0452 -0,0121 -0,00654 -0,0121 0,00366

Дисперсии параметров модели определяются соотношением S 2 _i = K_ii, т.е. это элементы, лежащие на главной диагонали
С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле

Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции (от 0 до 1)

Связь между признаком Y факторами X сильная
Частные коэффициенты (или индексы) корреляции, измеряющие влияние на у фактора х_i при неизменном уровне других факторов определяются по стандартной формуле линейного коэффициента корреляции — последовательно берутся пары yx1,yx2. , x1x2, x1x3.. и так далее и для каждой пары находится коэффициент корреляции

Коэффициент детерминации
R 2 = 0.97 2 = 0.95, т.е. в 95% случаев изменения х приводят к изменению y. Другими словами — точность подбора уравнения регрессии — высокая

Значимость коэффициента корреляции

По таблице Стьюдента находим Tтабл: T_табл (n-m-1;a) = (17;0.05) = 1.74
Поскольку Tнабл Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно

Построение парной регрессионной модели

Рекомендации к решению контрольной работы.

Статистические данные по экономике можно получить на странице Россия в цифрах.
После определения зависимой и объясняющих переменных можно воспользоваться сервисом Множественная регрессия. Регрессионную модель с 2-мя объясняющими переменными можно построить используя матричный метод нахождения параметров уравнения регрессии или метод Крамера для нахождения параметров уравнения регрессии.

Пример №3 . Исследуется зависимость размера дивидендов y акций группы компаний от доходности акций x₁, дохода компании x₂ и объема инвестиций в расширение и модернизацию производства x₃. Исходные данные представлены выборкой объема n=50.

Тема I. Парная линейная регрессия
Постройте парные линейные регрессии — зависимости признака y от факторов x₁, x₂, x₃ взятых по отдельности. Для каждой объясняющей переменной:

1. Постройте диаграмму рассеяния (поле корреляции). При построении выберите тип диаграммы «Точечная» (без отрезков, соединяющих точки).
2. Вычислите коэффициенты уравнения выборочной парной линейной регрессии (для вычисления коэффициентов регрессии воспользуйтесь встроенной функцией ЛИНЕЙН (функция находится в категории «Статистические») или надстройкой Пакет Анализа), коэффициент детерминации, коэффициент корреляции (функция КОРЕЛЛ), среднюю ошибку аппроксимации.
3. Запишите полученное уравнение выборочной регрессии. Дайте интерпретацию найденным в предыдущем пункте значениям.
4. Постройте на поле корреляции прямую линию выборочной регрессии по точкам .
5. Постройте диаграмму остатков.
6. Проверьте статистическую значимость коэффициентов регрессии по критерию Стьюдента (табличное значение определите с помощью функции СТЬЮДРАСПОБР) и всего уравнения в целом по критерию Фишера (табличное значение F_табл определите с помощью функции FРАСПОБР).
7. Постройте доверительные интервалы для коэффициентов регрессии. Дайте им интерпретацию.
8. Постройте прогноз для значения фактора, на 50% превышающего его среднее значение.
9. Постройте доверительный интервал прогноза. Дайте ему экономическую интерпретацию.
10. Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемого фактора на показатель.

Тема II. Множественная линейная регрессия
1. Постройте выборочную множественную линейную регрессию показателя на все указанные факторы. Запишите полученное уравнение, дайте ему экономическую интерпретацию.
2. Определите коэффициент детерминации, дайте ему интерпретацию. Вычислите среднюю абсолютную ошибку аппроксимации и дайте ей интерпретацию.
3. Проверьте статистическую значимость каждого из коэффициентов и всего уравнения в целом.
4. Постройте диаграмму остатков.
5. Постройте доверительные интервалы коэффициентов. Для статистически значимых коэффициентов дайте интерпретации доверительных интервалов.
6. Постройте точечный прогноз значения показателя y при значениях факторов, на 50% превышающих их средние значения.
7. Постройте доверительный интервал прогноза, дайте ему экономическую интерпретацию.
8. Постройте матрицу коэффициентов выборочной корреляции между показателем и факторами. Сделайте вывод о наличии проблемы мультиколлинеарности.
9. Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемых факторов на показатель.

Регрессия в эконометрике

Вы будете перенаправлены на Автор24

Регрессия и ее виды

Регрессионный анализ – это основной математико-статистический инструмент в эконометрике. Регрессия представляет собой зависимость среднего значения величины $y$ от другой величины $x$ или же нескольких величин $x_i$.

Количество факторов, которые включены в равнение регрессии, определяет вид регрессии, которая может быть простой (парной) и множественной.

Простая регрессия – это модель, в которой среднее значение зависимой переменной y является функцией одной независимой переменной x.

Парная регрессия в неявном виде – это уравнение вида:

В явном виде: $y ̂= a + bx$, где $a$ и $b$ – это оценки коэффициента регрессии.

Множественной регрессией является модель, в которой среднее значение объясняемой переменной $y$ – это функция нескольких объясняющих переменных $x_1, x_2, …, x_n$. Множественная регрессия в неявном виде – это модель типа:

$y ̂= f(x_1, x_2,…, x_n)$

В явном виде: $y ̂= a + b_1x_1 + b_2x_2 + … + b_nx_n$

Примером модели множественной регрессии может выступать зависимость зарплаты работников от их возраста, уровня образования, степени квалификации, стажа работы, отрасли и т.д.

Относительно формы регрессия может быть линейной и нелинейной, предполагающей наличие нелинейных соотношений среди факторов. В большинстве случаев нелинейные модели можно привести к линейному виду.

Предпосылки регрессионного анализа

Чтобы проведение регрессионного анализа было наиболее результативным, необходимо выполнять определенные условия:

• В любом наблюдении математические ожидания случайной ошибки должны быть равны нулю;
• Дисперсия случайной ошибки для всех наблюдений должна быть постоянной;
• Случайные ошибки не должны иметь между собой статической зависимости;
• Объясняющая переменная x должна быть величиной неслучайной.

Если выполняются все вышеперечисленные условия, то модель является линейной классической регрессионной. Рассмотрим подробнее предположения и условия, составляющие основу регрессионного анализа.

Готовые работы на аналогичную тему

Согласно первому условию, случайная ошибка не должна систематически смещаться. Если в уравнении регрессии имеется постоянный член, то данное условие автоматически выполняется.

Второе условие – это наличие в каждом наблюдении только одного значения дисперсии случайной ошибки. Дисперсия – это возможное изменение случайной ошибки до проведения выборки. Величина дисперсии является неизвестной, а задача регрессионного анализа – это ее оценка. Независимость дисперсии случайных ошибок от номера наблюдения – это гомоскедастичность, т.е. одинаковый разброс. Гетероскедастичность – это зависимость дисперсии случайных ошибок от номера наблюдения.

Если не выполняется условие гомоскедастичности, то оценка коэффициентов регрессии будет неэффективной.

Третье условие состоит в некоррелированности случайных отклонений для различных наблюдений. Данное условие часто не выполняется при ситуации, когда данные – это временные ряды. Если оно не выполняется, то это означает автокорреляцию остатков. Чтобы диагностировать и устранить автокорреляцию, существуют специальные методы.

Четвертое условие представляет особую важность, поскольку если не выполняется условие неслучайности объясняющих переменных, то оценка коэффициентов регрессии будет смещенной и несостоятельной. Данное условие нарушается при ошибках в измерении объясняющих переменных или же при использовании лаговых переменных.

Парная регрессионная модель

Как правило в естественных науках рассматриваются функциональные зависимости, в которых каждое значение одной переменной соответствует единственному значению другой. Однако в экономических переменных нет таких зависимостей, но есть статистические и корреляционные зависимости.

Наибольшую опасность в парной регрессии представляют ошибки в измерениях. Если ошибки спецификации возможно уменьшить с помощью изменения формы модели, ошибки выборки – при помощи увеличения объема исходных данных, то ошибки изменения невозможно исправить.

Случайный фактор в регрессионных моделях может отсутствовать по следующим причинам:

1. В модель не включены все объясняющие переменные. Любая модель эконометрики – это упрощение реальной ситуации, которая является сложнейшим переплетением факторов, большинство из которых не учитываются в модели, из-за чего реальные значения зависимой переменной отклоняются от модельных значений. Невозможно перечислить все виды объясняющих переменных, поскольку неизвестно заранее, какие факторы относятся к определяющим, а какие можно не учитывать.
2. Неправильное определение функционального типа модели. Слабая изученность исследуемого процесса, его переменчивость влияет на правильность подбора его моделирующей функции. Это отражается и на отклонении модели от реальной жизни.
3. Агрегирование переменных. Многие модели содержат зависимость между факторами, являющимися комбинацией других переменных. Например, чтобы рассмотреть в качестве зависимой переменной совокупный спрос, необходимо провести анализ зависимости, содержащей объясняемую переменную, являющуюся композицией индивидуальных спросов, которые оказывают влияние на нее. Это может послужить причиной отклонения значений реальных от модельных.
4. Ошибки в измерениях. Даже при качественной модели ошибки в измерениях сказываются на несоответствии получаемых значений эмпирическим.
5. Ограниченность статистической информации. Часто строятся модели, которые являются непрерывными функциями. Для этого применяется информация, имеющая дискретную структуру. Данное несоответствие выражается в случайном отклонении.
6. Непредсказуемость человеческих факторов. Данная причина может исказить любую качественную эконометрическую модель, поскольку даже правильный выбор формы модели, скрупулезный подбор объясняющих переменных не позволяют спрогнозировать поведение индивидов.