Для кривой напишите уравнение нормальной плоскости

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

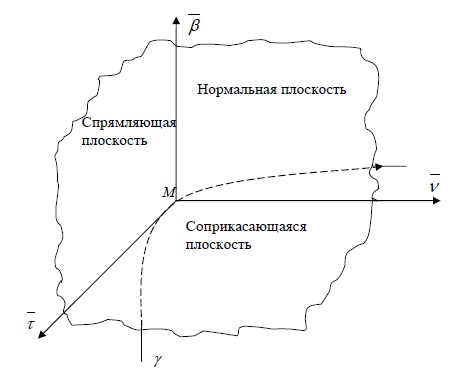
Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе

Краткие теоретические сведения

Кривая в пространстве

Рассмотрим в пространстве гладкую кривую $\gamma$.

Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:

\begin \vec=\vec(t_0), \quad x_0=x(t_0),\, y_0=y(t_0), \, z_0=z(t_0). \end

Пусть в точке $M$ $ \vec(t_0)\neq\vec<0>$, то есть $M$ не является особой точкой.

Касательная к кривой

Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $\vec(t_0)$.

Пусть $\vec$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид

Здесь $\lambda\in(-\infty,+\infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $\lambda$ будут соответствовать разные значения $\vec$).

Если $\vec=\$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:

Нормальная плоскость

Плоскость, проходящую через данную точку $M$ кривой $\gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.

Пусть $\vec$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $\vec-\vec(t_0)$ и $\vec(t_0)$:

Если расписать покоординатно, то получим следующее уравнение:

\begin x'(t_0)\cdot(X-x(t_0))+y'(t_0)\cdot(Y-y(t_0))+z'(t_0)\cdot(Z-z(t_0))=0. \end

Соприкасающаяся плоскость

Плоскость, проходящую через заданную точку $M$ кривой $\gamma$ параллельно векторам $\vec(t_0)$, $\vec(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.

Если $\vec$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $\vec-\vec(t_0)$, $\vec(t_0)$, $\vec(t_0)$:

Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:

\begin \left| \begin X-x(t_0) & Y-y(t_0) & Z-z(t_0) \\ x'(t_0) & y'(t_0) & z'(t_0)\\ x»(t_0) & y»(t_0) & z»(t_0) \\ \end \right|=0 \end

Бинормаль и главная нормаль

Прямая, проходящая через точку $M$ кривой $\gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.

Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.

Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.

Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.

Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ \vec(t_0)\times\vec(t_0)$, тогда ее уравнение можно записать в виде:

Как и раньше, $\vec$ — радиус-вектор произвольной точки бинормали. Каноническое уравнение прямой:

Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $\vec(t_0) \times\left[\vec(t_0),\vec(t_0)\right]$:

Уравнение в каноническом виде распишите самостоятельно.

Спрямляющая плоскость

Плоскость, проходящую через заданную точку $M$ кривой $\gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.

Другое определение: Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.

Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $\vec-\vec(t_0)$, $\vec(t_0)$, $\vec(t_0)\times\vec(t_0)$: \begin \left(\vec-\vec(t_0),\, \vec(t_0),\, \vec(t_0)\times\vec(t_0)\right)=0. \end Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.

Репер Френе

Орт (то есть единичный вектор) касательной обозначим: $$ \vec<\tau>=\frac<\vec(t_0)><|\vec(t_0)|>. $$ Орт бинормали: $$ \vec<\beta>=\frac<\vec(t_0)\times\vec(t_0)><|\vec(t_0)\times\vec(t_0)|>. $$ Орт главной нормали: $$ \vec<\nu>=\frac<\vec(t_0) \times[\vec(t_0),\,\vec(t_0)]><|\vec(t_0) \times [\vec(t_0),\,\vec(t_0)]|>. $$

Правая тройка векторов $\vec<\tau>$, $\vec<\nu>$, $\vec<\beta>$ называется репером Френе.

Решение задач

Задача 1

Кривая $\gamma$ задана параметрически:

Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$. Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.

Решение задачи 1

Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.

Начнем с производных.

\begin 1\cdot X+0\cdot Y+1\cdot (Z-1)=0\,\,\ \Rightarrow \,\, X+Z=1. \end

\begin \left| \begin X-0 & Y-0 & Z-1 \\ 1 & 0 & 1\\ 0 & 2 & 1 \\ \end \right|=0 \end Раскрываем определитель, получаем уравнение: \begin -2X-Y+2Z-2=0 \end

\begin 1\cdot X-4\cdot Y-1\cdot (Z-1)=0\,\,\ \Rightarrow \,\, X-4Y-Z+1=0. \end

Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $\vec<\tau>$, $\vec<\nu>$, $\vec<\beta>$ не будет правой (по определению векторного произведения вектор $\vec<\tau>\times\vec<\beta>$ направлен так, что тройка векторов $\vec<\tau>$, $\vec<\beta>$, $\vec<\nu>=\vec<\tau>\times\vec<\beta>$

— правая). Изменим направление одного из векторов. Например, пусть

Теперь тройка $\vec<\tau>$, $\vec<\nu>$, $\vec<\tilde<\beta>>$ образует репер Френе для кривой $\gamma$ в точке $M$.

Задача 2

Написать уравнение соприкасающейся плоскости к кривой $$ x=t,\,\, y=\frac<2>,\,\, z=\frac<3>, $$ проходящей через точку $N(0,0,9)$.

Решение задачи 2

Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $\gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)\in\gamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.

Найдем значение параметра $t_0$.

Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.

Соприкасающаяся плоскость определяется векторами $\vec(t_0)$, $\vec(t_0)$, поэтому записываем определитель \begin \left| \begin X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \\ &&\\ 1 & t_0 & t^2_0 \\ &&\\ 0 & 1 & 2t_0 \end \right|=0 \quad \Rightarrow \end

\begin (X-t_0)\cdot t_0^2 — (Y-t_0^2/2)\cdot 2t_0 + (Z-t_0^3/3)=0. \end Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$: \begin 9-t_0^3/3=0 \quad \Rightarrow \quad t_0=3. \end Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости: $$ 9X-6Y+Z-9=0. $$

Задача 3

Через точку $P\left(-\frac45,1,2\right)$ провести плоскость, являющуюся спрямляющей для кривой: $$ x=t^2,\,\, y=1+t,\,\, z=2t. $$

Решение задачи 3

Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.

Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $\vec(t_0)$ и $\vec(t_0)\times\vec(t_0)$.

Записываем уравнение спрямляющей плоскости: \begin \left| \begin X-t_0^2 & Y-1-t_0 & Z-2t_0 \\ 2t_0 & 1 & 2\\ 0 & 4 & -2 \end \right|= 0 \end

Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$: \begin 5t_0^2-8t_0-4=0 \,\, \Rightarrow \,\, t_<01>=2,\, t_<02>=-\frac25. \end

Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид: \begin & 5X-4Y-8Z+24=0,\\ & 25X+4Y+8Z=0. \end

Нормальное уравнение плоскости: описание, примеры, решение задач

Статья раскрывает суть нормального (нормированного) уравнения и показывает, при каких видах задач его чаще всего применяют. Рассмотрим выведение нормального уравнения плоскости с примерами решений. Приведем примеры приведения общего уравнения плоскости к нормальному виду. Решим задачи по нахождению расстояния от точки до плоскости при помощи нормального уравнения плоскости.

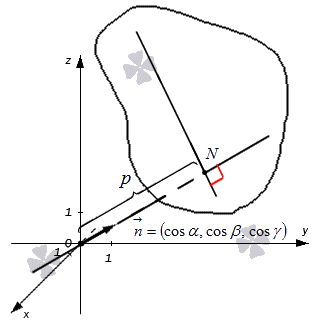
Нормальное уравнение плоскости – описание и пример

Возьмем прямоугольную систему координат О х у z трехмерного пространства. Если плоскость удалена на расстояние p ≥ 0 в положительном направлении нормального вектора n → . Возьмем за единицу длину вектора n → . Получим, что координатами направляющего косинуса являются n → = ( cos α , cos β , cos γ ) , тогда n → = cos 2 α , cos 2 β , cos 2 γ = 1 .

Примем обозначение O N за расстояние от точки до плоскости, таким образом, точка N принадлежит плоскости, где длиной отрезка O N будет значение p . Представим это на рисунке, изображенном ниже.

Теперь найдем уравнение заданной плоскости.

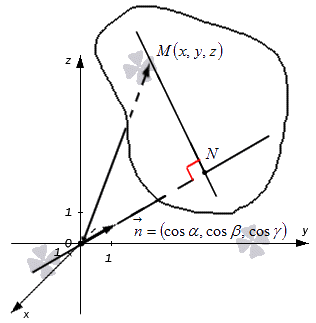
В трехмерном пространстве обозначим точку M ( x , y , z ) . Отсюда получим, что O M → , являющийся ее радиус вектором, с координатами ( x , y , z ) . Запись примет вид O M → = ( x , y , z ) . Отсюда получаем, что плоскость определена множеством точек M ( x , y , z ) , тогда числовая проекция вектора O M → по направлению n → равна значению p . Запись принимает вид n p n → O M → = p . Рассмотрим на приведенном ниже рисунке.

Из вышесказанного получим, что определение скалярного произведения векторов по формуле n → = ( cos α , cos β , cos γ ) и O M → = ( x , y , z ) в результате дают равенство

n → , O M → = n → · O M → · cos n ⇀ , O M → ^ = n → · n p n → O M → = 1 · p = p

Данная формула представляет скалярное произведение в координатной форме. Тогда получаем следующее выражение:

n → , O M → = cos α · x + cos β · y + cos γ · z

При сопоставлении двух последних равенств получаем уравнение плоскости такого вида cos α · x + cos β · y + cos γ · z = p . Упростим выражения. Для этого необходимо перенести значение p в левую сторону, получим cos α · x + cos β · y + cos γ · z — p = 0 .

cos α · x + cos β · y + cos γ · z — p = 0 называют нормальным уравнением плоскости или уравнением плоскости в нормальном виде. Реже его называют нормированным уравнением заданной плоскости.

Теперь заданное в прямоугольной системе координат О х у z нормальное уравнение принимает вид cos α · x + cos β · y + cos γ · z — p = 0 . Р имеет значение расстояния положительного направления единичного нормального вектора плоскости n → = ( cos α , cos β , cos γ ) .

Чаще всего косинус не представляется явно в уравнении плоскости, потому как cos α , cos β и cos γ является некоторыми действительными числами, сумма квадратов которых равна единице.

Рассмотрим пример нормального уравнения плоскости.

Если имеется плоскость, заданная в прямоугольной системе координат O x y z при помощи уравнения нормального вида, — 1 4 · x — 3 4 · y + 6 4 · z — 7 = 0 .

Отсюда cos α = — 1 4 , cos β = — 3 4 , cos γ = 6 4 .

Из выражения находим, что — 1 4 , — 3 4 , 6 4 — координаты нормального вектора плоскости n → . Его длина вычисляется из формулы n → = — 1 4 2 + — 3 4 2 + 6 4 2 = 1 . Плоскость располагается относительно координат в направлении вектора n → на расстоянии 7 единиц, потому как p = 7 .

Отсюда ясно, что нормальное уравнение плоскости представляет собой общее уравнение плоскости A x + B y + C z + D = 0 , где A , B , C – некоторые действительные числа, при которых длина нормального вектора плоскости n → = ( A , B , C ) равняется 1 , причем D является неотрицательным числом.

Чтобы выявить, является представленное уравнение нормальным уравнением плоскости, необходимо выполнение обоих условий n → = cos 2 α + cos 2 β + cos 2 γ = 1 и p ≥ 0 , тогда получим уравнение плоскости нормального вида. При невыполнении хотя бы одного условия, уравнение не является нормальным.

Рассмотрим на примере.

Выявить уравнение плоскости нормального вида из заданных уравнений:

1 7 x — 4 7 y + 4 2 7 — 3 = 0 1 3 x + 7 6 y — 5 6 z + 2 5 = 0 1 3 x + 1 2 y + 1 4 z — 11 = 0

Начнем решение с первого уравнения. Для этого необходимо проверить, равняется ли длина нормального вектора n → = 1 7 , — 4 7 , 4 2 7 единице.

Вычисляем длину по формуле и получаем: n → = 1 7 2 + — 4 7 2 + 4 2 7 2 = 1 49 + 16 49 + 32 49 = 1

Необходимо поработать с числом p , так как его значение должно быть положительным. Это верно, так как p = 3 . Значит, первое заданное уравнение плоскости можно считать уравнением плоскости в нормальном виде.

Второе уравнение из заданных нельзя считать нормальным уравнением плоскости, так как условие p ≥ 0 не выполняется, ибо в данном уравнении p = — 2 5 .

Третье уравнение имеет нормальный вектор с координатами n → = 1 3 , 1 2 , 1 4 , длина которого не равняется единице из вычислений:

n → = 1 3 2 + 1 2 2 + 1 4 2 = 1 9 + 1 4 + 1 16 = 61 12 ≠ 1

Отсюда следует, что его нельзя считать за уравнение плоскости в нормальном виде.

Ответ: 1 7 x — 4 7 y + 4 2 7 z — 3 = 0 уравнение является нормальным уравнением плоскости.

Приведение общего уравнения плоскости к нормальному виду

Для приведения уравнения плоскости A x + B y + C z + D = 0 к нормальному виду, обе части умножаются на нормированный множитель ± 1 A 2 + B 2 + C 2 . Знак определятся по числу D , он должен быть противоположным значения числа D .

Когда D = 0 , знак может быть любым.

Нормальным уравнением плоскости считается общее уравнение плоскости после умножения на нормирующий множитель, потому как длина вектора с кооординатами ± A A 2 + B 2 + C 2 , ± B A 2 + B 2 + C 2 , ± C A 2 + B 2 + C 2 равна 1 .

Отсюда получаем, что ± A A 2 + B 2 + C 2 , ± B A 2 + B 2 + C 2 , ± C A 2 + B 2 + C 2 = A 2 + B 2 + C 2 A 2 + B 2 + C 2 = 1 .

Знак множителя необходим для того, что проверять выполнимость условия p ≥ 0 .

Привести уравнение 2 x — 3 y + z + 5 = 0 к нормальному виду.

Из условия имеем, что A = 2 , B = — 3 , C = 1 , D = 5 . Исходя из того, что D является положительным числом, нормирующий множитель дожжен иметь противоположный знак. Отсюда получим, что получим отрицательный результат.

— 1 A 2 + B 2 + C 2 = — 1 2 2 + ( — 3 ) 2 + 1 2 = — 1 14

Чтобы получить искомое нормальное уравнение плоскости, обе части уравнения необходимо умножить на нормирующий множитель. Получим:

— 1 14 · 2 x — 3 y + z + 5 = — 1 14 · 0 ⇔ ⇔ — 2 14 x + 3 14 y — 1 14 z — 5 14 = 0

Ответ: — 2 14 x + 3 14 y — 1 14 z — 5 14 = 0 .

Написать нормальное уравнение плоскости, если оно задано уравнением 3 x — 4 z = 0 прямоугольной системы координат O x y z .

Из условия видно, что A = 3 , B = 0 , C = — 4 , D = 0 . Знака перед множителем нет, потому как D = 0 . Значит, возьмем со знаком « + ». Получаем выражение вида:

1 A 2 + B 2 + C 2 = 1 3 2 + 0 2 + ( — 4 ) 2 = 1 5

При умножении обеих частей уравнения на нормирующий множитель, получаем уравнение плоскости нормального вида 3 5 x — 4 5 z = 0 .

Ответ: 3 5 x — 4 5 z = 0 .

Нахождение расстояния от точки до плоскости

Теперь раскроем тему нормального уравнения плоскости, где уравнение плоскости нормального вида применимо для нахождения расстояния от заданной точки в пространстве до плоскости.

При заданной системе координат О х у z трехмерного пространства имеем плоскость с уравнением cos α · x + cos β · y + cos γ · z — p = 0 , где необходимо определить расстояние от p до точки M 0 ( x 0 , y 0 , z 0 ) заданной плоскости. Его вычисляют по формуле p = cos α · x 0 + cos β · y 0 + cos γ · z 0 — p . Само расстояние является числом, которое получается при подстановке координат точки в левую сторону уравнения. Для вывода формулы необходимо обратиться к статье расстояния от точки до плоскости.

Имеется уравнение плоскости вида — 1 3 x + 2 3 y — 2 3 z — 1 = 0 , которое располагается в прямоугольной системе координат. Определить расстояние от точки с координатами M 0 ( 1 , — 3 , 0 ) до плоскости.

Координаты точки M необходимо подставить в левую часть уравнения плоскости. Тогда получаем:

— 1 3 · 1 + 2 3 · ( — 3 ) — 2 3 · 0 — 1 = 0

Искомое расстояние – величина абсолютная, значит p = — 3 1 3 = 3 1 3 .

Если плоскость задана другим уравнением, а необходимо произвести вычисление от заданной точки до плоскости, необходимо привести уравнение к виду нормального уравнения плоскости, используя формулу p = cos α · x 0 + cos β · y 0 + cos γ · z 0 — p .

Найти расстояние от заданной точки с координатами M 0 ( 5 , — 1 , 2 ) до плоскости x 5 + y — 2 + z 4 = 1 .

По условию имеем уравнение плоскости в отрезках. Это значит, что необходимо привести его к нормальному уравнению плоскости. Для этого переходим к общему уравнению, после чего приведем к нормальному виду.

Получаем: x 5 + y — 2 + z 4 = 1 ⇔ 1 5 x — 1 2 y + 1 4 z — 1 = 0

Для вычисления нормирующего множителя применяем: 1 1 5 2 + — 1 2 2 + 1 4 2 = 1 141 25 · 16 = 20 141

Обе части уравнения 1 5 x — 1 2 y + 1 4 z — 1 = 0 умножаем на нормирующий множитель. Теперь получено нормальное уравнение исходной плоскости вида:

4 141 x — 10 141 y + 5 141 z — 20 141 = 0

Отсюда видно, что cos α = 4 141 , cos β = — 10 141 , cos γ = 5 141 , p = — 20 141 , x 0 = 5 , y 0 = — 1 , z 0 = 2

Все имеющиеся данные помогут использовать формулу для нахождения искомого расстояния от точки до плоскости:

p = cos α · x 0 + cos β · y 0 + cos γ · z 0 — p = 4 141 · 5 — 10 141 · — 1 + 5 141 · 2 — 20 141 = 20 141

Нормальная плоскость и главная нормаль кривой

Нормальная плоскость.

Плоскость \(\mathcal

\), проходящую через точку \(M_<0>\) кривой \(\Gamma\) и перпендикулярную касательной к этой кривой в точке \(M_<0>\), называют нормальной плоскостью кривой \(\Gamma\) в точке \(M_<0>\).

Рис. 22.5

Если кривая \(\Gamma\) задана уравнением в векторной форме
$$
\Gamma=<\textbf=\textbf(t),\ \alpha\leq t\leq\beta>,\label
$$
где
$$
\textbf=(x,y,z),\quad \textbf(t)=(x(t),y(t),z(t)),\nonumber
$$
\(t_<0>\in[\alpha,\beta]\), \(\overrightarrow=\textbf(t_0)\) и \(\textbf‘(t_0)\neq 0\), то вектор \(\textbf‘(t_0)\) параллелен касательной к кривой \(\Gamma\) в точке \(M_<0>\). Пусть \(M\) — произвольная точка нормальной плоскости \(\mathcal

\) (рис. 22.5), \(\overrightarrow=\textbf\). Тогда вектор \(\overrightarrow_<0>=\textbf-\textbf(t_0)\) перпендикулярен вектору \(\textbf‘(t_<0>)\), и поэтому уравнение нормальной плоскости \(\mathcal

\) к кривой \(\Gamma\) в точке \(M_<0>\) можно записать в виде
$$
(\textbf-\textbf(t_<0>),\textbf‘(t_<0>))=0\nonumber
$$
или
$$
(x-x(t_<0>))x'(t_0)+(y-y(t_<0>))y'(t_<0>)+(z-z(t_0))z'(t_0)=0.\nonumber
$$

Главная нормаль.

Любую прямую, лежащую в нормальной плоскости \(\mathcal

\) к кривой \(\Gamma\) в точке \(M_<0>\), называют нормалью кривой \(\Gamma\) в точке \(M_<0>\). Среди всех нормалей выделяют одну — главную нормаль.

Понятие главной нормали требует введения дополнительных ограничений на вектор-функции, с помощью которых записываются уравнения кривых. Пусть \(\Gamma\) — гладкая кривая, заданная уравнением \eqref, причем для всех \(t\in[\alpha,\beta]\) существует \(\textbf″(t)\). В этом случае говорят, \(\Gamma\) — дважды дифференцируемая кривая без особых точек.

Если \(\Gamma\) — дважды дифференцируемая кривая без особых точек, заданная уравнением \eqref, \(s\) — переменная длина дуги кривой \(\Gamma\), то существуют \(\displaystyle \frac>\) и \(\displaystyle \frac\textbf>>\) и справедливы равенства
$$
\frac>=\frac<\textbf‘(t)>,\label
$$
$$
\fracr\textbf<>>>=\frac″(t)-s″(t)\textbf‘(t)><(s(t))^<3>>.\label
$$

\(\circ\) Применяя правило дифференцирования вектор-функции при замене переменного, получаем формулу \eqref:
$$
\frac>=\frac>