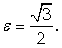Для кривой уравнение диаметра проходящего через точку

Для кривой уравнение диаметра проходящего через точку

Глава 22. Диаметры линий второго порядка

В курсе аналитической геометрии доказывается, что середины параллельных хорд линии второго порядка лежат на одной прямой. Эта прямая называется диаметром линии второго порядка. Диаметр, делящий пополам какую-нибудь хорду (а значит, и все параллельные ей), называется сопряженным этой хорде (и всем хордам, который ей параллельны). Все диаметры эллипса и гиперболы проходят через центр. Если эллипс задан уравнением

(1)

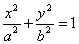
то его диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

.

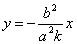
Если гипербола задана уравнением

, (2)

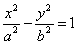
то ее диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

.

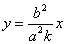
Все диаметры параболы параллельны ее оси. Если парабола задана уравнением

,

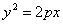
то ее диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

.

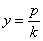
Если один из двух диаметров эллипса или гиперболы делит пополам хорды, параллельные другому, то второй диаметр делит пополам хорды, параллельные первому. Такие два диаметра называются взаимно сопряженными.

Если k и k ’ — угловые коэффициенты двух взаимно сопряженных диаметров эллипса (1), то

(3)

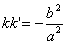
Если k и k ’ — угловые коэффициенты дух взаимно сопряженных диаметров гиперболы (2), то

(4).

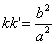
Соотношения (3) и (4) называются условиями сопряженности диаметров соответственно для эллипса и для гиперболы.

Диаметр линии второго порядка, перпендикулярный к сопряженным хордам, называется главным.

Уравнение кривой второго порядка

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Диаметры кривой. Главные оси. Асимптоты. Уравнение кривой, отнесенной к сопряженным направлениям; уравнение кривой, отнесенной к асимптотам.

Если в кривой второго порядка провести все хорды одного и того же направления, то геометрическое место середин этих хорд представит некоторую прямую, которую называют диаметром, сопряженным данным хордам. Уравнение диаметра:

где есть угловой коэффициент сопряженных хорд. Меняя , т.е. меняя направление хорд, получим бесчисленное множество диаметров; все они проходят через центр кривой. У параболы все диаметры параллельны между собой.

Направление хорд и направление сопряженного им диаметра называются сопряженными направлениями относительно данной кривой. Зависимость между двумя сопряженными направлениями следующая:

Сопряженными диаметрами называются такие два диаметра, из которых каждый делит пополам хорды, параллельные другому. У параболы сопряженных диаметров нет, так как все диаметры имеют одно и тоже направление.

Главными осями кривой называются диаметры, перпендикулярные к сопряженным хордам; их направления называются главными направлениями.

В случае прямоугольной системы координат главные направления определяются из уравнения:

где – угол между одним из главных направлений и направлением оси .

В случае косоугольной системы координат имеем:

Всякая кривая второго порядка имеет два главных направления, за исключением окружности, для которой главные направления неопределенные.

Угловой коэффициент определяется для всех диаметров параболы по формуле:

если для старших коэффициентов параболы введены обозначения:

Главная ось параболы как один из ее диаметров имеет это же направление и в случае прямоугольных координат она изображается уравнением

Второе главное направление параболы перпендикулярно к ее диаметрам, но второй главной оси у параболы нет. Если отнести кривую у двум сопряженным направлениям, т.е. выбрать за оси координат прямые, имеющие сопряженные направления относительно этой кривой, то в уравнение кривой не войдет член с произведением координат (). У параболы кроме того, исчезнет ещё один из старших членов ().

Если центральную кривую отнести к двум сопряженным диаметрам (или к главным осям), то уравнение ее примет вид:

Простейшее уравнение параболы мы получим, поместив начало координат в вершину, т.е. в точку пересечения параболы с главной осью (), выбрав главную ось за ось абсцисс (, и ) и касательную в вершине (она перпендикулярна к оси) за ось ординат:

При таком же выборе осей координат центральная кривая изобразится уравнением

Асимптоты кривой можно рассматривать как те ее диаметры, которые сами себе сопряжены. Угловые коэффициенты асимптот определяются из уравнения

Асимптоты могут быть только у центральных кривых: гипербола имеет две действительные асимптоты, эллипс – две мнимые; в случае пересекающихся прямых асимптоты совпадают с этими прямыми.

Если принять асимптоты гиперболы за оси координат, то уравнение этой гиперболы примет вид:

587. Найти два сопряженных диаметра кривой , из которых один проходит через начало координат.

Решение . Данная кривая центральная, потому что . Уравнение всякого ее диаметра будет где — угловой коэффициент сопряженного диаметра. Так как искомый диаметр проходит через начало координат, то свободный член его уравнения должен равняться нулю, т.е. откуда . Вставив это значение параметра в общее уравнение диаметра и преобразовав его, получим: . Это уравнение одного из искомых диаметров; его угловой коэффициент ; следовательно, уравнение сопряженного диаметра будет:

588. Через точку (1;-2) проведен диаметр кривой . Найти уравнение этого диаметра и диаметра ему сопряженного.

589. Дана кривая . Найти ее диаметр, параллельный оси абсцисс, и диаметр, ему сопряженный.

590. Найти два сопряженных диаметра кривой , из которых один параллелен оси ординат.

591. Дана кривая и один из ее диаметров . Найти диаметр, ему сопряженный.

592. Составить уравнение диаметра кривой , параллельного прямой .

593. Определить диаметр кривой , образующий угол в с осью абсцисс. Угол .

594. Дана кривая: . Найти геометрическое место середин ее хорд: 1) параллельных оси ; 2) параллельных оси ; 3) параллельных прямой .

595. Найти диаметр кривой , проходжящей через середину хорды, отсекаемой этой кривой на прямой .

596. Найти середину хорды, отсекаемой кривой на прямой .

597. Найти такие сопряженные диаметры кривой , которые образуют между собой угол в . Угол .

598. Найти зависимость между угловыми коэффициентами прямых, имеющих сопряженные направления относительно:

1) эллипса ; 2) гиперболы .

599. Через точку (1;-3) провести хорду эллипса , сопряженную диаметру .

600. Найти направления и длину двух сопряженных диаметров эллипса , из которых один проходит через точку (2;3).

601. Найти угол между двумя сопряженными диаметрами эллипса , из которых один образует угол в с большой осью.

602. Определить длину тех сопряженных диаметров эллипса , которые образуют между собой угол .

Указание . В этой задаче удобно воспользоваться теоремами Аполлония: и , где и – полуоси эллипса; и — сопряженные полудиаметры его; – угол между этими сопряженными диаметрами.

603. Даны размеры двух сопряженных диаметров эллипса и и угол между ними . Вычислить длину его осей.

604. Определить угол между двумя сопряженными диаметрами гиперболы , зная, что действительный из этих диаметров втрое больше действительной оси.

605. Найти уравнения двух сопряженных диаметров гиперболы , угол между которыми равняется .

606. Дана парабола: . Написать уравнение диаметра этой параболы:

1) проходящего через начало координат;

2) сопряженного хордам, параллельным оси ;

3) сопряженного хордам, параллельным оси ;

4) образующего угол с сопряженными хордами;

5) перпендикулярного к сопряженным хордам.

Во всех случаях угол

607. Найти диаметр параболы , сопряженный тем хордам, которые наклонены под углом в к оси параболы.

608. Написать уравнение диаметра параболы , сопряженного с прямой .

609. Найти главные оси кривых:

Во всех случаях угол

610. Каковы будут главные оси распавшейся центральной кривой?

611. Найти ось параболы .

Решение . Все диаметры данной параболы имеют угловой коэффициент . Ось параболы есть диаметр, сопряженный перпендикулярным хордам, т.е. хордам с угловым коэффициентом (система координат предполагается прямоугольной). Уравнение всякого диаметра этой параболы будет при мы получим уравнение оси: .

612. Найти ось симметрии и вершину каждой из следующих парабол:

Во всех случаях угол

Указание . Вершина параболы находится как точка пересечение параболы с ее осью.

613. Найти общий диаметр двух кривых:

614. Составить уравнение кривой второго порядка, проходящей через начало координат, если известны две пары сопряженных ее диаметров:

Решение . Угловые коэффициенты сопряженных диаметров удовлетворяют уравнению: . Угловые коэффициенты данных диаметров: и , , ; вставляя эти значения в указанное уравнение, получим:

Координаты центра искомой кривой мы можем определить, решая совместно уравнения двух диаметров: , . Эти координаты должны удовлетворять уравнениям: и которые данном случае перепишутся так: и ; вставим вместо : и вычисленные их значения и тогда получим: и . Кроме того, кривая проходит через начало координат; значит, , и уравнение кривой будет:

615. Две пары прямых:

служат сопряженными диаметрами кривой второго порядка. Составить уравнение этой кривой, зная, что она проходит через точку (1;1).

616. Выяснить особенности в выборе осей координат, если кривые даны следующими уравнениями:

617. Относительно некоторой прямоугольной системы координат кривая дана уравнением: . Преобразовать это уравнение, приняв за оси координат главные оси кривой.

618. Отнести к главным осям кривые, данные относительно прямоугольной системы координат уравнениями:

619. Уравнение кривой, отнесенной к двум сопряженным диаметрам, составляющим угол , имеет вид: . Найти уравнение той же кривой относительно ее главных осей.

620. Отнести к главным осям кривые:

621. Выяснить особенности в выборе осей координат, если параболы даны следующими уравнениями:

622. привести к простейшему виду уравнение параболы ; .

623. Привести к простейшему виду уравнения следующих парабол:

624. Отнести к вершине следующие центральные кривые:

Во всех случаях .

625. Найти асимптоты следующих гипербол:

626. Доказать, что все кривые, уравнения которых отличаются друг от друга только свободными членами, имеют общие асимптоты. Найти, например, асимптоты кривых при различных значениях параметра λ.

627. Доказать, что если две кривые имеют общие асимптоты, то все члены их уравнений, кроме свободных членов, имеют пропорциональные коэффициенты.

628. Составить общее уравнение для всех кривых. Имеющих прямые и своими асимптотами.

629. кривая второго порядка проходит через точку (1;-1) и имеет своими асимптотами две прямые: и . Составить уравнение этой кривой.

630. Составить уравнение кривой, касающейся прямой и имеющей прямые и своими асимптотами.

630*. Какому условию удовлетворяют коэффициенты общего уравнения гиперболы, если гипербола равносторонняя?

631. Какой вид имеет уравнение гиперболы, если одна из осей координат или обе оси параллельны асимптотам?

632. Составить уравнение гиперболы, проходящей через точки (2;1), (-1;-2) и (), при условии, что одна из ее асимптот совпадает с осью абсцисс.

633. Уравнение гиперболы, отнесенной к главным осям, имеет вид: . Преобразовать это уравнение, приняв асимптоты гиперболы за новые оси координат.

634. Отнести гиперболу к ее асимптотам.

635. Как преобразуется уравнение гиперболы , если за оси координат принять ее асимптоты? Угол .

636. Сколько членов второй степени и какие именно могут войти в уравнение: 1) эллипса4 2) гиперболы; 3) параболы?

Преобразование уравнения кривой второго порядка с помощью инвариантов.

Если одна и та же кривая второго порядка, отнесенная к двум различным произвольно выбранным системам координат с координатными углами и , изображается уравнениями:

то имеют место следующие равенства:

т.е. существуют выражения, составленные из коэффициентов уравнения кривой и соответствующего координатного угла, которые не меняют своей величины ни при каком преобразовании декартовых координат. Такие выражения называются инвариантами кривой второго порядка. Мы можем пользоваться тремя вышеприведенными инвариантами:

для упрощения уравнений кривой второго порядка, если только уравнение кривой после преобразования содержит не более трех коэффициентов.

637. Пользуясь инвариантами, отнести к главным осям кривую , зная что .

Решение . Искомое уравнение имеет следующий вид:

Для прямоугольных систем координат инварианты упрощаются, так как и , и мы будем иметь: ; . Найдем числовое значение этих инвариантов, исходя из данного уравнения:

Составим теперь выражения этих же инвариантов через коэффициенты преобразованного уравнения: . Так как инварианты не меняют своей величины при преобразовании координат, то мы можем приравнять между собой найденные для них выражения, содержащие коэффициенты первоначального и преобразованного уравнения;. Из этой системы уравнений мы определяем неизвестные коэффициенты преобразованного уравнения: ;, и искомое уравнение будет . Таким образом, пользуясь инвариантами, можно привести уравнение кривой к простейшему виду, не отыскивая ее центра, осей и не составляя формул преобразования координат.

638. Пользуясь инвариантами, привести к простейшему виду уравнения следующих кривых:

при условии, что все они отнесены к прямоугольной системе координат.

639. Пользуясь инвариантами, упростить уравнения следующих кривых:

Во всех случаях .

640. Упростить уравнения следующих кривых:

640*. Отнести к главным осям кривую , если известно, что .

641. Отнести гиперболу к ее асимптотам, пользуясь инвариантами. Угол .

Решение . Уравнение кривой, отнесенной к асимптотам, имеет вид:

Нам надо найти два неизвестных коэффициента , и новый координатный угол , т.е. угол между асимптотами. Найдем числовую величину инвариантов, пользуясь данным уравнением, при , : . Выражения этих инвариантов в новых коэффициентах будут:

Для определения трех величин , и имеем три уравнения:

Решив их, получим: , ; и ; искомое уравнение будет: . Выбираем направление осей так, чтобы гипербола была расположена в нормальном угле и вертикальном к нему угле; тогда после упрощений получим: .

642. Отнести к асимптотам гиперболы, данные относительно прямоугольной системы координат уравнениями:

643. Относительно некоторой прямоугольной системы координат кривая изображается уравнением . Составить уравнение этой же кривой относительно ее вершины.

Указание . Отнести кривую к вершине – значит принять одну из осей кривой за ось абсцисс, перенести начало координат в вершину и принять касательную в вершине за ось ординат.

5.2.8. Примеры решения задач по теме «Кривые 2-го порядка»

Определить тип уравнения кривой 2-го порядка:

Если L1·L2 > 0, то уравнение эллиптического типа;

Если L1·L2 0, следовательно, перед нами уравнение эллиптического типа.

В уравнении отсутствует произведение Ху, следовательно, квадратичная форма его старших членов имеет канонический вид; поэтому коэффициенты при Х2 и У2 являются собственными числами матрицы квадратичной формы. Итак, L1 = 4, L2 = 9, L1·L2 > 0, следовательно, перед нами уравнение эллиптического типа.

Геометрические образы, определяемые уравнением эллиптического типа:

— пустое множество («мнимый эллипс»).

Для приведения уравнения к каноническому виду нужно исключить из него слагаемые. Содержащие первые степени переменных. Для этого преобразуем левую часть:

Зададим параллельный перенос осей координат:

Тогда в новых координатах уравнение примет вид:

Каноническое уравнение эллипса.

Ответ: уравнение эллипса, канонический вид .

Привести уравнение к каноническому виду и указать геометрический образ, который оно определяет:

Собственные числа имеют разные знаки, значит, тип уравнения – гиперболический.

Геометрические образы, определяемые уравнением гиперболического типа:

— пара пересекающихся прямых.

Собственные числа имеют разные знаки, значит, тип уравнения – гиперболический.

Геометрические образы, определяемые уравнением гиперболического типа:

— пара пересекающихся прямых.

Заметим, что для данного уравнения нет необходимости искать явный вид преобразования координат, приводящего квадратичную форму к каноническому виду. Это связано с тем, что уравнение не содержит линейных членов, а его свободный член не изменится при преобразовании вида

Найденные собственные числа будут коэффициентами при Х2 и У2 для канонического вида квадратичной формы. Следовательно, в соответствующей координатной системе уравнение примет вид:

Каноническое уравнение гиперболы.

Ответ: уравнение гиперболического типа, канонический вид

.

Привести уравнение к каноническому виду и указать геометрический образ, который оно определяет:

Перед нами полное уравнение 2-го порядка, и для приведения его к каноническому виду потребуется провести оба преобразования координатных осей: поворот на такой угол, чтобы новые оси стали параллельными собственным векторам матрицы квадратичной формы (это преобразование квадратичной формы к каноническому виду), и параллельный перенос.

Перед нами полное уравнение 2-го порядка, и для приведения его к каноническому виду потребуется провести оба преобразования координатных осей: поворот на такой угол, чтобы новые оси стали параллельными собственным векторам матрицы квадратичной формы (это преобразование квадратичной формы к каноническому виду), и параллельный перенос.

Итак, тип уравнения – гиперболический.

Матрица перехода к новому базису:

.

Собственные векторы следует выбирать так, чтобы определитель матрицы перехода равнялся +1 – при этом не нарушается взаимное расположение координатных осей.

Запишем исходное уравнение в новых координатах:

2) Параллельный перенос:

В новых координатах получаем уравнение

Пара пересекающихся прямых.

Ответ: уравнение гиперболического типа, определяет пару пересекающихся прямых, канонический вид: У″ = ± 2Х″.

Не проводя преобразования координат, установить, что уравнение

Определяет прямую, и найти уравнение этой прямой.

Обратите внимание на то, что квадратичная форма, образованная старшими членами уравнения, является полным квадратом.

Иногда привести уравнение к простому виду удается с помощью алгебраических приемов. Представим левую часть уравнения в виде:

Ответ: уравнение определяет прямую Х – 3У + 2 = 0.

Эллипс, симметричный относительно осей координат, проходит через точки

Найти его эксцентриситет.

По условию задачи оси координат являются осями симметрии эллипса, поэтому, во-первых, его уравнение имеет канонический вид, а во-вторых, полуось А равна абсциссе точки А.

По условию задачи оси координат являются осями симметрии эллипса, поэтому, во-первых, его уравнение имеет канонический вид:

А во-вторых, полуось А равна абсциссе точки А, т. е. А = 6. Найдем B, подставив в уравнение эллипса координаты точки М:

Итак, уравнение эллипса:

Тогда расстояние от фокуса до начала координат

Вычислим эксцентриситет эллипса:

Ответ: эксцентриситет

Составить уравнение эллипса, фокусы которого лежат на прямой У + 6 = 0, эксцентриситет равен , а точка М(3; -1) является концом малой полуоси.

Найдите расстояние от точки М до прямой У + 6 = 0, т. е. длину малой полуоси эллипса. Центром симметрии эллипса будет точка О пересечения прямых F1F2 (Y + 6 = 0) и МО, проходящей через точку М перпендикулярно F1F2.

Найдем расстояние от точки М до прямой У + 6 = 0, т. е. длину малой полуоси эллипса. Нормальный вид уравнения данной прямой: -у – 6 = 0, тогда

Центром симметрии эллипса будет точка О пересечения прямых F1F2 (Y + 6 = 0) и МО, проходящей через точку М перпендикулярно F1F2.

Поскольку прямая F1F2 параллельна оси абсцисс, прямая МО параллельна оси ординат; следовательно, ее уравнение: Х = 3. Тогда координаты точки О:

С учетом расположения осей эллипса можно утверждать, что в системе координат, полученной параллельным переносом начала координат в точку

О(3; -6), то есть заданной преобразованием

Уравнение эллипса имеет канонический вид:

Найдем А из условия, что

Подставим найденные значения А и B в уравнение эллипса:

Ответ: уравнение эллипса: Х2 + 2У2 – 6Х + 24У + 31 = 0.

Составить уравнения директрис гиперболы.

Приведите уравнение гиперболы к каноническому виду и составьте уравнения директрис в виде

Приведем уравнение гиперболы к каноническому виду:

Осями симметрии являются координатные оси, А = 3, B = 4. Тогда

Ответ: уравнения директрис:

Написать уравнение гиперболы, имеющей вершины в фокусах, а фокусы – в вершинах эллипса

Найдите вначале координаты вершин и фокусов эллипса, а затем определите коэффициенты А и B в каноническом уравнении гиперболы.

Координаты вершин гиперболы: (А; 0) и (-А; 0), координаты фокусов: (С; 0) и (–С; 0). Соответственно координаты вершин эллипса: (А1; 0) и (-А1; 0), координаты фокусов: (С1; 0) и (-С1; 0). У данного эллипса А1 = 5,

Тогда для гиперболы А = 4, С = 5, откуда

,

И уравнение гиперболы:

Ответ:

Составить уравнение касательной к гиперболе

В ее точке М=<15; 4>.

Найдите вначале координаты нормали к гиперболе в точке М (если кривая задана уравнением F(X,Y) = 0, То нормаль к ней в точке М0=<Х0;у0>

Имеет координаты: П = (F′X(X0;Y0);F′Y(X0;Y0))), а затем составьте уравнение прямой, проходящей через точку М=<15; 4> перпендикулярно

Найдем координаты нормали к гиперболе в точке М.

Уравнение прямой, проходящей через точку М0(х0;у0) перпендикулярно вектору П = <A, B>, имеет вид:

А(х – х0) + В(у – у0) = 0.

Запишем уравнение касательной:

Ответ: Уравнение касательной:

Составить уравнение параболы, если даны ее фокус F(2; -1) и директриса

Используйте определение параболы: параболой называется геометрическое место точек, для каждой из которых расстояние до фокуса равно расстоянию до директрисы.

Используем определение параболы:

Параболой называется геометрическое место точек, для каждой из которых расстояние до фокуса равно расстоянию до директрисы.

Пусть точка М(Х, У) лежит на параболе. Тогда ее расстояние до фокуса

Выразим через Х и У расстояние от точки М до директрисы.

Нормальное уравнение директрисы:

Из определения параболы DM = MF,

Ответ: уравнение параболы: Х2 + 2Ху + У2 – 6Х + 2У + 9 = 0.

Составить уравнение параболы с вершиной в начале координат, если известно, что парабола симметрична относительно оси Ох и проходит через точку А=<9; 6>. Найти координаты ее фокуса.

Из условий задачи следует, что данная парабола задается каноническим уравнением

Подставьте в это уравнение координаты точки А и найдите значение параметра Р параболы.

Из условий задачи следует, что данная парабола задается каноническим уравнением

Подставим в это уравнение координаты точки А: 36 = 2Р·9, откуда Р = 2.

Следовательно, уравнение параболы имеет вид: У2 = 4Х.

Координаты фокуса параболы задаются формулой: F=<0,5P; 0>, то есть F=<1; 0>.

Ответ: уравнение параболы: У2 = 4Х; фокус F=<1; 0>.