Для несжимаемой жидкости уравнение имеет вид

Уравнение Навье-Стокса и симуляция жидкостей на CUDA

Привет, Хабр. В этой статье мы разберемся с уравнением Навье-Стокса для несжимаемой жидкости, численно его решим и сделаем красивую симуляцию, работающую за счет параллельного вычисления на CUDA. Основная цель — показать, как можно применить математику, лежащую в основе уравнения, на практике при решении задачи моделирования жидкостей и газов.

Уравнение Навье-Стокса для несжимаемой жидкости

Я думаю каждый хоть раз слышал об этом уравнении, некоторые, быть может, даже аналитически решали его частные случаи, но в общем виде эта задачи остается неразрешенной до сих пор. Само собой, мы не ставим в этой статье цель решить задачу тысячелетия, однако итеративный метод применить к ней мы все же можем. Но для начала, давайте разберемся с обозначениями в этой формуле.

Условно уравнение Навье-Стокса можно разделить на пять частей:

• — обозначает скорость изменения скорости жидкости в точке (его мы и будем считать для каждой частицы в нашей симуляции).
• — перемещение жидкости в пространстве.
• — давление, оказываемое на частицу (здесь — коэффициент плотности жидкости).
• — вязкость среды (чем она больше, тем сильнее жидкость сопротивляется силе, применяемой к ее части), — коэффициент вязкости).
• — внешние силы, которые мы применяем к жидкости (в нашем случае сила будет играть вполне конкретную роль — она будет отражать действия, совершаемые пользователем.

Также, так как мы будем рассматривать случай несжимаемой и однородной жидкости, мы имеем еще одно уравнение: . Энергия в среде постоянна, никуда не уходит, ниоткуда не приходит.

Будет неправильно обделить всех читателей, которые не знакомы с векторным анализом, поэтому заодно и бегло пройдемся по всем операторам, присутствующим в уравнении (однако, настоятельно рекомендую вспомнить, что такое производная, дифференциал и вектор, так как они лежат в основе всего того, о чем пойдет речь ниже).

Начнем мы с с оператора набла, представляющего из себя вот такой вектор (в нашем случае он будет двухкомпонентным, так как жидкость мы будет моделировать в двумерном пространстве):

Оператор набла представляет из себя векторный дифференциальный оператор и может быть применен как к скалярной функции, так и к векторной. В случае скаляра мы получаем градиент функции (вектор ее частных производных), а в случае вектора — сумму частых производных по осям. Главная особенность данного оператора в том, что через него можно выразить основные операции векторного анализа — grad (градиент), div (дивергенция), rot (ротор) и (оператор Лапласа). Стоит сразу же отметить, что выражение не равносильно — оператор набла не обладает коммутативностью.

Как мы увидим далее, эти выражения заметно упрощаются при переходе на дискретное пространство, в котором мы и будем проводить все вычисления, так что не пугайтесь, если на данный момент вам не очень понятно, что же со всем этим делать. Разбив задачу на несколько частей, мы последовательно решим каждую из них и представим все это в виде последовательного применения нескольких функций к нашей среде.

Численное решение уравнения Навье-Стокса

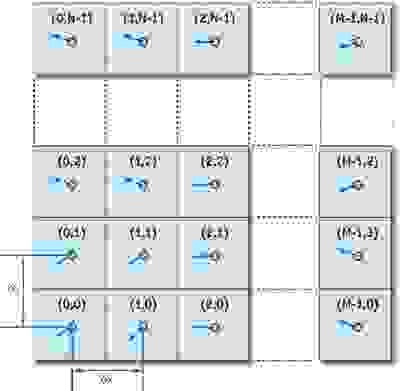
Чтобы представить нашу жидкость в программе, нам необходимо получить математическую репрезентацию состояния каждой частицы жидкости в произвольный момент времени. Самый удобный для этого метод — создать векторное поле частиц, хранящее их состояние, в виде координатной плоскости:

В каждой ячейке нашего двумерного массива мы будем хранить скорость частицы в момент времени , а расстояние между частицами обозначим за и соответственно. В коде же нам будет достаточно изменять значение скорости каждую итерацию, решая набор из нескольких уравнений.

Теперь выразим градиент, дивергенцию и оператор Лапласа с учетом нашей координатной сетки ( — индексы в массиве, — взятие соответствующих компонентов у вектора):

Оператор	Определение	Дискретный аналог
grad
div
rot

Мы можем еще сильнее упростить дискретные формулы векторных операторов, если положим, что . Данное допущение не будет сильно сказываться на точности алгоритма, однако уменьшает количество операций на каждую итерацию, да и в целом делает выражения приятней взгляду.

Перемещение частиц

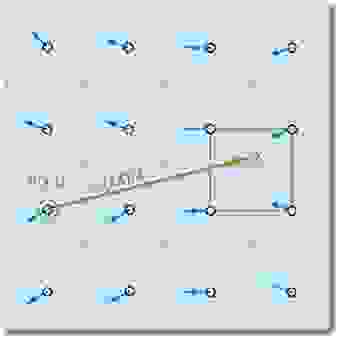
Данные утверждения работают только в том случае, если мы можем найти ближайшие частицы относительно рассматриваемой на данный момент. Чтобы свести на нет все возможные издержки, связанные с поиском таковых, мы будет отслеживать не их перемещение, а то, откуда приходят частицы в начале итерации путем проекции траектории движения назад во времени (проще говоря, вычитать вектор скорости, помноженный на изменение времени, из текущей позиции). Используя этот прием для каждого элемента массива, мы будем точно уверены, что у любой частицы будут «соседи»:

Положив, что — элемент массива, хранящий состояния частицы, получаем следующую формулу для вычисления ее состояния через время (мы полагаем, что все необходимые параметры в виде ускорения и давления уже рассчитаны):

Заметим сразу же, что при достаточно малом и скорости мы можем так и не выйти за пределы ячейки, поэтому очень важно правильно подобрать ту силу импульса, которую пользователь будет придавать частицам.

Чтобы избежать потери точности в случае попадания проекции на границу клеток или в случае получения нецелых координат, мы будем проводить билинейную интерполяцию состояний четырех ближайших частиц и брать ее за истинное значение в точке. В принципе, такой метод практически не уменьшит точность симуляции, и вместе с тем он достаточно прост в реализации, так что его и будем использовать.

Вязкость

. В таком случае итеративное уравнение для скорости примет следующий вид:

Мы несколько преобразуем данное равенство, приведя его к виду (стандартный вид системы линейных уравнений):

где — единичная матрица. Такие преобразования нам необходимы, чтобы в последствии применить метод Якоби для решения нескольких схожих систем уравнений. Его мы также обсудим в дальнейшем.

Внешние силы

Импульс-вектор легко посчитать как разность между предыдущей позицией мыши и текущей (если такая имелась), и здесь как раз-таки можно проявить креативность. Именно в этой части алгоритма мы можем внедрить добавление цветов в жидкость, ее подсветку и т.п. К внешним силам также можно отнести гравитацию и температуру, и хоть реализовать такие параметры несложно, в данной статье рассматривать их мы не будем.

Давление

Давление в уравнении Навье-Стокса — та сила, которая препятствует частицам заполнять все доступное им пространство после применения к ним какой-либо внешней силы. Сходу его расчет весьма затруднителен, однако нашу задачу можно значительно упростить, применив теорему разложения Гельмгольца.

Назовем векторное поле, полученное после расчета перемещения, внешних сил и вязкости. Оно будет иметь ненулевую дивергенцию, что противоречит условию несжимаемости жидкости (), и чтобы это исправить, необходимо рассчитать давление. Согласно теореме разложения Гельмгольца, можно представить как сумму двух полей:

где — и есть искомое нами векторное поле с нулевой дивергенцией. Доказательство этого равенства в данной статье приводиться не будет, однако в конце вы сможете найти ссылку с подробным объяснением. Мы же можем применить оператор набла к обоим частям выражения, чтобы получить следующую формулу для расчета скалярного поля давления:

Записанное выше выражение представляет из себя уравнение Пуассона для давления. Его мы также можем решить вышеупомянутым методом Якоби, и тем самым найти последнюю неизвестную переменную в уравнении Навье-Стокса. В принципе, системы линейных уравнений можно решать самыми разными и изощренными способами, но мы все же остановимся на самом простом из них, чтобы еще больше не нагружать данную статью.

Граничные и начальные условия

Любое дифференциальное уравнение, моделируемое на конечной области, требует правильно заданных начальных или граничных условий, иначе мы с очень большой вероятностью получим физически неверный результат. Граничные условия устанавливаются для контролирования поведения жидкости близ краев координатной сетки, а начальные условия задают параметры, которые имеют частицы в момент запуска программы.

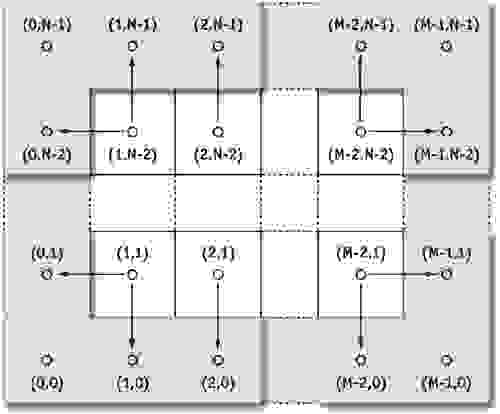
Начальные условия будут весьма простыми — изначально жидкость неподвижна (скорость частиц равна нулю), и давление также равно нулю. Граничные условия будут задаваться для скорости и давления приведенными формулами:

Тем самым, скорость частиц на краях будет противоположна скорости у краев (тем самым они будут отталкиваться от края), а давление равно значению непосредственно рядом с границей. Данные операции следует применить ко всем ограничивающим элементам массива (к примеру, есть размер сетки , то алгоритм мы применим для клеток, отмеченных на рисунке синим):

Краситель

В формуле отвечает за пополнение красителем области (возможно, в зависимости от того, куда нажмет пользователь), непосредственно является количество красителя в точке, а — коэффициент диффузии. Решить его не составляет большого труда, так как вся основная работа по выводу формул уже проведена, и достаточно лишь сделает несколько подстановок. Краску можно реализовать в коде как цвет в формате RGB, и в таком случае задача сводится к операциям с несколькими вещественными величинами.

Завихренность

есть результат применения ротора к вектору скорости (его определение дано в начале статьи), — градиент скалярного поля абсолютных значений . представляет нормализованный вектор , а — константа, контролирующая, насколько большими будут завихренности в нашей жидкости.

Метод Якоби для решения систем линейных уравнений

Для нас — элементы массива, представляющие скалярное или векторное поле. — номер итерации, его мы можем регулировать, чтобы как увеличить точность расчета или наоборот уменьшить, и повысить производительность.

Для расчет вязкости подставляем: , , , здесь параметр — сумма весов. Таким образом, нам необходимо хранить как минимум два векторных поля скоростей, чтобы независимо считать значения одного поля и записывать их в другое. В среднем, для расчета поля скорости методом Якоби необходимо провести 20-50 итераций, что весьма много, если бы мы выполняли вычисления на CPU.

Для уравнения давления мы сделаем следующую подстановку: , , , . В результате мы получим значение в точке. Но так как оно используется только для расчета градиента, вычитаемого из поля скорости, дополнительные преобразования можно не выполнять. Для поля давления лучше всего выполнять 40-80 итераций, потому что при меньших числах расхождение становится заметным.

Реализация алгоритма

Реализовывать алгоритм мы будем на C++, также нам потребуется Cuda Toolkit (как его установить вы можете прочитать на сайте Nvidia), а также SFML. CUDA нам потребуется для распараллеливания алгоритма, а SFML будет использоваться только для создания окна и отображения картинки на экране (В принципе, это вполне можно написать на OpenGL, но разница в производительности будет несущественна, а вот код увеличится еще строк на 200).

Cuda Toolkit

Сначала мы немного поговорим о том, как использовать Cuda Toolkit для распараллеливания задач. Более подробный гайд предоставляется самой Nvidia, поэтому здесь мы ограничимся только самым необходимым. Также предполагается, что вы смогли установить компилятор, и у вас получилось собрать тестовый проект без ошибок.

Чтобы создать функцию, исполняющуюся на GPU, для начала необходимо объявить, сколько ядер мы хотим использовать, и сколько блоков ядер нужно выделить. Для этого Cuda Toolkit предоставляет нам специальную структуру — dim3, по умолчанию устанавливающую все свои значения x, y, z равными 1. Указывая ее как аргумент при вызове функции, мы можем управлять количеством выделяемых ядер. Так как работаем мы с двумерным массивом, то в конструкторе необходимо установить только два поля: x и y:

где size_x и size_y — размер обрабатываемого массива. Сигнатура и вызов функции выглядят следующим образом (тройные угловые скобки обрабатываются компилятором Cuda):

В самой функции можно восстановить индексы двумерного массива через номер блока и номер ядра в этом блоке по следующей формуле:

Следует отметить, что функция, исполняемая на видеокарте, должна быть обязательно помечена тегом __global__ , а также возвращать void, поэтому чаще всего результаты вычислений записываются в передаваемый как аргумент и заранее выделенный в памяти видеокарты массив.

За освобождение и выделение памяти на видеокарте отвечают функции CudaMalloc и CudaFree. Мы можем оперировать указателями на область памяти, которые они возвращают, но получить доступ к данным из основного кода не можем. Самый простой способ вернуть результаты вычислений — воспользоваться cudaMemcpy, схожей со стандартным memcpy, но умеющей копировать данные с видеокарты в основную память и наоборот.

SFML и рендер окна

Вооружившись всеми этими знаниями, мы наконец можем перейти к непосредственному написанию кода. Для начала давайте создадим файл main.cpp и разместим туда весь вспомогательный код для рендера окна:

строка в начале функции main

создает изображение формата RGBA в виде одномерного массива с константной длиной. Его мы будем передавать вместе с другими параметрами (позиция мыши, разница между кадрами) в функцию computeField. Последняя, как и несколько других функций, объявлены в kernel.cu и вызывают код, исполняемый на GPU. Документацию по любой из функций вы можете найти на сайте SFML, в коде файла не происходит ничего сверхинтересного, поэтому мы не будем надолго на нем останавливаться.

Вычисления на GPU

Чтобы начать писать код под gpu, для начала создадим файл kernel.cu и определим в нем несколько вспомогательных классов: Color3f, Vec2, Config, SystemConfig:

Атрибут __host__ перед именем метода означает, что код может исполнятся на CPU, __device__ , наоборот, обязует компилятор собирать код под GPU. В коде объявляются примитивы для работы с двухкомпонентными векторами, цветом, конфиги с параметрами, которые можно менять в рантайме, а также несколько статических указателей на массивы, которые мы будем использовать как буферы для вычислений.

cudaInit и cudaExit также определяеются достаточно тривиально:

В функции инициализации мы выделяем память под двумерные массивы, задаем массив цветов, которые мы будем использовать для раскраски жидкости, а также устанавливаем в конфиг значения по умолчанию. В cudaExit мы просто освобождаем все буферы. Как бы это парадоксально не звучало, для хранения двумерных массивов выгоднее всего использовать одномерные, обращение к которым будет осуществляться таким выражением:

Начнем реализацию непосредственного алгоритма с функции перемещения частиц. В advect передаются поля oldField и newField (то поле, откуда берутся данные и то, куда они записываются), размер массива, а также дельта времени и коэффициент плотности (используется для того, чтобы ускорить растворение красителя в жидкости и сделать среду не сильно чувствительной к действиям пользователя). Функция билинейной интерполяции реализована классическим образом через вычисление промежуточных значений:

Функцию диффузии вязкости было решено разделить на несколько частей: из главного кода вызывается computeDiffusion, которая вызывает diffuse и computeColor заранее указанное число раз, а затем меняет местами массив, откуда мы берем данные, и тот, куда мы их записываем. Это самый простой способ реализовать параллельную обработку данных, но мы расходует в два раза больше памяти.

Обе функции вызывают вариации метода Якоби. В теле jacobiColor и jacobiVelocity сразу же идет проверка, что текущие элементы не находятся на границе — в этом случае мы должны установить их в соответствии с формулами, изложенными в разделе Граничные и начальные условия.

Применение внешней силы реализовано через единственную функцию — applyForce, принимающую как аргументы позицию мыши, цвет красителя, а также радиус действия. С ее помощью мы можем придать скорость частицам, а также красить их. братная экспонента позволяет сделать область не слишком резкой, и при этом достаточно четкой в указанном радиусе.

Расчет завихренности представляет из себя уже более сложный процесс, поэтому его мы реализуем в computeVorticity и applyVorticity, заметим также, что для них необходимо определить два таких векторных оператора, как curl (ротор) и absGradient (градиент абсолютных значений поля). Чтобы задать дополнительные эффекты вихря, мы умножаем компоненту вектора градиента на , а затем нормализируем его, разделив на длину (не забыв при этом проверить, что вектор ненулевой):

Следующим этапом алгоритма будет вычисление скалярного поля давления и его проекция на поле скорости. Для этого нам потребуется реализовать 4 функции: divergency, которая будет считать дивергенцию скорости, jacobiPressure, реализующую метод Якоби для давления, и computePressure c computePressureImpl, проводящие итеративные вычисления поля:

Проекция умещается в две небольшие функции — project и вызываемой ей gradient для давления. Это, можно сказать, последний этап нашего алгоритма симуляции:

После проекции мы смело можем перейти к отрисовке изображения в буфер и различным пост-эффектам. В функции paint выполняется копирование цветов из поля частиц в массив RGBA. Также была реализована функция applyBloom, которая подсвечивает жидкость, когда на нее наведен курсор и нажата клавиша мыши. Из опыта, такой прием делает картину более приятной и интересной для глаз пользователя, но он вовсе не обязателен.

В постобработке также можно подсвечивать места, в которых жидкость имеет наибольшую скорость, менять цвет в зависимости от вектора движения, добавлять различные эффекты и прочее, но в нашем случае мы ограничимся своеобразным минимумом, ведь даже с ним изображения получаются весьма завораживающими (особенно в динамике):

И под конец у нас осталась одна главная функция, которую мы вызываем из main.cpp — computeField. Она сцепляет воедино все кусочки алгоритма, вызывая код на видеокарте, а также копирует данные с gpu на cpu. В ней же находится и расчет вектора импульса и выбор цвета красителя, которые мы передаем в applyForce:

Заключение

В этой статье мы разобрали численный алгоритм решения уравнения Навье-Стокса и написали небольшую программу-симуляцию для несжимаемой жидкости. Быть может мы и не разобрались во всех тонкостях, но я надеюсь, что материал оказался для вас интересным и полезным, и как минимум послужил хорошим введением в область моделирования жидкостей.

Как автор данной статьи, я буду искренне признателен любым комментариям и дополнениям, и постараюсь ответить на все возникшие у вас вопросы под этим постом.

Дополнительный материал

Весь исходный код, приведенный в данной статье, вы можете найти в моем Github-репозитории. Любые предложения по улучшению приветствуются.

Оригинальный материал, послуживший основой для данной статьи, вы можете прочесть на официальном сайте Nvidia (англ). В нем также представлены примеры реализации частей алгоритма на языке шейдеров:
developer.download.nvidia.com/books/HTML/gpugems/gpugems_ch38.html

Доказательство теоремы разложения Гельмгольца и огромное количество дополнительного материала про механику жидкостей можно найти в данной книге (англ, см. раздел 1.2):
Chorin, A.J., and J.E. Marsden. 1993. A Mathematical Introduction to Fluid Mechanics. 3rd ed. Springer.

Канал одного англоязычного ютубера, делающего качественный контент, связанной с математикой, и решением дифференциальных уравнений в частности (англ). Очень наглядные ролики, помогающие понять суть многих вещей в математике и физике:
3Blue1Brown — YouTube
Differential Equations (3Blue1Brown)

Также выражаю благодарность WhiteBlackGoose за помощь в подготовке материала для статьи.

И под конец небольшой бонус — несколько красивых скриншотов, снятых в программе:

Прямой поток (дефолтные настройки)

Водоворот (большой радиус в applyForce)

Волна (высокая завихренность + диффузия)

Также по многочисленным просьбам добавил видео с работой симуляции:

Уравнение Бернулли

Уравнение Бернулли для струйки жидкости формулируется следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.

Уравнение Бернулли выглядит так:

Подробное описание всех входящих в состав уравнения параметров уже описан в этой статье.

Содержание статьи

Смысл уравнения Бернулли

По существу вывода уравнение Бернулли для струйки идеальной жидкости представляет собой закон сохранения механической энергии, составленный применительно к единице массового расхода жидкости. Это следует из того, что в процессе вывода значения работы сил, приложенных к выделенному объему струйки и значения кинетической энергии этого объема были поделены на величину ρqΔT.

Отсюда вытекает, что поскольку член υ 2 /2 является мерой кинетической энергии единицы массы движущейся жидкости, то сумма членов gz+p/ρ будет мерилом ее потенциальной энергии.

В отношении величины gz это очевидно, ведь если частица жидкости массы m расположена на высоте z относительно некоторой плоскости и находится под действием сил тяжести, то способность ее совершить работу, т.е. её потенциальная энергия относительно этой плоскости равняется mgz. Но если её поделить на массу частиц m, то эта часть потенциальной энергии даст величину gz.

Для более ясного физического представления о том, что потенциальная энергия измеряется величиной p/ρ рассмотрим такую схему: пусть к трубе, заполненной жидкостью с избыточным давлением p, присоединен пьезометр, снабженный на входе в него краном.

Кран сначала закрыт, т.е. пьезометр свободен от жидкости, а элементарный объем жидкости ΔV массой ρ*ΔV перед краном находится под давлением p.

Если затем открыть кран, то жидкость в пьезометре поднимется на некоторую высоту, равную

Таким образом, единица массы, находящейся под давлением p, как бы несет в себе ещё заряд потенциальной энергии, определяемой величиной p/ρ.

В гидравлике для характеристики удельной энергии обычно используется понятие напор, под которым понимают энергию жидкости, отнесенную к единице силы тяжести, а не её массы. В соответствии с этим уравнение Бернулли записанное в начале этой статьи примет вид

Такое уравнение Бернулли для элементарной струйки идеальной жидкости в другой форме, весьма удобно для гидравлических расчетов и может быть сформулировано следующим образом.

Для элементарной струйки идеальной жидкости полный напор, т.е. сумма геометрического, пьезометрического и скоростного напоров, есть величина постоянная во всех её сечениях.

Отсюда следует, что между напором и удельной энергией существует очень простая зависимость

где э – удельная энергия

Уравнение Бернулли для элементарной струйки реальной жидкости

Если вместо идеальной жидкости рассматривать жидкость реальную, то уравнение Бернулли для реальной жидкости должно принять несколько другой вид.

При движении идеальной жидкости её полная удельная энергия или напор сохраняет постоянное значение по длине струйки, а при движении реальной жидкости эта энергия будет убывать по направлению движения. Причиной этого являются затраты энергии на преодоление сопротивлений движению, обусловленные внутренним трением в вязкой жидкости.

Если же мы рассмотрим два сечения для струйки идеальной жидкости: 1-1 в начале и 2-2 в конце струйки, то полная удельная энергия будет

Полная удельная энергия для сечения 1-1 всегда будет больше, чем полная удельная энергия для сечения 2-2 на некоторую величину потерь, и уравнение Бернулли в этом случае получается

Величина Э_1-2 представляет собой меру энергии, потерянную единицей массы жидкости на преодоление сопротивлений при её движениями между указанными сечениями.

Соответствующий этой потере удельной энергии напор называют потерей напора между сечениями 1-1 и 2-2 и обозначают h_1-2 . Поэтому уравнение Бернулли для элементарной струйки реальной жидкости можно представить в виде

Уравнение Бернулли для потока реальной жидкости

Уравнение Бернулли для струйки реальной жидкости это еще только половина дела, ведь в при решении различных практических вопросов о движении жидкостей приходится иметь дело с потоками конечных размеров. Уравнение Бернулли в этом случае может быть получено, исходя из рассмотрения потока как совокупности множества элементарных струек.

Учитывая, что все струйки движутся с одной и той же средней скоростью форма записи уравнения Бернулли для потока идеальной жидкости становится идентичной его записи для элементарной струйки.

В таком виде уравнение Бернулли обычно и применяется при решении практических задач для потоков однородной несжимаемой жидкости при установившемся движении, происходящем под действием одной силы тяжести.

Такое уравнение составляется для различных живых сечений потока, вблизи которых движение жидкости должно удовлетворять условиям медленно изменяющегося движения, хотя на пути между этими сечениями движение может и не удовлетворять указанным условиям.

Слагаемое h_1-2 в этом уравнении показывает потери напора на преодоление сопротивлений движению жидкости. При этом в гидравлике различают два основных вида сопротивлений:
— h_лп — линейные потери — сопротивления, проявляющиеся по всей длине потока, обусловленные силами трения частиц жидкости друг о друга и о стенки, ограничивающие поток.
— h_мп — местные потери – местные сопротивления, обусловленные различного рода препятствиями, устанавливаемыми в потоке (задвижка, кран, колено), приводящими к изменениям величины или направления скорости течения жидкости

Поэтому полная потеря напора между двумя сечениями потока при наличии сопротивлений обоих видов будет

Видео по теме

Уравнение Бернулли подходит и для газов. Явление уменьшения давления при повышении скорости потока является основой работы различных приборов для измерения расхода. Закон Бернулли справедлив и для жидкостей вязкость которых равна нулю. При описании течения таких жидкостей используют уравнение Бернулли с добавлением слагаемых учитывающих потери на местные сопротивления.

Основы гидравлики

Уравнение Бернулли — фундамент гидродинамики

Бернулли — вне всякого сомнения — имя, знакомое и специалистам, и обывателям, которые хоть немного интересуются науками. Этот человек оставил ослепительный след в истории познавания человечеством окружающего мира, как физик, механик, гидравлик и просто общепризнанный гений, Даниил Бернулли навсегда останется в памяти благодарных потомков за свои идеи и выводы, которые долгое время существования человечества были покрыты мраком неизведанного.
Открытия и законы, которыми Бернулли осветил путь к познанию истины, являются фундаментальными, и придали ощутимый импульс развитию многих естественных наук. К таковым относится и уравнение Бернулли в Гидравлике, которое он вывел почти три века назад. Данное уравнение является основополагающим законом этой сложной науки, объясняющим многие явления, описанные даже древними учеными, например, великим Архимедом.

Попробуем уяснить несложную суть закона Бернулли (чаще его называют уравнением Бернулли), описывающего поведение жидкости в той или иной ситуации.

Выделим в стационарно текущей идеальной жидкости трубку тока, которая ограничена сечениями S₁ и S₂ , (рис. 1) .
(Понятие идеальной жидкости абстрактно, как и понятие всего идеального. Идеальной считается жидкость, в которой нет сил внутреннего трения, т. е. трения между отдельными слоями и частицами подвижной жидкости).
Пусть в месте сечения S₁ скорость течения ν₁ , давление p₁ и высота, на которой это сечение расположено, h₁ . Аналогично, в месте сечения S₂ скорость течения ν₂ , давление p₂ и высота сечения h₂ .

За бесконечно малый отрезок времени Δt жидкость переместится от сечения S₁ к сечению S₁‘ , от S₂ к S₂‘ .

По закону сохранения энергии, изменение полной энергии E₂ — E₁ идеальной несжимаемой жидкости равно работе А внешних сил по перемещению массы m жидкости:

где E₁ и E₂ — полные энергии жидкости массой m в местах сечений S₁ и S₂ соответственно.

С другой стороны, А — это работа, которая совершается при перемещении всей жидкости, расположенной между сечениями S₁ и S₂ , за рассматриваемый малый отрезок времени Δt .
Чтобы перенести массу m от S₁ до S₁‘ жидкость должна переместиться на расстояние L₁ = ν₁Δt и от S₂ до S₂‘ — на расстояние L₂ = ν₂Δt . Отметим, что L₁ и L₂ настолько малы, что всем точкам объемов, закрашенных на рис. 1 , приписывают постоянные значения скорости ν , давления р и высоты h .
Следовательно,

где F₁ = p₁S₁ и F₂ = — p₂S₂ (сила отрицательна, так как направлена в сторону, противоположную течению жидкости; см. рис. 1).

Полные энергии E₁ и E₂ будут складываться из кинетической и потенциальной энергий массы m жидкости:

Подставляя (3) и (4) в (1) и приравнивая (1) и (2) , получим

Согласно уравнению неразрывности для несжимаемой жидкости, объем, занимаемый жидкостью, всегда остается постоянным, т. е.

Разделив выражение (5) на ΔV , получим

где ρ — плотность жидкости.

После некоторых преобразований эту формулу можно представить в другом виде:

Поскольку сечения выбирались произвольно, то в общем случае можно записать:

ρv 2 /2 +ρgh +p = const (6) .

Выражение (6) получено швейцарским физиком Д. Бернулли (опубликовано в 1738 г.) и называется уравнением Бернулли.

Даниил Бернулли (Daniel Bernoulli, 1700 — 1782), швейцарский физик, механик и математик, один из создателей кинетической теории газов, гидродинамики и математической физики. Академик и иностранный почётный член (1733) Петербургской академии наук, член Академий: Болонской (1724), Берлинской (1747), Парижской (1748), Лондонского королевского общества (1750).

Уравнение Бернулли по своей сути является интерпретацией закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Уравнение хорошо выполняется и для реальных жидкостей, для которых внутреннее трение не очень велико.

Величина р в формуле (6) называется статическим давлением (давление жидкости на поверхность обтекаемого ею тела) , величина ρν 2 /2 — динамическим давлением, величина ρgh — гидростатическим давлением.

Статическое давление обусловлено взаимодействием поверхности жидкости с внешней средой и является составляющей внутренней энергии рассматриваемого элементарного объема жидкости (т. е. характеризуется взаимодействием внутренних частиц жидкости, вызванных внешним возмущением — давлением) , а гидростатическое – положением этого объема жидкости в пространстве (зависит от высоты над поверхностью Земли) .
Динамическое давление характеризует кинематическую составляющую энергии этого объема, поскольку зависит от скорости потока, в котором движется рассматриваемый элементарный объем жидкости.

Для горизонтальной трубки тока изменение потенциальной составляющей ρgh будет равно нулю (поскольку h2 – h1 = 0) , и выражение (6) примет упрощенный вид:

ρv 2 /2 + p = const (7) .

Выражение p + ρν 2 /2 называется полным давлением.

Таким образом, содержание уравнения Бернулли для элементарной струйки при установившемся движении можно сформулировать так: удельная механическая энергия при установившемся движении элементарной струйки идеальной жидкости, представляющая собой сумму удельной потенциальной энергии положения и давления и удельной кинетической энергии, есть величина постоянная.

Все члены уравнения Бернулли измеряются в линейных единицах.

В гидравлике широко применяют термин напор, под которым подразумевают механическую энергию жидкости, отнесенную к единице ее веса (удельную энергию потока или неподвижной жидкости) .
Величину v 2 /2g называют скоростным (кинетическим) напором, показывающим, на какую высоту может подняться движущаяся жидкость за счет ее кинетической энергии.
Величину h_п = p/ρg называют пьезометрическим напором, показывающим на какую высоту поднимается жидкость в пьезометре под действием оказываемого на нее давления.
Величину z называют геометрическим напором, характеризующим положение центра тяжести соответствующего сечения движущейся струйки над условно выбранной плоскостью сравнения.

Сумму геометрического и пьезометрического напоров называют потенциальным напором, а сумму потенциального и скоростного напора — полным напором.

На основании анализа уравнения Бернулли можно сделать вывод, что при прочих неизменных параметрах потока (жидкости или газа) величина давления в его сечениях обратно пропорциональна скорости, т. е. чем выше давление, тем меньше скорость, и наоборот.
Это явление используется во многих технических конструкциях и устройствах, например, в карбюраторе автомобильного двигателя (диффузор), в форме крыла самолета. Увеличение скорости воздушного потока в диффузоре карбюратора приводит к созданию разрежения, всасывающего бензин из поплавковой камеры, а специальная форма сечения самолетного крыла позволяет создавать на его нижней стороне зону повышенного давления, способствующего появлению подъемной силы.

Геометрическая интерпретация уравнения Бернулли

Поскольку напор измеряется в линейных величинах, можно дать графическую (геометрическую) интерпретацию уравнению Бернулли и его составляющим.

На графике (рис. 2) представлена горизонтальная плоскость сравнения 0-0 , относительно которой геометрический напор будет в каждом сечении равен вертикальной координате z центра тяжести сечения (линия геометрического напора проходит по оси струйки) .
Линия К-К , характеризующая потенциальный напор струйки, получена сложением геометрического и пьезометрического напора в соответствующих сечениях (т. е. разница координат точек линии К-К и соответствующих точек оси струйки характеризует пьезометрический напор в данном сечении) .
Полный напор характеризуется линией MN , которая параллельна плоскости сравнения О-О , свидетельствуя о постоянстве полного напора H’_e (удельной механической энергии) идеальной струйки в любом ее сечении.

При движении реальной жидкости, обладающей вязкостью, возникают силы трения между ограничивающими поток поверхностями и между слоями внутри самой жидкости. Для преодоления этих сил трения расходуется энергия, которая превращается в теплоту и рассеивается в дальнейшем движущейся жидкостью. По этой причине графическое изображение уравнения Бернулли для идеальной жидкости будет отличаться от аналогичного графика для реальной жидкости.
Если обозначить h_f потери напора (удельной энергии) струйки на участке длиной L , то уравнение Бернулли для реальной жидкости примет вид:

Для реальной жидкости полный напор вдоль струйки не постоянен, а убывает по направлению течения жидкости, т. е. его графическая интерпретация имеет вид не прямой линии, а некоторой кривой МЕ (рис. 3) . Заштрихованная область характеризует потери напора.

Падение напора на единице длины элементарной струйки, измеренной вдоль оси струйки, называют гидравлическим уклоном:

Гидравлический уклон положителен, если напорная линия снижается по течению жидкости, что всегда бывает при установившемся движении.

Для практического применения уравнения Бернулли необходимо распространить его на поток реальной жидкости:

где α₁ , α₂ — коэффициенты Кориолиса, учитывающие различие скоростей в разных точках сечения потока реальной жидкости.
На практике обычно принимают α₁ = α₂ = α : для ламинарного режима течения жидкости в круглых трубах α = 2, для турбулентного режима α = 1,04. 1,1.

Из уравнения Бернулли для горизонтальной трубки тока и уравнения неразрывности ( S₁v₁Δt = S₂v₂Δt ) видно, что при течении жидкости по горизонтальной трубе, которая имеет различные сечения, скорость жидкости больше в более узких местах (где площадь сечения S меньше) , а статическое давление больше в более широких местах, т. е. там, где скорость меньше. Это можно увидеть, установив вдоль трубы ряд манометров.

Данный опыт показывает, что в манометрической трубке В , которая прикреплена к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С , которые прикреплены к широкой части трубы, что соответствует уравнению Бернулли.

Так как динамическое давление зависит от скорости движения жидкости (газа) , то уравнение Бернулли можно использовать для измерения скорости потока жидкости. Принципиально это свойство жидкости для определения скорости потока реализовано в так называемой трубке Пито – Прандтля (обычно ее называют трубкой Пито ) .

Трубка Пито – Прандтля ( см. рис. 2 ) состоит из двух тонких стеклянных трубок, одна из которых изогнута под прямым углом (Г-образно) , а вторая — прямая.
Одним из свободных концов каждая трубка присоединена к манометру.
Изогнутая трубка имеет открытый свободный конец, направленный против тока и принимающий напор потока жидкости, а вторая погружена в поток перпендикулярно току, и скорость потока на давление внутри трубки не влияет, т. е. внутри этой трубки действует лишь статическая составляющая давления жидкости.
Разница между давлением в первой трубке (полное давление) и второй трубке (статическое давление) , которую показывает манометр, является динамическим давлением, определяемым по формуле:

Определив с помощью трубки Пито — Прандтля динамическое давление в потоке жидкости, можно легко вычислить скорость этого потока:

Уравнение Бернулли также используют для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью, с маленьким отверстием в боковой стенке на некоторой глубине ниже уровня жидкости.

Рассмотрим два сечения (на уровне h₁ свободной поверхности жидкости в сосуде и на уровне h₁ выхода ее из отверстия) и применим уравнение Бернулли:

Так как давления р₁ и р₂ в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. р₁ = р₂ , то уравнение будет иметь вид

Из уравнения неразрывности мы знаем, что ν₁/ν₂ = S₂/S₁ , где S₁ и S₂ — площади поперечных сечений сосуда и отверстия.
Если S₁ значительно превышает S₂ , то слагаемым ν₁ 2 /2 можно пренебречь и тогда:

Это выражение получило название формулы Торричелли.
Формулу Торричелли можно использовать для подсчета объемного (или массового) расхода жидкости, истекающего из отверстия в сосуде с поддерживаемым постоянно уровнем под действием атмосферного давления.
При этом используется формула Q = vS (для определения массового расхода – m = ρvS ) , по которой определяется расход жидкости за единицу времени.

Если требуется узнать расход жидкости за определенный промежуток времени t , то его определяют, умножив расход за единицу времени на время t .

Следует отметить, что такая методика расчета расхода реальной жидкости через отверстие в стенке сосуда дает некоторые погрешности, обусловленные физическими свойствами реальных жидкостей, поэтому требует применения поправочных коэффициентов (коэффициентов расхода) .

Пример решения задачи на определение расхода жидкости

Определить примерный объемный расход воды, истекающей из отверстия диаметром 10 мм, проделанном в вертикальной стенке широкого сосуда на высоте h = 1 м от верхнего, постоянно поддерживаемого, уровня воды за 10 секунд.
Ускорение свободного падения принять равным g = 10 м/с 2 .
Коэффициент расхода воды через отверстие — µ_s = 0,62.

По формуле Торричелли определим скорость истечения воды из отверстия:

v = √2gh = √2×10×1 ≈ 4,5 м/с.

Определим расход воды Q за время t = 10 секунд:

Q = µ_svSt = 0,62×4,5×3,14×0,012/4 × 10 ≈ 0,0022 м 3 ≈ 2,2 литра.

На практике расход жидкости в трубопроводах измеряют расходомерами, например, расходомером Вентури. Расходомер Вентури (см рис. 2) представляет собой конструкцию из двух конических патрубков, соединенных цилиндрическим патрубком. В сечениях основной трубы и цилиндрического патрубка устанавливают трубки-пьезометры, которые фиксируют уровень жидкости, обусловленный полным давлением в потоке.

При прохождении жидкости через сужающийся конический патрубок часть потенциальной энергии потока преобразуется в кинетическую, и, наоборот, – при прохождении потока по расширяющемуся коническому патрубку, кинетическая энергия уменьшается, а потенциальная растет. Это сказывается на скорости движения жидкости по рассматриваемым участкам. Перепад высоты уровня жидкости в пьезометрах позволяет рассчитать среднюю скорость потока жидкости на рассматриваемых участках и вычислить объемный расход по внутреннему сечению трубы.
В расходомерах учитываются потери напора в самом приборе при помощи коэффициента расхода прибора φ .