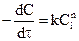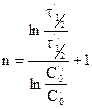Для расчета нормирующей константы используется уравнение

Нормальное (нормированное) уравнение прямой: описание, примеры, решение задач

В данной статье рассмотрим нормальное уравнение прямой на заданной плоскости. Получим нормальное уравнение, покажем не примере, дадим определение нормирующего множителя и разберем приведение общего уравнения к нормальному виду. Заключительной части посвятим основному приложению нормального уравнения прямой, то есть нахождение расстояние от точки до прямой на плоскости.

Нормальное уравнение прямой – описание и пример

Рассмотрим выведение нормального уравнения.

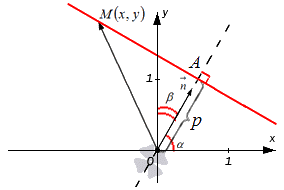
Фиксируем на плоскости систему координат О х у , где задаем прямую с точкой, через которую она проходит с нормальным вектором прямой. Нормальному вектору прямой дадим обозначение n → . Его начало обозначено точкой O . координатами являются cos α и cos β , углы которых расположены между вектором n → и положительными осями О x и O y . Это запишется так: n → = ( cos α , cos β ) . Прямая проходит через точку A с расстоянием равным p , где p ≥ 0 от начальной точки O при положительном направлении вектора n → . Если р = 0 , тогда A считается совпадающей с точкой координат. Отсюда имеем, что O A = p . Получаем уравнение, при помощи которого задается прямая.

Имеем, что точка с координатами M ( x , y ) расположена на прямой тогда и только тогда, когда числовая проекция вектора O M → по направлению вектора n → равняется p , значит при выполнении условия n p n → O M → = p .

O M → является радиус-вектором точки с координатами M ( x , y ) , значит O M → = ( x , y ) .

Применив определение скалярного произведения векторов, получим равенство вида: n → , O M → = n → · n p n → O M → = 1 · n p n → O M → = n p n → O M → = p

Тогда это же произведение будет иметь вид в координатной форме: n → , O M → = cos α · x + cos β · y

Отсюда cos α · x + cos β · y = p или cos α · x + cos β · y — p = 0 . Было выведено нормальное уравнение прямой.

Уравнение вида cos α · x + cos β · y — p = 0 называется нормальным уравнением прямой или нормированным уравнением прямой. Иначе говоря, уравнение прямой в нормальном виде.

Понятно, что такое уравнение представляет собой общее уравнение прямой A x + B y + C = 0 , где A и B имеют значения, при которых длина вектора n → = ( A , B ) равна 1 , а C является неотрицательным числом.

Теперь рассмотрим его геометрический смысл. Нормальное уравнение прямой вида cos α · x + cos β · y — p = 0 задает в системе координат О х у на плоскости прямую с наличием нормального вектора единичной длины n → = ( cos α , cos β ) , которая располагается на расстоянии равном p от начала координат по положительному направлению вектора n → .

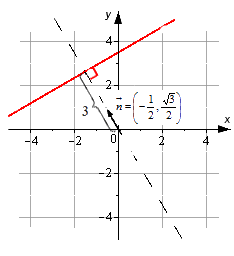
Если дано уравнение прямой вида — 1 2 · x + 3 2 · y — 3 = 0 , то на плоскости задается прямая, у которой нормальный вектор с координатами — 1 2 , 3 2 . Удаление прямой от начала координат идет по направлению, совпадающему с направлением нормального вектора n → = — 1 2 , 3 2 .

Приведение общего уравнения прямой к нормальному виду

Часто решение задач подразумевает использование нормального уравнения прямой, но само оно не дается в нормальном виде, поэтому необходимо для начала приводить к нормальному виду, после чего выполнять необходимые вычисления.

Нормальное уравнение получают из общего уравнения прямой. Когда на плоскости задается другим уравнением, то необходимо привести его к общему виду, после чего возможно приведение к нормальному. Если рассмотреть на примере, то это будет выглядеть так.

Для приведения общего уравнения прямой A x + B x + C = 0 к нормальному необходимо обе части умножить на нормирующий множитель, который имеет значение ± 1 A 2 + B 2 . Его знак определяется при помощи противоположности знака слагаемого C . При С = 0 знак выбирается произвольно.

Привести уравнение прямой 3 x — 4 y — 16 = 0 к нормальному виду.

Из общего уравнения видно, что А = 3 , В = — 4 , С = — 16 . Так как значение C отрицательное, необходимо брать положительный знак для формулы. Перейдем к вычислению нормирующего множителя:

1 A 2 + B 2 = 1 3 2 + ( — 4 ) 2 = 1 5

Теперь необходимо умножить обе части уравнения на одну пятую. Получим, что 1 5 · ( 3 x — 4 y — 16 ) = 0 ⇔ 3 5 · x — 4 5 · y — 16 5 = 0 .

Нормальное уравнение по заданной прямой найдено.

Ответ: 3 5 · x — 4 5 · y — 16 5 = 0 .

Определение состава и константы нестойкости одноядерного комплекса потенциометрическим методом

Пусть в результате реакции комплексообразования

Ме n + + pX — B =MeX_p n — pB (1)

образуется одноядерный комплекс. Согласно закону действия масс константа нестойкости

Чтобы вычислить константу, нужно экспериментальным путем определить концентрации всех частиц, участвующих в равновесии (1). Пусть к небольшому начальному количеству металло-ионов [Me n + ]_нач. прибавлен избыток адденда [X B — ]. За счет реакции (1) все ионы металла должны связаться в комплекс. С другой стороны, благодаря тому, что комплекс диссоциирует, в растворе создается определенная равновесная концентрация метало-ионов [Me n + ]. Убыль концентрации метало-ионов численно равна концентрации образовавшегося комплекса

так как согласно (1) один ион металла образует одну комплексную частицу.

Аналогично рассуждая и учитывая, что каждый металло-ион присоединяет p частиц адденда можно написать

[X B — ] — p[Me n + ] = [X B — ] (4)

Если комплекс прочен и в раствор введен избыток адденда, подавляющего диссоциацию, равновесная концентрация метало-ионов пренебрежимо мала по сравнению с начальными концентрациями. При этом условии (3) и (4) запишутся так:

Подставляя которые в (2) получим

К=[Me n + ][X B — ] р _нач. / [Me n + ]_нач. (5)

Логарифмирование (5) приводит к выражению

В координатах lg[Me n + ] _нач / [Me n + ]-lg[X B — ] это уравнение прямой, не проходящей через начало координат (рис.1). Угловой коэффициент прямой tgα=a/b=p. Поэтому, определив из графика tgα, находим число частиц адденда, входящих в комплекс.

Отрезок, отсекаемый на оси ординат при [X B — ]=1,численно равен логарифму константы нестойкости. Однако найденная таким образом константа, отвечает лишь одной концентрации X B — . При других концентрациях величина константы будет несколько отлична. Поэтому на практике константу определяют не из графика, а рассчитывают по уравнению (6) для ряда концентраций X B — и полученные результаты усредняют. Эта часть работы выполняется после того, как установлен состав комплекса.

Если начальные концентрации иона металла и адденда известны (они задаются самим исследователем), то для расчетов по формуле (6) нужно каким-то образом найти равновесную концентрацию иона металла. Для этой цели часто используется потенциометрия. Метод основан на измерении потенциала электрода, обратимого по отношению к ионам металла.

Потенциал электрода однозначно определяется концентрацией (точнее активностью) металло-ионов в растворе и выражается формулой Нернста

Таким образом, задача сводится к измерению равновесного потенциала электрода и вычислению [Me n + ], величина которой подставляется в (6).

Существует несколько приемов использования потенциометрии для исследования комплексных соединений.

В одном случае составляют цепь

Me│Me n + ║Me n + +X B — │Me

состоящую из двух одинаковых электродов, но один из них погружен в раствор с постоянной и известной концентрацией ионов изучаемого металла с₁,а второй – в раствор с такой же начальной концентрацией металло-ионов, но содержащий определенное количество адденда X B — . В последнем растворе за счет комплексообразования концентрация металло-иона уменьшается; она равна с₂. ЭДС такой цепи

где lg(с_1/с₂) и lg[Me n + ]_нач /[Me n + ] в выражении (7) представляет собой одну и ту же величину.

Вместо составления концентрационной цепи (8) можно составить две, в которых потенциал каждого электрода в отдельности измеряется по отношению к каломельному электроду сравнения, т.е.произвести раздельное определение величин Е₁ и Е₂ и отвечающих им [Me n + ]_нач и [Me n + ]

Mетоды исследования процессов комплексообразования в случае существования нескольких различных по составу частиц (с различным координационным числом) постоянно совершенствовались различными авторами не столько по методике измерений, сколько по способам обработки экспериментальных результатов. Рассмотрим некоторые из известных методов расчета общих констант прочности комплексов.

Методы расчета констант нестойкос т и комплексных соединений по данным потенциометрических измерений.

Метод Б ь е р р у м а

Теоретические положения, лежащие в основе современных ме­тодов математической обработки результатов потенциометрических измерений, были разработаны Я. Бьеррумом и связаны с развитыми им представлениями о ступенчатом комплексообразовании в раство­рах. Согласно этим представлениям равновесия в растворах ком­плексных соединений могут быть описаны следующими уравнениями:

Через Me обозначен ион металла-комплексообразователя, через L — лиганд, без указания их зарядов. Рассматривая их процессы в водных растворах, подразумевается гидратированность всех частиц. MeL_n — координационно-насыщенный комплекс в данной си­стеме. В дальнейших рассуждениях предполагается отсутствие многоядерных комплексов.

Константы равновесия каждой отдельной реакции представляют собой последовательные константы устойчивости или, по Бьерруму, константы образования (величины, обратные константам нестойкости). Приведем здесь все обозначения, которых мы будем придерживаться в дальнейшем. Некоторые из них уже упоминались.

К_n — общая константа нестойкости координационно-насыщенного комплекса MeL_n;

К_m — тоже для любого из промежуточных комплексов MeL_m;

k — последовательная константа нестойкости комплекса;

β_n — общая константа устойчивости координационно-насыщен­ного комплекса.

(11)

β_i— общая константа устойчивости промежуточного комплекса

x— последовательная константа устойчивости

(12)

С_м— начальная концентрация ионов металла-комплексообразователя или общая концентрация всех частиц, содержащих в том или ином виде металл — комплексообразователь;

[Me] — равновесная концентрация ионов металла;

С_L— общая концентрация лиганда;

[L] — равновесная концентрация лиганда;

[MeL_n], [MeL_i,] — равновесные концентрации комплексов;

Константы устойчивости выражаются следующими уравнениями;

(13)

(14)

(15)

(15а)

Бьеррум ввел понятие о функции образования

(16)

Функцию образования можно определить как отношение концентрации лиганда, связанного в комплекс, к общей соли металла.

Эта функция может быть выражена через константы устойчивости. Числитель правой части уравнения (17) по определению равен:

Используя уравнение (15), запишем:

Знаменатель этой же части уравнения (16) можно выразить следующим образом:

Подставляя эти выражения в уравнение (16), получим:

(21)

Для решения полученного уравнения (вернее системы уравнений этого типа) можно использовать следующий метод, предложенный Бьеррумом.

Если из экспериментальных данных определяются значения равновесных концентраций лиганда, то по уравнению (16) можно вычислить функцию образования, поскольку остальные величины, входящие в него, также известны из опыта. Далее строится график, выражающий зависимость от lg[L]. По этой кривой можно, прежде всего, определить максимальное число координированных групп п. Достигнув максимального значения, не изменяется с увеличением концентрации лиганда.

Вид кривой образования показан на рис. 1.

Для определения констант устойчивости находят значения lg [L] при . В первом приближении предполагается, что при этом условии в растворе присутствуют в равных концентрациях два комплекса MeL_j и MeL_j-1.

Из уравнения (13) следует, что в данной точке значение lg[L] будет соответствовать lgх_j

Таким образом, константа устойчивости комплекса MeL х₁ =β₁ будет равна концентрации лиганда при п = 1/2. Последовательной константе устойчивости отвечающий присоединению к MeL одной группы L, будет соответствовать значение концентрации лиганда при =1,5 и т. д.

Рис. 1. Кривая образования

Такое предположение будет тем ближе к истине, чем больше отличаются между собой последовательные константы устойчивости, т. е. чем больше область концентраций лиганда в которой преоб­ладает каждый комплекс. Уточнение результатов можно произвести путем последовательных приближений с помощью уравнения (21).

Возможны и другие способы решения уравнения (21), которые иногда представляют в следующем виде:

+ ( — 1) β₁[L] + ( — 2) β₂[L] 2 + . ( — п) β_n [L] n = 0. (22)

Ряд методов решения его, относящихся к частному случаю, когда максимальное число координированных групп равно 2, рассмотрены Ирвингом и Россоти. В работе этих авторов указываются ограничения каждого варианта в зависимости от соотношения между последовательными константами устойчивости.

Метод Бьеррума как в его первоначальном виде, так и видоизмененном, чаще всего применяется для обработки данных рН-метрических измерений. Равновесную концентрацию лиганда и функцию образования в этом случае выражают через концентрацию водородных ионов.

В некоторых случаях метод расчета по Бьерруму используется также для вычисления констант диссоциации кислот или оснований, участвующих в комплексообразовании. При этих расчетах рассматривают водородный ион как лиганд, анион кислоты как центральный ион, и определяют функцию образования.

Для определения констант диссоциации кислоты решается си­стема уравнений, выражающих зависимость от pH.

Для вычисления констант устойчивости по данным экспериментальных методов, определяющих равновесную концентрацию ионов металла-комплексообразователя, привлекаются другие способы расчета. На примере этих данных разработан метод Ледена.

Этот метод основан на использовании функции F, представляющей собой отношение общей концентрации всех комплексов, имеющихся в системе, к равновесной концентрации ионов металла-комплексообразователя.

(23)

К.Б. Яцимирский предложил назвать эту функцию «закомплексованностью» (строго говоря, это название относится к близкой к ней функции ).

Общая концентрация соли металла складывается из концентраций свободных-ионов металла и всех комплексных частиц (уравнение 19)

Общая концентрация лиганда выражается уравнением (17):

Уравнение (19) и (17) можно представить в следующем виде:

Из уравнения (23) находится функция F

(26)

Разделив обе части уравнения на [L], имеем:

(27)

Значения С_м и [Me] известны из опыта. Для вычисления равновес­ной концентрации лиганда [L] Леден предлагает использовать среднее координационное число N.

В отличие от функции образования число N представляет собой отношение концентрации лиганда, связанного в комплекс, к общей концентрации комплексов. Другими словами, N является средним числом координированных групп, связанных с комплексообразователем.

(28)

Или, учитывая уравнения (17) и (19):

(29)

В первом приближении можно рассматривать N как постоянную величину в некотором узком интервале концентраций лиганда. При исследовании комплексных соединений потенциометрическим мето­дом, использующим металлические или амальгамные электроды, приближенное значение N можно определить по разности потенциалов индикаторного электрода при двух различных концентрациях лиганда:

Если общая концентрация соли металла в обоих опытах постоян­на, то последнее уравнение запишется в следующем виде:

(30)

Принимая, в первом приближении, равновесные концентрации лигандов равным общим концентрациям, вычислим N.

(31)

Зная N, можно определить равновесную концентрацию лиганда (пока, конечно, приближенно).

(32)

Далее задача сводится к вычислению F(L) no уравнению (27) и построению графика в координатах F(L)–[L]. Экстраполяция полу­ченной прямой до [L]=0 позволяет определить значение β₁, соот­ветствующее ординате точки пересечения данной прямой с осью ординат.

Для определения β₂ вычисляется . Полученные значения откладываются на графике как функции [L]. Теперь экстраполя­ция до [L]=0 дает β₂. Подобным же образом продолжается расчет β₃ . и β_n.

Найденные значения β_iявляются приближенными. Для лучших результатов рассчитывают новые значения из уравне­ния (29).

Далее, по уравнению (32) вычисляются новые значения, и повто­ряется весь расчет β_i.

Такие приближенные расчеты продолжаются до тех пор, пока не будут достигнуты постоянные значения β_i.

Метод Ледена требует очень точных экспериментальных данных и недостаточно надежен при определении значений β_i (если i > 2).

Близко к этим методам примыкает вариант расчета констант нестойкости при ступенчатом комплексообразовании, предложенный К. Б. Яцимирским.

M е т о д К.Б. Я ц и м и р с к о г о

Метод Яцимирского состоит в построении графика, выражаю­щего зависимость логарифма равновесной концентрации иона-комплексообразователя или пропорциональной ему величины от лога­рифма равновесной концентрации лиганда. Первоначально этот метод был предложен для вычисления констант нестойкости ком­плексов по данным полярографии. Затем автор метода распространил его и на другие экспериментальные методы (потенциометрический, метод растворимости).

К. Б. Яцимирский исходит из предположения о том, что в дан­ных условиях в растворе имеются два комплекса MeL_m и MeL_m+1. Суммарная концентрация комплексных частиц в растворе выражается
следующим уравнением:

(33)

Уравнение (33) справедливо для прочных комплексов, когда концентрацией свободных ионов металла можно пренебречь, как слагаемым.

Это уравнение можно записать в следующем виде:

(34)

k_m+1— последовательная константа нестойкости, соответствующая процессу:

Если экспериментальное исследование комплексных соединений проводится потенциометрическим методом с металлическими или амальгамными электродами, то измеряемое значение ЭДС будет величиной, пропорциональной равновесной концентрации свободных ионов металла в растворе комплексных соединений.

Не учитывая коэффициентовактивностей ионов, мы можем представить уравнение э.д.с. концентрационной цепи в виде:

(35)

где Е_х потенциал электрода в растворе комплексных соединений, Е₀ – тоже в растворе простой соли при начальной концентрации ионов металла С_м.

Прологарифмируем уравнение (34) и, решив его относительно подставим его значение в уравнение (35).

(36)

Уравнение (36) показывает, что зависимость потенциала электрода от логарифма концентрации лиганда при ступенчатом комплексообразовании выражается кривой, выпуклой к оси концентраций (рис. 2)

Рис. 2. Зависимость потенциала ртутного электрода от логарифма равновесной концентрации сульфит-ионов.

Решением уравнения (36) можно найти значения последователь­ных констант нестойкости.

Дифференцирование его по dlg[L] приводит к следующему урав­нению:

(37)

В той точке кривой, где K_m+1 численно равна [L], тангенс угла касательной выразится cледующим образом:

(38)

При этом условии концентрации обеих форм комплексов равны между собой.

Таким образом, если к кривой, построенной по эксперименталь­ным значениям Е_х и lg[L], провести касательную с угловым коэф­фициентом , то абсцисса точки касания определит логарифм последовательной константы нестойкости k_m+1.

Проведением нескольких касательных с тангенсами угла наклона: ; можно определить значение всех ступенчатых констант нестойкости в данной системе.

На рис. 2 в качестве примера показана зависимость потенциала ртутного электрода в растворе сульфитных комплексов ртути от логарифма равновесной концентрации сульфит-ионов. Можно видеть, что прямые с угловыми коэффициентами 0,072 (2,5∙0,029) и 0,094(3,5·0,029) являются касательными в точках, абсциссы кото­рых равны соответственно —0,26 и —0,16. Отсюда последователь­ные константы нестойкости комплексов с тремя и четырьмя коорди­нированными группами будут равны:

Для вычисления общей константы нестойкости используется уравнение (34). В точке, где k_m+1 = [L], оно преобразуется в сле­дующее:

(39)

. (40)

По уравнению (36) можно найти ряд параллельных значений lgK_m, если использовать серию экспериментальных данных для и lg[L] (А) и учесть последовательную константу нестойкости k_m+1

. (41)

Метод Яцимирского отличается большой наглядностью и просто­той расчета. Если область существования одного из комплексов достаточно широка, то зависимость Е от lg[L] приближается к пря­молинейной. В этом случае угловой коэффициент прямой (tgα) равен . Отсюда легко определяется число координированных групп

. (42)

Уравнение (41) примет вид:

. (43)

Чаще всего прямолинейная зависимость имеет место при высокой концентрации лиганда и характеризует преобладание координац­ионно насыщенного комплекса. Можно считать, что данный ком­плекс преобладает практически полностью, если доля его в растворе превышает 90%. Под «долей данного комплекса» понимается отно­шение его концентрации к общей концентрации соли металла.

. (44)

К.Б. Яцимирский показал, что максимальное накопление данного комплекса определяется отношением ступенчатых констант нестойкости

. (45)

Из уравнения (45) следует, что для того, чтобы максимальная доля данного комплекса превышала 90%,соотношение между последовательными константами нестойкости должно составлять по крайней мере 2∙10 3 .Если в системе образуется больше двух комплексов с мало отличающимися друг от друга последовательными константами не­стойкости, то доля комплекса еще больше понижается. Предполо­жение о существовании в этих условиях только двух комплексов уже не будет справедливо. Наряду с рассматриваемыми формами, в растворе будут представлены в большем или меньшем количестве и другие виды комплексов. Естественно, что в данном случае метод Яцимирского, также как и другие методы, дает только приближен­ные значения констант нестойкости. При последующем расчете они могут быть учтены. Одновременно с этими вычислениями можно уточнить значения равновесных концентраций лиганда, которые в первом приближении принимаются равными общим концентрациям его. Для этой цели можно воспользоваться ходом рассуждений Ледена, касающимся определения среднего координационного числа.

Выше уже указывалось, что объединение различных способов расчета может оказаться наиболее полезным для обработки экспе­риментальных данных при ступенчатом комплексообразовании.

Рассмотренные методы вычислений констант устойчивости свя­заны не только с потенциометрическими измерениями. Они могут быть использованы в других экспериментальных методах, опреде­ляющих равновесные концентрации частиц, участвующих в реакции комплексообразовани

Реакции n-го порядка

Как мы уже знаем, сложные реакции типа 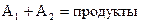могут протекать по n-му порядку, при этом n может быть целым или дробным числом. Скорость реакции n-го порядка при равных начальных концентрациях реагирующих веществ выражается уравнением:

Разделив переменные, получаем:

.

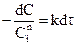
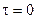
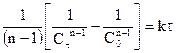
Интегрируя данное выражение в пределах от до τ, и от С₀ до С_τ, получаем

.

Данное уравнение можно представить относительно С_τ, что позволяет рассчитать концентрацию реагента в любой момент времени, если известны k и n:

.

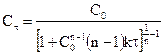
Уравнение для времени половинного превращения можно получить, как и ранее, приняв, что :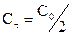

.

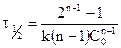
Представленные уравнения можно использовать для реакций n-го порядка (кроме первого!).

n	Кинетическое уравнение	Вид зависимости	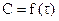Уравнения для расчета
k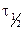

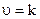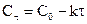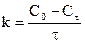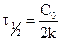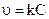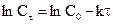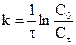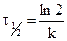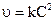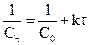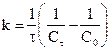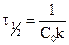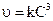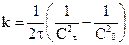определение порядка реакции

Для определения порядка реакции используются различные методы.

Метод подстановки (аналитический): заключается в подстановке экспериментальных данных в уравнения кинетики реакции нулевого, первого, второго и третьего порядков и определении, которое из этих уравнений приводит к постоянному значению константы скорости реакции (можно считать, что уравнение описывает процесс, если рассчитанные по нему значения констант колеблются около какой-то средней величины и отклонения от среднего лежат в пределах возможных погрешностей определения). Если ни одно из уравнений не дает такого результата, то реакция является сложной.

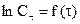
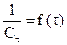
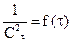
Графический метод: заключается в построении графика, выражающего зависимость различных функций концентрации от времени, и определении, для которой из них зависимость выражается прямой линией. Так для реакции первого порядка прямая получается в системе координат ; для реакции второго порядка ; для реакции третьего порядка . По тангенсу угла наклона прямой можно определить константу скорости реакции. Для реакции нулевого порядка зависимость концентрации от времени дает прямые, параллельные оси абсцисс.

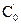
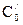
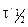
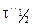
Метод определения периода полураспада: основан на определении промежутка времени, в течение которого концентрации (или количества) исходных веществ уменьшаются ровно в два раза. Проводя реакцию при двух различных начальных концентрациях и и определяя для обоих случаев периоды полураспада и можно определить порядок реакции.

Вспомним уравнение для периода полураспада реакции n-го порядка:

.

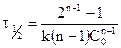
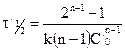
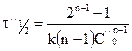
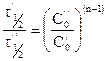
Получим и , разделив одно уравнение на другое, получим:

.

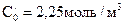
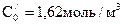
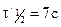
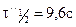
Например, и ; периоды полураспада и . Определить порядок реакции (n=1,96≈2).

Метод изоляции или метод избытка: реагентов заключается в том, что проводят серии опытов, в каждом из которых изучается влияние изменения концентрации только одного из исходных веществ на скорость реакции. это достигается применением всех остальных исходных веществ в данной серии опытов в таком избытке, что расход их в ходе реакции существенно не меняет их количества (концентрации), которые поэтому можно считать постоянными. Охватывая, таким образом, все исходные вещества, можно установить влияние изменения концентрации каждого из них на скорость реакции и отсюда определить порядок реакции и уравнение кинетики.

Рассмотреть самостоятельно – дифференциальный метод (разновидность графического метода?)!

Кинетика сложных реакций, состоящих из двух или большего числа простых реакций, в той или иной форме связанных между собой, зависит от формы связи между этими реакциями и от соотношения их скоростей. Типичными по форме такой связи являются реакции:

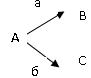
Параллельные: две реакции называются параллельными, если в обеих в качестве исходного вещества выступает одно и то же вещество, т.е. это реакции вида:

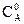
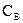
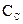
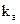
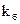
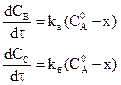
Обозначим, через начальную концентрацию вещества А, через х – изменение его концентрации к моменту времени τ, через и концентрации образовавшихся веществ и через и константы скоростей соответствующих реакций. Тогда для скорости образования продуктов реакции имеем:

(*)

Сумма этих скоростей определяет скорость расходования исходных веществ:

.

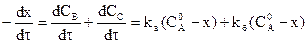
С другой стороны, отношение этих двух уравнений (*) дает:

.

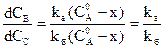
Таким образом, если в данных условиях термодинамически возможны два или три направления химический реакции, то преобладание того или другого из них и относительные количества получаемых продуктов реакции определяются всецело соотношением скоростей этих реакций, а не соотношением термодинамической устойчивости конечных продуктов. Если реакции значительно различаются по скорости, то обычно реакцию, обладающую большей скоростью, называют главной (основной), а остальные – побочными. При не слишком большом различии в скоростях главной реакцией называют реакцию, приводящую к получению основного нужного продукта, хотя бы она и обладала меньшей скоростью.

Последовательные (или консекутивные): две реакции называются последовательными, если вещество, образующееся в одной стадии, является исходным для другой, т.е. это реакции вида:

,

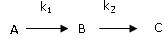
где В промежуточный продукт в процессе получения вещества С; k₁ и k₂ — константы скоростей двух стадий превращения.

Данная схема представляет собой простейшую последовательную реакцию, которая происходит в две ступени, и каждая из этих ступеней является простой мономолекулярной реакцией. В общем же случае ступеней может быть больше, а стадии могут не быть мономолекулярными.

Расчет кинетики последовательных реакций очень сложен. Отметим только, что если одна из ступеней обладает значительно меньшей скоростью, чем остальные, то общая скорость реакции определяется скоростью именно этой реакции.

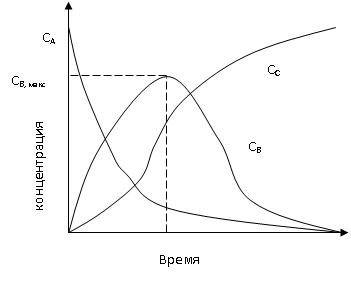
Зависимость концентрации веществ, участников реакции, от времени можно рассмотреть на примере простейшей последовательной реакции:

Из данных графических зависимостей следует, что в начале процесса, когда концентрация вещества А еще сравнительно высока, скорость первой реакции значительна и увеличение концентрации В происходит быстро. По мере израсходования вещества А уменьшается и скорость образования вещества В. Это приводит к тому, что расход вещества В на образование вещества С, начиная с какого-то момента времени, уже не компенсируется в полном степени образованием его из вещества А и концентрация вещества В в системе начинает уменьшаться. Вследствие этого кривая Св проходит через максимум. Положение таких кривых для различных последовательных реакций неодинаково, т.к. оно зависит от соотношения в скоростях этих реакций, но общий характер зависимости остается обычно таким, как он рассмотрен нами.

Кривые на рисунке описываются уравнениями:

,

,

.

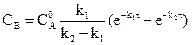
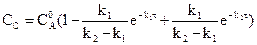
(реакции первого порядка)

Было доказано, что максимальная концентрация промежуточного продукта В, достигаемая в ходе реакции, не зависит от абсолютных значений констант скоростей k₁ и k₂, а зависит только от их отношения 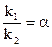, т.е. чем больше значение α, тем больше должна быть концентрация Св, макс.

При k₁ > k₂ скорость образования промежуточного продукта будет значительно выше скорости его расходования. Таким образом, если промежуточный продукт является целевым и необходимо увеличить его выход, то это может быть достигнуто увеличением k₁, что можно достигнуть введением в реакционную систему селективного катализатора, который увеличил бы скорость первой стадии при неизменной скорости второй. Если зависимость скоростей стадий от температуры различна, то тот же эффект может быть достигнут изменением температуры.

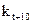
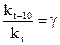
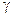
При k₁ 0 С и через константу скорости той же реакции при температуре (t+10) 0 С. Отношение называется температурным коэффициентом скорости. Было предложено приближенное правило, согласно которому повышение температуры на 10 0 С увеличивает скорости реакций примерно в 2-4 раза (правило Вант-Гоффа), т.о. можно принять равным примерно 2-4.

Данное правило определяет только порядок изменения скорости, присущий значительной части различных химических реакций при обычных температурах. Однако для ориентировочной оценки возможного влияния температуры оно нередко бывает полезным, в особенности при отсутствии данных для более точного расчета.