Решение систем дифференциальных уравнений с помощью характеристического уравнения
Пусть дана однородная система
где 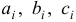
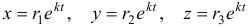
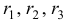
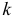
называется характеристическим уравнением системы. Отыскав корни этого уравнения, и поочередно подставляя их в исходную систему, определим коэффициенты 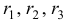
Пример №1
Найти общее решение системы
Решение:
Система в данном случае имеет вид:
Характеристическое уравнение 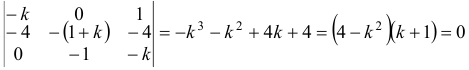
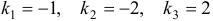
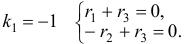
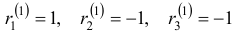
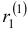
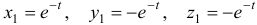
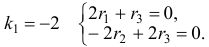
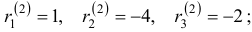
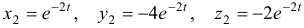
Наконец, для 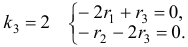
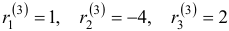
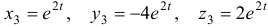
Общее решение данной системы дифференциальных уравнений таково:
Пример №2
Решение:
Чаще системы дифференциальных уравнений записывают в виде: 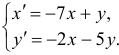
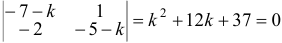
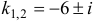
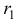
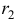
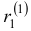
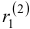
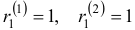
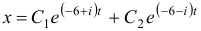
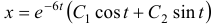
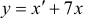
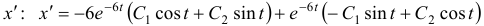
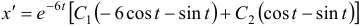
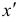
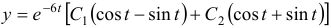
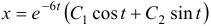
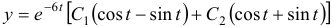
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Возможно вам будут полезны эти страницы:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Для системы характеристическое уравнение имеет вид
Характеристическое уравнение составляется для цепи после коммутации. Оно может быть получено следующими способами:
- непосредственно на основе дифференциального уравнения вида (2) (см. лекцию №24), т.е. путем исключения из системы уравнений, описывающих электромагнитное состояние цепи на основании первого и второго законов Кирхгофа, всех неизвестных величин, кроме одной, относительно которой и записывается уравнение (2);
- путем использования выражения для входного сопротивления цепи на синусоидальном токе;
- на основе выражения главного определителя.
Согласно первому способу в предыдущей лекции было получено дифференциальное уравнение относительно напряжения 
Следует отметить, что, поскольку линейная цепь охвачена единым переходным процессом, корни характеристического уравнения являются общими для всех свободных составляющих напряжений и токов ветвей схемы, параметры которых входят в характеристическое уравнение. Поэтому по первому способу составления характеристического уравнения в качестве переменной, относительно которой оно записывается, может быть выбрана любая.
Применение второго и третьего способов составления характеристического уравнения рассмотрим на примере цепи рис. 1.
Составление характеристического уравнения по методу входного сопротивления заключается в следующем:
записывается входное сопротивление цепи на переменном токе;
j w заменяется на оператор р;
полученное выражение 
совпадает с характеристическим.
Следует подчеркнуть, что входное сопротивление может быть записано относительно места разрыва любой ветви схемы. При этом активный двухполюсник заменяется пассивным по аналогии с методом эквивалентного генератора. Данный способ составления характеристического уравнения предполагает отсутствие в схеме магнитосвязанных ветвей; при наличии таковых необходимо осуществить их предварительное развязывание.
Для цепи на рис. 1 относительно зажимов источника

Заменив j w на р и приравняв полученное выражение к нулю, запишем
 . . | (1) |
При составлении характеристического уравнения на основе выражения главного определителя число алгебраических уравнений, на базе которых он записывается, равно числу неизвестных свободных составляющих токов. Алгебраизация исходной системы интегро-дифференциальных уравнений, составленных, например, на основании законов Кирхгофа или по методу контурных токов, осуществляется заменой символов дифференцирования и интегрирования соответственно на умножение и деление на оператор р. Характеристическое уравнение получается путем приравнивания записанного определителя к нулю. Поскольку выражение для главного определителя не зависит от правых частей системы неоднородных уравнений, его составление можно производить на основе системы уравнений, записанных для полных токов.
Для цепи на рис. 1 алгебраизованная система уравнений на основе метода контурных токов имеет вид
Отсюда выражение для главного определителя этой системы

Приравняв D к нулю, получим результат, аналогичный (1).
Общая методика расчета переходных процессов классическим методом
В общем случае методика расчета переходных процессов классическим методом включает следующие этапы:
- Запись выражения для искомой переменной в виде
.
(2) - Нахождение принужденной составляющей общего решения на основании расчета установившегося режима послекоммутационной цепи.
- Составление характеристического уравнения и определение его корней (для цепей, описываемых дифференциальными уравнениями первого порядка, вместо корней можно находить постоянную времени t — см. лекцию №26). Запись выражения свободной составляющей в форме, определяемой типом найденных корней.
- Подстановка полученных выражений принужденной и свободной составляющих в соотношение (2).
- Определение начальных условий и на их основе – постоянных интегрирования.
Примеры расчета переходных процессов классическим методом
1. Переходные процессы в R-L цепи при ее подключении к источнику напряжения
Такие процессы имеют место, например, при подключении к источнику питания электромагнитов, трансформаторов, электрических двигателей и т.п.
Рассмотрим два случая:
а)
б) 
Согласно рассмотренной методике для тока в цепи на рис. 2 можно записать
 . . | (3) |
Тогда для первого случая принужденная составляющая тока
 . . | (4) |

откуда 

 . . | (5) |
Подставляя (4) и (5) в соотношение (3), запишем

В соответствии с первым законом коммутации 

откуда 
Таким образом, ток в цепи в переходном процессе описывается уравнением

а напряжение на катушке индуктивности – выражением

Качественный вид кривых 

При втором типе источника принужденная составляющая рассчитывается с использованием символического метода:

где 

Выражение свободной составляющей не зависит от типа источника напряжения. Следовательно,

Поскольку 

Таким образом, окончательно получаем
 . . | (6) |
Анализ полученного выражения (6) показывает:
- При начальной фазе напряжения
постоянная интегрирования А=0. Таким образом, в этом случае коммутация не повлечет за собой переходного процесса, и в цепи сразу возникнет установившийся режим.
- При
свободная составляющая максимальна по модулю. В этом случае ток переходного процесса достигает своей наибольшей величины.
Если 





Таким образом, для линейной цепи максимальное значение тока переходного режима не может превышать удвоенной амплитуды принужденного тока: 
Аналогично для линейной цепи с конденсатором: если в момент коммутации принужденное напряжение равно своему амплитудному значению и постоянная времени 


2. Переходные процессы при отключении катушки индуктивности от источника питания
При размыкании ключа в цепи на рис. 5 принужденная составляющая тока через катушку индуктивности 

откуда 

В соответствии с первым законом коммутации

Таким образом, выражение для тока в переходном режиме
и напряжение на катушке индуктивности
 . . | (7) |
Анализ (7) показывает, что при размыкании цепей, содержащих индуктивные элементы, могут возникать большие перенапряжения, которые без принятия специальных мер могут вывести аппаратуру из строя. Действительно, при 

3. Заряд и разряд конденсатора
При переводе ключа в положение 1 (см. рис. 6) начинается процесс заряда конденсатора:

Принужденная составляющая напряжения на конденсаторе 
Из характеристического уравнения
определяется корень 


При t=0 напряжение на конденсаторе равно 



Соответственно для зарядного тока можно записать

В зависимости от величины 




При разряде конденсатора на резистор 


Тогда, принимая, что к моменту коммутации конденсатор был заряжен до напряжения 


Соответственно разрядный ток
 . . | (8) |
Как видно из (8), во избежание значительных бросков разрядного тока величина 
В заключение отметим, что процессы заряда и разряда конденсатора используются в генераторах пилообразного напряжения, широко применяемых в автоматике. Для этого ключ в схеме на рис. 6 заменяется на электронный.
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
- Составить характеристическое уравнение для цепи на рис. 1, используя выражение входного сопротивления относительно места разрыва ветви с резистором
.
- Может ли в одной части линейной цепи протекать колебательный переходный процесс, а в другой – апериодический?
- Для чего в схеме на рис. 5 служит цепочка, состоящая из диода и резистора R?
- Почему можно разрывать ветвь с конденсатором и нельзя – ветвь с индуктивным элементом?
- Почему корни характеристического уравнения не зависят от того, относительно какой переменной было записано дифференциальное уравнение?
- Для цепи на рис. 8 составить характеристическое уравнение и определить, при каких значениях
переходный процесс в ней будет носить апериодический характер, если
.
Ответ: 
Определить 




Ответ: 
Для системы характеристическое уравнение имеет вид
Дифференциальное уравнение y´+3xy=
является __________(каким?) дифференциальным уравнением первого порядка (вставить слово)
Общее решение линейного дифференциального уравнения
y´´+4y=0 имеет вид
Система дифференциальных уравнений
эквивалентна уравнению вида
Система дифференциальных уравнений
эквивалентна уравнению вида
В связи с дифференциальными уравнениями рассматривают ___ решения
В связи с дифференциальными уравнениями рассматривают ____ решения
График любого решения дифференциального уравнения называют______ (завершите определение словосочетанием)
Дано линейное однородное дифференциальное уравнение y´´–4y´+4y=0 Его общим решением является функция
Дано линейное однородное дифференциальное уравнение y´´–6y´+5y=0, тогда его общее решение имеет вид
Даны уравнения и . Укажите верные для них утверждения
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение
Дифференциальное уравнение является
Дифференциальное уравнение
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение является
Дифференциальное уравнение x2y´=x2+y2 является уравнением
Дифференциальное уравнение x3y´+x2y+2=0 является
Дифференциальное уравнение y´+xy=x3y2 является уравнением ___________ (укажите название)
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид:
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения = 0 характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Завершите условие Уравнение вида будет однородным в том и только том случае, когда и являются однородными функциями _________ ( слово) порядка
Интегральная кривая дифференциального уравнения – это
Корни характеристическое уравнение есть
Нахождение функции , определенной на некотором интервале , имеющей на производную , такую, что для всех и удовлетворяющей условию , где и в точке определена функция , называется задачей
Общее решение дифференциального уравнения в областибудет функция
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения xy´´=y´ имеет вид
Общее решение линейного неоднородного дифференциального уравнения имеет вид
Общее решение линейного однородного дифференциального уравнения y´´–16y=0 имеет вид
Общее решение уравнения y´=e–2x имеет вид
Общее решение уравнения y´´+y=x+2 имеет вид
Общее решение уравнения y´´–y´=ex имеет вид
Общий интеграл дифференциального уравнения имеет вид
Общим решением линейного дифференциального уравнения y´´+9y=0 является функция
Общим решением системы дифференциальных уравнений , является
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Порядок дифференциального уравнения – это неизвестной функции
При нахождении общего решения неоднородной системы линейных дифференциальных уравнений -го порядка используют
При решении линейных дифференциальных уравнений с постоянными коэффициентами используют
Рассмотрим уравнение Для этого уравнения верно:
Рассмотрим уравнение Для этого уравнения верно:
Рассмотрим уравнение Для этого уравнения верно:
Рассмотрим уравнение Для этого уравнения верно:
Рассмотрим уравнение Для этого уравнения верно:
Решение дифференциального уравнения второго порядка можно свести к решению дифференциального уравнения первого порядка в двух случаях Выберите их
Решить дифференциальное уравнение – это значит найти
Семейству линий сопоставьте огибающую
Семейству линий сопоставьте огибающую
Семейству линий сопоставьте огибающую
Теорема существования и единственности решения задачи Коши для дифференциального уравнения выполнена в области
Теорема существования и единственности решения задачи Коши для дифференциального уравнения выполнена в области
Теорема существования и единственности решения задачи Коши для дифференциального уравнения выполнена в области
Теорема существования и единственности решения задачи Коши для дифференциального уравнения выполняется в области
Теорема существования и единственности решения задачи Коши для дифференциального уравнения выполняется в области
Теорема существования и единственности решения задачи Коши для дифференциального уравнения выполнена в области
Теорема существования и единственности решения задачи Коши для дифференциального уравнения выполнена в области
Укажите верные для уравнений Клеро и Лагранжа утверждения
Укажите соответствие между типом дифференциального уравнения второго порядка и методом его решения
Укажите соответствия между дифференциальными уравнениями и их характеристическими уравнениями
Укажите соответствия между дифференциальными уравнениями и их частными решениями
Укажите соответствия между дифференциальными уравнениями и корнями их характеристических уравнений
Укажите соответствия между функциями и дифференциальными уравнениями
Укажите соответствия между функциями и дифференциальными уравнениями
Укажите утверждения верные для дифференциального уравнения Лагранжа
Укажите утверждения, верные для дифференциального уравнения Клеро
Установить зависимость вида общего решения дифференциального уравнения от корней соответствующего характеристического уравнения
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальными уравнениями первого порядка и их названием
Установить соответствие между линейным однородным дифференциальным уравнением и видом его общего решения
Установить соответствие между линейным однородным дифференциальным уравнением и видом общего решения этого уравнения
Установить соответствие между линейным однородным дифференциальным уравнением и его характеристическим многочленом
Установить соответствие между линейными однородными дифференциальными уравнением и его общим решением
Установить соответствие между характеристическим многочленом и линейным однородным дифференциальным уравнением
Характеристическое уравнение дифференциального уравнения есть
Характеристическое уравнение дифференциального уравнения есть
Характеристическое уравнение дифференциального уравнения есть
Характеристическое уравнение дифференциального уравнения есть
Характеристическое уравнение дифференциального уравнения есть
Характеристическое уравнение дифференциального уравнения есть
Частное решение дифференциального уравнения есть
Частное решение дифференциального уравнения есть
Частное решение дифференциального уравнения есть
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение линейного неоднородного дифференциального уравнения второго порядка y´´+4y=ex имеет вид
Частное решение уравнения при есть
Частное решение уравнения при есть
http://toehelp.ru/theory/toe/lecture25/lecture25.html
http://antimuh.ru/files/details/1114355
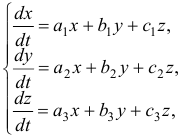
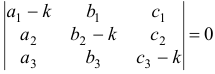

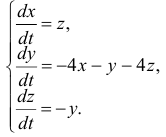
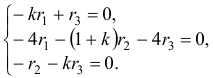
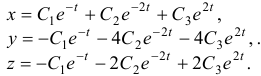
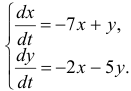





 .
.


 постоянная интегрирования А=0. Таким образом, в этом случае коммутация не повлечет за собой переходного процесса, и в цепи сразу возникнет установившийся режим.
постоянная интегрирования А=0. Таким образом, в этом случае коммутация не повлечет за собой переходного процесса, и в цепи сразу возникнет установившийся режим. свободная составляющая максимальна по модулю. В этом случае ток переходного процесса достигает своей наибольшей величины.
свободная составляющая максимальна по модулю. В этом случае ток переходного процесса достигает своей наибольшей величины.





 .
. переходный процесс в ней будет носить апериодический характер, если
переходный процесс в ней будет носить апериодический характер, если  .
.