Для уравнений какого типа справедлив принцип максимума

Лекция 8. Принцип максимума для гармонических функций

Среди свойств, которыми обладают гармонические функции, одно свойство, называемое принципом максимума, несомненно имеет ведущее значение.

Теорема. Если функция U=U(x,y) гармоническая в ограниченной области D и непрерывная в соответствующей замкнутой области то она не может внутри этой области принимать значения, большие чем максимум ее значений на границе Г, и меньшие, чем минимум ее значений на Г, то есть

Доказательство. Обозначим через m максимум значений U(x,y) на Г и предположим, что максимальное значение функции равно U(x_o,y_o)=M>m и принимается во внутренней точке (x_o , y_o) области D. Составим вспомогательную функцию

где d — диаметр области D (максимальное расстояние между любыми двумя точками, принадлежащими области). Из неравенства вытекает, что на Г

В то же время функция V(x,y) принимает свое максимальное значение в некоторой (внутренней) точке области D, причем

Как известно, в этой точке V_x = V_y = 0, а следовательно, Однако

Полученное противоречие означает, что предположение M > m неверно, и мы доказали, что внутри D

Для доказательства неравенства, ограничивающего U(x, y) снизу

достаточно применить уже полученный результат к функции — U(x, y), которая, очевидно, тоже является гармонической. Теорема о максимуме и минимуме доказана.

На самом деле, если гармоническая функция , то она не может принимать внутри области D значения, равные и, то есть

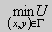
Это утверждение называется строгим принципом максимума (в отличие от предыдущего утверждения — «нестрогого» принципа максимума). Его доказательство сложнее, и мы доказывать это утверждение не будем. Сформулируем следствия из него.

Следствие 1. Если функция U=U(x, y) непрерывная в ограниченной замкнутой области и гармоническая в D, то

В частности, если , то U(x, y) ≡ 0 в D.

Это утверждение вытекает из (39):

Объединяя эти неравенства в систему, будем иметь:

Из принципа максимума следуют и многие другие важные свойства гармонических функций. Однако мы сейчас сформулируем и докажем лишь две теоремы.

Напомним постановку задачи Дирихле: в области D найти решение уравнения Лапласа, удовлетворяющее граничному условию U|_Г = f(s).

Теорема о единственности решения задачи Дирихле.

Решение задачи Дирихле для уравнения Лапласа в ограниченной области (если оно существует) единственное.

Доказательство. Пусть задача имеет два решения U=U₁(x, y) и U=U₂(x, y), удовлетворяющих одному и тому же условию Дирихле на границе Г. Тогда их разность V = U₁ — U₂ тоже будет непрерывной и гармонической функцией и на границе будет обращаться в нуль. По принципу максимума

Следовательно, V = U₁ — U₂ ≡ 0, то есть U₁(x, y) ≡ U₂(x, y). Единственность доказана. Вторая теорема имеет еще более длинное название.

Теорема о непрерывной зависимости решения задачи Дирихле от граничных условий.

Пусть U₁ и U₂ — две гармонические в области D функции, граничные значения которых равны, соответственно, f₁(s) и f₂(s), Если при некотором то всюду в рассматриваемой области D.

Доказательство. Рассмотрим функцию V = U₁ — U₂, удовлетворяющую уравнению Лапласа в области D и принимающую на границе Г значения f(s) = f₁(s)-f₂(s). На основании следствия 1 мы можем утверждать, что

что и требовалось доказать.

Эти теоремы имеют большое значение в вопросе о корректности задачи Дирихле, который мы рассмотрим в дальнейшем.

Отметим, что принцип максимума выполняется и для функций, гармонических в пространственных областях.

О принципе максимума для одного класса нелинейныхпараболических уравнений Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Коньков А.А.

В статье исследуются решения нелинейных параболических уравнений в полупространстве. Известно, что в случае линейных уравнений для справедливости принципа максимума на решения необходимо накладывать дополнительные условия. Наиболее известные из них это условия Тихонова и Тэклинда. Нами показано, что для широкого класса нелинейных уравнений в подобных ограничениях нет необходимости. При этом мы допускаем произвольный рост коэффициентов при младщих членах при стремлении пространственной переменной к бесконечности.Приведен пример, демострирующий применение полученных результатов в случае нелинейности типа Эмдена-Фаулера.

Похожие темы научных работ по математике , автор научной работы — Коньков А.А.

On the maximum principle for a class of nonlinear parabolicequations

In this paper, we consider solutions of nonlinear parabolic equations in the half-space.It is well-known that, in the case of linear equations, one needs to impose additional conditions on solutions for the validity of the maximum principle. The most famous of them are the conditions of Tikhonov and T¨acklind. We show that such restrictions are not needed for a wide class of nonlinear equations. In so doing, the coefficients of lower-order derivatives can grow arbitrarily as the spatial variables tend to infinity.We give an example which demonstrates an application of the obtained results for nonlinearities of the Emden Fowler type.

Текст научной работы на тему «О принципе максимума для одного класса нелинейныхпараболических уравнений»

Вестник СамГУ. 2015. № 6(128)

О ПРИНЦИПЕ МАКСИМУМА ДЛЯ ОДНОГО КЛАССА НЕЛИНЕЙНЫХ ПАРАБОЛИЧЕСКИХ УРАВНЕНИЙ2

В статье исследуются решения нелинейных параболических уравнений в полупространстве.

Известно, что в случае линейных уравнений для справедливости принципа максимума на решения необходимо накладывать дополнительные условия. Наиболее известные из них — это условия Тихонова и Тэклинда. Нами показано, что для широкого класса нелинейных уравнений в подобных ограничениях нет необходимости. При этом мы допускаем произвольный рост коэффициентов при младщих членах при стремлении пространственной переменной к бесконечности.

Приведен пример, демострирующий применение полученных результатов в случае нелинейности типа Эмдена-Фаулера.

Ключевые слова: параболические уравнения, принцип максимума, нелинейные дифференциальные операторы, условие Тихонова, условие Тэклинда.

1. Предварительные сведения

E aj (x,t,u) qx qx bi(x,t,u) — — ut = f (x,t,u) в R++1, (1.1)

где R++1 = Rn x (0, го), n ^ 1, а \\aij(x,t,s)\\ — симметрическая матрица такая, что

для всех x = (xb . xn) G Rn, t £ (0, го), s G R \ <0>и £ = (£ь . £n) £ Rn \ <0>.

Будем предполагать, что найдутся локально ограниченные измеримые функции h : [0, го) ^ [0, го), п : [0, го) ^ [0, го) и p : [0, го) ^ [0, го) такие, что

inf h > 0, inf п > 0

!© Коньков А.А., 2015

Коньков Андрей Александрович (konkov@mech.math.msu.su), кафедра дифференциальных уравнений, Московский государственный университет имени М.В. Ломоносова, 119991, Российская Федерация, г. Москва, Ленинские горы, 1.

2Работа выполнена при поддержке гранта РФФИ 11-01-12018-офи-м-2011. Статья подготовлена по докладу конференции «СамДиф-2015».

для любого компакта K С (0, ж) и при этом

f (x,t,s)sign s > p(\x\)h(s) \aij(x,t,s)

f (x, t, s) sign s > p(\x\)n(s)^2 bi(x, t, s)xi

для всех (x,t) G R++1 и s G R \ <0>.

Определение 1.1. Решением уравнения (1.1) называется функция u, непрерывная в R++1, обладающая на этом множестве двумя непрерывными производными по переменным x = (xi. ,xn) и одной — по t и удовлетворяющая (1.1) в классическом смысле [6].

Вопросы, рассмотренные в этой статье, исследовались рядом авторов 6. Нашей целью является доказательство принципа максимума

sup \u\ ^ limsup \u(x,t)\ (1.2)

для решений уравнения (1.1). Хорошо извсетно, что в случае линейных уравнений для справедливости (1.2) на рост решений необходимо накладывать дополнительные условия [7; 8]. Ниже будет показано, что для широкого класса нелинейных уравнений эти условия могут быть сняты.

Для любой функции ф : [0, ж) ^ R и вещественного числа а > 1 обозначим

фа (r) = mf ф. 2. Основные результаты

Теорема 2.1. Пусть

(he(s)s)-1/2 ds 1 и а > 1. Тогда для любого решения (1.1) справедлив принцип максимума (1.2). Пример 2.1. Рассмотрим уравнение

Au + b(x)Du — ut = q(x)\u\x-iu в R++i, (2.1)

где D = (дХ1, дХ2. dXn) — оператор градиента, а b : Rn ^ Rn и q : Rn ^ [0, ж) — некоторые функции, удовлетворяющие условиям

для всех x G Rn и

т. е. существуют постоянные ci > 0 и С2 > 0 такие, что

для любого решения (2.1) справедлив принцип максимума (1.2).

Пусть теперь к > -1. В этом случае, взяв h(s) = n(s) = sx и

rl-k-1 при r ^ 1 и l > к — 1

для любого решения (2.1) справедлив принцип максимума (1.2).

[1] Ильин А.М., Калашников А.С., Олейник О.А. Линейные уравнения второго порядка параболического типа // УМН. 1962. Т. 17. № 3. С. 3-146.

[2] Кондратьев В.А. Об асимптотическом поведении решений нелинейных параболических уравнений второго порядка // Тр. МИАН. 2008. Т. 260. С. 180-192.

[3] Кондратьев В.А., Ландис Е.М. Качественная теория линейных дифференциальных уравнений в частных производных второго порядка // Итоги науки и техники. Сер.: Современные проблемы математики. Фундаментальные направления. 1988. Т. 32. С. 99-215.

[4] Коньков А.А. О стабилизации решений нелинейного уравнения Фоккера — Планка // Труды семинара имени И.Г. Петровского. 2013. Вып. 29. С. 333-345.

[5] Kon’kov A.A. On the asymptotic behaviour of solutions of nonlinear parabolic equations // Proc. Royal Soc. Edinburgh. 2006. V. 136. P. 365-384.

[6] Ландис Е.М. Уравнения второго порядка эллиптического и параболического типов. М.: Наука, 1971.

[7] ТаскИМ S. Sur les classes quasianalytiques des solutions des equations aux derivees partielles du type parabolique. // Nova Acta Soc. Sci. Uppsal. 1936. V. 4. Ser. 10. № 3. P. 1-57.

[8] Tychonoff A. Theoremes d’unicite pour l’equation de la chaleur // Матем. сб. 1935. Т. 42. № 2. С. 199-216.

[1] Il’in A.M., Kalashnikov A.S., Oleinik O.A. Linear equations of the second order of parabolic type. UMN [Russian Mathematical Surveys], 1962, Vol. 17, no. 3, pp. 1-146 [in Russian].

[2] Kondratiev V.A. On asymptotic behavior of solutions of nonlinear second-order parabolic equations. Tr. MIAN [Proceedings of Steklov Mathematical Institute, RAS], 2008, Vol. 260, pp. 172-184 [in Russian].

[3] Kondratiev V.A., Landis E.M. Qualitative theory of second order linear partial differential equations. M., VINITI, Itogi Nauki i Tekhniki. Ser. Sovrem. Probl. Mat. Fund. Napr., 1988, Vol. 32, pp. 99-215 [in Russian].

[4] Kon’kov A.A. Stabilization of solutions of the nonlinear Fokker-Planck equation. Trudy seminara imeni I.G. Petrovskogo [Proceedings of the seminar named after I.G. Petrovsky], 2014, Vol. 197, no. 3, pp. 358-366 [in Russian].

[5] Kon’kov A.A. On the asymptotic behaviour of solutions of nonlinear parabolic equations Proc. Royal Soc. Edinburgh, 2006, Vol. 136, pp. 365-384 [in English].

[6] Landis E.M. Second-order equations of elliptic and parabolic type. M., Nauka, 1971 [in Russian].

[7] Tâcklind S. Sur les classes quasianalytiques des solutions des equations aux derivees partielles du type parabolique. Nova Acta Soc. Sci. Uppsal., 1936, Vol. 4, Ser. 10, no. 3, pp. 1-57 [in Russian].

[8] Tychonoff A. Theoremes d’unicite pour l’equation de la chaleur. Matem. sb. [Mathematical collected book], 1935, Vol. 42, no. 2, pp. 199-216 [in French].

ON THE MAXIMUM PRINCIPLE FOR A CLASS OF NONLINEAR PARABOLIC EQUATIONS4

In this paper, we consider solutions of nonlinear parabolic equations in the half-space.

It is well-known that, in the case of linear equations, one needs to impose additional conditions on solutions for the validity of the maximum principle. The most famous of them are the conditions of Tikhonov and Tâcklind. We show that such restrictions are not needed for a wide class of nonlinear equations. In so doing, the coefficients of lower-order derivatives can grow arbitrarily as the spatial variables tend to infinity.

We give an example which demonstrates an application of the obtained results for nonlinearities of the Emden — Fowler type.

Key words: parabolic equations, maximum principle, nonlinear differential operators, Tikhonov’s condition, Tâacklind’s condition.

Статья поступила в редакцию 28/ V/2015. The article received 28/V/2015.

3 Kon’kov Andrej Alexandrovich (konkov@mech.math.msu.su), Department of Differential Equations, Lomonosov Moscow State University, 1, Leninskie Gory, Moscow, 119991, Russian Federation.

4The work is carried out with the support of grant of the Russian Foundation for Basic Research 11-01-12018-ofi-m-2011.