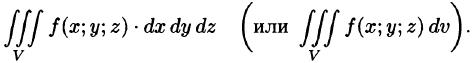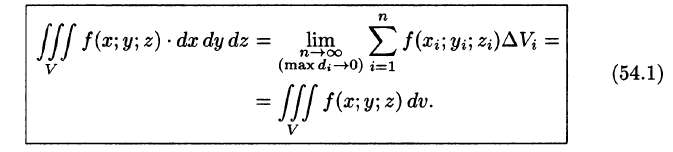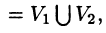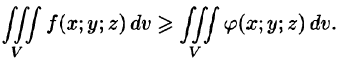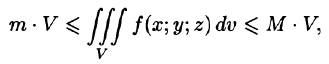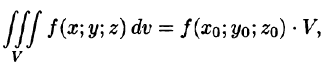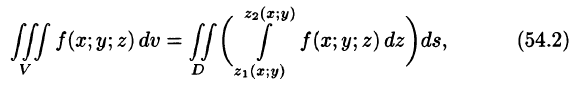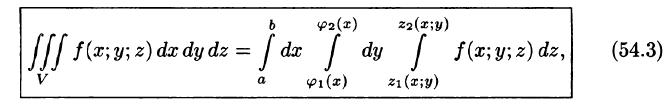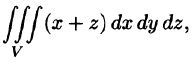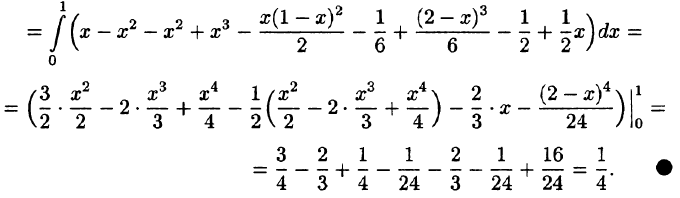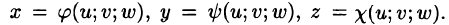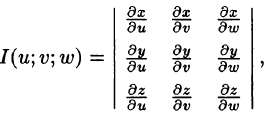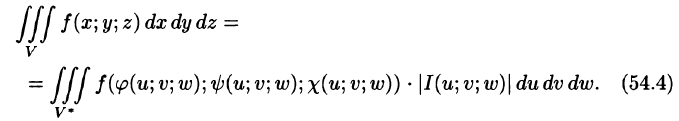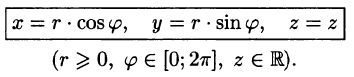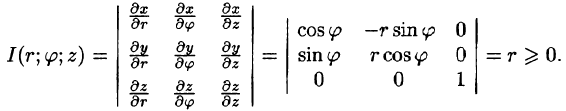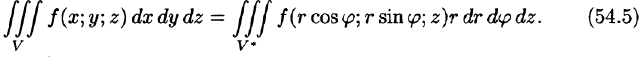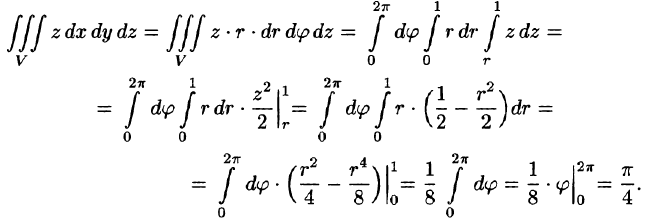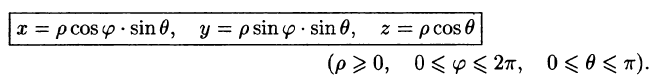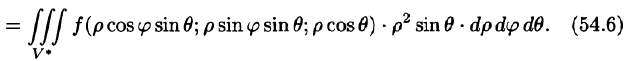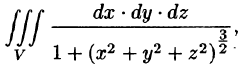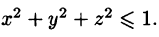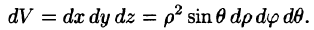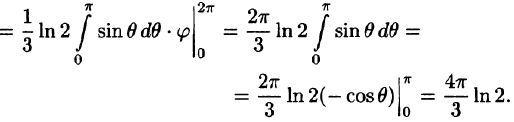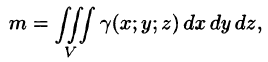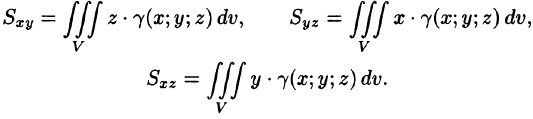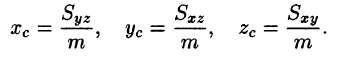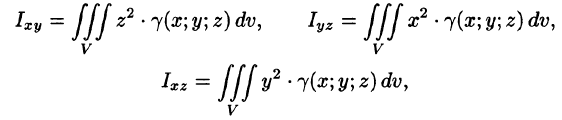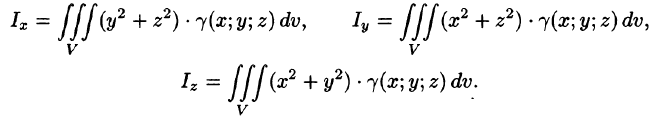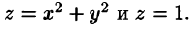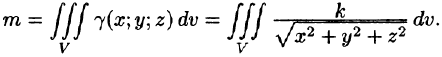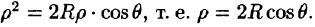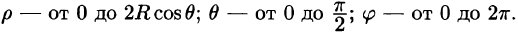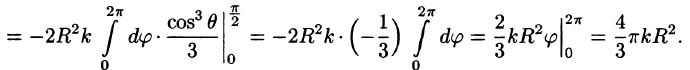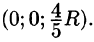Лекция № 8
Ссылки
10.2. Уравнения прямой на плоскости
Простейшей из линий является прямая. Разным способам задания прямой соответствуют в прямоугольной системе координат разные виды её уравнений.
Уравнение прямой с угловым коэффициентом
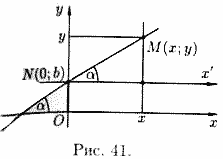
Пусть на плоскости Оху задана произвольная прямая, не параллельная оси Оу. Ее положение вполне определяется ординатой b точки N(0; b) пересечения с осью Оу и углом a между осью Ох и прямой (см. рис. 41).
Из определения тангенса угла следует равенство
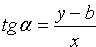
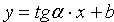
Введем обозначение tg a=k , получаем уравнение
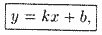
которому удовлетворяют координаты любой точки М(х;у) прямой. Можно убедиться, что координаты любой точки Р(х;у), лежащей вне данной прямой, уравнению (10.2) не удовлетворяют.
Число k = tga называется угловым коэффициентом прямой, а уравнение (10.2) — уравнением прямой с угловым коэффициентом.
Если прямая проходит через начало координат, то b = 0 и, следовательно, уравнение этой прямой будет иметь вид y=kx .
Если прямая параллельна оси Ох, то a = 0, следовательно, k = tga = 0 и уравнение (10.2) примет вид у = b.
Если прямая параллельна оси Оу, то 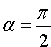
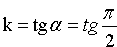
В этом случае уравнение прямой будет иметь вид
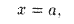
где a — абсцисса точки пересечения прямой с осью Ох. Отметим, что уравнения (10.2) и (10.3) есть уравнения первой степени.
Общее уравнение прямой.
Рассмотрим уравнение первой степени относительно x и y в общем виде
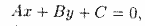
где А, В, С — произвольные числа, причем А и В не равны нулю одновременно.
Покажем, что уравнение (10.4) есть уравнение прямой линии. Возможны два случая.
Если В = 0, то уравнение (10.4) имеет вид Ах + С = О, причем А ¹ 0 т. е. 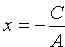
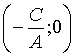
Если B ¹ 0, то из уравнения (10.4) получаем 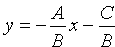
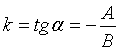
Итак, уравнение (10.4) есть уравнение прямой линии, оно называется общим уравнением прямой.
Некоторые частные случаи общего уравнения прямой:
1) если А = 0, то уравнение приводится к виду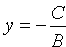
2) если В = 0, то прямая параллельна оси Оу;
3) если С = 0, то получаем 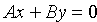
Уравнение прямой, проходящей через данную точку в данном направлении
Пусть прямая проходит через точку 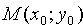
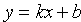
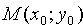
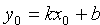
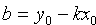
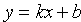
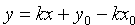
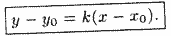
Уравнение (10.5) с различными значениями k называют также уравнениями пучка прямых с центром в точке 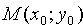
Уравнение прямой, проходящей через две точки
Пусть прямая проходит через точки 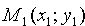
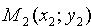

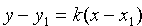
где k — пока неизвестный коэффициент.
Так как прямая проходит через точку 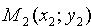
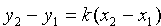
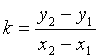
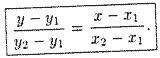
Предполагается, что в этом уравнении 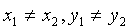
Если x2 = x1 прямая, проходящая через точки 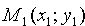
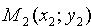
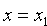
Если y2 = y1 то уравнение прямой может быть записано в виде 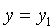
Уравнение прямой в отрезках
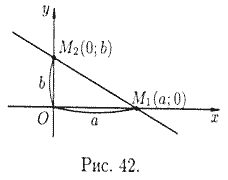
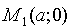
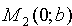
Это уравнение называется уравнением прямой в отрезках, так как числа α и b указывают, какие отрезки отсекает прямая на осях координат.
Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
Найдем уравнение прямой, проходящей через заданную точку 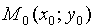
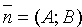
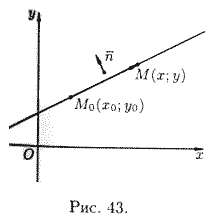
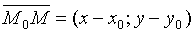
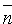
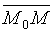
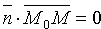
Уравнение (10.8) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору.
Вектор 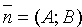
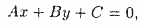
где А и B— координаты нормального вектора, 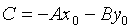
Полярное уравнение прямой
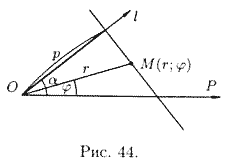
Для любой точки 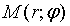
С другой стороны,
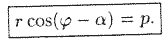
Полученное уравнение (10.10) и есть уравнение прямой в полярных координатах.
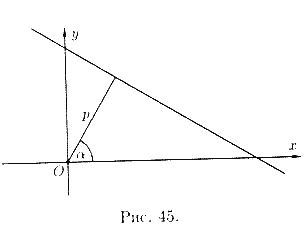
Нормальное уравнение прямой
Пусть прямая определяется заданием p и α (см. рис. 45). Рассмотрим прямоугольную систему координат 


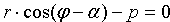
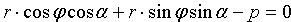
Но, в силу формул, связывающих прямоугольные и полярные координаты, имеем: 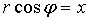
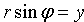
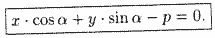
Уравнение (10.11) называется нормальным уравнением прямой.
Умножим все члены уравнения (10.4) на некоторый множитель 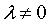
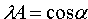
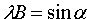
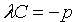
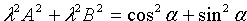
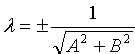
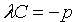
10.3 Прямая линия на плоскости. Основные задачи
Угол между двумя прямыми и условия параллельности и перпендикулярности двух прямых
Пусть прямые L1 и L2 заданы уравнениями с угловыми коэффициентами 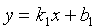
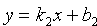
Требуется найти угол φ, на который надо повернуть в положительное направлении прямую L1 вокруг точки их пересечения до совпадения с прямой L2.
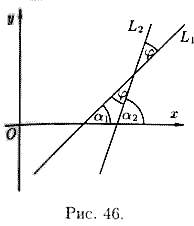
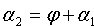
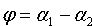
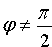
Но 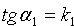
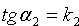

откуда легко получим величину искомого угла.
Если требуется вычислить острый угол между прямыми, не учитывая, какая прямая является первой, какая — второй, то правая часть формулы (10.12) берется по модулю, т. е.
Если прямые L1 и L2 параллельны, то φ = 0 и 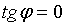
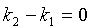
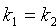
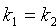
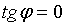
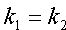
Если прямые L1 и L2 перпендикулярны, то 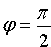
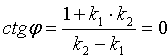
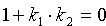
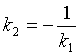
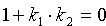
Расстояние от точки до прямой
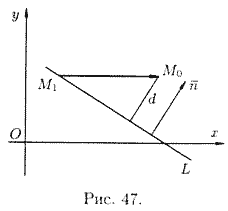
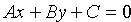
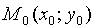
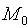
Решение : Расстояние d отточки 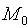
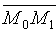
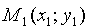
вектора 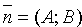
Так как точка 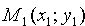
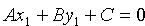
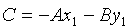
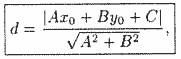
что и требовалось получить.
§11. ЛИНИИ ВТОРОГО ПОРЯДКА НА ПЛОСКОСТИ
11.1. Основные понятия
Рассмотрим линии, определяемые уравнениями второй степени относительно текущих координат
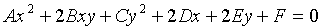
Коэффициенты уравнения — действительные числа, но по крайней мере одно из чисел А, В или С отлично от нуля. Такие линии называются линиями (кривыми) второго порядка. Ниже будет установлено, что уравнение (11.1) определяет на плоскости окружность, эллипс, гиперболу или параболу. Прежде, чем переходить к этому утверждению, изучим свойства перечисленных кривых.
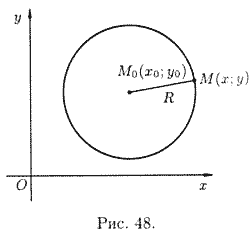
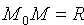
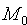
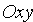
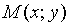
Тогда из условия 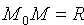
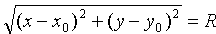
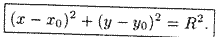
Уравнению (11.2) удовлетворяют координаты любой точки 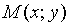
Уравнение (11.2) называется каноническим уравнением окружности
В частности, полагая 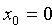
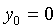
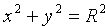
Уравнение окружности (11.2) после несложных преобразований примет вид 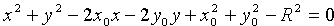
1) коэффициенты при x 2 и у 2 равны между собой;
2) отсутствует член, содержащий произведение xу текущих координат.
Рассмотрим обратную задачу. Положив в уравнении (11.1) значения 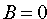
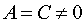
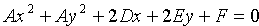
Преобразуем это уравнение:
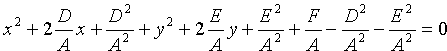
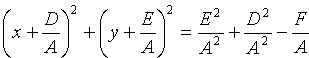
Отсюда следует, что уравнение (11.3) определяет окружность при условии 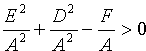
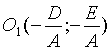
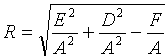
Если же 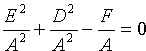
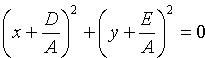
Ему удовлетворяют координаты единственой точки 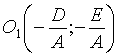
Если 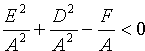
Каноническое уравнение эллипса
Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
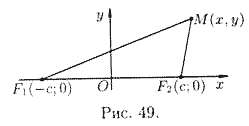
Для вывода уравнения эллипса выберем систему координат 

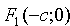
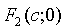
Пусть 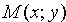
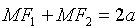
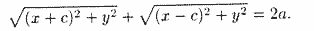
Это, по сути, и есть уравнение эллипса.
Преобразуем уравнение (11.5) к более простому виду следующим образом:
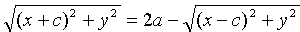
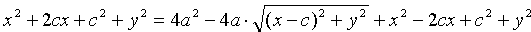
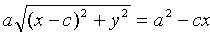
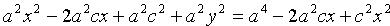
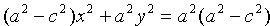
Так как a>с, то 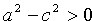

Тогда последнее уравнение примет вид 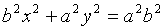
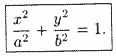
Можно доказать, что уравнение (11.7) равносильно исходному уравнению. Оно называется каноническимуравнением эллипса.
Эллипс — кривая второго порядка.
Исследование формы эллипса по его уравнению
Установим форму эллипса, пользуясь его каноническим уравнением.
1. Уравнение (11.7) содержит х и у только в четных степенях, поэтому если точка 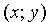
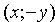
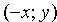
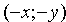

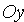
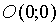
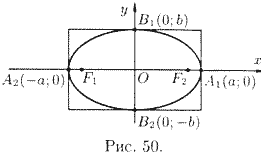
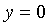
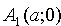
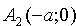

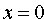
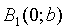
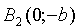
3. Из уравнения (11.7) следует, что каждое слагаемое в левой части не превосходит единицы, т.е. имеют место неравенства 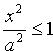
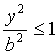
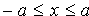
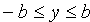
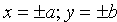
4. В уравнении (11.7) сумма неотрицательных слагаемых 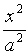
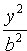
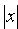
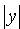
Из сказанного следует, что эллипс имеет форму, изображенную на рис. 50 (овальная замкнутая кривая).
Дополнительные сведения об эллипсе
Форма эллипса зависит от отношения 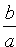
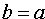
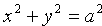
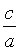
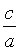
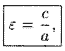
Базовый уровень
Велосипедист, двигаясь равномерно, проезжает 20м за 2с.
Определите, какой путь он проедет при движении с той же скоростью за 10с.
v=20:2=10м/c
s=10.10=100м
2. На рисунке 23 приведен график зависимости пути при движении
велосипедиста от времени. Определите по этому графику путь,
который проехал велосипедист в промежуток времени от 1 до 4с.

рис.23 рис.24 рис.25
3. По графику (см. рис.23) определите скорость движения велосипедиста
в момент времени t = 2c.
Ответ: v=3м/c
4. На рис.24 представлены графики движения трех тел.
Какое из этих тел движется с наибольшей по модулю скоростью
в момент времени t = 5c.
Ответ: v3=-4м/c
5. По графику (см. рис.24) определите скорость движения первого тела
в момент времени t = 5c.
Ответ: v=0
6. По графику (см. рис.25) определите время и место встречи первого и второго тел.
Ответ: t=5с x = 15м
7. Запишите уравнение движения x = x(t) второго тела (см. рис.25).
Ответ: x = 3 t.
8. Движение тела описывается уравнением x = 4 – t.
На каком из графиков (рис.26) представлена зависимость
координаты этого тела от времени?
Уравнение движения лыжника имеет вид х = –20+5t. Постройте график x(t).
Определите: а) координату лыжника через 10 с;
б) где был лыжник за 5 с до начала наблюдения;
в) когда он будет на расстоянии 80 м от начала координат.
а) t = 10c x = 30м
б) t = 5c x = -45м
в) х = 80м t = 20c
При движении вдоль оси ОХ координата точки изменилась за 8 с от значения x1=9 м до значения x2=17 м. Запишите формулу зависимости x(t). Скорость считать постоянной.
Вдоль оси ОХ движутся два тела, координаты которых изменяются согласно формулам: x1=10+2t и х2=4+5t. В какой момент времени тела встретятся?
Найдите координату точки встречи.
Вдоль оси ОХ движутся два тела, координаты которых изменяются согласно формулам: х1=20 — 4t и х2=10 + t. В какой момент времени тела встретятся?
Найдите координату точки встречи. Задачу решить графически.

зависимости vx(t).
Поезд длиной 240 м, двигаясь равномерно, прошел мост за 2 мин.
Какова скорость поезда, если длина моста 360 м?
 | ||||||
Последний вагон поезда проехал s=240+360=600м за t=120c, Автомобиль, двигаясь со скоростью 30 км/ч, проехал половину пути до места назначения за 2 ч. С какой скоростью он должен продолжить движение, чтобы достигнуть цели и вернуться обратно за то же время?
Движение материальной точки в плоскости ХОУ описывается уравнениями: х=6+3t, у=4t. На рисунке изображен график зависимости координаты материальной точки от времени. Построить график проекции скорости в зависимости от времени.
19. Наблюдая с платформы за равномерно движущимся поездом, мальчик определил,
Последний вагон поезда проехал мимо платформы длиной 120 м за 16 с, значит его скорость v=120/16=7,5м/с |

С какой скоростью он двигался, если увеличив скорость до 25 км/ч,
он за следующий час добрался до поселка Б и вернулся в поселок А?
v.1= 3s
v= 3s
Тройной интеграл с примерами решения и образцами выполнения
Обобщением определенного интеграла на случай функции трех переменных является так называемый «тройной интеграл».
Теория тройного интеграла аналогична теории двойного интеграла. Поэтому изложим ее в несколько сокращенном виде.
Пусть в замкнутой области V пространства Oxyz задана непрерывная функция и = f(x;y;z). Разбив область V сеткой поверхностей на п частей 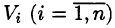
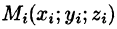
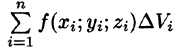
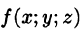
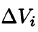
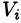
Если предел интегральной суммы существует при неограниченном увеличении числа п таким образом, что каждая «элементарная область» 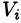
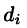
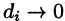
Таким образом, по определению, имеем:
Здесь dv = dx dy dz — элемент объема.
Теорема:
Если функция и = f(x;y,z) непрерывна в ограниченной замкнутой области V, то предел интегральной суммы (54.1) при 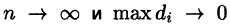
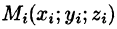
Тройной интеграл обладает теми же свойствами, что и двойной интеграл:
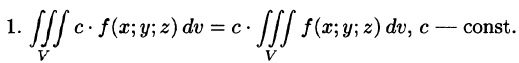
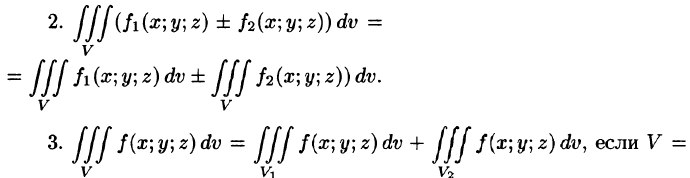
а пересечение 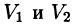
4. 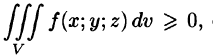
Если в области интегрирования 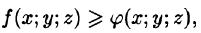
5.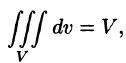
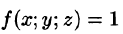
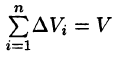
6. Оценка тройного интеграла:
где m и М — соответственно наименьшее и наибольшее значения функции f(x;y;z) в области V.
7. Теорема о среднем значении: если функция f(x; у, z) непрерывна в замкнутой области V, то в этой области существует такая точка 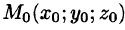
где V — объем тела.
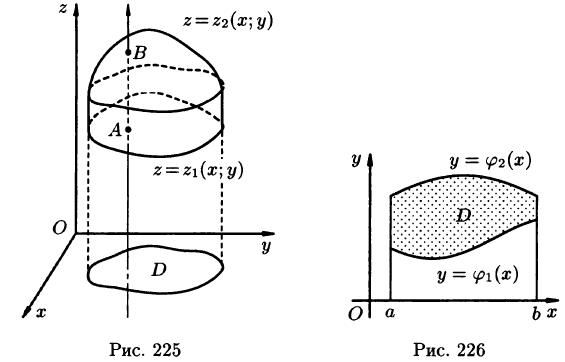
Вычисление тройного интеграла в декартовых координатах
В декартовых координатах вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов.
Пусть областью интегрирования V является тело, ограниченное снизу поверхностью 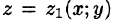
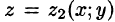
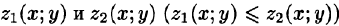
сводящая вычисление тройного интеграла к вычислению двойного интеграла от однократного (доказательство формулы (54.2) не приводим). При этом сначала вычисляется внутренний интеграл по переменной г при постоянных х и у в пределах изменения z. Нижней границей интеграла является аппликата точки А — точки входа прямой, параллельной оси Oz в область V, т. е. 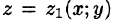
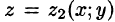
Если область D ограничена линиями 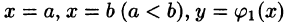
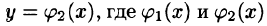
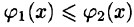
по которой вычисляется тройной интеграл в декартовых координатах.
Замечания:
- Если область V более сложная, чем рассмотренная, то ее следует разбить на конечное число таких областей (правильных), к которым можно применить формулу (54.3).
- Порядок интегрирования в формуле (54.3), при определенных условиях, может быть иным.
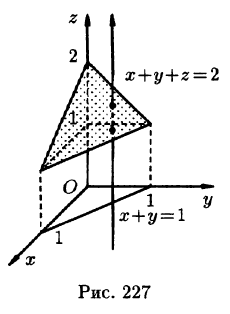
Пример:
где V ограничена плоскостями х = 0, у =0, z = 1, x + y + z = 2 (рис. 227).
Решение:
Область V является правильной в направлении оси Oz (как, заметим, и в направлении осей Ох и Оу). Ее проекция на плоскость Оху является правильной в направлении оси Оу (и оси Ох). Согласно формуле (54.3), имеем:
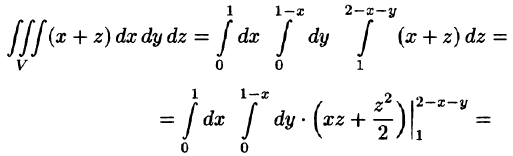
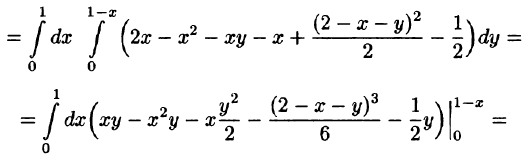
Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах
При вычислении тройного интеграла, как и двойного, часто применяется метод подстановки, т. е. совершается преобразование переменных.
Пусть совершена подстановка
Если эти функции имеют в некоторой области 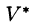
то справедлива формула замены переменных в тройном интеграле:
Здесь I(u; v;w) — определитель Якоби, или якобиан преобразования (примем без доказательства).
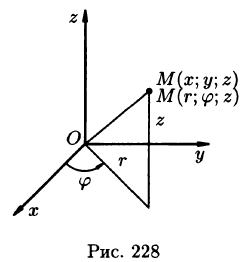
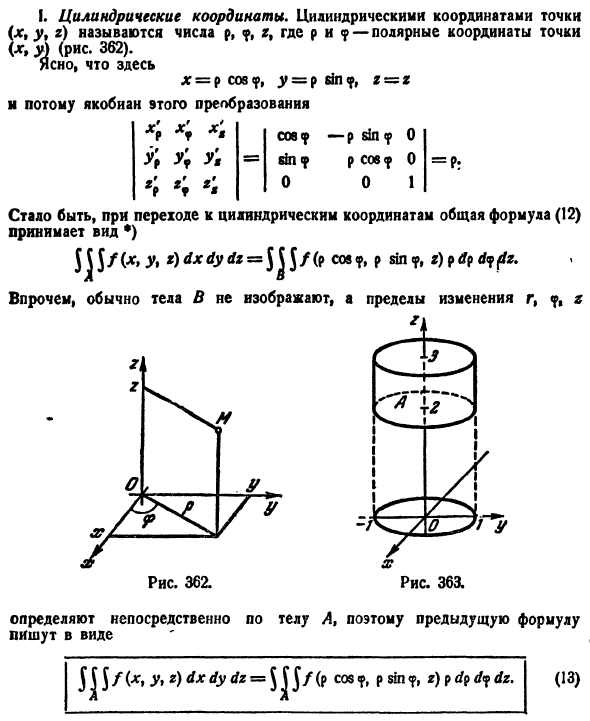
Для вычисления тройного интеграла часто используют так называемые цилиндрические координаты.
Положение точки М(х; у; z) в пространстве Oxyz можно определить заданием трех чисел 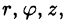
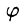
Эти три числа (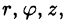
Цилиндрические координаты точки связаны с ее декартовыми координатами следующими соотношениями:
Возьмем в качестве и, v, w цилиндрические координаты 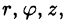
Формула замены переменных (54.4) принимает вид
Таким образом, вычисление тройного интеграла приводится к интегрированию по r, по 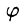
Замечание:
К цилиндрическим координатам бывает удобно перейти в случае, если область интегрирования образована цилиндрической поверхностью.
Пример:
Вычислить 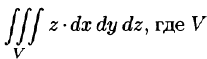
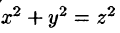
Решение:
На рис. 229 изображена область интегрирования V. Вычислим интеграл путем перехода к цилиндрическим координатам: 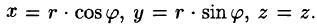
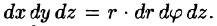
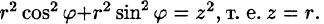
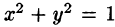
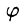
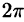
Таким образом, согласно формуле (54.5), получаем:
Заметим, что, не переходя к цилиндрическим координатам, получим:
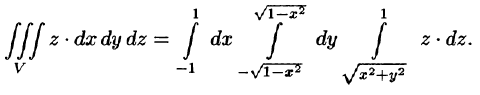
Сферическими координатами точки М(х; у; z) пространства Oxyz называется тройка чисел 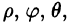
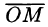
Сферические координаты 
В некоторых случаях вычисление тройного интеграла удобно производить, перейдя к сферическим координатам. Для этого нужно воспользоваться формулой замены переменных в тройном интеграле (54.4). Так как якобиан преобразования
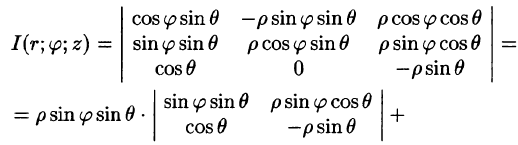
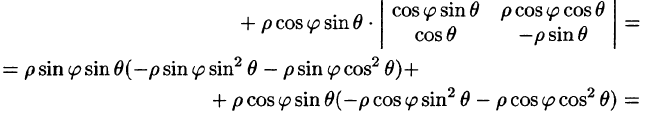
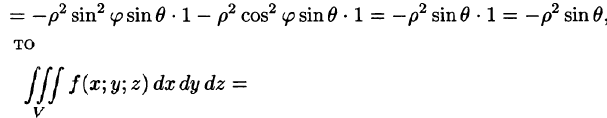
Замечание:
Переходить к сферическим координатам удобно, когда область интегрирования V есть шар (уравнение его границы 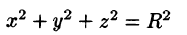
Пример 54.3. Вычислить
где V — шар
Решение:
Вычислим интеграл путем перехода к сферическим координатам: 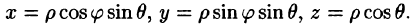
Граница области V — сфера и ее уравнение имеет вид р = 1, подынтегральная функция после замены переменных примет вид 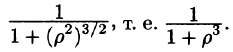
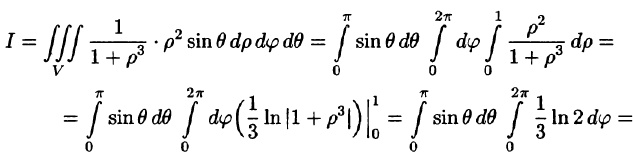
Некоторые приложения тройного интеграла Объем тела
Объем области V выражается формулой 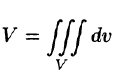
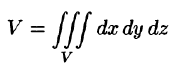
Масса тела
Масса тела m при заданной объемной плотности 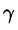
где 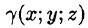
Статические моменты
Моменты 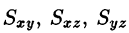
Центр тяжести тела
Координаты центра тяжести тела V находятся по формулам
Моменты инерции тела
Моменты инерции тела относительно координатных плоскостей вычисляются по формулам
а моменты инерции относительно координатных осей:
Пример:
Найти объем тела, ограниченного поверхностями
Решение:
Данное тело ограничено сверху плоскостью z = 1, снизу — параболоидом 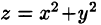
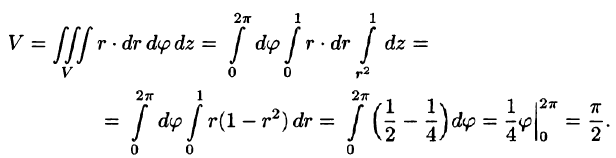
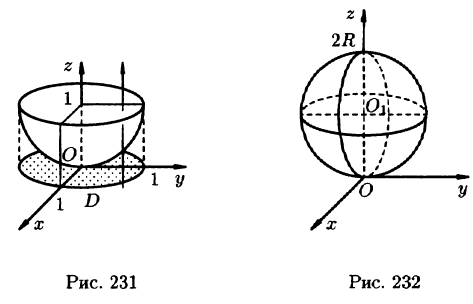
Пример:
Найти массу шара 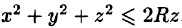
Решение:
Уравнение сферы 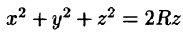
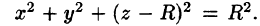
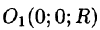
где k — коэффициент пропорциональности, 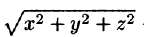
Итак,
Вычислять интеграл будем в сферических координатах. Уравнение сферы 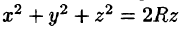
Поэтому сферические координаты будут изменяться в следующих пределах:
Подынтегральная функция примет вид 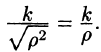
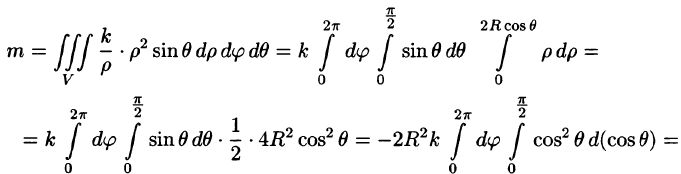
Из соображений симметрии следует, что 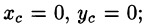
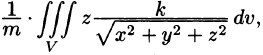
Тройной интеграл


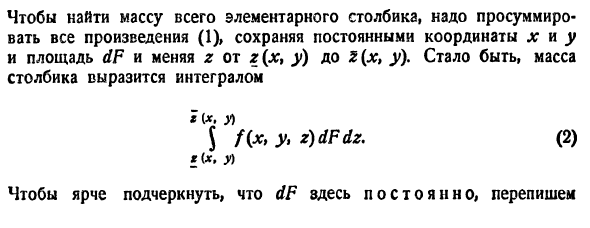

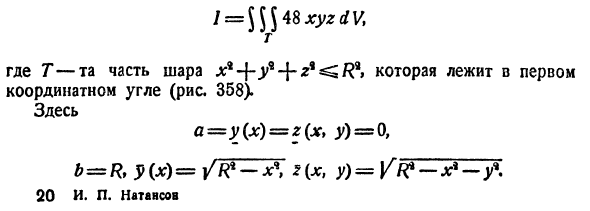

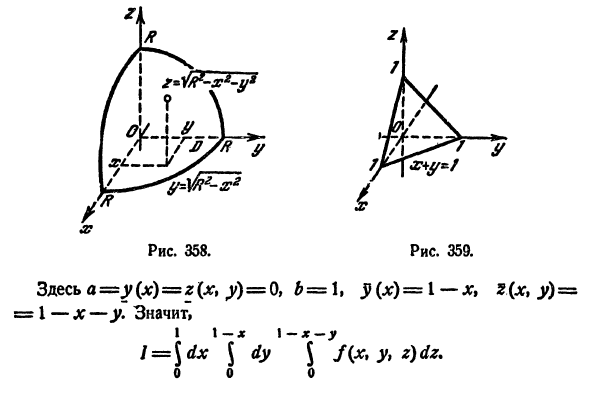

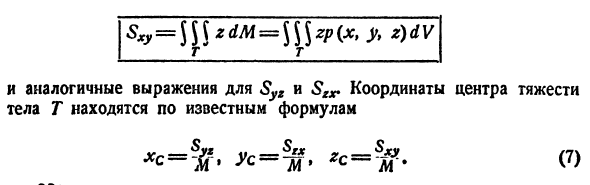









Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://pandia.ru/text/78/161/11842.php
http://lfirmal.com/trojnoj-integral/
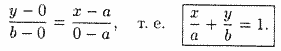
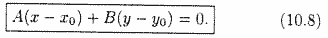
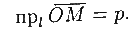
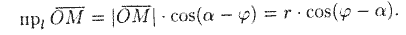
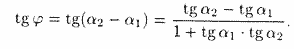
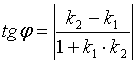
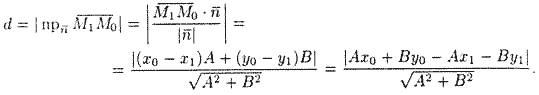
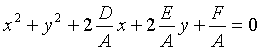












 На рисунке изображен график зависимости координаты материальной точки от времени.
На рисунке изображен график зависимости координаты материальной точки от времени.