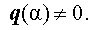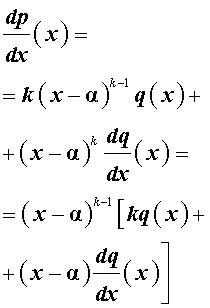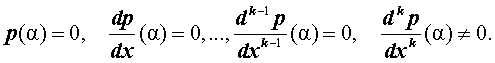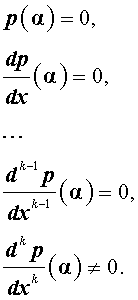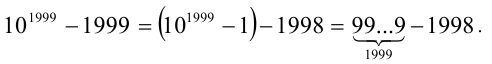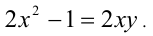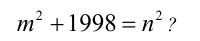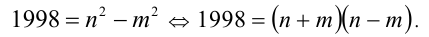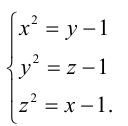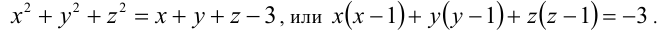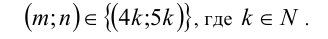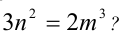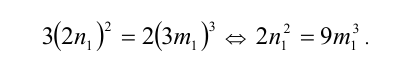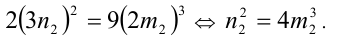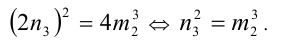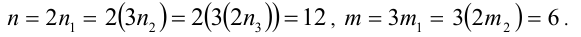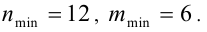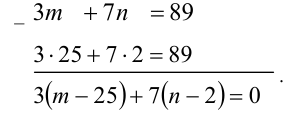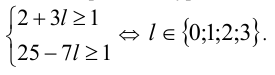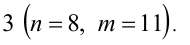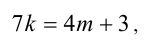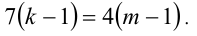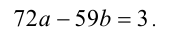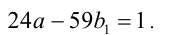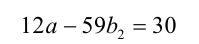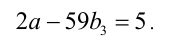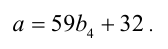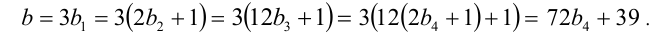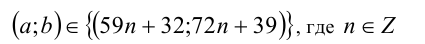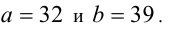Кратные корни многочленов
Пусть p(x) – многочлен степени n , а q(x) – многочлен степени n – k , где n и k – натуральные числа, удовлетворяющие неравенству 
Определение . Число α называют корнем кратности k многочлена p(x) , если справедливо равенство
| p(x) = (x – α) k q (x) , | (1) |
Утверждение 1 . Число α является корнем кратности k многочлена p(x) тогда и тогда, когда оно является корнем производной этого многочлена кратности k – 1 .
Доказательство . Взяв производную от обеих частей формулы (1), получаем
Поскольку выражение, стоящее в квадратных скобках, при x = α не обращается в нуль, то утверждение 1 доказано.
Из утверждения 1 вытекает следующее
Утверждение 2 . Число α является корнем кратности k многочлена p(x) тогда и тогда, когда выполнены равенства:
Задача . Найти все значения параметра m , при которых многочлен
имеет корень кратности 2 .
Решение . Воспользовавшись утверждением 2, получаем
Метод анализа делимости нацело
Метод анализа делимости нацело. Использование признаков делимости
Рассмотрим примеры, когда при решении задачи возникает необходимость проанализировать делимость нацело того или иного целочисленного выражения.
Пример №7.
Доказать, что при любом натуральном п выражение 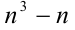
Решение:
Преобразуем выражение к виду 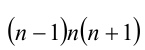
Замечание. Аналогичными рассуждениями можно доказать, что произведение четырёх последовательных натуральных чисел делится нацело на 24.
Пример №8.
Доказать, что число 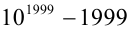
Решение:
Преобразуем число к виду
Каждое из двух слагаемых делится нацело на 9 по признаку делимости на 9. Следовательно, их разность также кратна 9, что и требовалось доказать.
Пример №9.
Найти все числа вида 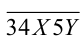
Решение:
Поскольку 36 = 4 • 9 , то воспользуемся признаками делимости на 4 и 9. Начнём с признака делимости на 4 (он использует только одну из двух неизвестных цифр). Число 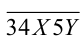
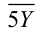
1) Если Y = 2, то число 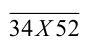
2) Если Y = 6, то число 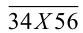
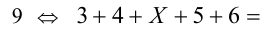
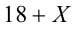
Пример №10.
Решить уравнение в целых числах
Решение:
Заметим, что при целых X и Y в левой части уравнения стоит нечётное число, а в правой — чётное, что невозможно. Следовательно, данное уравнение не имеет решений в целых числах.
Пример №11.
Доказать, что уравнение 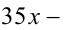
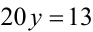
Доказательство. Достаточно заметить, что при целых X и Y выражение в левой части уравнения делится нацело на 5, а число 13 справа — нет. Полученное противоречие доказывает утверждение.
Пример №12.
Существуют ли целые числа т и п , удовлетворяющие уравнению
Решение:
Преобразуем уравнение к виду
Так как 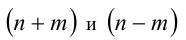
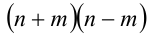
Ответ: не существуют.
Пример №13.
Решить в целых числах систему уравнений
Решение:
1-й способ. Из первого уравнения системы следует, что числа x и у имеют разную чётность (если одно четно, то другое — нечётно, и наоборот). Из второго уравнения аналогично следует, что у и z — разной чётности, а из третьего, что X и Z также имеют разную чётность, что невозможно.
2-й способ. Сложив все три уравнения системы, получим следствие
Левая часть последнего равенства чётна как сумма трёх чётных чисел (поскольку произведение любых двух последовательных целых чисел всегда чётно), а правая часть — нечётна, что невозможно. Ответ: нет решений в целых числах.
Пример №14.
Известно, что 4п = 5т . Найти все натуральные числа т и n , удовлетворяющие этому равенству.
Решение:
Целочисленное выражение 4n в левой части равенства кратно 4, следовательно, и выражение 5т справа также должно делиться на 4 нацело. Но так как 5 на 4 нацело не делится, то, значит,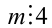
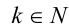
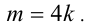
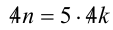
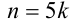
Пример №15.
При каких наименьших натуральных значениях n и m выполняется равенство
Решение:
1) Заметим, что левая часть уравнения 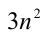
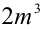
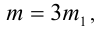
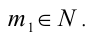
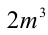
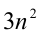
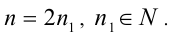
2) Так как 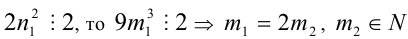
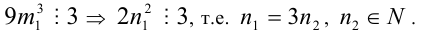
3) Так как 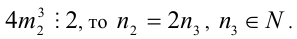
Очевидно, что последнее равенство выполняется при 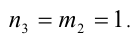
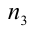
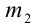
Ответ:
Подбором одного из решений с последующим анализом делимости решаются в простейших случаях линейные диофантовы уравнения.
Пример №16.
На какую минимальную величину могут отличаться друг от друга натуральные числа т и п, если известно, что дробь 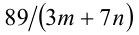
Решение:
Так как число 89 — простое (убедитесь в этом сами), то данная дробь является натуральным числом тогда и только тогда, когда выражение 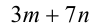
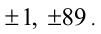
Это линейное диофантово уравнение. Решим его. Очевидно, пара чисел 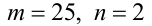
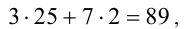
Переписав последнее уравнение в виде
воспользуемся анализом делимости левой и правой частей. Так, поскольку левая часть уравнения (2) делится нацело на 3, то и правая часть, т.е. выражение 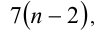
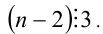
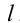
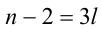
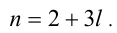
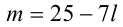
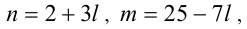
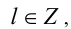
Тогда 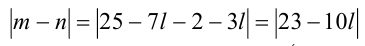
Пример №17.
Целое число кратно 7 и при делении на 4 даёт в остатке 3. Найти остаток от деления этого числа на 28.
Решение:
По условию 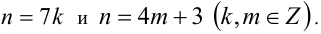
которое необходимо решить в целых числах. Подберём любую пару целых чисел (k,m), удовлетворяющих уравнению, например (l,l). Вычитая из уравнения тождество 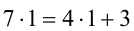
В последнем уравнении выражение справа делится нацело на 4, следовательно, 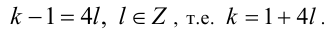
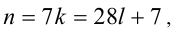
В более сложных случаях, когда подобрать решение затруднительно, последовательное применение рассмотренного подхода, основанного на анализе делимости нацело, тем не менее, помогает справиться с проблемой.
Пример №18.
Найти хотя бы одну пару целых чисел а и b , удовлетворяющих соотношению
Решение:
1) Так как 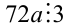
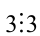
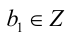
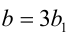
2) Продолжаем анализировать делимость. Поскольку в последнем равенстве число 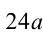
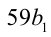
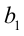
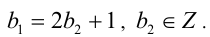
(коэффициент при а стал ещё меньше).
3) Так как 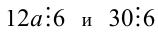
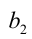
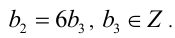
4) Из последнего уравнения анализом делимости на 2 получаем, что 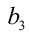
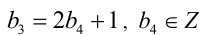
Осталось найти b :
Таким образом, множество всех целочисленных решений исходного уравнения имеет вид
(мы переобозначили для простоты 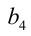
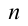
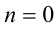
Заметим в заключение, что изначально подобрать какое-либо одно решение в данной задаче было весьма затруднительно.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Метод математической индукции для чайников
Метод полного перебора конечного числа случаев, исчерпывающих все возможности, называется полной индукцией. Этот метод имеет крайне ограниченную область применения в математике, так как обычно математические утверждения касаются бесконечного множества объектов (например, натуральных чисел, простых чисел, квадратов и т.п.) и перебрать их невозможно.
Существует метод рассуждений, который позволяет заменить неосуществимый бесконечный перебор доказательством того, что если утверждение истинно в одном случае, то оно окажется истинным и в следущем за ним случае. Этот метод носит название математической индукции (или рассуждением от $n$ к $n+1$)
Основы метода математической индукции
В основе метода математической индукции (ММИ) лежит принцип математической индукции: утверждение $P(n)$ (где $n$ — натуральное число) справедливо при $\forall n \in N$, если:
- Утверждение $P(n)$ справедливо при $n=1$.
- Для $\forall k \in N$ из справедливости $P(k)$ следует справедливость $P(k+1)$.
Доказательство с помощью метода математической индукции проводится в два этапа:
- База индукции (базис индукции). Проверяется истинность утверждения при $n=1$ (или любом другом подходящем значении $n$)
- Индуктивный переход (шаг индукции). Считая, что справедливо утверждение $P(k)$ при $n=k$, проверяется истинность утверждения $P(k+1)$ при $n=k+1$.
Метод математической индукции применяется в разных типах задач:
- Доказательство делимости и кратности
- Доказательство равенств и тождеств
- Задачи с последовательностями
- Доказательство неравенств
- Нахождение суммы и произведения
Ниже вы найдете примеры решения задач, иллюстрирующие применение метода математической индукции, а также ссылки на полезные сайты и учебник и небольшой видеоурок по ММИ.
Математическая индукция: задачи и решения
Доказательство кратности и делимости
Задача 1. Докажите, что $5^n-4n+15$ делится на 16 при всех $n \in N_0$.
Задача 2. Доказать, что при любом натуральном $n$ число $a_n$ делится на $b$.
$$a_n = 2n^3+3n^2+7n, \quad b=6.$$
Задача 3. Докажите методом математической индукции: $4^ <2n-1>+ 1$ кратно 5 для всех $n \ge 1$.
Задача 4. Используя метод математической индукции, докажите, что для любого натурального числа истинно следующее утверждение: $6^<2n-2>+3^
Доказательство равенств и неравенств
Задача 5. Доказать равенство
Задача 6. Доказать методом математической индукции:
Задача 7. Доказать неравенство:
Задача 8. Доказать утверждение методом математической индукции:
$$ \left(1-\frac<1><4>\right)\left(1-\frac<1><9>\right)\left(1-\frac<1><16>\right)\cdot . \cdot\left(1-\frac<1>
Задача 9. Доказать неравенство:
$$ 2!\cdot 4! \cdot . \cdot (2n)! \gt [(n+1)!]^n \quad (n \gt 2).$$
Задача 10. Докажите методом математической индукции неравенство Бернулли: $(1+a)^n \gt 1 + a\cdot n$ для всех $n\in N$ и $a \gt -1$, $a \in R$.
Вычисление сумм
Задача 11. Доказать методом математической индукции:
Задача 12. Найдите сумму
$$1 \cdot 1! + 2 \cdot 2! + . . . + 2012 \cdot 2012! + 2013 \cdot 2013!$$
Заказать решение
Если вам нужна помощь с решением задач по любым разделам математики, обращайтесь в МатБюро. Выполняем контрольные и практические работы, ИДЗ и типовые расчеты на заказ. Стоимость задания от 60 рублей , оформление производится в Word, срок от 2 дней.
Полезные ссылки о ММИ
- ММИ: краткая теория и примеры решений Страничка виртуальной школы юного математика. Разобраны примеры (в том числе для геометрии) и даны задачи для самостоятельной работы.
- Виленкин Н.Я. Индукция. Комбинаторика Классическое пособие по методу математической индукции и комбинаторике (базовые понятия и примеры задач).
- Математическая индукция. Основные определения и 10 разобранных решений.
- Николаева С.А. Метод математической индукции: методическое пособие для учителей и учащихся.
- А. Шень Математическая индукция. Пособие для школьников, разобраны 29 задач, из них 19 с полным решением.
Кратенький видеоурок о ММИ
http://lfirmal.com/metod-analiza-delimosti-natselo-v-matematike/
http://www.matburo.ru/ex_dm.php?p1=dmmmi