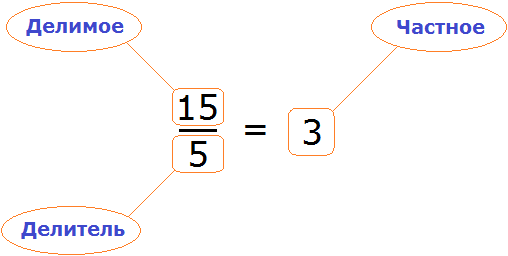
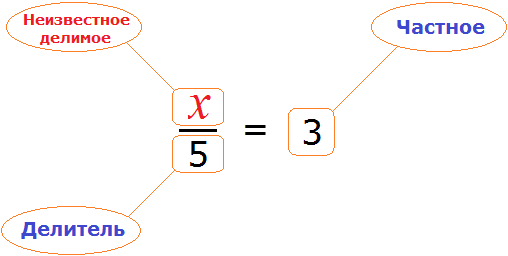
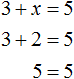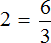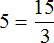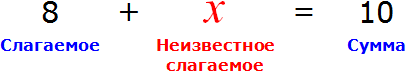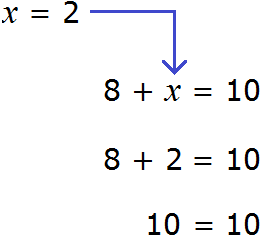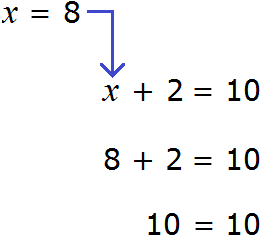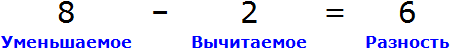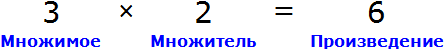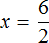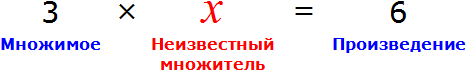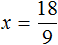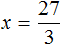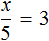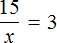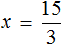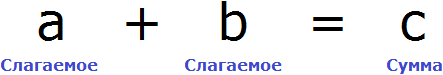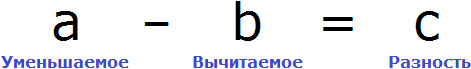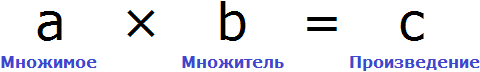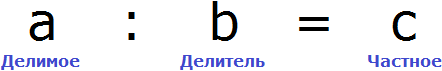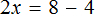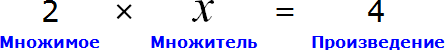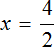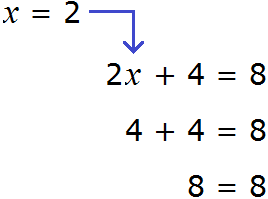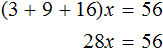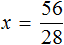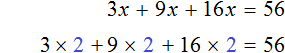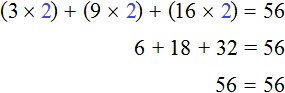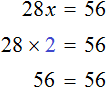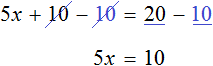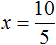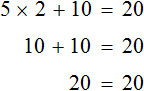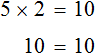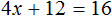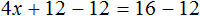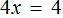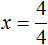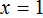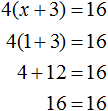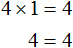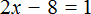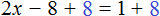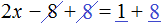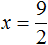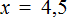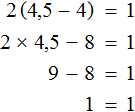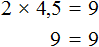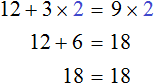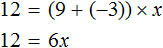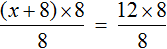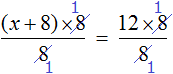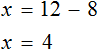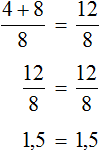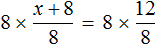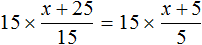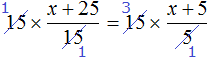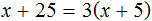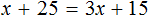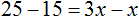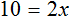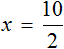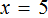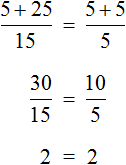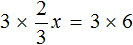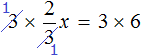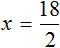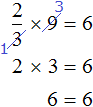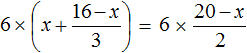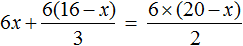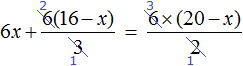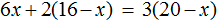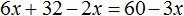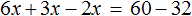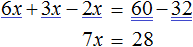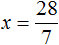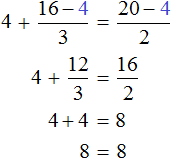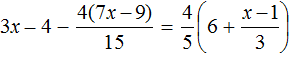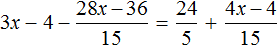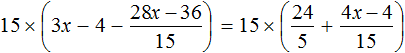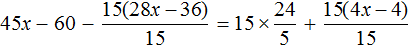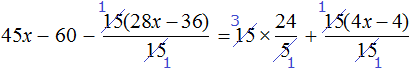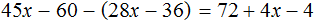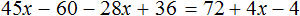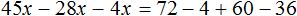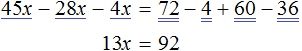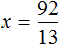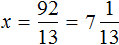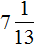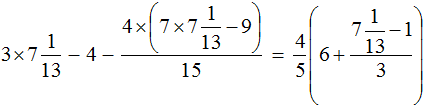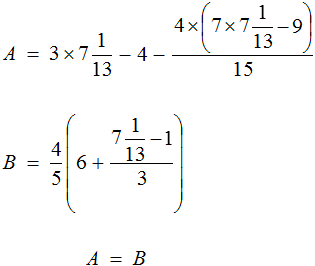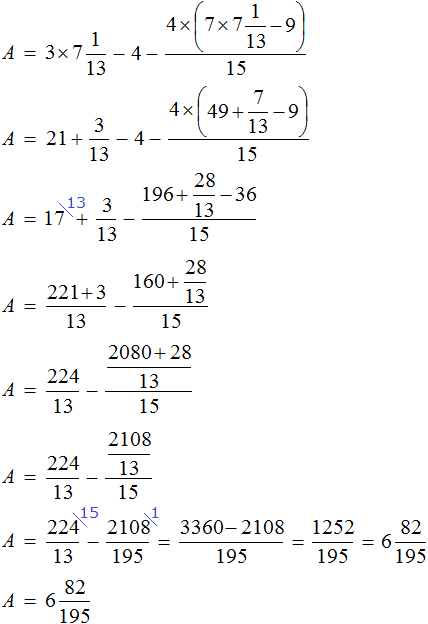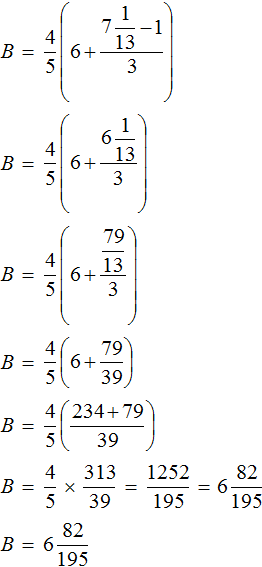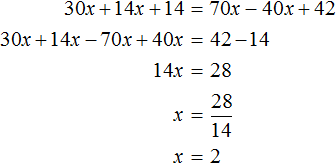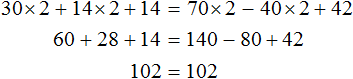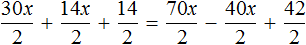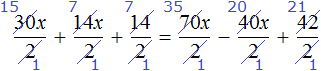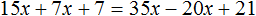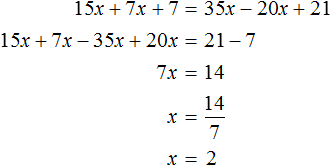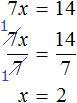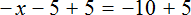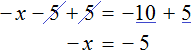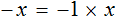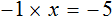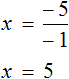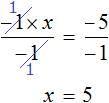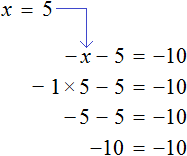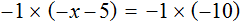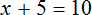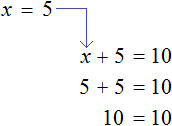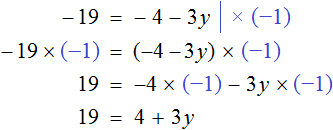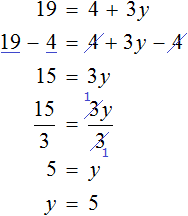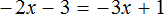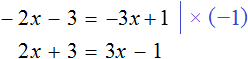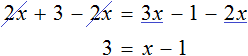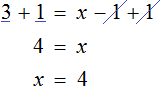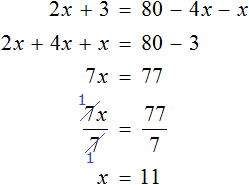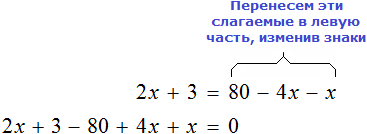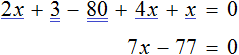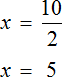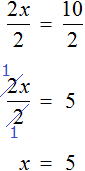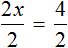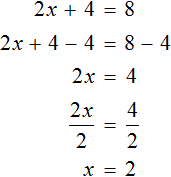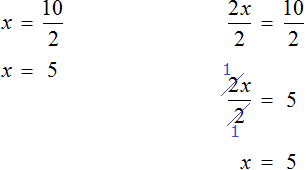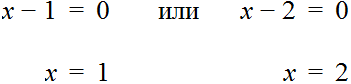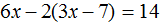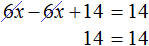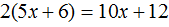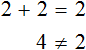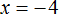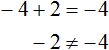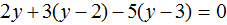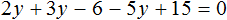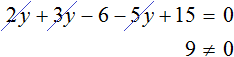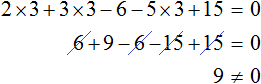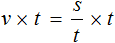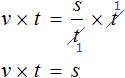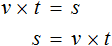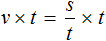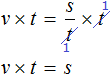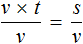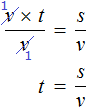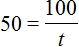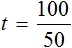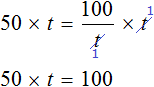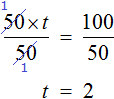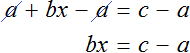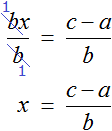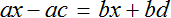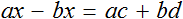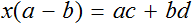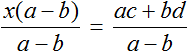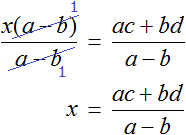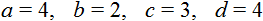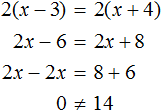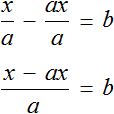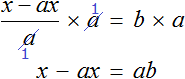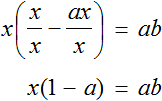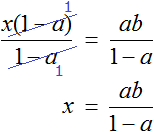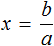Доказать что уравнение не имеет целых корней

Доказать что уравнение не имеет целых корней

Нам уже известны формулы для решения квадратных уравнений. А что делать, если встретится уравнение более высокой степени ? Оказы вается, что для уравнений третьей и четвёртой степени есть формулы, позволяющие найти корни (но они редко используются на практике ввиду их громоздкости), а для уравнений пятой степени и выше доказано, что таких формул не существует. Таким образом, у нас не выйдет в общем случае решить уравнение третьей или более высокой степени. Но существует ряд приёмов, позволяющих решить некоторые специальные виды уравнений. К их рассмотрению мы сейчас и перейдём.

Решите уравнение: `x^3 +4x^2 — 2x-3=0`.

Заметим, что `x=1` является корнем уравнения (значение многочлена при `x=1` равно сумме коэффициентов многочлена). Тогда по теореме Безу многочлен `x^3 +4x^2 -2x -3` делится на многочлен `x-1`. Выполнив деление, получаем:

`x^3 +4x^2 -2x -3=0 hArr (x-1)(x^2 + 5x +3) =0 hArr`

Обычно кубические уравнения решают именно так: подбирают один корень, выполняют деление уголком, после чего остаётся решить только квадратное уравнение. А что делать, если у нас уравнение четвёртой степени? Тогда придётся подбирать корень два раза. После подбора первого корня и деления останется кубическое уравнение, у которого надо будет подобрать ещё один корень. Возникает вопрос. Что делать, если такие «простые» числа как `+-1`, `+-2` не являются корнями уравне ния? Неужели тогда надо перебирать всевозможные числа? Ответ на этот вопрос даёт следующее утверждение.

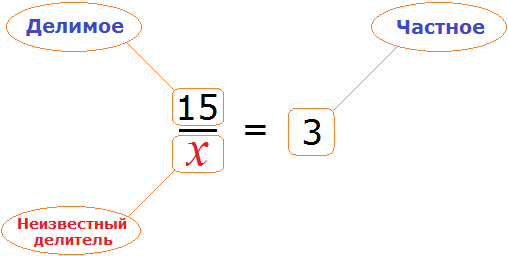
Если несократимая дробь `p//q` (`p` — целое, `q` — натуральное) является корнем многочлена с целыми коэффициентами , то сво бодный член делится на `p` , а старший коэффициент делится на `q`.

Пусть несократимая дробь `p//q` — корень многочлена (8). Это означает, что

`a_n (p/q)^n +a_(n-1)(p/q)^(n-1) + a_(n-2) (p/q)^(n-2)+ . «+a_2 (p/q)^2 +a_1(p/q)+0=0`.

Умножим обе части на `q^n`, получаем:

`a_n p^n + a_(n-1) p^(n-1) q+a_(n-2) p^(n-2) q^2 + . + a_2 p^2 q^(n-2) +a_1 pq^(n-1)+a_0q^n=0`.

Перенесём в правую часть, а из оставшихся слагаемых вынесем `p` за скобки:

Справа и слева в (14) записаны целые числа. Левая часть делится на `p=>` правая часть также делится на `p`. Числа `p` и `q` взаимно просты (т. к. дробь `p//q` несократимая), откуда следует, что `a_0 vdotsp`.

Аналогично доказывается, что `a_n vdotsq`. Теорема доказана.

Как правило, предлагаемые вам уравнения имеют целые корни, поэтому в большинстве задач используется следующее: если у многочлена с целыми коэффициентами есть целые корни, то они являются делителями свободного члена.

а) `x^4+4x^3-102x^2-644x-539=0`; (15)

б) `6x^4-35x^3+28x^2+51x+10=0`. (16)

а) Попробуем найти целые корни уравнения. Пусть `p` — корень. Тогда `539vdotsp`; чтобы найти возможные значения `p`, разложим число `539` на простые множители:

Поэтому `p` может принимать значения:

Подстановкой убеждаемся, что `x=-1` является корнем уравнения. Разделим многочлен в левой части (15) уголком на `x+1` и получим:

Далее подбираем корни у получившегося многочлена третьей степени. Получаем `x=-7`, а после деления на `(x+7)` остаётся `(x+1)(x+7)(x^2-4x-77)=0`. Решая квадратное уравнение, находим окончательное разложение левой части на множители:

1) После того, как найден первый корень, лучше сначала выполнить деление уголком, и только потом приступать к поиску последующих корней. Тогда вычислений будет меньше.

2) В разложении многочлена на множители множитель `(x+7)` встретился дважды. Тогда говорят, что `(–7)` является корнем кратности два. Аналогично говорят о корнях кратности три, четыре и т. д.

б) Если уравнение имеет рациональный корень `x_0=p/q`, то `10vdotsp`, `6vdotsq`, т. е. `p in<+-1;+-2;+-5;+-10>`; `qin<1;2;3;6>`.Возможные варианты для `x_0`:

Начинаем перебирать числа из этого списка. Первым подходит число `x=5/2`. Делим многочлен в левой части (16) на `(2x-5)` и получаем

Заметим, что для получившегося кубического уравнения выбор рациональных корней заметно сузился, а именно, следующие числа могут быть корнями: `x_0=+-1,+-2,+-1/3,+-2/3`, причём мы уже знаем, что числа `+-1` и `+-2` корнями не являются (так как мы их подставляли раньше, и они не подошли). Находим, что `x=-2/3` — корень; делим `3x^3-10x^2-11x-2` на `3x+2` и получаем:

Решаем квадратное уравнение: `x^2-4x-1=0 iff x=2+-sqrt5`.

К сожалению, уравнения не всегда имеют рациональные корни. Тогда приходится прибегать к другим методам.

Разложите на множители:

а) `x^4+4=x^4+4x^2+4-4x^2=(x^2+2)^2-(2x)^2=`

Таким образом, сумму четвёртых степеней, в отличие от суммы квадратов, можно разложить на множители:

в) Вынесем `x^2` за скобки и сгруппируем:

Обозначим `x+2/x=t`. Тогда `x^2+4+4/x^2=t^2`, `x^2+4/x^2=t^2-4`, выражение в скобках принимает вид:

В итоге получаем:

Этот приём иногда используется для решения уравнений четвёртой степени; в частности, с его помощью решают возвратные уравнения (см. пример 12 е).

г)* Можно убедиться, что никакой из рассмотренных выше методов не помогает решить задачу, а именно: рациональных корней уравнение не имеет (числа `+-1` и `+-2` – не корни); вынесение числа `x^2` за скобки и группировка слагаемых приводит к выражению

Если здесь обозначить `4x-13/x=t`, то `x^2-2/x^2` через `t` рационально не выражается.

Прибегнем к методу неопределённых коэффициентов. Пусть

Попробуем подобрать коэффициенты `a`, `b`, `c`, `d` так, чтобы (17) обратилось в верное равенство. Для этого раскроем скобки в правой части и приведём подобные слагаемые:

Приравняем в (18) коэффициенты при одинаковых степенях в обеих частях уравнения. Получим систему уравнений:

Мы будем пытаться найти целочисленные решения системы (19). Найти все решения системы (19) не проще, чем решить исходную задачу, однако нахождение целочисленных решений – разумеется, если они есть – нам по силам.

Рассмотрим четвёртое уравнение. Возможны только два принципиально различных случая:

2) `b=2` и `d=-1`. Рассмотрим каждый из них. Подставляем значения `b` и `d` в первые три уравнения:

Из первого и третьего уравнений системы получаем `c=5/3`; `a=-17/3`, что не удовлетворяет второму уравнению, поэтому система решений не имеет; пара чисел `b=1` и `d=-2` не подходит.

Эта система имеет одно решение `a=-7`, `c=3`. Значит, числа `a=-7`, `b=2`, `c=3`, `d=-1` являются решением системы (19), поэтому

Далее каждый из квадратных трёхчленов можно разложить на множители.

Во многих ситуациях степень уравнения можно понизить с помощью замены переменных.

Алгебра

План урока:

Целое уравнение и его степень

Ранее мы уже изучали понятие целого выражения. Так называют любое выражение с переменной, в котором могут использоваться любые арифметические операции, а также возведение в степень. Однако есть важное ограничение – в целом выражении переменная НЕ может находиться в знаменателе какой-нибудь дроби или быть частью делителя. Также переменная не может находиться под знаком корня. Для наглядности приведем примеры целых выражений:

(n 3 + 7)/5 (в знаменателе находится только число, без переменной);

А вот примеры нецелых выражений:

Отличительной особенностью целых выражений является то, что в них переменная может принимать любое значение. В нецелых же выражениях возникают ограничения на значения переменной, ведь знаменатель дроби не должен равняться нулю, в выражение под знаком корня не должно быть отрицательным.

Введем понятие целого уравнения.

Приведем примеры целых ур-ний:

0,75х 7 + 0,53х 6 – 45х = 18

Напомним, что в математике существует понятие равносильных уравнений.

Когда мы решаем ур-ния, мы в каждой новой строчке записываем ур-ние, равносильное предыдущему. Для этого используются равносильные преобразования (перенос слагаемых через знак «=» с противоположным знаком, деление обоих частей равенства на одинаковые числа и т. д.).

Можно доказать (мы этого делать не будем), что любое целое ур-ние можно возможно преобразовать так, чтобы получилось иное, равносильное ему ур-ние, где в левой части будет находиться многочлен, а справа – ноль. Для этого надо лишь раскрыть скобки и умножить ур-ние на какое-нибудь число, чтобы избавиться от дробей.

Пример. Преобразуйте целое ур-ние

так, чтобы слева стоял многочлен, а справа – ноль.

Решение. В ур-нии есть дроби со знаменателями 5 и 4. Если умножить обе части на 20 (это наименьшее общее кратное чисел 5 и 4), то дроби исчезнут:

Теперь раскроем скобки:

4(5х 3 – 3х 4 + 45х – 27х 2 ) – 40 = 10х 2 + 5х + 35

20х 3 – 12х 4 + 180х – 108х 2 – 40 = 10х 2 + 5х + 35

Осталось перенести все слагаемые влево и привести подобные слагаемые:

20х 3 – 12х 4 + 180х – 108х 2 – 40 – 10х 2 – 5х – 35 = 0

– 12х 4 + 20х 3 – 118х 2 + 175х – 75 = 0

Получили ур-ние в той форме, которую и надо было найти по условию.

Ответ:– 12х 4 + 20х 3 – 118х 2 + 175х – 75 = 0

В математике любой полином можно обозначить как Р(х). Если ур-ние привели к тому виду, когда в одной части многочлен, а в другой ноль, то говорят, что получили ур-ние вида Р(х) = 0.

Получается, что решение целого уравнения всегда можно свести к решению равносильного ему ур-ния Р(х) = 0. Именно поэтому многочлены играют такую большую роль в математике

Напомним, что степенью многочлена называется максимальная степень входящего в его состав одночлена. Это же число является и степенью целого уравнения Р(х) = 0, а также степенью любого равносильного ему целого ур-ния.

Пример. Определите степень ур-ния

(х 3 – 5)(2х + 7) = 2х 4 + 9

Решение. Приведем ур-ние к виду Р(х) = 0. Для этого раскроем скобки:

(х 3 – 5)(2х + 7) = 2х 4 + 9

2х 4 + 7х 3 – 10х – 35 = 2х 4 + 9

Перенесем все слагаемые влево и приведем подобные слагаемые:

2х 4 + 7х 3 – 10х – 35 – 2х 4 – 9 = 0

7х 3 – 10х – 44 = 0

Получили в левой части многочлен 3-ей степени. Следовательно, и исходное ур-ние имело такую же степень

Приведем примеры ур-ний первой степени:

5,4568у + 0,0002145 = 0

Все они являются линейными ур-ниями, метод их решения изучался ранее. Они имеют 1 корень.

Приведем примеры ур-ний второй степени:

6t 2 + 98t – 52 = 0

Это квадратные ур-ния. У них не более двух действительных корней. Для их нахождения в общем случае надо вычислить дискриминант и использовать формулу

Квадратные и линейные ур-ния умели решать ещё в Древнем Вавилоне 4 тысячи лет назад! А вот с ур-ния 3-ей степени (их ещё называют кубическими уравнениями) оказались значительно сложнее. Приведем их примеры:

2х 3 + 4х 2 – 19х + 17 = 0

Лишь в 1545 году итальянец Джералимо Кардано опубликовал книгу, в которой описывался общий алгоритм решения кубических ур-ний. Он достаточно сложный и не входит в школьный курс математики. Его ученик, Лодовико Феррари, предложил метод решения ур-ний четвертой степени. В качестве примера такого ур-ния можно привести:

5х 4 + 6х 3 – 2х 2 – 10х + 1 = 0

Лишь в XIX веке было доказано, что для ур-ний более высоких степеней (5-ой, 6-ой и т. д.) не существует универсальных формул, с помощью которых можно было бы найти их корни.

Отметим, что если степень целого ур-ния равна n, то у него не более n корней (но их число может быть и меньше). Так, количество корней кубического уравнения не превышает трех, а у ур-ния 4-ой степени их не более 4.

Чтобы доказать это утверждение, сначала покажем способ составления уравнения Р(х) = 0, имеющего заранее заданные корни. Пусть требуется составить ур-ние, имеющее корни k₁, k₂,k₃,…k_n. Приравняем к нулю следующее произведение скобок:

Составленное ур-ние имеет все требуемые корни и никаких других корней. Действительно, произведение множителей может равняться нулю только в случае, если хотя бы один из множителей нулевой. Поэтому для решения ур-ния

надо каждую скобку приравнять к нулю:

х – k₁ = 0 или х – k₂ = 0 или х – k₃ = 0 или…х – k_n = 0

Перенесем второе слагаемое вправо в каждом равенстве и получим:

Чтобы вместо произведения скобок слева стоял многочлен, надо просто раскрыть скобки.

Пример. Составьте уравнение в виде Р(х) = 0, имеющее корни 1, 2, 3 и 4.

Запишем целое ур-ние, имеющее требуемые корни:

(х – 1)(х – 2)(х – 3)(х – 4) = 0

Будем поочередно раскрывать скобки, умножая 1-ую скобку на 2-ую, полученный результат на 3-ю и т.д.:

(х 2 – 3х + 2)(х – 3)(х – 4) = 0

(х 3 – 6х 2 + 11х – 6)(х – 4) = 0

х 4 – 10х 3 + 35х 2 – 50х +24 = 0

Получили ур-ние вида Р(х) = 0. Для проверки вычислений можно подставить в него числа 1, 2, 3 и 4 и убедиться, что они обращают ур-ние в верное равенство.

Ответ: х 4 – 10х 3 + 35х 2 – 50х +24 = 0

Заметим, что в рассмотренном примере, когда мы перемножали многочлены, мы получали новый полином, чья степень увеличивалась на единицу. Мы перемножили 4 скобки (х – k₁), а потому получили полином 4 степени. Если бы мы перемножали, скажем, 10 таких скобок, то и многочлен бы получился 10-ой степени. Именно поэтому ур-ние n-ой степени не более n корней.

Действительно, предположим, что какое-то ур-ние n-ой степени имеет хотя бы (n + 1) корень. Обозначим эти корни как k₁, k₂,k₃,…k_n, k_n+1 и запишем уравнение:

Оно, по определению, равносильно исходному ур-нию, ведь оно имеет тот же набор корней. Слева записаны (n + 1) скобок, поэтому при их раскрытии мы получим полином степени (n + 1). Значит, и исходное ур-ние на самом деле имеет степень n + 1, а не n. Получили противоречие, которое означает, что на самом деле у уравнения n-ой степени не более n корней.

Особо акцентируем внимание на том факте, что если корнями уравнения являются некоторые числа k₁, k₂,k₃,…k_n, то этому ур-нию равносильна запись (х – k₁)(х – k₂)(х – k₃)…(х – k_n) = 0

Этот факт будет использован далее при решении ур-ний.

Решение уравнений методом подбора корня

Необязательно преобразовывать ур-ние, чтобы найти его корни. Одним из приемов решения целых уравнений является метод подбора корня. Ведь если надо доказать, что какое-то число – это корень ур-ния, достаточно просто подставить это число в ур-ние и получить справедливое равенство!

Пример. Докажите, что корнями ур-ния

х 3 – 2х 2 – х + 2 = 0

являются только числа (– 1), 1 и 2.

Решение. Подставим в ур-ние каждую из предполагаемых корней и получим справедливое равенство. При х = – 1 имеем:

(– 1) 3 – 2(– 1) 2 – (– 1) + 2 = 0

При х = 1 получаем:

1 3 – 2•1 2 – 1 + 2 = 0

Наконец, рассмотрим случай, когда х = 2

2 3 – 2•2 2 – 2 + 2 = 0

Исходное ур-ние имеет 3-ю степень, поэтому у него не более 3 корней. То есть других корней, кроме (– 1), 1 и 2 , у него нет.

Конечно, просто так подобрать корни довольно тяжело. Однако есть некоторые правила, которые помогают в этом. Для начала введем понятие коэффициентов уравнения.

Понятно, что ур-ние Р(х) = 0 в общем виде можно записать так:

Числа а₀, а₁, а₂,…а_nи называют коэффициентами уравнений.

Например, для уравнения

5х 4 – 7х 3 + 9х 2 – х + 12 = 0

Если одна из слагаемых «пропущено» в уравнении, то считают, что коэффициент перед ним равен нулю. Например, в ур-нии

нет слагаемого с буквенной частью х 2 . Можно считать, что ур-ние равносильно записи

х 3 + 0х 2 + 2х – 15 = 0

где слагаемое х 2 есть, но перед ним стоит ноль. Тогда коэффициент а₁ = 0.

Для обозначения первого коэффициента а₀ может использоваться термин старший коэффициент, а для последнего коэффициента а_n – термин «свободный член» или «свободный коэффициент».

Изучение коэффициентов ур-ния помогает быстрее подобрать корень. Существует следующая теорема:

Докажем это утверждение. Пусть m – это целый корень уравнения с целыми коэффициентами

Тогда можно подставить туда число m и получить верное равенство:

Поделим обе его части на m и получим

Справа – целое число (ноль), значит, и сумма чисел слева также целая. Все числа а₀m n –1 , a₁m n –2 , а_n–1, очевидно, целые (так как и целыми являются и m, и все коэффициенты). Значит, и число а_n/m должно быть целым. Но это возможно лишь в том случае, если m является делителем числа а_n.

Из доказанной теоремы следует, что при подборе корней ур-ния достаточно рассматривать только те из них, которые являются делителями свободного члена. При этом следует учитывать и отрицательные делители.

Пример. Найдите целые корни уравнения

2х 4 – х 3 – 9х 2 + 4х + 4 = 0

Решение. Все коэффициенты ур-ния – целые, а потому целый корень должен быть делителем свободного члена, то есть числа 4. Делителями четверки являются 1 и (– 1), 2 и (– 2), 4 и (– 4). Подставляя каждое из этих чисел в ур-ние, получим верные равенства только для чисел 1, 2 и (– 2):

2•1 4 – 1 3 – 9•1 2 + 4•1 + 4 = 2 – 1 – 9 + 4 + 4 = 0

2•2 4 – 2 3 – 9•2 2 + 4•2 + 4 = 32 – 8 – 36 + 8 + 4 = 0

2•(– 2) 4 – (– 2) 3 – 9•(– 2) 2 + 4(– 2) + 4 = 32 + 8 – 36 – 8 + 4 = 0

Таким образом, только эти числа и могут быть целыми корнями ур-ния. Так как мы рассматриваем ур-ние 4 степени, то, возможно, у него помимо 3 целых корней есть ещё один дробный.

Пример. Решите ур-ние

0,5х 3 + 0,5х + 5 = 0

Решение. У ур-ния дробные коэффициенты. Умножим обе части равенства на 2 и получим ур-ние с целыми коэффициентами:

0,5х 3 + 0,5х + 5 = 0

(0,5х 3 + 0,5х + 5)•2 = 0•2

Попытаемся подобрать целый корень ур-ния. Он должен быть делителем свободного члена, то есть десятки. Возможными кандидатами являются числа 1 и (– 1), 2 и (– 2), 5 и (– 5), 10 и (– 10). Подходит только корень х = – 2:

(– 2) 3 + (– 2) + 10 = – 8 – 2 + 10 = 0

Обратим внимание, что в левой части ур-ния стоит сумма функций, возрастающих на всей числовой прямой: у = х 3 и у = х + 10. Значит, и вся левая часть х 3 + х + 10 монотонно возрастает. Это значит, что у ур-ния есть только один корень, и мы его нашли ранее подбором.

Ещё быстрее можно узнать, является ли единица корнем уравнения.

Докажем это. Подставим в ур-ние

значение х = 1. Так как единица в любой степени равна самой единице, то получим:

Получили равенство, в котором слева стоит сумма коэффициентов, в справа – ноль. Если сумма коэффициентов действительно равна нулю, то равенство верное, а, значит, единица является корнем ур-ния.

Пример. Укажите хотя бы 1 корень ур-ния

499х 10 – 9990х 7 + 501х 6 – 10х 5 + 10000х 4 – 1000 = 0

Решение. Заметим, что при сложении коэффициентов ур-ния получается 0:

499 – 9990 + 501 – 10 + 10000 – 1000 = (499 + 501 – 1000) + (10000 – 9990 – 10) = 0 + 0 = 0

Следовательно, единица является его корнем.

Решение уравнений с помощью разложения многочлена на множители

Если в уравнении вида P(x) = 0в левой части удается выполнить разложение многочлена на множители, то дальше каждый из множителей можно отдельно приравнять к нулю.

Пример. Решите ур-ние

Решение. Степень х 4 можно представить как (х 2 ) 2 , а 16 – как 4 2 . Получается, что слева стоит разность квадратов, которую можно разложить на множители по известной формуле:

(х 2 – 4)(х 2 + 4) = 0

Приравняем каждую скобку к нулю и получим два квадратных ур-ния:

х 2 – 4 = 0 или х 2 + 4 = 0

х 2 = 4 или х 2 = – 4

Первое ур-ние имеет два противоположных корня: 2 и (– 2). Второе ур-ние корней не имеет.

Предположим, что у ур-ния 3-ей степени есть 3 корня, и подбором мы нашли один из них. Как найти оставшиеся корни? Здесь помогает процедура, известная как «деление многочленов в столбик». Продемонстрируем ее на примере. Пусть надо решить ур-ние

100х 3 – 210х 2 + 134х – 24 = 0

Можно заметить, сумма всех коэффициентов ур-ния равна нулю:

100 – 210 + 134 – 24 = 0

Следовательно, первый корень – это 1.

Предположим, что у исходного ур-нияР(х) = 0 есть 3 корня, k₁, k₂и k₃. Тогда ему равносильно другое ур-ние

Мы нашли, что первый корень k₁ = 1, то есть

Обозначим как P₁(x) = 0 ещё одно ур-ние, корнями которого будут только числа k₂ и k₃. Очевидно, что корнями ур-ния

Будут числа 1, k₂ и k₃. Его корни совпадают с корнями исходного ур-ния, а потому запишем

(х – 1)•P₁(x) = 100х 3 – 210х 2 + 134х – 24

Поделим обе части на (х – 1):

Итак, если «поделить» исходное ур-ние на х – 1, то получим какой-то многочлен Р₁(х), причем решением уравнения P₁(x) = 0 будут оставшиеся два корня, k₂и k₃. Деление можно выполнить в столбик. Для этого сначала запишем «делимое» и «делитель», как и при делении чисел:

Смотрим на первое слагаемое делимого. Это 100х 3 . На какой одночлен нужно умножить делитель (х – 1), чтобы получился полином со слагаемым 100х 3 ? Это 100х 2 . Действительно, (х – 1)100х 2 = 100х 3 – 100х 2 . Запишем слагаемое 100х 2 в результат деления, а результат его умножения на делитель, то есть 100х 3 – 100х 2 , вычтем из делимого:

Теперь вычтем из делимого то выражение, которое мы записали под ним. Слагаемые 100х 3 , естественно, сократятся:

(100х 3 – 210х 2 ) – (100х 3 – 100х 2 ) = 100х 3 – 210х 2 – 100х 3 + 100х 2 = – 110х 2

Далее снесем слагаемое 134х вниз:

На какое слагаемое нужно умножить (х – 1), что получился полином со слагаемым (– 110х 2 ). Очевидно, на (– 110х):

(х – 1)(– 110х 2 ) = –110х 2 + 110х

Запишем в поле «ответа» слагаемое (– 110х 2 ), а под делимый многочлен – результат его умножения на (х – 1):

При вычитании из (–110х 2 + 134х) полинома (–110х 2 + 110х) остается 24х. Далее сносим последнее слагаемое делимого многочлена вниз:

Выражение х – 1 нужно умножить на 24, чтобы получить 24х – 24. Запишем в поле «ответа» число 24, а в столбике произведение 24(х –1) = 24х – 24:

В результате в остатке получился ноль. Значит, всё сделано правильно. С помощью деления столбиком мы смогли разложить полином 100х 3 – 210х 2 + 134х – 24 на множители:

100х 3 – 210х 2 + 134х – 24 = (х – 1)(100х 2 – 110х + 24)

Теперь перепишем исходное ур-ние с учетом этого разложения:

100х 3 – 210х 2 + 134х – 24 = 0

(х – 1)(100х 2 – 110х + 24) = 0

Теперь каждую отдельную скобку можно приравнять нулю. Получим ур-ние х – 1 = 0, корень которого, равный единице, мы уже нашли подбором. Приравняв к нулю вторую скобку, получим квадратное ур-ние:

100х 2 – 110х + 24 = 0

D =b 2 – 4ас = (– 110) 2 – 4•100•24 = 12100 – 9600 = 2500

Итак, мы нашли три корня ур-ния: 1; 0,3 и 0,8.

В данном случае мы воспользовались следующим правилом:

Пример. Решите уравнение

2х 3 – 8х 2 + 16 = 0

Решение. Все коэффициенты целые, а потому, если у уравнения есть целый корень, то он должен быть делителем 16. Перечислим эти делители: 1, – 1, 2, – 2, 4, – 4, 8, – 8, 16, – 16. Из всех них подходит только двойка:

2•2 3 – 8•2 2 + 16 = 16 – 32 + 16 = 0

Итак, первый корень равен 2. Это значит, что исходный многочлен можно разложить на множители, один из которых – это (х – 2). Второй множитель найдем делением в столбик. Так как в многочлене 2х 3 – 8х 2 + 16 нет слагаемого с буквенной часть х, то искусственно добавим её:

2х 3 – 8х 2 + 16 = 2х 3 – 8х 2 + 0х + 16

Теперь возможно деление:

Получили, что 2х 3 – 8х 2 + 16 = (х – 2)(2х – 4х – 8)

С учетом этого перепишем исходное ур-ние:

2х 3 – 8х 2 + 16 = 0

(х – 2)(2х – 4х – 8) = 0

х – 2 = 0 или 2х – 4х – 8 = 0

Решим квадратное ур-ние

D =b 2 – 4ас = (– 4) 2 – 4•2•(– 8) = 16 + 64 = 80

В 8 классе мы узнали, что если у квадратного ур-ния ах 2 + bx + c = 0 есть два корня, то многочлен ах 2 + bx + c можно разложить на множители по формуле

где k₁ и k₂– корни квадратного ур-ния. Оказывается, такое же действие можно выполнять с многочленами и более высоких степеней. В частности, если у кубического ур-ния есть 3 корня k₁, k₂ и k₃, то его можно разложить на множители по формуле

Пример. Разложите на множители многочлен 2х 3 – 4х 2 – 2х + 4.

Решение. Целые корни этого многочлена (если они есть), должны быть делителем четверки. Из всех таких делителей подходят три: 1, (– 1) и 2:

2•1 3 – 4•1 2 – 2•1 + 4 = 2 – 4 – 2 + 4 = 0

2•(– 1) 3 – 4•(– 1) 2 – 2•(– 1) + 4 = – 2 – 4 + 2 + 4 = 0

2•2 3 – 4•2 2 – 2•2 + 4 = 16 – 16 – 4 + 4 = 0

Значит, многочлен можно разложить на множители:

2х 3 – 4х 2 – 2х + 4 = 2(х + 1)(х – 1)(х – 2)

Возникает вопрос – почему перед скобками нужна двойка? Попробуем сначала перемножить скобки без ее использования:

(х + 1)(х – 1)(х – 2) = (х 2 – 1)(х – 2) = х 3 – 2х 2 – х + 2

Получили не тот многочлен, который стоит в условии. Однако ур-ние

х 3 – 2х 2 – х + 2 = 0

имеет те же корни (1, 2 и (– 1)), что и ур-ние

2х 3 – 4х 2 – 2х + 4 = 0

Дело в том, что это равносильные ур-ния, причем второе получено умножением первого на два:

2•(х 3 – 2х 2 – х + 2) = 2х 3 – 4х 2 – 2х + 4

Надо понимать, что хотя ур-ния 2х 3 – 4х 2 – 2х + 4 = 0 и х 3 – 2х 2 – х + 2 = 0, по сути, одинаковы, многочлены в их левой части различны. Заметим, что при перемножении скобок (х – k₁), (х – k₂), (х – k₃) и т.д. всегда будет получаться полином, у которого старший коэффициент равен единице. Поэтому, чтобы учесть этот самый коэффициент, надо домножить произведение скобок на него:

2х 3 – 4х 2 – 2х + 4= 2•(х 3 – 2х 2 – х + 2) = 2(х + 1)(х – 1)(х – 2)

Ответ: 2(х + 1)(х – 1)(х – 2).

Графический метод решения уравнений

Любое ур-ние с одной переменной можно представить в виде равенства

где у(х) и g(x) – некоторые функции от аргумента х.

Построив графики этих функций, можно примерно найти точки их пересечений. Они и будут соответствовать корням уравнения.

Пример. Решите графически уравнение

Решение. Строить график уравнения х 3 – х 2 – 1 = 0 довольно сложно, поэтому перенесем слагаемое (– х 2 – 1) вправо:

Построим графики у = х 3 и у = х 2 + 1 (второй можно получить переносом параболы у = х 2 на единицу вверх):

Видно, они пересекаются в точке, примерно соответствующей значению х ≈ 1,4. Если построить графики уравнения более точно (с помощью компьютера), то можно найти, что х ≈ 1,46557.

Ответ: х ≈ 1,46557

Конечно, графический метод решения уравнений не является абсолютно точным, однако он помогает быстро найти примерное положение корня. Также с его помощью можно определить количество корней уравнения. В рассмотренном примере был только 1 корень.

Пример. Определите количество корней уравнений

б) х 3 – 2х + 0,5 = 0

Решение. Перенесем два последних слагаемых вправо в каждом ур-нии:

Построим графики функций у = х 3 , у = х + 3 и у = 2х – 0,5:

Видно, что прямая у = х + 3 пересекает график у = х 3 в одной точке, поэтому у первого ур-ния будет 1 решение.Прямая у = 2х – 0,5 пересекает кубическую параболу в трех точках, а потому у второго ур-ния 3 корня.

Ответ: а) один корень; б) три корня.

Решение дробно-рациональных уравнений

До этого мы рассматривали только целые ур-ния, где переменная НЕ находится в знаменателе какого-нибудь выражения. Однако, если в ур-нии есть выр-ние, содержащее переменную в знаменателе, или присутствует деление на выр-ние с переменной, то его называют дробно-рациональным уравнением.

Приведем несколько примеров ур-ний, считающихся дробно-рациональными:

С помощью равносильных преобразований любое дробно-рациональное ур-ние возможно записать в виде отношения двух полиномов:

Дробь равна нулю лишь тогда, когда ее числитель равен нулю, а знаменатель – не равен. Таким образом, нужно сначала решить ур-ние Р(х) = 0 и потом проверить, что полученные корни не обращают полином Q(x) в ноль.

Обычно для решения дробно-рациональных уравнений используют такой алгоритм:

1) Приводят все дроби к единому знаменателю, умножают на него ур-ние и получают целое ур-ние.

2) Решают полученное целое ур-ние.

3) Исключают из числа корней те, которые обращают знаменатель хотя бы одной из дробей в ноль.

Пример. Решите ур-ние

Умножим обе части равенства на знаменатель 1-ой дроби:

2х 2 – 3х – 2 = х 2 (х – 2)

Раскроем скобки и перенесем все слагаемые в одну сторону:

2х 2 – 3х – 2 = х 3 – 2х 2

х 3 – 2х 2 – 2х 2 + 3х + 2 = 0

х 3 – 4х 2 + 3х + 2 = 0

У ур-ния могут быть только те целые корни, которые являются делителями двойки. Из кандидатов 1, – 1, 2 и – 2 подходит только двойка:

2 3 – 4•2 2 + 3•2 + 2 = 8 – 16 + 6 + 2 = 0

Нашли один корень, а потому исходный многочлен можно поделить в столбик на (х – 2):

Получили, что х 3 – 4х 2 + 3х + 2 = (х – 2)(х 2 – 2х – 1)

Тогда ур-ние примет вид:

(х – 2)(х 2 – 2х – 1) = 0

х – 2 = 0 или х 2 – 2х – 1 = 0

Решим квадратное ур-ние:

D =b 2 – 4ас = (– 2) 2 – 4•1•(– 1) = 4 + 4 = 8

Мы нашли все 3 корня кубического ур-ния. Теперь надо проверить, не обращают ли какие-нибудь из них знаменатели дроби в исходном ур-нии

в ноль. Очевидно, что при х = 2 знаменатель (х – 2) превратится в ноль:

Это значит, что этот корень надо исключить из списка решений. Такой корень называют посторонним корнем ур-ния.

Также ясно, что два остальных корня не обращают знаменатель в ноль, а потому они НЕ должны быть исключены из ответа:

Пример. Найдите все корни ур-ния

Решение. Если сразу привести выражение слева к общему знаменателю 4(х 2 + х – 2)(х 2 + х – 20), то получится очень длинное и неудобное выражение. Однако знаменатели довольно схожи, поэтому можно провести замену. Обозначим х 2 + х как у:

Тогда уравнение примет вид

Приведем дроби к общему знаменателю 4(у – 2)(у – 20):

Знаменатель должен равняться нулю:

4(у – 20) + 28(у – 2) + (у – 2)(у – 20) = 0

4у – 80 + 28у – 56 + у 2 – 20у – 2у + 40 = 0

у 2 + 10у – 96 = 0

Решаем квадратное ур-ние:

D =b 2 – 4ас = (10) 2 – 4•1•(– 96) = 100 + 384 = 484

Получили, что у₁ = – 16, а у₂ = 6. Произведем обратную замену:

х 2 + х = – 16 или х 2 + х = 6

х 2 + х + 16 = 0 или х 2 + х – 6 = 0

Дискриминант 1-ого ур-ния отрицателен:

D =b 2 – 4ас = (1) 2 – 4•1•(16) = 1– 64 = – 63

А потому оно не имеет решений. Решим 2-ое ур-ние:

D = b 2 – 4ас = (1) 2 – 4•1•(– 6) = 1+ 24 = 25

Нашли два корня: 2 и (– 3). Осталось проверить, не обращают ли они знаменатели дробей в ур-нии

в ноль. Подстановкой можно убедиться, что не обращают.

При решении дробно-рациональных ур-ний может использоваться и графический метод.

Пример. Сколько корней имеет уравнение

Решение. Построим графики функций у = х 2 – 4 и у = 2/х:

Видно, что графики пересекаются в 3 точках, поэтому ур-ние имеет 3 корня.

Общие сведения об уравнениях

Уравнения — одна из сложных тем для усвоения, но при этом они являются достаточно мощным инструментом для решения большинства задач.

С помощью уравнений описываются различные процессы, протекающие в природе. Уравнения широко применяются в других науках: в экономике, физике, биологии и химии.

В данном уроке мы попробуем понять суть простейших уравнений, научимся выражать неизвестные и решим несколько уравнений. По мере усвоения новых материалов, уравнения будут усложняться, поэтому понять основы очень важно.

Что такое уравнение?

Уравнение — это равенство, содержащее в себе переменную, значение которой требуется найти. Это значение должно быть таким, чтобы при его подстановке в исходное уравнение получалось верное числовое равенство.

Например выражение 3 + 2 = 5 является равенством. При вычислении левой части получается верное числовое равенство 5 = 5 .

А вот равенство 3 + x = 5 является уравнением, поскольку содержит в себе переменную x , значение которой можно найти. Значение должно быть таким, чтобы при подстановке этого значения в исходное уравнение, получилось верное числовое равенство.

Другими словами, мы должны найти такое значение, при котором знак равенства оправдал бы свое местоположение — левая часть должна быть равна правой части.

Уравнение 3 + x = 5 является элементарным. Значение переменной x равно числу 2. При любом другом значении равенство соблюдáться не будет

Говорят, что число 2 является корнем или решением уравнения 3 + x = 5

Корень или решение уравнения — это значение переменной, при котором уравнение обращается в верное числовое равенство.

Корней может быть несколько или не быть совсем. Решить уравнение означает найти его корни или доказать, что корней нет.

Переменную, входящую в уравнение, иначе называют неизвестным. Вы вправе называть как вам удобнее. Это синонимы.

Примечание. Словосочетание «решить уравнение» говорит самó за себя. Решить уравнение означает «уравнять» равенство — сделать его сбалансированным, чтобы левая часть равнялась правой части.

Выразить одно через другое

Изучение уравнений по традиции начинается с того, чтобы научиться выражать одно число, входящее в равенство, через ряд других. Давайте не будем нарушать эту традицию и поступим также.

Рассмотрим следующее выражение:

Данное выражение является суммой чисел 8 и 2. Значение данного выражения равно 10

Получили равенство. Теперь можно выразить любое число из этого равенства через другие числа, входящие в это же равенство. К примеру, выразим число 2.

Чтобы выразить число 2, нужно задать вопрос: «что нужно сделать с числами 10 и 8, чтобы получить число 2». Понятно, что для получения числа 2, нужно из числа 10 вычесть число 8.

Так и делаем. Записываем число 2 и через знак равенства говорим, что для получения этого числа 2 мы из числа 10 вычли число 8:

Мы выразили число 2 из равенства 8 + 2 = 10 . Как видно из примера, ничего сложного в этом нет.

При решении уравнений, в частности при выражении одного числа через другие, знак равенства удобно заменять на слово «есть». Делать это нужно мысленно, а не в самом выражении.

Так, выражая число 2 из равенства 8 + 2 = 10 мы получили равенство 2 = 10 − 8 . Данное равенство можно прочесть так:

2 есть 10 − 8

То есть знак = заменен на слово «есть». Более того, равенство 2 = 10 − 8 можно перевести с математического языка на полноценный человеческий язык. Тогда его можно будет прочитать следующим образом:

Число 2 есть разность числа 10 и числа 8

Число 2 есть разница между числом 10 и числом 8.

Но мы ограничимся лишь заменой знака равенства на слово «есть», и то будем делать это не всегда. Элементарные выражения можно понимать и без перевода математического языка на язык человеческий.

Вернём получившееся равенство 2 = 10 − 8 в первоначальное состояние:

Выразим в этот раз число 8. Что нужно сделать с остальными числами, чтобы получить число 8? Верно, нужно из числа 10 вычесть число 2

Вернем получившееся равенство 8 = 10 − 2 в первоначальное состояние:

В этот раз выразим число 10. Но оказывается, что десятку выражать не нужно, поскольку она уже выражена. Достаточно поменять местами левую и правую часть, тогда получится то, что нам нужно:

Пример 2. Рассмотрим равенство 8 − 2 = 6

Выразим из этого равенства число 8. Чтобы выразить число 8 остальные два числа нужно сложить:

Вернем получившееся равенство 8 = 6 + 2 в первоначальное состояние:

Выразим из этого равенства число 2. Чтобы выразить число 2, нужно из 8 вычесть 6

Пример 3. Рассмотрим равенство 3 × 2 = 6

Выразим число 3. Чтобы выразить число 3, нужно 6 разделить 2

Вернем получившееся равенство 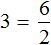в первоначальное состояние:

Выразим из этого равенства число 2. Чтобы выразить число 2, нужно 6 разделить 3

Пример 4. Рассмотрим равенство

Выразим из этого равенства число 15. Чтобы выразить число 15, нужно перемножить числа 3 и 5

Вернем получившееся равенство 15 = 3 × 5 в первоначальное состояние:

Выразим из этого равенства число 5. Чтобы выразить число 5, нужно 15 разделить 3

Правила нахождения неизвестных

Рассмотрим несколько правил нахождения неизвестных. Возможно, они вам знакомы, но не мешает повторить их ещё раз. В дальнейшем их можно будет забыть, поскольку мы научимся решать уравнения, не применяя эти правила.

Вернемся к первому примеру, который мы рассматривали в предыдущей теме, где в равенстве 8 + 2 = 10 требовалось выразить число 2.

В равенстве 8 + 2 = 10 числа 8 и 2 являются слагаемыми, а число 10 — суммой.

Чтобы выразить число 2, мы поступили следующим образом:

То есть из суммы 10 вычли слагаемое 8.

Теперь представим, что в равенстве 8 + 2 = 10 вместо числа 2 располагается переменная x

В этом случае равенство 8 + 2 = 10 превращается в уравнение 8 + x = 10 , а переменная x берет на себя роль так называемого неизвестного слагаемого

Наша задача найти это неизвестное слагаемое, то есть решить уравнение 8 + x = 10 . Для нахождения неизвестного слагаемого предусмотрено следующее правило:

Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.

Что мы в принципе и сделали, когда выражали двойку в равенстве 8 + 2 = 10 . Чтобы выразить слагаемое 2, мы из суммы 10 вычли другое слагаемое 8

А сейчас, чтобы найти неизвестное слагаемое x , мы должны из суммы 10 вычесть известное слагаемое 8:

Если вычислить правую часть получившегося равенства, то можно узнать чему равна переменная x

Мы решили уравнение. Значение переменной x равно 2 . Для проверки значение переменной x отправляют в исходное уравнение 8 + x = 10 и подставляют вместо x. Так желательно поступать с любым решённым уравнением, поскольку нельзя быть точно уверенным, что уравнение решено правильно:

В результате получается верное числовое равенство. Значит уравнение решено правильно.

Это же правило действовало бы в случае, если неизвестным слагаемым было бы первое число 8.

В этом уравнении x — это неизвестное слагаемое, 2 — известное слагаемое, 10 — сумма. Чтобы найти неизвестное слагаемое x , нужно из суммы 10 вычесть известное слагаемое 2

Вернемся ко второму примеру из предыдущей темы, где в равенстве 8 − 2 = 6 требовалось выразить число 8.

В равенстве 8 − 2 = 6 число 8 это уменьшаемое, число 2 — вычитаемое, число 6 — разность

Чтобы выразить число 8, мы поступили следующим образом:

То есть сложили разность 6 и вычитаемое 2.

Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 8 располагается переменная x

В этом случае переменная x берет на себя роль так называемого неизвестного уменьшаемого

Для нахождения неизвестного уменьшаемого предусмотрено следующее правило:

Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое.

Что мы и сделали, когда выражали число 8 в равенстве 8 − 2 = 6 . Чтобы выразить уменьшаемое 8, мы к разности 6 прибавили вычитаемое 2.

А сейчас, чтобы найти неизвестное уменьшаемое x , мы должны к разности 6 прибавить вычитаемое 2

Если вычислить правую часть, то можно узнать чему равна переменная x

Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 2 располагается переменная x

В этом случае переменная x берет на себя роль неизвестного вычитаемого

Для нахождения неизвестного вычитаемого предусмотрено следующее правило:

Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.

Что мы и сделали, когда выражали число 2 в равенстве 8 − 2 = 6. Чтобы выразить число 2, мы из уменьшаемого 8 вычли разность 6.

А сейчас, чтобы найти неизвестное вычитаемое x, нужно опять же из уменьшаемого 8 вычесть разность 6

Вычисляем правую часть и находим значение x

Вернемся к третьему примеру из предыдущей темы, где в равенстве 3 × 2 = 6 мы пробовали выразить число 3.

В равенстве 3 × 2 = 6 число 3 — это множимое, число 2 — множитель, число 6 — произведение

Чтобы выразить число 3 мы поступили следующим образом:

То есть разделили произведение 6 на множитель 2.

Теперь представим, что в равенстве 3 × 2 = 6 вместо числа 3 располагается переменная x

В этом случае переменная x берет на себя роль неизвестного множимого.

Для нахождения неизвестного множимого предусмотрено следующее правило:

Чтобы найти неизвестное множимое, нужно произведение разделить на множитель.

Что мы и сделали, когда выражали число 3 из равенства 3 × 2 = 6 . Произведение 6 мы разделили на множитель 2.

А сейчас для нахождения неизвестного множимого x , нужно произведение 6 разделить на множитель 2.

Вычисление правой части позволяет нам найти значение переменной x

Это же правило применимо в случае, если переменная x располагается вместо множителя, а не множимого. Представим, что в равенстве 3 × 2 = 6 вместо числа 2 располагается переменная x .

В этом случае переменная x берет на себя роль неизвестного множителя. Для нахождения неизвестного множителя предусмотрено такое же, что и для нахождения неизвестного множимого, а именно деление произведения на известный множитель:

Чтобы найти неизвестный множитель, нужно произведение разделить на множимое.

Что мы и сделали, когда выражали число 2 из равенства 3 × 2 = 6 . Тогда для получения числа 2 мы разделили произведение 6 на множимое 3.

А сейчас для нахождения неизвестного множителя x мы разделили произведение 6 на множимое 3.

Вычисление правой части равенства 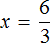позволяет узнать чему равно x

Множимое и множитель вместе называют сомножителями. Поскольку правила нахождения множимого и множителя совпадают, мы можем сформулировать общее правило нахождения неизвестного сомножителя:

Чтобы найти неизвестный сомножитель, нужно произведение разделить на известный сомножитель.

Например, решим уравнение 9 × x = 18 . Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 18 разделить на известный сомножитель 9

Отсюда .

Решим уравнение x × 3 = 27 . Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 27 разделить на известный сомножитель 3

Отсюда .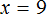

Вернемся к четвертому примеру из предыдущей темы, где в равенстве требовалось выразить число 15. В этом равенстве число 15 — это делимое, число 5 — делитель, число 3 — частное.

Чтобы выразить число 15 мы поступили следующим образом:

То есть умножили частное 3 на делитель 5.

Теперь представим, что в равенстве вместо числа 15 располагается переменная x

В этом случае переменная x берет на себя роль неизвестного делимого.

Для нахождения неизвестного делимого предусмотрено следующее правило:

Чтобы найти неизвестное делимое, нужно частное умножить на делитель.

Что мы и сделали, когда выражали число 15 из равенства . Чтобы выразить число 15, мы умножили частное 3 на делитель 5.

А сейчас, чтобы найти неизвестное делимое x , нужно частное 3 умножить на делитель 5

Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x .

Теперь представим, что в равенстве вместо числа 5 располагается переменная x .

В этом случае переменная x берет на себя роль неизвестного делителя.

Для нахождения неизвестного делителя предусмотрено следующее правило:

Чтобы найти неизвестный делитель, нужно делимое разделить на частное.

Что мы и сделали, когда выражали число 5 из равенства . Чтобы выразить число 5, мы разделили делимое 15 на частное 3.

А сейчас, чтобы найти неизвестный делитель x , нужно делимое 15 разделить на частное 3

Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x .

Итак, для нахождения неизвестных мы изучили следующие правила:

• Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое;
• Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое;
• Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность;
• Чтобы найти неизвестное множимое, нужно произведение разделить на множитель;
• Чтобы найти неизвестный множитель, нужно произведение разделить на множимое;
• Чтобы найти неизвестное делимое, нужно частное умножить на делитель;
• Чтобы найти неизвестный делитель, нужно делимое разделить на частное.

Компоненты

Компонентами мы будем называть числа и переменные, входящие в равенство

Так, компонентами сложения являются слагаемые и сумма

Компонентами вычитания являются уменьшаемое, вычитаемое и разность

Компонентами умножения являются множимое, множитель и произведение

Компонентами деления являются делимое, делитель и частное

В зависимости от того, с какими компонентами мы будем иметь дело, будут применяться соответствующие правила нахождения неизвестных. Эти правила мы изучили в предыдущей теме. При решении уравнений желательно знать эти правило наизусть.

Пример 1. Найти корень уравнения 45 + x = 60

45 — слагаемое, x — неизвестное слагаемое, 60 — сумма. Имеем дело с компонентами сложения. Вспоминаем, что для нахождения неизвестного слагаемого, нужно из суммы вычесть известное слагаемое:

Вычислим правую часть, получим значение x равное 15

Значит корень уравнения 45 + x = 60 равен 15.

Чаще всего неизвестное слагаемое необходимо привести к виду при котором его можно было бы выразить.

Пример 2. Решить уравнение

Здесь в отличие от предыдущего примера, неизвестное слагаемое нельзя выразить сразу, поскольку оно содержит коэффициент 2. Наша задача привести это уравнение к виду при котором можно было бы выразить x

В данном примере мы имеем дело с компонентами сложения — слагаемыми и суммой. 2x — это первое слагаемое, 4 — второе слагаемое, 8 — сумма.

При этом слагаемое 2x содержит переменную x . После нахождения значения переменной x слагаемое 2x примет другой вид. Поэтому слагаемое 2x можно полностью принять за неизвестное слагаемое:

Теперь применяем правило нахождения неизвестного слагаемого. Вычитаем из суммы известное слагаемое:

Вычислим правую часть получившегося уравнения:

Мы получили новое уравнение 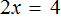. Теперь мы имеем дело с компонентами умножения: множимым, множителем и произведением. 2 — множимое, x — множитель, 4 — произведение

При этом переменная x является не просто множителем, а неизвестным множителем

Чтобы найти этот неизвестный множитель, нужно произведение разделить на множимое:

Вычислим правую часть, получим значение переменной x

Для проверки найденный корень отправим в исходное уравнение и подставим вместо x

Получили верное числовое равенство. Значит уравнение решено правильно.

Пример 3. Решить уравнение 3x + 9x + 16x = 56

Cразу выразить неизвестное x нельзя. Сначала нужно привести данное уравнение к виду при котором его можно было бы выразить.

Приведем подобные слагаемые в левой части данного уравнения:

Имеем дело с компонентами умножения. 28 — множимое, x — множитель, 56 — произведение. При этом x является неизвестным множителем. Чтобы найти неизвестный множитель, нужно произведение разделить на множимое:

Отсюда x равен 2

Равносильные уравнения

В предыдущем примере при решении уравнения 3x + 9x + 16x = 56 , мы привели подобные слагаемые в левой части уравнения. В результате получили новое уравнение 28x = 56 . Старое уравнение 3x + 9x + 16x = 56 и получившееся новое уравнение 28x = 56 называют равносильными уравнениями, поскольку их корни совпадают.

Уравнения называют равносильными, если их корни совпадают.

Проверим это. Для уравнения 3x + 9x + 16x = 56 мы нашли корень равный 2 . Подставим этот корень сначала в уравнение 3x + 9x + 16x = 56 , а затем в уравнение 28x = 56 , которое получилось в результате приведения подобных слагаемых в левой части предыдущего уравнения. Мы должны получить верные числовые равенства

Согласно порядку действий, в первую очередь выполняется умножение:

Подставим корень 2 во второе уравнение 28x = 56

Видим, что у обоих уравнений корни совпадают. Значит уравнения 3x + 9x + 16x = 56 и 28x = 56 действительно являются равносильными.

Для решения уравнения 3x + 9x + 16x = 56 мы воспользовались одним из тождественных преобразований — приведением подобных слагаемых. Правильное тождественное преобразование уравнения позволило нам получить равносильное уравнение 28x = 56 , которое проще решать.

Из тождественных преобразований на данный момент мы умеем только сокращать дроби, приводить подобные слагаемые, выносить общий множитель за скобки, а также раскрывать скобки. Существуют и другие преобразования, которые следует знать. Но для общего представления о тождественных преобразованиях уравнений, изученных нами тем вполне хватает.

Рассмотрим некоторые преобразования, которые позволяют получить равносильное уравнение

Если к обеим частям уравнения прибавить одно и то же число, то получится уравнение равносильное данному.

Если из обеих частей уравнения вычесть одно и то же число, то получится уравнение равносильное данному.

Другими словами, корень уравнения не изменится, если к обеим частям данного уравнения прибавить (или вычесть из обеих частей) одно и то же число.

Пример 1. Решить уравнение

Вычтем из обеих частей уравнения число 10

Приведем подобные слагаемые в обеих частях:

Получили уравнение 5x = 10 . Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x , нужно произведение 10 разделить на известный сомножитель 5.

Отсюда .

Вернемся к исходному уравнению и подставим вместо x найденное значение 2

Получили верное числовое равенство. Значит уравнение решено правильно.

Решая уравнение мы вычли из обеих частей уравнения число 10 . В результате получили равносильное уравнение . Корень этого уравнения, как и уравнения так же равен 2

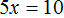
Пример 2. Решить уравнение 4(x + 3) = 16

Раскроем скобки в левой части равенства:

Вычтем из обеих частей уравнения число 12

Приведем подобные слагаемые в обеих частях уравнения:

В левой части останется 4x , а в правой части число 4

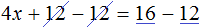
Получили уравнение 4x = 4 . Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x , нужно произведение 4 разделить на известный сомножитель 4

Отсюда

Вернемся к исходному уравнению 4(x + 3) = 16 и подставим вместо x найденное значение 1

Получили верное числовое равенство. Значит уравнение решено правильно.

Решая уравнение 4(x + 3) = 16 мы вычли из обеих частей уравнения число 12 . В результате получили равносильное уравнение 4x = 4 . Корень этого уравнения, как и уравнения 4(x + 3) = 16 так же равен 1

Пример 3. Решить уравнение

Раскроем скобки в левой части равенства:

Прибавим к обеим частям уравнения число 8

Приведем подобные слагаемые в обеих частях уравнения:

В левой части останется 2x , а в правой части число 9

В получившемся уравнении 2x = 9 выразим неизвестное слагаемое x

Отсюда

Вернемся к исходному уравнению и подставим вместо x найденное значение 4,5

Получили верное числовое равенство. Значит уравнение решено правильно.

Решая уравнение мы прибавили к обеим частям уравнения число 8. В результате получили равносильное уравнение . Корень этого уравнения, как и уравнения так же равен 4,5

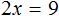
Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом

Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.

То есть корень уравнения не изменится, если мы перенесем слагаемое из одной части уравнения в другую, изменив его знак. Это свойство является одним из важных и одним из часто используемых при решении уравнений.

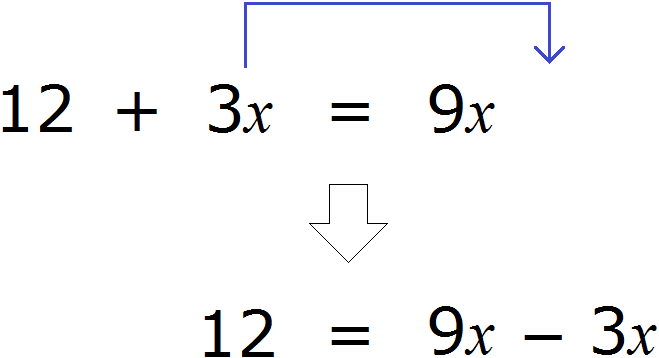
Рассмотрим следующее уравнение:

Корень данного уравнения равен 2. Подставим вместо x этот корень и проверим получается ли верное числовое равенство

Получается верное равенство. Значит число 2 действительно является корнем уравнения .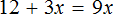

Теперь попробуем поэкспериментировать со слагаемыми этого уравнения, перенося их из одной части в другую, изменяя знаки.

Например, слагаемое 3x располагается в левой части равенства. Перенесём его в правую часть, изменив знак на противоположный:

Получилось уравнение 12 = 9x − 3x . Приведем подобные слагаемые в правой части данного уравнения:

Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:

Отсюда x = 2 . Как видим, корень уравнения не изменился. Значит уравнения 12 + 3x = 9x и 12 = 9x − 3x являются равносильными.

На самом деле данное преобразование является упрощенным методом предыдущего преобразования, где к обеим частям уравнения прибавлялось (или вычиталось) одно и то же число.

Мы сказали, что в уравнении 12 + 3x = 9x слагаемое 3x было перенесено в правую часть, изменив знак. В реальности же происходило следующее: из обеих частей уравнения вычли слагаемое 3x

Затем в левой части были приведены подобные слагаемые и получено уравнение 12 = 9x − 3x. Затем опять были приведены подобные слагаемые, но уже в правой части, и получено уравнение 12 = 6x.

Но так называемый «перенос» более удобен для подобных уравнений, поэтому он и получил такое широкое распространение. Решая уравнения, мы часто будем пользоваться именно этим преобразованием.

Равносильными также являются уравнения 12 + 3x = 9x и 3x − 9x = −12 . В этот раз в уравнении 12 + 3x = 9x слагаемое 12 было перенесено в правую часть, а слагаемое 9x в левую. Не следует забывать, что знаки этих слагаемых были изменены во время переноса

Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом:

Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному.

Другими словами, корни уравнения не изменятся, если обе его части умножить или разделить на одно и то же число. Это действие часто применяется тогда, когда нужно решить уравнение содержащее дробные выражения.

Сначала рассмотрим примеры, в которых обе части уравнения будут умножаться на одно и то же число.

Пример 1. Решить уравнение

При решении уравнений, содержащих дробные выражения, сначала принято упростить это уравнение.

В данном случае мы имеем дело именно с таким уравнением. В целях упрощения данного уравнения обе его части можно умножить на 8:

Мы помним, что для умножения дроби на число, нужно числитель данной дроби умножить на это число. У нас имеются две дроби и каждая из них умножается на число 8. Наша задача умножить числители дробей на это число 8

Теперь происходит самое интересное. В числителях и знаменателях обеих дробей содержится множитель 8, который можно сократить на 8. Это позволит нам избавиться от дробного выражения:

В результате останется простейшее уравнение

Ну и нетрудно догадаться, что корень этого уравнения равен 4

Вернемся к исходному уравнению и подставим вместо x найденное значение 4

Получается верное числовое равенство. Значит уравнение решено правильно.

При решении данного уравнения мы умножили обе его части на 8. В результате получили уравнение 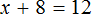. Корень этого уравнения, как и уравнения равен 4. Значит эти уравнения равносильны.

Множитель на который умножаются обе части уравнения принято записывать перед частью уравнения, а не после неё. Так, решая уравнение , мы умножили обе части на множитель 8 и получили следующую запись:

От этого корень уравнения не изменился, но если бы мы сделали это находясь в школе, то нам сделали бы замечание, поскольку в алгебре множитель принято записывать перед тем выражением, с которым он перемножается. Поэтому умножение обеих частей уравнения на множитель 8 желательно переписать следующим образом:

Пример 2. Решить уравнение

Умнóжим обе части уравнения на 15

В левой части множители 15 можно сократить на 15, а в правой части множители 15 и 5 можно сократить на 5

Перепишем то, что у нас осталось:

Раскроем скобки в правой части уравнения:

Перенесем слагаемое x из левой части уравнения в правую часть, изменив знак. А слагаемое 15 из правой части уравнения перенесем в левую часть, опять же изменив знак:

Приведем подобные слагаемые в обеих частях, получим

Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:

Отсюда

Вернемся к исходному уравнению 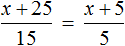и подставим вместо x найденное значение 5

Получается верное числовое равенство. Значит уравнение решено правильно. При решении данного уравнения мы умножили обе го части на 15 . Далее выполняя тождественные преобразования, мы получили уравнение 10 = 2x . Корень этого уравнения, как и уравнения 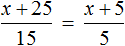равен 5 . Значит эти уравнения равносильны.

Пример 3. Решить уравнение

Умнóжим обе части уравнения на 3

В левой части можно сократить две тройки, а правая часть будет равна 18

Останется простейшее уравнение 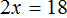. Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:

Отсюда

Вернемся к исходному уравнению 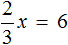и подставим вместо x найденное значение 9

Получается верное числовое равенство. Значит уравнение решено правильно.

Пример 4. Решить уравнение

Умнóжим обе части уравнения на 6

В левой части уравнения раскроем скобки. В правой части множитель 6 можно поднять в числитель:

Сократим в обеих частях уравнениях то, что можно сократить:

Перепишем то, что у нас осталось:

Раскроем скобки в обеих частях уравнения:

Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное x , сгруппируем в левой части уравнения, а слагаемые свободные от неизвестных — в правой:

Приведем подобные слагаемые в обеих частях:

Теперь найдем значение переменной x . Для этого разделим произведение 28 на известный сомножитель 7

Вернемся к исходному уравнению 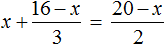и подставим вместо x найденное значение 4

Получилось верное числовое равенство. Значит уравнение решено правильно.

Пример 5. Решить уравнение

Раскроем скобки в обеих частях уравнения там, где это можно:

Умнóжим обе части уравнения на 15

Раскроем скобки в обеих частях уравнения:

Сократим в обеих частях уравнения, то что можно сократить:

Перепишем то, что у нас осталось:

Раскроем скобки там, где это можно:

Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Не забываем, что во время переноса, слагаемые меняют свои знаки на противоположные:

Приведем подобные слагаемые в обеих частях уравнения:

Найдём значение x

В получившемся ответе можно выделить целую часть:

Вернемся к исходному уравнению и подставим вместо x найденное значение

Получается довольно громоздкое выражение. Воспользуемся переменными. Левую часть равенства занесем в переменную A , а правую часть равенства в переменную B

Наша задача состоит в том, чтобы убедиться равна ли левая часть правой. Другими словами, доказать равенство A = B

Найдем значение выражения, находящегося в переменной А.

Значение переменной А равно . Теперь найдем значение переменной B . То есть значение правой части нашего равенства. Если и оно равно , то уравнение будет решено верно

Видим, что значение переменной B , как и значение переменной A равно . Это значит, что левая часть равна правой части. Отсюда делаем вывод, что уравнение решено правильно.

Теперь попробуем не умножать обе части уравнения на одно и то же число, а делить.

Рассмотрим уравнение 30x + 14x + 14 = 70x − 40x + 42 . Решим его обычным методом: слагаемые, содержащие неизвестные, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Далее выполняя известные тождественные преобразования, найдем значение x

Подставим найденное значение 2 вместо x в исходное уравнение:

Теперь попробуем разделить все слагаемые уравнения 30x + 14x + 14 = 70x − 40x + 42 на какое-нибудь число. Замечаем, что все слагаемые этого уравнения имеют общий множитель 2. На него и разделим каждое слагаемое:

Выполним сокращение в каждом слагаемом:

Перепишем то, что у нас осталось:

Решим это уравнение, пользуясь известными тождественными преобразованиями:

Получили корень 2 . Значит уравнения 15x + 7x + 7 = 35x − 20x + 21 и 30x + 14x + 14 = 70x − 40x + 42 равносильны.

Деление обеих частей уравнения на одно и то же число позволяет освобождать неизвестное от коэффициента. В предыдущем примере когда мы получили уравнение 7x = 14 , нам потребовалось разделить произведение 14 на известный сомножитель 7. Но если бы мы в левой части освободили неизвестное от коэффициента 7, корень нашелся бы сразу. Для этого достаточно было разделить обе части на 7

Этим методом мы тоже будем пользоваться часто.

Умножение на минус единицу

Если обе части уравнения умножить на минус единицу, то получится уравнение равносильное данному.

Это правило следует из того, что от умножения (или деления) обеих частей уравнения на одно и то же число, корень данного уравнения не меняется. А значит корень не поменяется если обе его части умножить на −1 .

Данное правило позволяет поменять знаки всех компонентов, входящих в уравнение. Для чего это нужно? Опять же, чтобы получить равносильное уравнение, которое проще решать.

Рассмотрим уравнение . Чему равен корень этого уравнения?

Прибавим к обеим частям уравнения число 5

Приведем подобные слагаемые:

А теперь вспомним про коэффициент буквенного выражения. Что же представляет собой левая часть уравнения 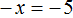. Это есть произведение минус единицы и переменной x

То есть минус, стоящий перед переменной x, относится не к самой переменной x , а к единице, которую мы не видим, поскольку коэффициент 1 принято не записывать. Это означает, что уравнение 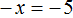на самом деле выглядит следующим образом:

Имеем дело с компонентами умножения. Чтобы найти х , нужно произведение −5 разделить на известный сомножитель −1 .

или разделить обе части уравнения на −1 , что еще проще

Итак, корень уравнения равен 5 . Для проверки подставим его в исходное уравнение. Не забываем, что в исходном уравнении минус стоящий перед переменной x относится к невидимой единице

Получилось верное числовое равенство. Значит уравнение решено верно.

Теперь попробуем умножить обе части уравнения на минус единицу:

После раскрытия скобок в левой части образуется выражение 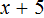, а правая часть будет равна 10

Корень этого уравнения, как и уравнения равен 5

Значит уравнения и равносильны.

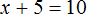
Пример 2. Решить уравнение

В данном уравнении все компоненты являются отрицательными. С положительными компонентами работать удобнее, чем с отрицательными, поэтому поменяем знаки всех компонентов, входящих в уравнение . Для этого умнóжим обе части данного уравнения на −1 .

Понятно, что от умножения на −1 любое число поменяет свой знак на противоположный. Поэтому саму процедуру умножения на −1 и раскрытие скобок подробно не расписывают, а сразу записывают компоненты уравнения с противоположными знаками.

Так, умножение уравнения на −1 можно записать подробно следующим образом:

либо можно просто поменять знаки всех компонентов:

Получится то же самое, но разница будет в том, что мы сэкономим себе время.

Итак, умножив обе части уравнения на −1 , мы получили уравнение . Решим данное уравнение. Из обеих частей вычтем число 4 и разделим обе части на 3

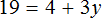
Когда корень найден, переменную обычно записывают в левой части, а её значение в правой, что мы и сделали.

Пример 3. Решить уравнение

Умнóжим обе части уравнения на −1 . Тогда все компоненты поменяют свои знаки на противоположные:

Из обеих частей получившегося уравнения вычтем 2x и приведем подобные слагаемые:

Прибавим к обеим частям уравнения единицу и приведем подобные слагаемые:

Приравнивание к нулю

Недавно мы узнали, что если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.

А что будет если перенести из одной части в другую не одно слагаемое, а все слагаемые? Верно, в той части откуда забрали все слагаемые останется ноль. Иными словами, не останется ничего.

В качестве примера рассмотрим уравнение 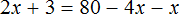. Решим данное уравнение, как обычно — слагаемые, содержащие неизвестные сгруппируем в одной части, а числовые слагаемые, свободные от неизвестных оставим в другой. Далее выполняя известные тождественные преобразования, найдем значение переменной x

Теперь попробуем решить это же уравнение, приравняв все его компоненты к нулю. Для этого перенесем все слагаемые из правой части в левую, изменив знаки:

Приведем подобные слагаемые в левой части:

Прибавим к обеим частям 77 , и разделим обе части на 7

Альтернатива правилам нахождения неизвестных

Очевидно, что зная о тождественных преобразованиях уравнений, можно не заучивать наизусть правила нахождения неизвестных.

К примеру, для нахождения неизвестного в уравнении мы произведение 10 делили на известный сомножитель 2

Но если в уравнении обе части разделить на 2 корень найдется сразу. В левой части уравнения в числителе множитель 2 и в знаменателе множитель 2 сократятся на 2. А правая часть будет равна 5

Уравнения вида мы решали выражая неизвестное слагаемое:

Но можно воспользоваться тождественными преобразованиями, которые мы сегодня изучили. В уравнении слагаемое 4 можно перенести в правую часть, изменив знак:

Далее разделить обе части на 2

В левой части уравнения сократятся две двойки. Правая часть будет равна 2. Отсюда .

Либо можно было из обеих частей уравнения вычесть 4. Тогда получилось бы следующее:

В случае с уравнениями вида удобнее делить произведение на известный сомножитель. Сравним оба решения:

Первое решение намного короче и аккуратнее. Второе решение можно значительно укоротить, если выполнить деление в уме.

Тем не менее, необходимо знать оба метода, и только затем использовать тот, который больше нравится.

Когда корней несколько

Уравнение может иметь несколько корней. Например уравнение x(x + 9) = 0 имеет два корня: 0 и −9 .

В уравнении x(x + 9) = 0 нужно было найти такое значение x при котором левая часть была бы равна нулю. В левой части этого уравнения содержатся выражения x и (x + 9) , которые являются сомножителями. Из законов умножения мы знаем, что произведение равно нулю, если хотя бы один из сомножителей равен нулю (или первый сомножитель или второй).

То есть в уравнении x(x + 9) = 0 равенство будет достигаться, если x будет равен нулю или (x + 9) будет равно нулю.

Приравняв к нулю оба этих выражения, мы сможем найти корни уравнения x(x + 9) = 0 . Первый корень, как видно из примера, нашелся сразу. Для нахождения второго корня нужно решить элементарное уравнение x + 9 = 0 . Несложно догадаться, что корень этого уравнения равен −9 . Проверка показывает, что корень верный:

Пример 2. Решить уравнение

Данное уравнение имеет два корня: 1 и 2. Левая часть уравнения является произведение выражений (x − 1) и (x − 2) . А произведение равно нулю, если хотя бы один из сомножителей равен нулю (или сомножитель (x − 1) или сомножитель (x − 2) ).

Найдем такое x при котором выражения (x − 1) или (x − 2) обращаются в нули:

Подставляем по-очереди найденные значения в исходное уравнение 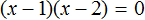и убеждаемся, что при этих значениях левая часть равняется нулю:

Когда корней бесконечно много

Уравнение может иметь бесконечно много корней. То есть подставив в такое уравнение любое число, мы получим верное числовое равенство.

Пример 1. Решить уравнение

Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения и привести подобные слагаемые, то получится равенство 14 = 14 . Это равенство будет получаться при любом x

Пример 2. Решить уравнение

Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения, то получится равенство 10x + 12 = 10x + 12. Это равенство будет получаться при любом x

Когда корней нет

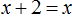
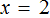
Случается и так, что уравнение вовсе не имеет решений, то есть не имеет корней. Например уравнение не имеет корней, поскольку при любом значении x , левая часть уравнения не будет равна правой части. Например, пусть . Тогда уравнение примет следующий вид

Пусть

Пример 2. Решить уравнение

Раскроем скобки в левой части равенства:

Приведем подобные слагаемые:

Видим, что левая часть не равна правой части. И так будет при любом значении y . Например, пусть y = 3 .

Буквенные уравнения

Уравнение может содержать не только числа с переменными, но и буквы.

Например, формула нахождения скорости является буквенным уравнением:

Данное уравнение описывает скорость движения тела при равноускоренном движении.

Полезным навыком является умение выразить любой компонент, входящий в буквенное уравнение. Например, чтобы из уравнения определить расстояние, нужно выразить переменную s .

Умнóжим обе части уравнения на t

В правой части переменные t сократим на t и перепишем то, что у нас осталось:

В получившемся уравнении левую и правую часть поменяем местами:

У нас получилась формула нахождения расстояния, которую мы изучали ранее.

Попробуем из уравнения определить время. Для этого нужно выразить переменную t .

Умнóжим обе части уравнения на t

В правой части переменные t сократим на t и перепишем то, что у нас осталось:

В получившемся уравнении v × t = s обе части разделим на v

В левой части переменные v сократим на v и перепишем то, что у нас осталось:

У нас получилась формула определения времени, которую мы изучали ранее.

Предположим, что скорость поезда равна 50 км/ч

А расстояние равно 100 км

Тогда буквенное уравнение примет следующий вид

Из этого уравнения можно найти время. Для этого нужно суметь выразить переменную t . Можно воспользоваться правилом нахождения неизвестного делителя, разделив делимое на частное и таким образом определить значение переменной t

либо можно воспользоваться тождественными преобразованиями. Сначала умножить обе части уравнения на t

Затем разделить обе части на 50

Пример 2. Дано буквенное уравнение 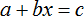. Выразите из данного уравнения x

Вычтем из обеих частей уравнения a

Разделим обе части уравнения на b

Теперь, если нам попадется уравнение вида a + bx = c , то у нас будет готовое решение. Достаточно будет подставить в него нужные значения. Те значения, которые будут подставляться вместо букв a, b, c принято называть параметрами. А уравнения вида a + bx = c называют уравнением с параметрами. В зависимости от параметров, корень будет меняться.

Решим уравнение 2 + 4x = 10 . Оно похоже на буквенное уравнение a + bx = c . Вместо того, чтобы выполнять тождественные преобразования, мы можем воспользоваться готовым решением. Сравним оба решения:

Видим, что второе решение намного проще и короче.

Для готового решения необходимо сделать небольшое замечание. Параметр b не должен быть равным нулю (b ≠ 0) , поскольку деление на ноль на допускается.

Пример 3. Дано буквенное уравнение 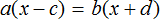. Выразите из данного уравнения x

Раскроем скобки в обеих частях уравнения

Воспользуемся переносом слагаемых. Параметры, содержащие переменную x , сгруппируем в левой части уравнения, а параметры свободные от этой переменной — в правой.

В левой части вынесем за скобки множитель x

Разделим обе части на выражение a − b

В левой части числитель и знаменатель можно сократить на a − b . Так окончательно выразится переменная x

Теперь, если нам попадется уравнение вида a(x − c) = b(x + d) , то у нас будет готовое решение. Достаточно будет подставить в него нужные значения.

Допустим нам дано уравнение 4(x − 3) = 2(x + 4) . Оно похоже на уравнение a(x − c) = b(x + d) . Решим его двумя способами: при помощи тождественных преобразований и при помощи готового решения:

Для удобства вытащим из уравнения 4(x − 3) = 2(x + 4) значения параметров a, b, c, d . Это позволит нам не ошибиться при подстановке:

Как и в прошлом примере знаменатель здесь не должен быть равным нулю (a − b ≠ 0) . Если нам встретится уравнение вида a(x − c) = b(x + d) в котором параметры a и b будут одинаковыми, мы сможем не решая его сказать, что у данного уравнения корней нет, поскольку разность одинаковых чисел равна нулю.

Например, уравнение 2(x − 3) = 2(x + 4) является уравнением вида a(x − c) = b(x + d) . В уравнении 2(x − 3) = 2(x + 4) параметры a и b одинаковые. Если мы начнём его решать, то придем к тому, что левая часть не будет равна правой части:

Пример 4. Дано буквенное уравнение 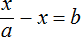. Выразите из данного уравнения x

Приведем левую часть уравнения к общему знаменателю:

Умнóжим обе части на a

В левой части x вынесем за скобки

Разделим обе части на выражение (1 − a)

Линейные уравнения с одним неизвестным

Рассмотренные в данном уроке уравнения называют линейными уравнениями первой степени с одним неизвестным.

Если уравнение дано в первой степени, не содержит деления на неизвестное, а также не содержит корней из неизвестного, то его можно назвать линейным. Мы еще не изучали степени и корни, поэтому чтобы не усложнять себе жизнь, слово «линейный» будем понимать как «простой».

Большинство уравнений, решенных в данном уроке, в конечном итоге сводились к простейшему уравнению, в котором нужно было произведение разделить на известный сомножитель. Таковым к примеру является уравнение 2 (x + 3) = 16 . Давайте решим его.

Раскроем скобки в левой части уравнения, получим 2 x + 6 = 16. Перенесем слагаемое 6 в правую часть, изменив знак. Тогда получим 2 x = 16 − 6. Вычислим правую часть, получим 2x = 10. Чтобы найти x , разделим произведение 10 на известный сомножитель 2. Отсюда x = 5.

Уравнение 2 (x + 3) = 16 является линейным. Оно свелось к уравнению 2x = 10 , для нахождения корня которого потребовалось разделить произведение на известный сомножитель. Такое простейшее уравнение называют линейным уравнением первой степени с одним неизвестным в каноническом виде. Слово «канонический» является синонимом слов «простейший» или «нормальный».

Линейное уравнение первой степени с одним неизвестным в каноническом виде называют уравнение вида ax = b.

Полученное нами уравнение 2x = 10 является линейным уравнением первой степени с одним неизвестным в каноническом виде. У этого уравнения первая степень, одно неизвестное, оно не содержит деления на неизвестное и не содержит корней из неизвестного, и представлено оно в каноническом виде, то есть в простейшем виде при котором легко можно определить значение x . Вместо параметров a и b в нашем уравнении содержатся числа 2 и 10. Но подобное уравнение может содержать и другие числа: положительные, отрицательные или равные нулю.

Если в линейном уравнении a = 0 и b = 0 , то уравнение имеет бесконечно много корней. Действительно, если a равно нулю и b равно нулю, то линейное уравнение ax = b примет вид 0x = 0 . При любом значении x левая часть будет равна правой части.

Если в линейном уравнении a = 0 и b ≠ 0 , то уравнение корней не имеет. Действительно, если a равно нулю и b равно какому-нибудь числу, не равному нулю, скажем числу 5, то уравнение ax = b примет вид 0x = 5 . Левая часть будет равна нулю, а правая часть пяти. А ноль не равен пяти.

Если в линейном уравнении a ≠ 0 , и b равно любому числу, то уравнение имеет один корень. Он определяется делением параметра b на параметр a

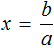
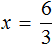
Действительно, если a равно какому-нибудь числу, не равному нулю, скажем числу 3 , и b равно какому-нибудь числу, скажем числу 6 , то уравнение примет вид .
Отсюда .

Существует и другая форма записи линейного уравнения первой степени с одним неизвестным. Выглядит она следующим образом: ax − b = 0 . Это то же самое уравнение, что и ax = b , но параметр b перенесен в левую часть с противоположным знаком. Такие уравнение мы тоже решали в данном уроке. Например, уравнение 7x − 77 = 0 . Уравнение вида ax − b = 0 называют линейным уравнением первой степени с одним неизвестным в общем виде.

В будущем после изучения рациональных выражений, мы рассмотрим такие понятия, как посторонние корни и потеря корней. А пока рассмотренного в данном уроке будет достаточным.