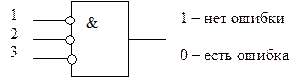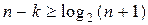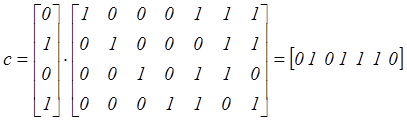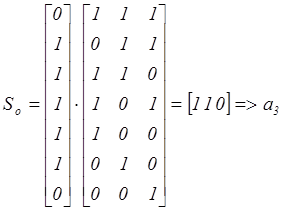Решение. Проверочная матрица позволяет выбрать алгоритм кодирования и декодирования, исходя из того, что единицы в каждой ее строке соответствуют тем символам кодовой
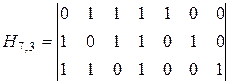
Проверочная матрица позволяет выбрать алгоритм кодирования и декодирования, исходя из того, что единицы в каждой ее строке соответствуют тем символам кодовой комбинации, сумма которых по модулю два должна быть равна 0. Так, из матрицы (3.29) можно получить следующие уравнения проверок:
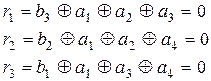
Естественно, что (3.27) и (3.30) полностью совпадают с той лишь разницей, что операции по (3.27) выполняются при кодировании для получения значений контрольных разрядов в каждой кодовой комбинации, а операции по (3.30) выполняются при декодировании для обнаружения и исправления ошибок.
Из анализа (3.30) видно, что a1 входит во все три уравнения, а2 — в первое и второе, а3 — в первое и третье, а4 — во второе и третье. Следовательно, искажение любого аi нарушит вполне определенные уравнения, т.е. сумма по модулю два в них будет рана не нулю, а единице. По тому, какие именно уравнения нарушены, можно определить, в каком разряде произошла ошибка, и восстановить его истинное значение.
Таким образом, результаты проверок дают кодовую комбинацию вида 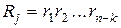
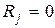
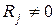
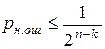
Для исправления ошибок каждому ненулевому синдрому может быть сопоставлен исправляющий вектор Ej , сумма по модулю два которого с принятой кодовой комбинацией образует переданную комбинацию. Пусть, например, передается кодовая комбинация из примера 3.8 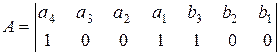
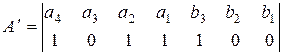
При выполнении проверок на приеме в соответствии с системой (3.30) получается
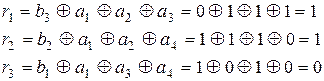
т.е. синдром R=110, нарушены первое и второе уравнения, в которые входит а2, следовательно, ошибка в разряде а2 и тогда исправляющий вектор Е=0010000, а исправленная кодовая комбинация
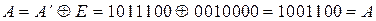
Пользуясь этим примером, обратим внимание на третью стоку образующей матрицы (3.26). В части этой строки, соответствующей единичной матрице, единица расположена на месте разряда, в котором произошла ошибка, а получившийся синдром R равен части этой же строки, входящей в дополняющую матрицу.
Обобщая, можно сказать, что при ошибке в разряде а4 синдром будет 011, при ошибке в разряде а3 — 101, при ошибке в разряде а1 — 111.
То же самое следует из проверочной матрицы этого кода (3.29), где первый столбец — синдром при ошибке в разряде а4 и т.д.
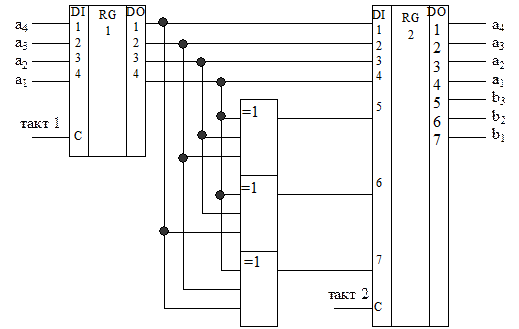
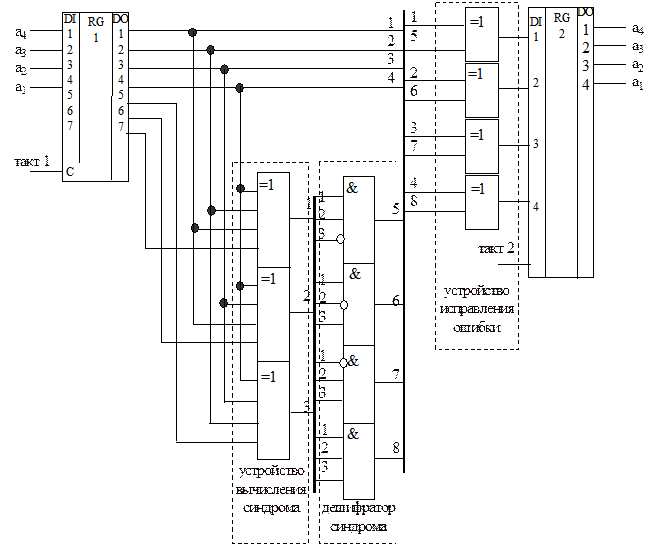
На основании любого из приведенных ранее описаний группового систематического кода (системы проверочных уравнений, образующей матрицы, проверочной матрицы) могут быть синтезированы функциональные схемы кодера и декодера такого кода.
Так, кодер (рис. 3.9) для кода из примера 3.8 должен содержать параллельный регистр, предназначенный для приема от источника и временного хранения четырех информационных разрядов, совокупность из трех трехвходовых сумматоров по модулю два, предназначенных для формирования значений контрольных разрядов, и параллельный семиразрядный регистр для промежуточного хранения сформированной кодовой комбинации, которая далее может быть последовательно передана в линию связи. Соединение входов сумматоров по модулю два с выходами первого регистра выполняются в соответствии с системой проверочных уравнений.
Сложность схемы декодера для такого кода будет зависеть от того, используется ли данный код в режиме обнаружения ошибки или в режиме исправления ошибки.
Для режима исправления ошибки в составе декодера (рис. 3.10) должны присутствовать следующие функциональные узлы:
— регистр для временного хранения принятой кодовой комбинации;
— устройство вычисления синдрома;
— устройство исправления ошибки;
— регистр для хранения исправленной информационной части комбинации.
Устройство вычисления синдрома представляет собой совокупность из трех сумматоров по модулю два, каждый из которых имеет по четыре входа, которые соединяются с выходами первого регистра в соответствии с системой проверочных уравнений, а выходы подключены к входам дешифратора синдрома. Дешифратор синдрома осуществляет преобразование синдрома в исправляющий вектор. Устройство исправления ошибок может быть реализовано в виде совокупности из четырех сумматоров по модулю два, каждый из которых имеет по два входа. Первые входы сумматоров соединяются с выходами информационных разрядов первого регистра, а вторые входы подключаются к соответствующим выходам дешифратора синдрома, а выходы соединены с соответствующими входами второго регистра.
Декодер, работающий в режиме обнаружения ошибок, проще, поскольку в нем отсутствует устройство исправления ошибок, а дешифратор синдрома может быть заменен одной схемой выявления ненулевого синдрома (рис. 3.11).
Рассмотренный алгоритм декодирования блоковых групповых линейных систематических (n, k)- кодов, называемый иногда синдромным, относится к классу алгебраических методов декодирования, в основе которых лежит решение системы уравнений, задающих расположение и значение ошибки.
Для декодирования этих кодов могут использоваться и неалгебраические методы, использующие простые структурные понятия теории кодирования, которые позволяют найти комбинации ошибок более прямым путем. Одним из таких алгоритмов является декодирование по максимуму правдоподобия.
Этот метод основывается на том предположении, что если все кодовые комбинации передаются по двоичному симметричному каналу с равной вероятностью, то наилучшим решением при приеме является такое, при котором переданной считается кодовая комбинация, отличающаяся от принятой в наименьшем числе разрядов.
В связи с этим алгоритм максимального правдоподобия реализуется в виде следующей последовательности действий:
1) принятая кодовая комбинация Y суммируется по модулю два последовательно со всеми кодовыми комбинациями кода Xi , в результате каждого суммирования вычисляются векторы ошибок ei = Y+Xi ,
2) подсчитывается число di единиц в каждом из векторов ошибки ei.
3) та из Xi, для которой di минимально, считается переданной кодовой комбинацией.
Для некоторых систематических (n,k)-кодов неравенство (3.23)
превращается в строгое равенство
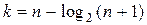
Для таких кодов можно записать 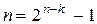
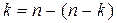
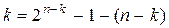
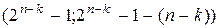
Образующая матрица кода Хэмминга (7,4) приведена ранее (3.26). Образующие матрицы кодов больших размерностей строятся аналогично. Уравнение (3.31) имеет целочисленные решения при k=0,1,4,11,26,57,120, . . , что дает соответствующие коды Хэмминга (3,1), (7,4), (15,11), (31,26), (63,57), (127,120),. . . . Коды Хэмминга относятся к немногим известным т.н. совершенным кодам.
С учетом данных ранее определений кодового пространства и кодового расстояния представим некоторый код в виде сфер с центрами во всех разрешенных кодовых комбинациях. Все сферы имеют одинаковый целочисленный радиус. Будем увеличивать его, оставляя целочисленным, до тех пор, пока сферы не соприкоснутся. Значение этого радиуса равно числу исправляемых кодом ошибок. Этот радиус называется радиусом сферической упаковки кода.
Теперь позволим этому радиусу увеличиваться до тех пор, пока каждая точка кодового пространства не окажется внутри хотя бы одной сферы. Такой радиус называется радиусом покрытия кода. Радиус упаковки и радиус покрытия кода могут совпадать.
Код, для которого сферы некоторого одинакового радиуса вокруг кодовых слов, не пересекаясь, покрывают все кодовое пространство, называются совершенными. Совершенный код удовлетворяет границе Хэмминга с равенством. Код Хэмминга, имеющий длину 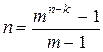
Код, у которого сферы радиуса t вокруг каждого кодового слова не пересекаются и все кодовые слова, не лежащие внутри какой-либо из этих сфер, находятся на расстоянии t+1 хотя бы от одного кодового слова, называется квазисовершенным. Квазисовершенные коды встречаются чаще, чем совершенные. Если для заданных n и k существует квазисовершенный и не существует совершенного кода, то для этих n и k не существует кода с большим, чем у квазисовершенного, кодовым расстоянием.
Систематические коды, в том числе и код Хэмминга, допускают различные преобразования, которые, порождая новые коды, тем не менее, не выводят их из класса линейных групповых кодов.
К числу наиболее часто используемых преобразований кодов относят укорочение и расширение кодов.
Укорочение кода состоит в уменьшении длины кодовых комбинаций путем удаления лишних информационных разрядов. Если код задан порождающей матрицей, то это приводит к уменьшению обоих размеров порождающей матрицы на одно и то же число. Так, например, как упоминалось ранее, коды Хэмминга с d=3 могут быть построены с вполне определенным сочетанием n и k. Как поступить в том случае, если требуется код Хэмминга с d=3, для передачи информации достаточно k=8, а на длину кодовой комбинации наложено ограничение n
Дата добавления: 2015-07-14 ; просмотров: 1528 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Кодирование с использованием линейного группового кода
Страницы работы
Содержание работы
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ
Кафедра “Обчислювальна техніка та програмування”
З лабораторних робіт
з курсу «Теорія інформації та кодування»
Ст. гр КIТЗI — 12
доц. Грінченко О.Г.
Ізюм 2005
Лабораторная работа №1
Линейный групповой код
Цель работы: Приобретение практических навыков кодирования с использованием линейного группового кода.
1. Построить линейный групповой код способный передавать сообщения в виде последовательности 16-ричных цифр первичного алфавита с исправлением одиночной ошибки. Показать процесс кодирования, декодирования и исправления однократной ошибки для произвольно выбранного информационного слова (например, 1010).
2. Составить программу, реализующую процесс кодирования, декодирования и исправления однократной ошибки с использованием линейного группового кода.
Порядок выполнения работы
1. Построение линейного группового кода
1. Выполним первичное кодирование, т. е. определим информационное слово для каждого символа первичного алфавита. Число информационных разрядов k для заданного объема кода можно определить из соотношения N = 16= 2 k = 2 4
Строим первичный код. При этом старшинство разрядов принимаем слева на право, в соответствии с их поступлением на вход кодера.
‘0’ => 0000 ‘4’ => 0010 ‘8’ => 0001 ‘C’ =>0011
‘1’ => 1000 ‘5‘=>1010 ‘9’ =>1001 ‘D’ =>1011
‘2’ => 0100 ‘6’ =>0110 ‘A’ => 0101 ‘E’ =>0111
‘3’ => 1100 ‘7’ =>1110 ‘B’ =>1101 ‘F’ =>1111
2. Определим основные параметры линейного кода: количество контрольных бит –m и длину кодовой комбинации – n по числу информационных бит (k = 4) и количеству исправляемых ошибок (S=1,do=3)
Длина кодовой комбинации равна n = k + m = 4 +3 = 7. При этом получили (7,4) – код.
3. Строим образующую (производящую, порождающую) матрицу
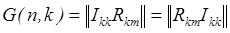
где: Ikk — информационная матрица, которая представляет единичную матрицу ранга k; Rkm, проверочная матрица, каждая строка которой содержит число единиц больше или равно двум (r1 £ d0-1).
Таким образом, в качестве производящей можно принять одну из матриц
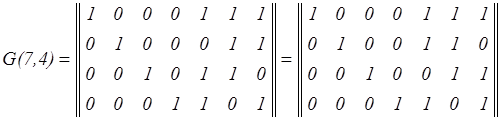
4. Процесс кодирования состоит во взаимно — однозначном соответствии k-разрядных информационных слов — I и n-разрядных кодовых слов — с
Например: информационному слову I=[ 0 1 0 1] соответствует следующее кодовое слово
Аналогично получим все остальные кодовые комбинации
5. Процесс декодирования состоит в определении соответствия принятого кодового слова, переданному информационному слову и осуществляется с помощью проверочной матрицы H(7, 4). Для построенного (7, 4)- кода проверочная матрица имеет вид
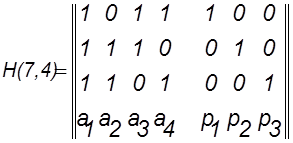
Строки проверочной матрицы определяют правила формирования проверок, позволяющие определить синдром ошибки.
6. Пусть F переданная кодовая комбинация, а F 1 принятая, т. е. в третьем бите произошла ошибка
F 1 = 0 1 1 1 1 1 0
Умножаем вектор столбец принятой кодовой комбинации на транспонированную проверочную, матрицу определим синдром ошибки
Синдром 110 показывает, что ошибка произошла в 3-м информационном разряде, который необходимо проинвертировать.
Отбросив контрольные биты, получим исходное информационное слово
I = [0101] => 1010 => ‘A’.
2. Программа реализации линейного группового кода
program L_cod_10; <Программа реализации линейного группового кода>
Определение проверочных равенств
Итак, для любого кода, имеющего целью исправлять наиболее вероятные вектора ошибок заданного канала связи (взаимно независимые ошибки или пачки ошибок), можно составить таблицу опознавателей одиночных ошибок в каждом из разрядов. Пользуясь этой таблицей, нетрудно определить, символы каких разрядов должны входить в каждую из проверок на четность.
Рассмотрим в качестве примера опознаватели для кодов предназначенных исправлять единичные ошибки (табл. 5.6).
Опознаватели одиночных ошибок
| Номер разряда | Опознаватель |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
| 16 | 10000 |
В принципе можно построить код, усекая эту таблицу на любом уровне. Однако, из таблицы видно, что оптимальными будут коды (7; 4), (15; 11), где первое число равно n, а второе k, и другие, которые среди кодов, имеющих одно и то же число проверочных символов, допускают наибольшее число информационных символов. http://peredacha-informacii.ru/ Усечем эту таблицу на седьмом разряде и найдем номера разрядов, символы которых должны войти в каждое из проверочных равенств.
Предположим, что в результате первой проверки на четность для младшего разряда опознавателя будет получена единица. Очевидно, это может быть следствием ошибки в одном из разрядов, опознаватели которых в младшем разряде имеют единицу. Следовательно, первое проверочное равенство должно включать символы 1, 3, 5 и 7-го разрядов:
Единица во втором разряде опознавателя может быть следствием ошибки в разрядах, опознаватели которых имеют единицу во втором разряде. Отсюда второе проверочное равенство должно иметь вид:
Аналогично находим и третье равенство:
Чтобы эти равенства при отсутствии ошибок удовлетворялись для любых значений информационных символов в кодовой комбинации, в нашем распоряжении имеется три проверочных разряда. Мы должны так выбрать номера этих разрядов, чтобы каждый из них входил только в одно из равенств. Это обеспечит однозначное определение значений символов в проверочных разрядах при кодировании. Указанному условию удовлетворяют разряды, опознаватели которых имеют по одной единице. В нашем случае это будут первый, второй и четвертый разряды.
Таким образом, для кода (7; 4), исправляющего одиночные ошибки, искомые правила построения кода, т.е. соотношения, реализуемые в процессе кодирования, принимают вид:
Поскольку построенный код имеет минимальное хэммингово расстояние dmin = 3, он в соответствии с d ≥ r + 1, может использоваться с целью обнаружения единичных и двойных ошибок. Обращаясь к табл. 5.6, легко убедиться, что сумма любых двух опознавателей единичных ошибок дает ненулевой опознаватель, что и является признаком наличия ошибки, но в этом случае нельзя исправить одиночные ошибки.
http://vunivere.ru/work25895
http://peredacha-informacii.ru/opredelenie-proverochnyh-ravenstv.html