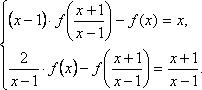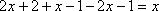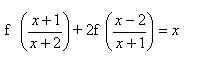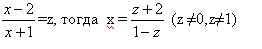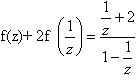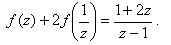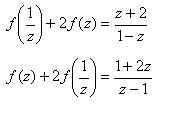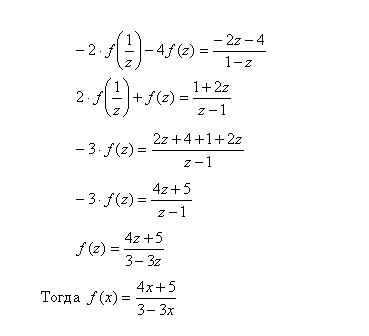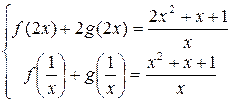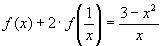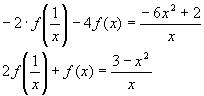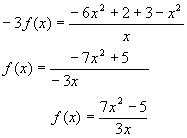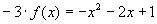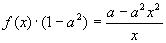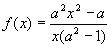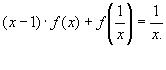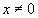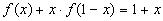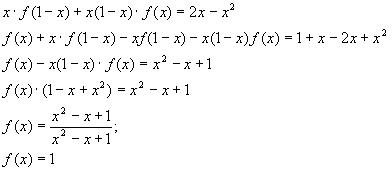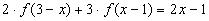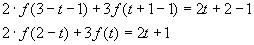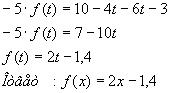Решением дифференциального уравнения
Главная > Решение
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Дифференциальные уравнения первого порядка
Дифференциальным уравнением называется уравнение, связывающее независимую переменную x, искомую функцию y(x) и производную искомой функции.
Символически дифференциальное уравнение можно написать так

Неизвестной здесь является функция y , входящая под знак производных (или дифференциалов).
Если искомая функция y(x) есть функция одной независимой переменной, то дифференциальное уравнение называется обыкновенным . В этой главе мы будем рассматривать только обыкновенные дифференциальные уравнения.
Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.
Например, уравнение 
а уравнение 
Решением дифференциального уравнения называется всякая функция y(x), которая будучи подставленной в уравнение, обращает его в тождество. Решение еще называется интегралом дифференциального уравнения.
Рассмотрим уравнение 
Функция 
Действительно,
и уравнение обращается в тождество: 
Решением рассматриваемого уравнения будут и функции
и вообще функции 


В самом деле
и уравнение обращается в тождество 
Заметим, что рассматриваемое уравнение имеет бесчисленное множество решений вида: 
Решение дифференциальных уравнений первого порядка
Дифференциальным уравнением первого порядка называется уравнение, связывающее независимую переменную x, искомую функцию y(x) и производную первого порядка искомой функции.
Дифференциальное уравнение первого порядка имеет вид 
Общее и частное решение
Общим решением дифференциального уравнения первого порядка называется решение 



Равенство вида 
Заметим, что в практике чаще всего бывает нужным не общее решение, а так называемое частное решение ,отвечающее определенным начальным условиям, вытекающим из условия данной конкретной задачи.
Частным решением называется любая функция 



Задача отыскания решения дифференциального уравнения y I = f(x,y) , удовлетворяющего заданным начальным условиям y(x o ) = y o , называется задачей Коши.
Теорема Коши
Если функция f(x,y) — правая часть дифференциального уравнения y I = f(x,y) — непрерывна в некоторой замкнутой области D плоскости xOy и имеет в этой области ограниченную частную производную f I y (x,y), то каждой внутренней точке области D соответствует, и притом единственное, решение, удовлетворяющее начальным условиям.
Рассмотрим уравнение 
Общим решением этого уравнения является семейство функций 
Действительно, при любом значении C эта функция удовлетворяет уравнению: 
Кроме того, всегда можно найти такое значение C, что соответствующее частное решение будет удовлетворять заданному начальному условию.
Найдем, например, частное решение, удовлетворяющее начальному условию y(1)=-2. Подставляя эти значения в уравнение 
получим 
Решая это уравнение относительно C получим C = — 3.
Следовательно, искомым частным решением будет функция: Y = X 2 — 3.
Это решение можно получить, используя нижеприведенный апплет для построения поля направлений и интегральных кривых для уравнения первого порядка.
С геометрической точки зрения общее решение уравнения первого порядка представляет собой семейство кривых на плоскости xOy , зависящее от одной произвольной постоянной C . Эти кривые называются интегральными кривыми данного дифференциального уравнения.
Частному решению соответствует одна интегральная кривая, проходящая через некоторую заданную точку. Так, в последнем примере общее решение геометрически изобразится семейством парабол, причем каждому значению параметра C будет соответствовать вполне определенная кривая. Частное решение изобразится параболой (рис. 1. 


Решить или проинтегрировать данное дифференциальное уравнение это значит:
а) найти его общее решение или общий интеграл, если не заданы начальные условия,
б) найти частное решение, удовлетворяющее заданным начальным условиям.
Геометрическая интерпретация дифференциального уравнения первого порядка
Пусть дано дифференциальное уравнение, разрешенное относительно производной: 
Это уравнение для каждой точки 

Таким образом, рассматриваемое дифференциальное уравнение дает совокупность направлений или, как говорят, определяет поле направлений или поле линейных элементов . Задача интегрирования такого уравнения, с геометрической точки зрения, заключается в нахождении кривых, направление касательных к которым совпадает с направлением поля линейных элементов в соответствующих точках .
Рассмотрим уравнение 
В каждой точке (x,y), отличной от точки (0,0), угловой коэффициент касательной к интегральной кривой равен отношению 
Теорема существования и единственности решения дифференциального уравнения.
Рассматривая уравнение первого порядка 

Возникает вопрос: всегда ли существует частное решение, удовлетворяющее заданному начальному условию и если существует, будет ли оно единственным.
Рассмотрим, например, уравнение 
Общим решением является функция 

Этот пример показывает, что не всегда существует решение, удовлетворяющее заданному начальному условию.
В некоторых случаях решение может оказаться не единственным.
Так, например, уравнение
имеет бесконечное множество решений, проходящих через точку (0,0) .
В самом деле, функция 



Теорема.
Пусть функция 




Геометрически это означает, что через каждую точку 
Возвращаясь к рассмотренным нами примерам, мы видим, что функции
и
не определены при 
1.1. Уравнения с разделяющимися переменными
Рассмотрим уравнение первого порядка, разрешенное относительно производной:
или 
Это уравнение можно переписать так:
или в симметричной форме

дающей соотношение между переменными x и y и их дифференциалами.
Если в этом уравнении функция P зависит только от x , а функция Q — только от y , то уравнение называется уравнением с разделенными переменными.
Таким образом, уравнением с разделенными переменными называется уравнение вида

Решение такого уравнения получается прямым интегрированием. Так как слева стоит сумма дифференциалов двух функций, которая равна нулю, то сумма их интегралов равняется постоянной

Уравнение 

Уравнение вида
называется уравнением с разделяющимися переменными .
Это уравнение может быть приведено к уравнению с разделенными переменными путем деления обеих его частей на выражение
или 
Общий интеграл полученного уравнения имеет вид:

Дано уравнение 

Разделим переменные 

В результате вычисления получим:

Это выражение можно записать в иной форме:
т.к. всякое число можно представить в виде логарифма другого.
Таким образом, общий интеграл данного уравнения будет иметь вид
.
1.2. Однородные уравнения первого порядка
Рассмотрим сначала понятие однородной функции двух переменных.
Функция двух переменных 
Функция 

С понятием однородной функции связано понятие однородного дифференциального уравнения.
называется однородным дифференциальным уравнением первого порядка ,
если функции 

Для однородного уравнения имеем:

Полагая в последних равенствах 

Подставив эти выражения в исходное уравнение, получим


Для разделения переменных введем новую переменную V = y/x или y = V x . Так как в этом случае dy = xd V + V dx , то последнее уравнение принимает вид:
M (1,V)dx + N(1,V)(xdV + Vdx) = 0 ,
[ M (1, V ) + vN (1, V )] dx + xN (1, V ) dV = 0 .
Последнее уравнение является уравнением с разделяющимися переменными x и V , из него определяется V , а затем искомая функция y = V x .
Если уравнение может приведено к виду: dy/dx = F(x,y) = F(v) , где V = y/x , то оно называется однородным дифференциальным уравнением первого порядка .
Для приведения его к уравнению с разделяющимися переменными используется подстановка
V = y/x , отсюда y = V x и dy/dx = xd V /dx + V .
В итоге получается уравнение с разделяющимися переменными: xd V /dx = F( V ) — V , которое и интегрируется.
Решить уравнение (y 2 — 3x 2 )dx + 2xydy = 0, при начальном условии: y(0) = 0 .
Здесь M(x,y) = (y 2 — 3x 2 ) и N(x,y) = 2xy — однородные функции измерения 2.
Применим подстановку y = vx, при этом dy = xdv +vdx.
Получим: x 2 (v 2 — 3)dx + 2x 2 v(xdv +vdx) = 0.
Сгруппируем слагаемые x 2 (v 2 — 3)dx + 2x 2 v(xdv +vdx) = 0 относительно dx и dv и разделим переменные:

После интегрирования получим: x 3 (v 2 — 1) = C или
общий интеграл: x(y 2 — x 2 ) = C
Используя начальные условия y(0) = 0 имеем 0(0 2 — 0 2 ) = C , отсюда C = 0.
Частное решение данного уравнения: x(y 2 — x 2 ) = 0
или x = y и x = — y
1.3. Линейные уравнения первого порядка

где 
— заданные непрерывные функции, называется линейным дифференциальным уравнением первого порядка.
Если функция 

то уравнение называется линейным однородным , в противном случае — линейным неоднородным .
Таким образом, 

Рассмотрим два метода интегрирования линейных уравнений.
I метод — метод Бернулли
Для решения уравнения применим подстановку y=UV , причем функцию U=U(x) будем считать новой неизвестной функцией, а функцию 

и
Используя произвольный выбор функции V , подчиним ее условию: 
Разделяя переменные и интегрируя в последнем равенстве, получаем:

Поэтому исходное уравнение после подстановки полученной функции V(x) имеет вид: 
Это уравнение также является уравнением с разделяющимися переменными.
Решая его, получаем: 

Возвращаясь к переменной y=UV имеем общее решение линейного неоднородного уравнения: 
Решить уравнение 
Здесь 
Имеем:


II метод — метод вариации произвольной постоянной — метод Лагранжа
В линейном однородном уравнении 

Будем теперь находить общее решение неоднородного линейного уравнения 

Дифференцируя это выражение
и подставляя в рассматриваемое неоднородное уравнение, получим:


Откуда находим функцию C(x) :


Полученное общее решение состоит из двух слагаемых, из которых второе 


Найти общее решение уравнения 
Интегрируем соответствующее однородное уравнение: 
Считаем C функцией x :
Подставляем в исходное уравнение: 
1.4. Уравнение Бернулли
Уравнением Бернулли называется уравнение вида dy/dx + P(x)y = Q(x)y n .
При n = 0 или n = 1 уравнение становится линейным, методы интегрирования которого рассматривались в предыдущем пункте.
Есть следующие два способа интегрирования этого уравнения.
1 . Уравнение приводится к линейному.
Разделив все члены такого уравнения на y n , получим:
y -n (dy/dx) + P(x)y -n+1 = Q(x) .
Сделаем замену: y -n+1 = z . Тогда dz / dx = (- n +1) y — n dy / dx .
После подстановки этих выражений в уравнение оно примет вид:
dz/dx + (1-n)P(x)z = (1-n)Q(x) .
Это линейное уравнение относительно функции z . После его интегрирования возвращаемся к переменной y, подставив вместо z выражение y 1-n . Получим общий интеграл уравнения Бернулли.
2. Уравнение решается по методу Бернулли с подстановкой y = UV , уже использованному для решения линейных неоднородных уравнений.
Найти общее решение уравнения 
Разделив обе части уравнения на y 2 , получим:

Введем новую переменную 

Подставляя в уравнение, получим:
Это линейное уравнение относительно функции z( x ) .
Применим метод вариации произвольной постоянной:
Интегрируя по частям, находим 
следовательно 

Заменяя теперь z на 
получим: 

Это и есть общее решение исходного уравнения.
1.5. Уравнения в полных дифференциалах
Уравнением в полных дифференциалах называется уравнение вида

левая часть которого есть полный дифференциал некоторой функции 

Переписав исходное уравнение в виде 

Как известно, полный дифференциал функции 


Необходимое и достаточное условие того, что левая часть уравнения является полным дифференциалом некоторой функции, выражается равенством

Функция 

Проинтегрировать дифференциальное уравнение

Для данного уравнения

Так как выполнено условие (#), то данное уравнение является уравнением в полных дифференциалах, следовательно,

Интегрируя первое из этих уравнений ( y при этом считается постоянным), находим

где 
Дифференцируя по y функцию U(x,y) = C и принимая во внимание значение 
получаем 
откуда 
Подставив выражение для
в равенство 
найдем 
В соответствии с формулой
получаем
или 
где 
Итак, общий интеграл данного уравнения:
Это уравнение является также однородным и его можно проинтегрировать другим способом.
Функциональные уравнения. Методы их решения
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Министерство образования и молодежной политики Чувашской Республики
БОУ ДПО (ПК) С «Чувашский республиканский институт образования»
Кафедра математики и информационных технологий
Курсовая работа на тему:
« Функциональные уравнения. Методы их решения»
Выполнил (а): учитель математики МБОУ «СОШ № 60»
Глава 1. Понятие функционального уравнения ………………………………. 5
Глава 2. Практическая часть. Методы решения функционального уравнения.9
Одно из важнейших математических умений, которым должны овладеть учащиеся школы, — умение решать уравнения. Корень уравнения находят в одно или более действий, многие текстовые задачи решаются алгебраическим способом, в уравнении могут участвовать целые, рациональные и другие числа, то есть уравнения одновременно сами по себе являются задачами и способами решения задач, умение, решать, которые необходимы всем учащимся школы. Но во время решения тренировочных заданий мне попалось уравнение, которое я решить не смогла. Как я узнала позже от учителя, это было функциональное уравнение.
Что же такое функциональные уравнения? И какие способы их решения существуют? Эти вопросы заинтересовали меня, и я решила провести исследование. функциональный уравнение коши
Функциональными уравнениями занимаются с очень давних пор, этому курсу так и не нашлось достойного места в математических программах. А жаль. Ведь решение отдельных функциональных уравнений требует достаточно глубокого понимания предмета и прививает любовь к самостоятельной творческой работе. Так как эта тема в школьном курсе не изучается в виду её сложности, при поступлении в престижные ВУЗы, на олимпиадах, в части С ЕГЭ такие задачи встречаются.
В настоящее время практически нет никаких пособий, обучающих решению функциональных уравнений.
Поэтому ощущается потребность в пособии, которое на простых и конкретных примерах способно показать читателю со скромной математической подготовкой весь арсенал современных методов решения функциональных уравнений.
Цель работы — выяснить, что является функциональным уравнением их системами, найти способы решения и составить сборник задач для использования математическими классами.
1. изучение и анализ литературы;
2. поиск способов решения функциональных уравнений и их систем;
3. решение функциональных уравнений
4. составление сборника
Объект исследования: функциональные уравнения
Предмет исследования: изучение свойств и способов решения функциональных уравнений.
Структура: введение, понятие функционального уравнения, сборник задач, заключение.
Глава 1. Понятие функционального уравнения
Функциональное уравнение – это уравнение, которое содержит одну или несколько неизвестных функций (с заданными областями определения и значений). Решить функциональное уравнение – это, значит, найти все функции, которые тождественно ему удовлетворяют. Функциональные уравнения возникают в самых различных областях математики, обычно в тех случаях, когда требуется описать все функции, обладающие заданными свойствами. Термин функциональное уравнение обычно используется для уравнений, несводимых простыми способами к алгебраическим уравнениям. Эта несводимость чаще всего обусловлена тем, что аргументами неизвестной функции в уравнении являются не сами независимые переменные, а некоторые данные функции от них. Часто встречаются на различных математических соревнованиях.
Некоторые функциональные уравнения знакомы нам еще из школьного курса это
которые задают такие свойства функций, как чётность, нечётность, периодичность.
Задача решения функциональных уравнений является одной из самых старых в математическом анализе. Они появились почти одновременно с зачатками теории функций. Первый настоящий расцвет этой дисциплины связан с проблемой параллелограмма сил. Ещё в 1769 году Даламбер свёл обоснование закона сложения сил к решению функционального уравнения

То же уравнение и с той же целью было рассмотрено Пуассоном в 1804 году при некотором предположении аналитичности, между тем как в 1821 году Коши (1789 – 1857) нашёл общие решения
этого уравнения, предполагая только непрерывность f(x).
Даже известная формула неевклидовой геометрии для угла параллельности
была получена Н. И. Лобачевским (1792 – 1856) из функционального уравнения

которое он решил методом, аналогичным методу Коши. Это уравнение можно привести к уравнению

Ряд геометрических задач, приводящих к функциональным уравнениям, рассматривал английский математик Ч. Баббедж (1792—1871). Он изучал, например, периодические кривые второго порядка, определяемые следующим свойством для любой пары точек кривой: если абсцисса второй точки равна ординате первой, то ордината второй точки равна абсциссе первой. Пусть такая кривая является графиком функции у = f(х) ; (х, f(х)) — произвольная ее точка. Тогда, согласно условию, точка с абсциссой f(х) имеет ординату х. Следовательно,

Функциональному уравнению (3) удовлетворяют, в частности, функции:

Одними из простейших функциональных уравнений являются уравнения Коши
Эти уравнения Коши подробно изучил в своём (Курсе Анализа), изданном в 1821 году. Непрерывные решения этих четырёх основных уравнений имеют соответственно вид



В классе разрывных функций могут быть и другие решения. Уравнение (4) ранее рассматривалось Лежандром и Гауссом при выводе основной теоремы проективной геометрии и при исследовании гауссовского закона распределения вероятностей.
Функциональное уравнение (4) было опять применено Г. Дарбу к проблеме параллелограмма сил и к основной теореме проективной геометрии; его главное достижение — значительное ослабление предположений. Мы знаем, что функциональное уравнение Коши (4) характеризует в классе непрерывных функций линейную однородную функцию f(x) = ax . Дарбу же показал, что всякое решение, непрерывное хотя бы в одной точке или же ограниченное сверху (или снизу) в произвольно малом интервале, также должно иметь вид f(x) = ax. Дальнейшие результаты по ослаблению предположений следовали быстро один за другим (интегрируемость, измеримость на множестве положительной меры и даже мажорируемость измеримой функцией). Возникает вопрос: существует ли хоть одна какая-нибудь аддитивная функция (т. е. удовлетворяющая (4)), отличная от линейной однородной. Найти такую функцию действительно нелегко! В ходе работы мы покажем, что при рациональных x значения любой аддитивной функции должны совпадать со значениями некоторой линейной однородной функции, т. е. f(x) = ax для x 
Многие функциональные уравнения не определяют конкретную функцию, а задают широкий класс функций, т. е. выражают свойство, характеризующее тот или иной класс функций. Например, функциональное уравнение f(x+1) = f(x) характеризует класс функций, имеющих период 1, а уравнение f(1+x) = f(1-x) — класс функций, симметричных относительно прямой x = 1 , и т. д.
Решение функциональных уравнений методом подстановки
Заменяя некоторые переменные функционального уравнения либо конкретными значениями, либо какими-либо другими выражениями пытаемся либо упростить это уравнение, либо привести его к такому виду, что дальнейшее решение станет очевидным. Особенность применяемого метода как раз и состоит в том, что в ряде случаев он позволяет отыскать решения в классе всевозможных функций.
1. Найдите все функции, определённые на множестве 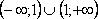
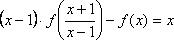
Решение:
Придадим x значение 

Отсюда 
Получим систему
Из уравнения (1) выразим 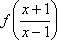
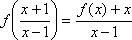
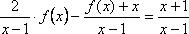
Отсюда 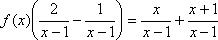


Проверим, действительно ли функция f(x) удовлетворяет уравнению 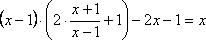
Ответ: 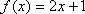
2. Найти функцию, удовлетворяющую уравнению
Решение:
2) Подставим в исходное уравнение, получим
3)Заменим z на 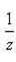
или после преобразований в правой части уравнения:
4)Итак, получили два уравнения:
5)Умножим обе части 1-го уравнения на (-2) и сложим со 2-ым уравнением, получим:
3.Пусть 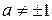

Решение:При замене
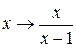

решением которой при a 2 ≠ 1 является функция
Ответ:
4.Найти решение системы функциональных уравнений относительно неизвестных функций f(x) и g(x):
Решение:
В первом уравнении сделаем подстановку 2x = 1/z.
и первое уравнение принимает вид:
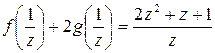
В результате получаем систему уравнений:
решение которой g(x) = 1/x, f(x) = x+1.
Ответ:g(x) = 1/x, f(x) = x+1.
5.Найдите все функции f: R à R, которые при всех х, у ? R удовлетворяют уравнению f(х+у)=х+уf(х)+(1-х)у. (1)
Решение:
Пусть f − функция удовлетворяющая уравнению (1). Поскольку (1) выполняется при всех значениях переменных х и у, то оно будет выполнятся и при конкретных значениях этих переменных. Подставив, например, у = 0 в исходное уравнение, мы получим f(х)=х. Это равенство должно выполнятся при любом действительном х.
Таким образом, (1) => f(х)≡х или, иными словами, никакая функция кроме f(х)≡х не может удовлетворять уравнению (1). Это, тем не менее, не доказывает, что функция f(х)≡х является решением функционального уравнения (1). Непосредственная проверка показывает, что найденная функция действительно удовлетворяет уравнению при всех х,у ? R.
6.Найдите все функции f: R à R, которые при всех х, у ? R удовлетворяют уравнению f(х+у)=х+уf(х)+(1-sin х)у. (2)
Решение:
Точно также, как и в предыдущей задаче, устанавливаем, что для функции f, которая удовлетворяет (2), должно выполнятся тождество f(х)≡х. Однако, подставив функцию f(х)=х в (2), мы тождества не получим. Поскольку никакие другие функции также не могут быть решениями (2), то данное уравнение решений не имеет.
7.Найдите все функции f: R à R, которые при всех х, у ? R удовлетворяют уравнению
f(х+у 2 +2у+1) = у 4 +4у 3 +2ху 2 +5у 2 +4ху+2у+х 2 +х+1. (3)
Решение:
Поскольку мы хотим получить значение f(х), попробуем избавится от слагаемого у 2 +2у+1 под знаком функции. Уравнение у 2 +2у+1=0 имеет одно решение у=-1. Подставляя у= -1 в (3) получаем f(х)= х 2 -х+1 .
Ответ: f(х)= х 2 -х+1.
8.Найдите все функции f: R à R, которые при всех х, у ? R удовлетворяют уравнению
f((х 2 +6х+6)у)=у 2 х 4 +12у 2 х 3 +48у 2 х 2 -4ух 2 +72у 2 х-24ух+36у 2 -24 (4)
Решение:
Как и в прошлой задаче, мы хотим получить под знаком функции свободную переменную (х или у). В данном случае, очевидно, проще получить у. Решив уравнение х 2 +6х+6)у=0 относительно х получаем х1= -1, х2= -5. Подстановка любого из этих значений в (4) дает нам f(у)=у 2 -4у.
9.Решите следующие функциональные уравнения.
в) f(x+y)+f(x-y)=2f(x)cos y
Решение:
а) Положим у=1/x. Тогда f(1/y) + 2f(y) =3/y и f(y)+2f(1/y)=3y. Отсюда f(y)= 2/y – y.
б) Положим y=x-1/x , затем z=y-1/y. Получим систему трёх линейных уравнений относительно f(x), f(y), f(z), з которой находим
в) Положив у=π/2, получаем f(х+π/2) +f(x-π/2)=0 для любого х, откуда f(x+π)= — f(x). Заменив у на у+π/2, получаем
заменив теперь х- π/2 на х, имеем:
и с учетом предыдущего:
Положив х=0, получаем отсюда и из исходного уравнения:
Таким образом, искомая функция должна иметь вид a cos y +b sin y, где a,b – константы.
10.
Решение: 1) Заменим 
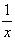
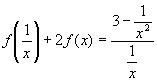

2)Умножим обе части уравнения из п.1 на (-2) и сложим с исходным уравнением:
11. 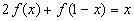
Решение: 1)Заменим в уравнении 
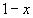
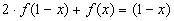
2) Умножим обе части исходного уравнения 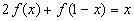
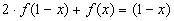
получим:
12.
Решение:
1) Заменим в уравнение 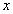
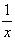
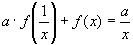
2)Умножим уравнение 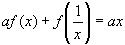

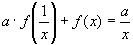
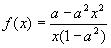
13.
Решение:
1)Заменим в уравнении 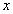
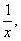
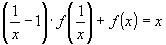
2)Выразим из исходного уравнения 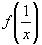
или 
3)Подставим 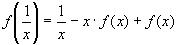
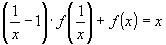

14.
Решение:
1.Заменим 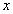
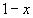
2.Умножим обе части уравнения 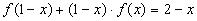

15.
Решение:1)Пусть 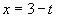
2)Пусть 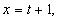
3)Умножим обе части уравнения из п.1 на 2, а обе части уравнения из п.2 на (-3) и почленно сложим получившиеся уравнения:
16.
Решение:
1) Заменим 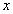
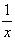
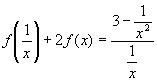

2)Умножим обе части уравнения из п.1 на (-2) и сложим с исходным уравнением:
http://infourok.ru/funkcionalnie-uravneniya-metodi-ih-resheniya-403500.html
http://megalektsii.ru/s5548t2.html