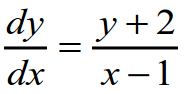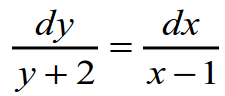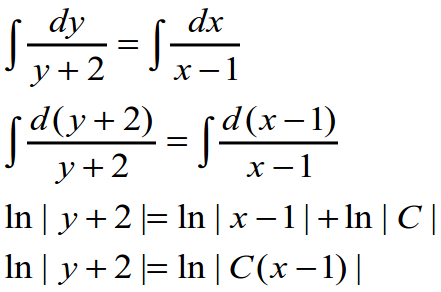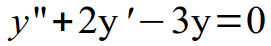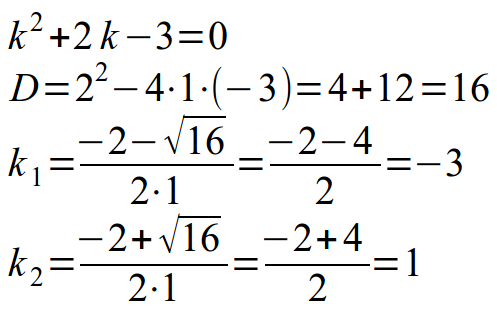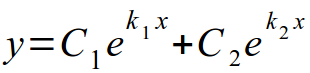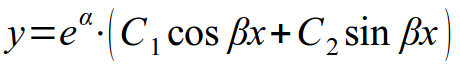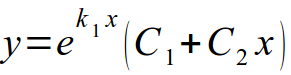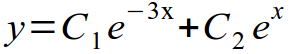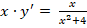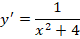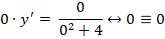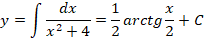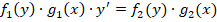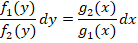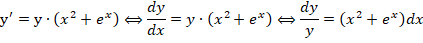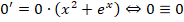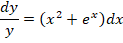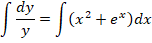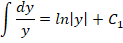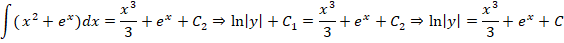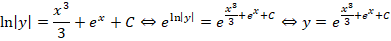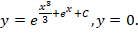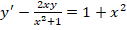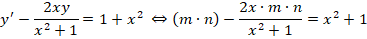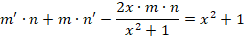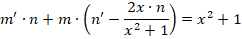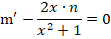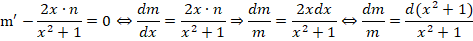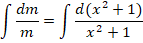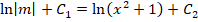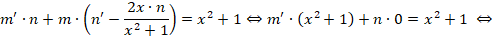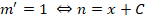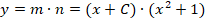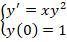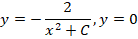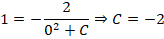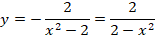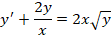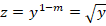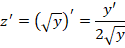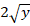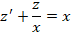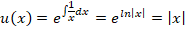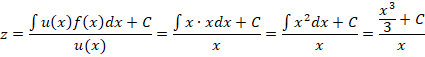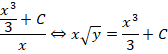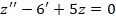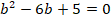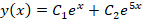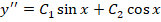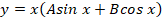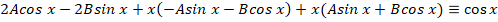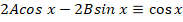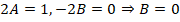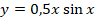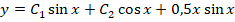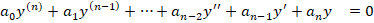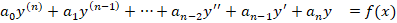Дифференциальные уравнения. Что это?
| Срок выполнения | от 1 дня |
| Цена | от 100 руб./задача |
| Предоплата | 50 % |
| Кто будет выполнять? | преподаватель или аспирант |
Вы уже имеете находить производные и интегралы? Тогда настало самое время, чтобы перейти к более сложной теме, а именно, решению дифференциальных уравнений (ДУ, в простонародье диффуров). Но не все так страшно, как кажется на первый взгляд.
Дифференциальное уравнение: что это такое?
Дифференциальное уравнение (ДУ) – это уравнение, которое вместе с самой функцией (и ее аргументами), содержит еще и ее производную или несколько производных.
Дифференциальное уравнение: что нужно знать еще?
Первое (и главное), что понадобится, это умение правильно определять тип дифференциального уравнения. Второе, но не менее важное, это умение хорошо интегрировать и дифференцировать.
Не секрет, что дифференциальные уравнения бывают разных типов. Но… для начала отметим, что ДУ бывают разных порядков. Порядок ДУ — это порядок высшей производной, входящей в дифференциальное уравнение. Классификацию ДУ согласно порядку уравнения можно посмотреть в следующей таблице:
| Порядок уравнения | Вид уравнения | Пример |
|---|---|---|
| I | 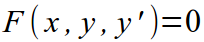 | 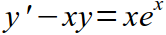 |
| II | 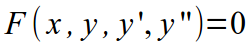 | 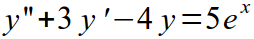 |
| … | … | … |
| n | 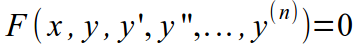 | 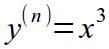 |
Наиболее часто приходится иметь дело с ДУ первого и второго порядка, реже третьего. В 99% случаев в задачах встречаются три типа ДУ первого порядка: уравнения с разделяющимися переменными, однородные уравнения и линейные неоднородные уравнения. Иногда еще встречаются более редкие типы ДУ: уравнения в полных дифференциалах, уравнения Бернулли и др. Среди ДУ второго порядка часто встречаются уравнения, приводящиеся к ДУ первого порядка, линейные однородные и неоднородные уравнения с постоянными коэффициентами.
Дифференциальное уравнение: решение – что это значит и как его найти?
При решении ДУ нам предлагается найти либо общее решение (общий интеграл), либо частное решение. Общее решение y = f(x, C) зависит от некоторой постоянной ( С — const), а частное решение не зависит: y = f(x, C0).
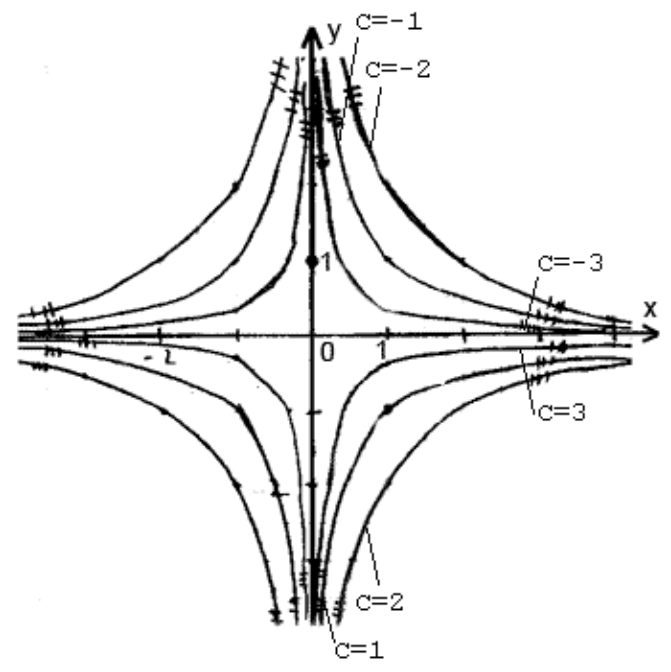
С геометрической точки зрения общее решение – это семейство кривых на координатной плоскости, а частное решение – это одна прямая этого семейства, проходящая через некоторую точку.
Давайте рассмотрим примеры решения некоторых ДУ. Начнем с ДУ первого порядка с разделяющимися переменными:
Здесь все очень просто как на уроке физкультуры, когда ученики класса делятся на две команды, в одну из которых входят только мальчики, а в другую – только девочки. Применительно к уравнению делаем следующее: в левую часть от знака равенства переносим все то, что содержит переменную y, а в правую часть – переменную x.
Получаем:
Далее интегрируем обе части:
Итоговое общее решение выглядит следующим образом: y = C(x-1) — 2. Все оказалось очень просто, не правда ли?
Не сложнее и решение однородных ДУ второго порядка с постоянными коэффициентами. Здесь всего-то и нужно знать из курса школьной алгебры, как решаются квадратные уравнения, а из курса по ДУ, как правильно записать общее решение.
Для наглядности рассмотрим пример:
Составляем характеристическое уравнение, заменяя переменную y на переменную k, а количество штрихов соответствующей степенью (два штриха – степень 2, один штрих – степень 1, нет штрихов – степень 0). Получаем квадратное уравнение, решить которое можно с помощью дискриминанта или теоремы Виета:
После того, как корни характеристического уравнения найдены, вспоминаем правила записи общего решения однородного ДУ:
- Корни характеристического уравнения являются действительными и различными. Общее решение записывается в виде:
- Корни характеристического уравнения являются комплексными. Общее решение записывается в виде:
- Корни характеристического уравнения являются действительными и равными. Общее решение записывается в виде:
Вспоминаем, что наше уравнение имеет два различных действительных корня. Следовательно, общее решение запишем в виде:
Решение линейных неоднородных ДУ с постоянными коэффициентами выполняется в два этапа:
- нахождение общего решения линейного однородного ДУ;
- нахождение и частного решения линейного неоднородного ДУ.
Выполнение первого этапа рассмотрено на примере чуть раньше. То, в каком виде мы будем искать частное решение неоднородного ДУ, зависит от того, что стоит в уравнении справа от знака равенства. Все возможные случаи подробно рассматривают в учебной литературе.
Итак, тема «Решение задач по дифференциальным уравнениям» изучается в ВУЗах, но, как было показано выше, решить некоторые ДУ может и школьник.
Дифференциальные уравнения и методы их решения рассматриваются практически в каждом учебнике по высшей математике и математическому анализу. Особенно хорошо данная тема рассмотрена в учебнике автора Пискунов Н.С., а называется он «Дифференциальное и интегральное исчисления: Учеб. Для втузов. В 2-х т. Т. II». С помощью данного учебника можно самостоятельно изучить методы решения тех типов ДУ, которые не были рассмотрены в данной статье.
Решение дифференциальных уравнений на заказ
У нас вы можете выгодно заказать решение задач с дифференциальными уравнениями. Нами накоплен большой опыт решения заданий по данной дисциплине, которым мы готовы поделиться с вами. Работа будет оформлена очень подробно. При заказе большого количества задач действует скидка. Купить решение можно, сделав заказ у нас на сайте.
Основные понятия и определения дифференциальных уравнений
Дифференциальным уравнением называется уравнение, связывающее независимую переменную , искомую функцию и её производные , т. е. уравнение вида
Если искомая функция есть функция одной независимой переменной , дифференциальное уравнение называется обыкновенным ; например,
Когда искомая функция есть функция двух и более независимых переменных, например, если , то уравнение вида
называется уравнением в частных производных. Здесь — неотрицательные целые числа, такие, что ; например
Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение. Например, дифференциальное уравнение — уравнение первого порядка, дифференциальное уравнение , где — известная функция, — уравнение второго порядка; дифференциальное уравнение — уравнение 9-го порядка.
Решением дифференциального уравнения n-го порядка на интервале называется функция , определенная на интервале вместе со своими производными до n-го порядка включительно, и такая, что подстановка функции в дифференциальное уравнение превращает последнее в тождество по на . Например, функция является решением уравнения на интервале . В самом деле, дифференцируя функцию дважды, будем иметь
Подставляя выражения и в дифференциальное уравнение, получим тождество
График решения дифференциального уравнения называется интегральной кривой этого уравнения.
Общий вид уравнения первого порядка
Если уравнение (1) удается разрешить относительно , то получится уравнение первого порядка, разрешенное относительно производной.
Задачей Коши называют задачу нахождения решения уравнения , удовлетворяющего начальному условию (другая запись ).
Геометрически это означает, что ищется интегральная кривая, проходящая через заданную точку плоскости (рис. 1).
Теорема существования и единственности решения задачи Коши
Пусть дано дифференциальное уравнение , где функция определена в некоторой области плоскости , содержащей точку . Если функция удовлетворяет условиям
а) есть непрерывная функция двух переменных и в области ;
б) имеет частную производную , ограниченную в области , то найдется интервал , на котором существует единственное решение данного уравнения, удовлетворяющее условию .
Теорема дает достаточные условия существования единственного решения задачи Коши для уравнения , но эти условия не являются необходимыми . Именно, может существовать единственное решение уравнения , удовлетворяющее условию , хотя в точке не выполняются условия а) или б) или оба вместе.
1. . Здесь . В точках оси условия а) и б) не выполняются (функция и её частная производная разрывны на оси и неограниченны при ), но через каждую точку оси проходит единственная интегральная кривая (рис. 2).
2. . Правая часть уравнения и ее частная производная непрерывны по и во всех точках плоскости . В силу теоремы существования и единственности областью, в которой данное уравнение имеет единственное решение
является вся плоскость .
3. . Правая часть уравнения определена и непрерывна во всех точках плоскости . Частная производная обращается в бесконечность при , т.е. на оси , так что при нарушается условие б) теоремы существования и единственности. Следовательно, в точках оси возможно нарушение единственности. Легко проверить, что функция есть решение данного уравнения. Кроме этого, уравнение имеет очевидное решение . Таким образом, через каждую точку оси проходит по крайней мере две интегральные линии и, следовательно, действительно в точках этой оси нарушается единственность (рис. 3).
Интегральными линиями данного уравнения будут также линии, составленные из кусков кубических парабол и отрезков оси , например, и др., так что через каждую точку оси проходит бесконечное множество интегральных линий.
Условие Липшица
Замечание. Условие ограниченности производной , фигурирующее в теореме существования и единственности решения задачи Коши, может быть несколько ослаблено и заменено так называемым условием Липшица .
Говорят, что функция , определенная в некоторой области , удовлетворяет в условию Липшица по , если существует такая постоянная ( постоянная Липшица ), что для любых из и любого из справедливо неравенство
Существование в области ограниченной производной достаточно для того, чтобы функция удовлетворяла в условию Липшица. Напротив, из условия Липшица не вытекает условие ограниченности ; последняя может даже не существовать. Например, для уравнения функция не дифференцируема по в точке , но условие Липшица в окрестности этой точки выполняется. В самом деле,
поскольку а . Таким образом, условие Липшица выполняется с постоянной .
Теорема. Если функция непрерывна и удовлетворяет условию Липшица по в области , то задача Коши
имеет единственное решение.
Условие Липшица является существенным для единственности решения задачи Коши. В качестве примера рассмотрим уравнение
Нетрудно видеть, что функция непрерывна; с другой стороны,
и условие Липшица не удовлетворяется ни в одной области, содержащей начало координат , так как множитель при оказывается неограниченным при .
Данное дифференциальное уравнение допускает решение где — произвольная постоянная. Отсюда видно, что существует бесконечное множество решений, удовлетворяющих начальному условию
Общим решением дифференциального уравнения (2) называется функция
зависящая от одной произвольной постоянной , и такая, что
1) она удовлетворяет уравнению (2) при любых допустимых значениях постоянной ;
2) каково бы ни было начальное условие
можно подобрать такое значение постоянной , что решение будет удовлетворять заданному начальному условию (4). При этом предполагается, что точка принадлежит области, где выполняются условия существования и единственности решения.
Частным решением дифференциального уравнения (2) называется решение, получаемое из общего решения (3) при каком-либо определенном значении произвольной постоянной .
Пример 1. Проверить, что функция есть общее решение дифференциального уравнения и найти частное решение, удовлетворяющее начальному условию . Дать геометрическое истолкование результата.
Решение. Функция удовлетворяет данному уравнению при любых значениях произвольной постоянной . В самом деле,
Зададим произвольное начальное условие . Полагая и в равенстве , найдем, что . Подставив это значение в данную функцию, будем иметь . Эта функция удовлетворяет заданному начальному условию: положив , получим . Итак, функция является общим решением данного уравнения.
В частности, полагая и , получим частное решение .
Общее решение данного уравнения, т.е. функция , определяет в плоскости семейство параллельных прямых с угловым коэффициентом . Через каждую точку плоскости проходит единственная интегральная линия . Частное решение определяет одну из интегральных кривых, а именно прямую, проходящую через начало координат (рис.4).
Пример 2. Проверить, что функция есть общее решение уравнения и найти частное решение, удовлетворяющее начальному условию .
Решение. Имеем . Подставляя в данное уравнение выражения и , получаем , т. е. функция удовлетворяет данному уравнению при любых значениях постоянной .
Зададим произвольное начальное условие . Подставив и вместо и в функцию , будем иметь , откуда . Функция удовлетворяет начальному условию. Действительно, полагая , получим . Функция есть общее решение данного уравнения.
При и получим частное решение .
С геометрической точки зрения общее решение определяет семейство интегральных кривых, которыми являются графики показательных функций; частное решение есть интегральная кривая, проходящая через точку (рис.5).
Соотношение вида , неявно определяющее общее решение, называется общим интегралом дифференциального уравнения первого порядка.
Соотношение, получаемое из общего интеграла при конкретном значении постоянной , называется частным интегралом дифференциального уравнения.
Задача решения или интегрирования дифференциального уравнения состоит в нахождении общего решения или общего интеграла данного дифференциального уравнения. Если дополнительно задано начальное условие, то требуется выделить частное решение или частный интеграл, удовлетворяющие поставленному начальному условию.
Так как с геометрической точки зрения координаты и равноправны, то наряду с уравнением мы будем рассматривать уравнение .
Дифференциальные уравнения (ДУ) — методы и примеры решения уравнений разного порядка
Многих людей, хоть как-то изучавших курс высшей математики в учебном заведении, приводит в ужас словосочетание «дифференциальные уравнения». Согласно строгому научному определению в книгах – так именуются математические выражения, где в состав входят функция, ее производная или параметр. Имеется достаточно большое количество типов этих равенств, рассмотрим подходы к их решению так, чтобы они были понятны даже для «чайников».
Дифференциальные уравнения первого порядка
Обыкновенное диффуравнение (ДУ) 1-го порядка задается относительно некой функции, имеющей вид у(х):
здесь, F(x,y,y ’ ) – это функция, задающаяся для трех аргументов (в этом примере для х, у и у ’ ).Таково строгое математическое определение ДУ.
Для примера можно привести следующее уравнение:
функция вида F(x,y,p) = xp — y 2
Простейшие ДУ первого порядка
Общепринятый механизм нахождения решения таких выражений (чаще всего похожи на y’ = f(x)) – это интегрирование левой и правой части такого уравнения на заданном промежутке Х.
После интегрирования получим такое выражение:
Воспользовавшись свойствами, которые относятся к интегральным выражениям, упростим выражение до вида:
здесь, F(x) – это первообразная от функции f(x) на заданном интервале Х, а N – случайным образом выбранная константа.
Задача №1
Необходимо определить все возможные варианты решения диффуравнения, имеющего вид
Последовательно рассмотрим решение.
Представленное диффуравнение может иметь смысл только при действительных значениях параметра х. Примем условие, что x ≠ 0, тогда выражение легко преобразовывается в следующее:
Если же, напротив, принять, что х = 0, то выражение приобретет следующий вид, характерный для любых функций y’, удовлетворяющих данному условию:
Можно заключить, что решением при справедливости условия х = 0 будет любая функция у, найденная, когда аргумент равен нулю. Остается только проинтегрировать полученное диффуравнение:
Данное выражение – это решение для приведенного диффуравнения.
ДУ с разделяющимися переменными
Среди дифуров 1-го порядка можно выделить такие, где все переменные х и у можно преобразовать так, что они окажутся по разные стороны от знака равенства.
Соответственно уравнения, где путем преобразований это возможно сделать, называются диффуравнениями с разделяющимися переменными.
Их общий вид следующий:
После проведения нескольких преобразований, это выражение может быть сведено к следующему виду:
При составлении преобразований необходимо внимательно разделять переменные, не допуская, чтобы функции обращались в ноль, иначе возможна потеря некоторых значений.
Задача №2
Рассмотрим обыкновенный пример. Необходимо определить все возможные решения диффуравнения y’ = y(x 2 + e x )
Как решать? В первую очередь проводим разделение переменных в разные части уравнения:
Данные преобразования справедливы, если у ≠ 0.
Если рассмотреть вариант решения при нулевом показателе функции, то можно заметить ,что
Это означает, что y = 0 – одно из возможных решений задачи.
Рассмотрим другие варианты решений, для чего произведем интегрирование диффуравнения:
Финальная часть преобразований будет вторым решением диффуравнения. Останется только потенциировать это выражение, чтобы привести его к более явному виду:
Правильными решениями, в результате преобразований, будут:
Кроме того, можно воспользоваться онлайн системой для нахождения ответа. Подробные объяснения даны в решебниках Филиппова и Понтрягина.
Линейные неоднородные ДУ первого порядка
Линейные неоднородные уравнения – это такие выражения, которые можно записать в формате y’ + b(x)y = f(x), при этом функции b(x) и f(x) – непрерывные.
Основной принцип при нахождении решения сводится к следующим шагам:
Первым делом для уравнения необходимо произвести поиск решения, которое бы соответствовало линейному однородному диффуравнению.
Затем необходимо варьировать произвольной постоянной, производя ее замену на функцию.
На финальном этапе функция подставляется в первоначальное уравнение, откуда, решая ДУ, получается ответ.
Задача №3
Рассмотрим применение методики решения на примере.
Необходимо найти решение дифференциального уравнения вида
Решение заключается в следующем. Первоначально примем, что y = m∗n, следовательно, получается:
На следующем этапе нужно определить, что такое m (оно обязательно не должно быть равным нулю), при котором все выражение внутри скобок будет равно нулю.
Получаем дополнительное дифференциальное уравнение:
Теперь необходимо принять одно из частных решений n = x 2 + 1, которое соответствует равенству С2 — С1=0.
Выполняем оставшиеся преобразования:
Вполне очевидно, что ответом на условие задачи будет функция:
Задача Коши для ДУ
При рассмотрении решения практически любого диффуравнения, имеющего вид F(m,n,n’) = 0, становится очевидно, что это бесконечно большое количество решений (это следствие самого возникновения диффуравнения).
На данном этапе математики сталкиваются с вопросом о выборе конкретного решения и способе его выделения из множества.Иными словами, если представить решения в виде бесконечного множества интегральных кривых, то необходимо найти среди них нужную.
Чтобы это сделать, необходимо рассмотреть плоскость Xoy, где должна быть задана некая точка D0, имеющая координаты (x0, y0) – именно через них и должна пройти интегральная кривая, чтобы стать искомым ответом.
Когда мы с самого начала задаем точку D0(x0, y0) – это означает, задание начального условия y(x0) = y0. Диффуравнение, для которого определено начальное условие в представленном формате, называется уравнением с заданной задачей Коши.
Задача №4
Рассмотрим примеры с объяснениями. Необходимо определить решения задачи Коши вида:
Ход решения строится в три этапа. На первом этапе решаем диффуравнение y’ = xy 2 стандартным методом. Его решение приводить не будем, приведем только ответ:
Производим подстановку начального значения (х = 0, у = 1) в решение и находим значение С:
Производим подстановку полученного значения в ответ диффуравнения и получаем одно из частных решений:
Полученная функция – ответ на задачу Коши в этом примере.
Дифференциальные уравнения Бернулли
ДУ Бернулли обычно представлено в следующем виде:
Обязательное условие, что функции b(x) и c(x) – являются непрерывными.
Задача №5
Рассмотрим общее решение данного типа на примере. Необходимо выполнить поиск всех возможных решений уравнения:
Во время оценки уравнения в нем можно идентифицировать ДУ Бернулли с параметром ½. Оно легко сводится к линейному ДУ, для этого достаточно заменить выражения:
Выполним деление по начальному уравнению Бернулли на
и выполним необходимые преобразования:
Произведем замену параметра х на параметр у:
Теперь вычисляем интегрирующий модуль для данной функции, он будет равен:
Теперь производим ряд преобразований для вычисления решения диффуравнения:
Переписываем полученную функцию в неявном виде и получаем ответ:
Дифференциальные уравнения второго порядка
Отличить ДУ 2-го порядка от таковых 1-го порядка достаточно просто – в их составе присутствует вторая производная (y’’) и не содержится производных более высокого уровня.
Общий вид таких уравнений таков:
Линейные однородные ДУ второго порядка с постоянными коэффициентами
Определение линейных дифференциальных однородных уравнений 2-го порядка крайне просто – они имеют вид:
При это важным условием теории является причисление r и k к действительным числам.
Задача №6
Рассмотрим решение однородных диффуравнений 2-го порядка с постоянными коэффициентами на примере.
Найти решение диффуравнения 2-го порядка вида:
Во всех таких случаях начинаем с поиска характеристического уравнения:
Методы решения данного уравнения достаточно простые, можно воспользоваться калькулятором или быстро решить на листочке, поэтому их приводить не будем, запишем лишь корни – 1, 5.
Поскольку это все действительные, неодинаковые числа, то можно записать функцию-решение в следующем виде:
Линейные неоднородные ДУ второго порядка с постоянными коэффициентами
Общий вид неоднородных диффуравнений второго порядка легко определить по представленному образцу:
Переменные r и k должны быть вещественными и постоянными числами.
Задача №7
Рассмотрим подробное решение. Необходимо определить все решения для уравнения y» + y = cos x.
На первом этапе находим в составе неоднородного уравнения его однородную часть – это будет y» — y = 0.
Для него уже выполняем поиск характеристического уравнения – оно будет иметь вид k 2 + 1 = 0.
Корнями для данного характеристического уравнения являются k1 = -i и k2 = i.
Исходя из этого записываем решение для однородного уравнения:
Из-за отсутствия параметра с производной первого порядка также будет справедливо записать:
Теперь остается только подставить найденные выражения:
Частное и общее решение для уравнения можно записать:
Дифференциальные уравнения высших порядков
Дифференциальные однородные уравнения высших порядков легко отличить, если они совпадают со следующим видом:
Для неоднородных справедлив другой формат:
Для выбора корректного пути решения ДУ, необходимо четко и правильно определить его тип.
Для этого необходимо решить уравнение относительно его производной и проверить, возможно ли разложение функции на множители. После этого достаточно сравнить с одним из типов, приведенным в данной статье.
http://mathhelpplanet.com/static.php?p=osnovnye-ponyatiya-i-opredeleniya-differentsialnyh-uravneniy
http://nauka.club/matematika/algebra/differentsialnye-uravneniya.html