Две пересекающиеся прямые каноническое уравнение

Уравнение плоскости, которая проходит через две пересекающиеся или две параллельные прямые

В данном материале мы расскажем, как правильно вычислить уравнение плоскости, которая проходит через 2 пересекающиеся или параллельные прямые. Начнем с формулировки основного принципа, а потом, как всегда, разберем несколько задач, где можно применить этот принцип на практике.

Как найти уравнение плоскости, проходящей через пересекающиеся прямые?

Для того чтобы вывести это уравнение, нам понадобится вспомнить одну теорему. Она звучит так:

Через две пересекающиеся прямые может проходить только одна плоскость.

Доказательство этого утверждения основано на двух аксиомах:

1. через три точки с разными координатами, которые не лежат на одной прямой, проходит только одна плоскость;
2. если у нас есть две точки прямой с разными координатами, расположенные в некоторой плоскости, то все точки этой прямой находятся в этой плоскости.

В итоге мы можем утверждать, что с помощью указания двух пересекающихся прямых мы можем задать определенную плоскость в трехмерном пространстве.

Далее нам нужно доказать, что плоскость, которая проходит через две определенные прямые, совпадет с той, что проходит через три заданные точки, две из которых находятся на тех самых прямых.

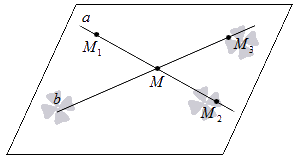
Допустим, у нас есть две прямые a и b с пересечением в некой точке M . Теперь расположим на первой прямой две точки М 1 и М 2 . У них должны быть разные координаты, но при этом одна из них может совпадать с точкой пересечения. На второй прямой отметим точку М 3 (но она совпадать с точкой M не должна). Теперь нам надо показать, что плоскость, проходящая через М 1 М 2 М 3 , – это та же самая плоскость, что проходит через пересекающиеся прямые a и b .

Посмотрим на схему:

Поскольку мы имеем точки прямой a , которые находятся в плоскости М 1 М 2 М 3 ( М 1 и М 2 ), то, используя аксиому, которую мы приводили выше, можно утверждать, что все точки этой прямой находятся в данной плоскости. Все точки прямой b тоже будут находиться в ней, поскольку там расположены две несовпадающие точки данной прямой ( М и М 3 ). Таким образом, мы доказали, что плоскости, в которых лежат данные прямые, совпадают.

Теперь перейдем непосредственно к формулировке уравнения плоскости, которая проходит через пересекающиеся прямые. Возьмем a и b , которые заданы в прямоугольной системе координат O x y z в трехмерном пространстве и являются пересекающимися. Напишем уравнение плоскости, которая проходит через эти прямые.

Все решение можно свести к нахождению уже изученного уравнения плоскости, проходящей через три точки. Сначала нам надо найти координаты двух точек M 1 и M 2 , которые расположены на пересекающихся прямых, и точки M 3 , которая находится на другой прямой и не является точкой их пересечения. Для этого можно использовать разные способы. Так, мы можем составить параметрические уравнения для первой прямой в пространстве. В итоге получим:

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ

Отсюда можно вывести координаты x 1 , y 1 , z 1 точки M 1 , если λ = 0 . Для М 2 эти данные можно вычислить, если придать параметру любое действительное значение, отличное от нуля, например, единицу.

Далее мы можем составить такие же параметрические уравнения для второй прямой и, используя некоторое значение параметра, высчитать координаты М 3 . Важно проверить, чтобы она не лежала в точке пересечения прямых и вообще не находилась на прямой a .

Итак, мы нашли координаты всех нужных точек – М 1 , М 2 и М 3 . Переходим к написанию уравнения плоскости, которая через них проходит. Запишем:

x — x 1 y — y 1 z — z 1 x 2 — x 1 y 2 — y 1 z 2 — z 1 x 3 — x 1 y 3 — y 1 z 3 — z 1 = 0

Теперь найдем определитель матрицы x — x 1 y — y 1 z — z 1 x 2 — x 1 y 2 — y 1 z 2 — z 1 x 3 — x 1 y 3 — y 1 z 3 — z 1 и получим общее уравнение для нужной нам плоскости, которая будет проходит через две заданные прямые a и b .

Как найти уравнение плоскости, проходящей через параллельные прямые?

Для этого нам понадобится вспомнить теорему, которая формулируется так:

Через две параллельные прямые проходит только одна плоскость.

Ее можно доказать, используя аксиому о единственной плоскости, которая проходит через три точки, а также утверждение о двух параллельных прямых (если одна из параллельных прямых пресекает некоторую плоскость, то это же делает и другая).

Итак, возможно задать плоскость в пространстве, если указать две параллельные прямые, которые в ней находятся.

Очевиден тот факт, что плоскость, которая проходит через 2 параллельные прямые и плоскость, которая проходит через три точки, две из которой лежат на одной из этих прямых, будут совпадать.

После этого мы можем найти уравнение плоскости, проходящей через две заданные параллельные прямые.

У нас есть прямоугольная система координат в трехмерном пространстве, которая обозначается O x y z . Составим уравнение плоскости, которая проходит через параллельные прямые a и b .

Сводим задачу опять же к нахождению уравнения для плоскости с тремя точками. В самом деле, можно определить, какие точно координаты будут иметь М 1 и М 2 , лежащие на одной из параллельных прямых, и М 3 , расположенная на другой прямой. После этого просто запишем нужное нам уравнение для плоскости, проходящей через три точки M 1 ( x 1 , y 1 , z 1 ) , M 2 ( x 2 , y 2 , z 2 ) , M 3 ( x 3 , y 3 , z 3 ) в следующем виде:

x — x 1 y — y 1 z — z 1 x 2 — x 1 y 2 — y 1 z 2 — z 1 x 3 — x 1 y 3 — y 1 z 3 — z 1 = 0

Это и есть нужное нам уравнение плоскости, проходящей через заданные параллельные прямые.

Примеры задач на нахождение подобных уравнений

Таким образом, для того чтобы составить уравнение плоскости, которая проходит через 2 пересекающиеся или параллельные прямые, требуется вычислить координаты трех точек, которые расположены на этих прямых (две точки на одной прямой и третья на другой). Посмотрим, как это принцип реализуется на практике.

У нас задана прямоугольная система координат в трехмерном пространстве. Расположенная в ней прямая a проходит через точку M 1 ( — 3 , 1 , — 4 ) и пересекает координатную прямую O y в точке M 2 ( 0 , 5 , 0 ) . Составьте уравнение плоскости, которая будет проходить через пересекающиеся a и O y .

Решение

Изначально у нас заданы координаты двух точек, которые расположены на исходной прямой. Для составления уравнения нам нужна третья. Возьмем точку начала координат O ( 0 , 0 , 0 ) . Она расположена на O y и не совпадает с координатами двух точек, которые были заданы в условии. Та плоскость, что будет проходить через них, и есть та, для которой нам надо вывести уравнение. Запишем его в координатном виде:

x — x 1 y — y 1 z — z 1 x 2 — x 1 y 2 — y 1 z 2 — z 1 x 3 — x 1 y 3 — y 1 z 3 — z 1 = 0 ⇔ x — 0 y — 0 z — 0 — 3 — 0 1 — 0 — 4 — 0 0 — 0 5 — 0 0 — 0 = 0 ⇔ ⇔ x y z — 3 1 — 4 0 5 0 = 0 ⇔ 20 x — 15 z = 0 ⇔ 4 x — 3 z = 0

Ответ: 4 x — 3 z = 0 .

Возьмем более сложный пример, где координаты нужных точек не будут столь очевидными.

У нас есть две пересекающиеся прямые a и b , которые заданы с помощью уравнений.

x — 7 4 = y — 7 5 = z + 5 — 6 x — 3 1 = y — 2 — 3 = z — 1 5

Составьте уравнение плоскости, которая проходит через них.

Решение

Начнем с вычисления координат трех необходимых точек. Две из них расположены на прямой a , третья – на b .

Прямая в условии задана с помощью канонических уравнений в пространстве вида x — 7 4 = y — 7 5 = z + 5 — 6 , следовательно, она будет проходить через точку x — 7 4 = y — 7 5 = z + 5 — 6 .

Для вычисления координат второй точки нам надо записать параметрическое уравнение:

x — 7 4 = y — 7 5 = z + 5 — 6 ⇔ x = 7 + 4 · λ y = 7 + 5 · λ z = — 5 — 6 · λ

Если мы примем λ = 1 , то сможем подсчитать координаты второй точки:

x = 7 + 4 · λ y = 7 + 5 · λ z = — 5 — 6 · λ ⇔ x = 11 y = 12 z = — 11

Мы получили, что M 2 ( 11 , 12 , — 11 ) .

Понятно, что прямая, заданная с помощью уравнения x — 3 1 = y — 2 — 3 = z — 1 5 , будет проходить через точку M 3 ( 3 , 2 , 1 ) . Перед вычислениями надо проверить, не лежит ли она в точке пересечения прямых. Для этого надо подставить ее координаты во второе уравнение:

3 — 7 4 = 2 — 7 5 = 1 + 5 — 6 ⇔ — 1 ≡ — 1 ≡ — 1

Мы видим, что канонические уравнения прямой свелись к тождествам. Тогда наша третья точка лежит именно в месте пересечения прямых, значит, нам надо взять еще одну, которая будет находится на прямой b . Для этого также запишем параметрические уравнения:

x — 3 1 = y — 2 — 3 = z — 1 5 ⇔ x = 3 + μ y = 2 — 3 · μ z = 1 + 5 · μ

Высчитаем нужные координаты, приняв μ = 1 .

x = 3 + 1 y = 2 — 3 · 1 z = 1 + 5 · 1 ⇔ x = 4 y = — 1 z = 6 ⇔ M 3 ( 4 , — 1 , 6 )

Далее мы можем переходить непосредственно у формулированию уравнения нужной нам плоскости, которая будет проходить через M 1 ( 7 , 7 , — 5 ) , M 2 ( 11 , 12 , — 11 ) , M 3 ( 4 , — 1 , 6 ) :

x — x 1 y — y 1 z — z 1 x 2 — x 1 y 2 — y 1 z 2 — z 1 x 3 — x 1 y 3 — y 1 z 3 — z 1 = 0 ⇔ x — 7 y — 7 z — ( — 5 ) 11 — 7 12 — 7 — 11 — ( — 5 ) 4 — 7 — 1 — 7 6 — ( — 5 ) = 0 ⇔ ⇔ x — 7 y — 7 z + 5 4 5 — 6 — 3 — 8 11 = 0 ⇔ 7 x — 26 y — 17 z + 48 = 0

Ответ: 7 x — 26 y — 17 z + 48 = 0 .

Очевидно, что процесс вычисления координат нужных нам точек занимает больше всего времени при решении подобных задач.

Нам осталось разобрать пример плоскости, которая проходит через две прямые, являющиеся параллельными.

Составьте уравнение плоскости, которая проходит через две параллельные прямые. Они выражены с помощью уравнений x = 2 · λ y = 1 + λ z = — 1 — λ и x — 3 2 = y 1 = z + 5 — 1 .

Решение

Вычисляем координаты двух нужных точек по параметрическим уравнениям, приняв λ = 0 и λ = 1 .

λ = 0 : x = 2 · 0 y = 1 + 0 z = — 1 — 0 ⇔ x = 0 y = 1 z = — 1 ⇔ M 1 ( 0 , 1 , — 1 ) λ = 1 : x = 2 · 1 y = 1 + 1 z = — 1 — 1 ⇔ x = 2 y = 2 z = — 2 ⇔ M 2 ( 2 , 2 , — 2 )

У нас получается, что прямая x — 3 2 = y 1 = z + 5 — 1 будет проходить через точку M 3 ( 3 , 0 , — 5 ) .

Переходим к уравнению плоскости для трех точек М 1 , М 2 и М 3 :

x — x 1 y — y 1 z — z 1 x 2 — x 1 y 2 — y 1 z 2 — z 1 x 3 — x 1 y 3 — y 1 z 3 — z 1 = 0 ⇔ x — 0 y — 1 z — ( — 1 ) 2 — 0 2 — 1 — 2 — ( — 1 ) 3 — 0 0 — 1 — 5 — ( — 1 ) = 0 ⇔ ⇔ x y — 1 z + 1 2 1 — 1 3 — 1 — 4 = 0 ⇔ — 5 x + 5 y — 5 z — 10 = 0 ⇔ x — y — z + 2 = 0

Ответ: x — y — z + 2 = 0 .

Кривые второго порядка. Канонический вид уравнений второго порядка.

Кривая второго порядка — геометрическое место точек на плоскости, прямоугольные координаты

которых удовлетворяют уравнению вида:

в котором, по крайней мере один из коэффициентов a₁₁, a₁₂, a₂₂ не равен нулю.

Инварианты кривых второго порядка.

Вид кривой зависим от 4 инвариантов, приведенных ниже:

— инварианты относительно поворота и сдвига системы координат:

— инвариант относительно поворота системы координат (полуинвариант):

Для изучения кривых второго порядка рассматриваем произведение А*С.

Общее уравнение кривой второго порядка выглядит так:

Ax 2 +2Bxy+Cy 2 +2Dx+2Ey+F=0

— Если А*С > 0, то уравнение принимает вид уравнения эллиптического типа. Любое эллиптическое

уравнение – это уравнение или обычного эллипса, или же вырожденного эллипса (точки), или мнимого

эллипса (в таком случае уравнение не определяет на плоскости ни одного геометрического образа);

уравнение выражает или простую гиперболу, или вырожденную гиперболу (две пересекающиеся прямые);

— Если А*С = 0, то линия второго порядка не будет центральной. Уравнения такого типа называют

уравнениями параболического типа и выражают на плоскости или простую параболу, или 2 параллельных

(либо совпадающих) прямых, или не выражают на плоскости ни одного геометрического образа;

— Если А*С ≠ 0, кривая второго порядка будет центральной;

Таким образом, виды кривых второго порядка:

Канонический вид уравнений второго порядка.

Вводя новую систему координат можно привести уравнения кривых второго порядка к стандартному

каноническому виду. Характеристики канонических уравнений очень легко выражаются через инварианты

Δ, D, I и корни характеристического уравнения .

Исследование уравнений второго порядка

Преобразование координат в уравнении второго порядка.

В общей декартовой системе координат линия второго порядка может быть задана уравнением
$$
Ax^ <2>+ 2Bxy + Cy^ <2>+ 2Dx + 2Ey + F = 0,\label
$$
в котором коэффициенты \(A\), \(B\) и \(C\) не равны нулю одновременно. Исследуем множество точек, которые ему удовлетворяют, не предполагая заранее, что хоть одна такая точка существует. С этой целью мы будем менять систему координат так, чтобы уравнение стало возможно проще. С самого начала можно считать систему координат декартовой прямоугольной, так как при переходе к прямоугольной системе координат общий вид уравнения \eqref не изменится.

При повороте базиса декартовой прямоугольной системы координат на угол \(\varphi\) старые координаты точки \(x\), \(y\) будут связаны с ее новыми координатами \(x’\), \(y’\) формулами
$$
x = x’\cos \varphi-y’\sin \varphi,\\ y = x’\sin \varphi + y’\cos \varphi.\nonumber
$$
В новых координатах уравнение \eqref примет вид
$$
A(x’\cos \varphi-y’\sin \varphi)^ <2>+ 2B(x’\cos \varphi-y’\sin \varphi) \times \\ \times (x’\sin \varphi + y’\cos \varphi) + C(x’\sin \varphi + y’\cos \varphi) + … = 0.\nonumber
$$
Здесь многоточием обозначены члены первой степени относительно \(x’\), \(y’\) и свободный член, которые нет необходимости выписывать. Нас будет интересовать член с произведением \(x’y’\) в преобразованном уравнении. В невыписанные члены это произведение не входит, и мы подсчитаем, что половина коэффициента при \(x’y’\) есть
$$
B’ = -A\sin \varphi \cos \varphi + B(\cos^<2>\varphi-\sin^<2>\varphi) + C\sin \varphi \cos \varphi.\nonumber
$$
Если \(B = 0\), то поворачивать систему координат не будем. Если же \(B \neq 0\), то выберем угол \(\varphi\) так, чтобы \(B’\) обратилось в нуль.

Это требование приведет к уравнению
$$
2B \cos 2\varphi = (A-C)\sin 2\varphi.\label
$$
Если \(A = C\), то \(\cos 2\varphi = 0\), и можно положить \(\varphi = \pi/4\). Если же \(A \neq C\), то выбираем \(\varphi = \displaystyle\frac<1> <2>\operatorname \left[\frac<2B>\right]\). Для нас сейчас важно то, что хоть один такой угол обязательно существует. После поворота системы координат на этот угол линия будет иметь уравнение
$$
A’x’^ <\ 2>+ C’y’^ <\ 2>+ 2D’x’ + 2E’y’ + F’ = 0.\label
$$
Выражения для коэффициентов уравнения \eqref через коэффициенты \eqref подсчитать не трудно, но это не нужно. Теперь коэффициент при произведении переменных равен нулю, а остальные члены мы по-прежнему считаем произвольными.

Если в уравнение \eqref входит с ненулевым коэффициентом квадрат одной из координат, то при помощи переноса начала координат вдоль соответствующей оси можно обратить в нуль член с первой степенью этой координаты.

В самом деле, пусть, например, \(A’ \neq 0\). Перепишем \eqref в виде
$$
A’\left(x’^ <\ 2>+ \frac<2D’>x’ + \frac>>\right) + C’y’^ <\ 2>+ 2E’y’ + F’-\frac = 0.\nonumber
$$
Если мы сделаем перенос начала координат, определяемый формулами \(x″ = x’ + D’/A’\), \(y″ = y’\), то уравнение приведется к виду
$$
A’x″^ <\ 2>+ C’y″^ <\ 2>+ 2E’y″ + F″ = 0,\nonumber
$$
как и требовалось.

Канонические виды уравнений второго порядка.

Предположим, что \(A’C’ \neq 0\), то есть оба коэффициента отличны от нуля. Согласно утверждению 1 при помощи переноса начала координат уравнение приведется к виду
$$
A’x″^ <\ 2>+ C’y″^ <\ 2>+ F″ = 0.\label
$$

Могут быть сделаны следующие предположения относительно знаков коэффициентов в этом уравнении.

Случай A’C’ > 0.

Если \(A’C’ > 0\), то коэффициенты \(A’\) и \(C’\) имеют один знак. Для \(F″\) имеются следующие три возможности.

Знак \(F″\) противоположен знаку \(A’\) и \(C’\). Перенесем \(F″\) в другую часть равенства и разделим на него. Уравнение примет вид
$$
\frac>> + \frac>> = 1,\label
$$
где \(a^ <2>= -F″/A’\), \(b^ <2>= -F″/C’\). Можно считать, что в этом уравнении \(a > 0\), \(b > 0\) и \(a \geq b\). Действительно, если последнее условие не выполнено, то можно сделать дополнительную замену координат
$$
x^ <*>= y″,\ y^ <*>= x″.\label
$$

Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением \eqref при условии \(a \geq b\), называется эллипсом, уравнение называется каноническим уравнением эллипса, а система координат — его канонической системой координат.

При \(a = b\) уравнение \eqref есть уравнение окружности радиуса \(a\). Таким образом, окружность — частный случай эллипса.

Случай A’C’ Определение.

Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением \eqref, называется гиперболой, уравнение называется каноническим уравнением гиперболы, а система координат — ее канонической системой координат.

Случай \(A’C’ = 0\).

Допустим теперь, что \(A’C’ = 0\), и, следовательно, один из коэффициентов \(A’\) или \(C’\) равен нулю. В случае необходимости, делая замену \eqref, мы можем считать, что \(A’ = 0\). При этом \(C \neq 0\), так как иначе порядок уравнения был бы меньше двух. Используя утверждение 1, мы приведем уравнение к виду
$$
C’y″^ <\ 2>+ 2D’x″ + F″ = 0.\nonumber
$$

Пусть \(D’ \neq 0\). Сгруппируем члены следующим образом:
$$
C’y″^ <\ 2>+ 2D’\left(x″ + \frac<2D’>\right) = 0.\nonumber
$$
Перенесем начало координат вдоль оси абсцисс в соответствии с формулами перехода \(x^ <*>= x″ + F″/2D’\), \(y^ <*>= y″\). Тогда уравнение примет вид
$$
C″y^ <*2>+ 2D’x^ <*>= 0,\nonumber
$$
или
$$
y^ <*2>= 2px^<*>,\label
$$
где \(p = -D’/C″\). Мы можем считать, что \(p > 0\), так как в противном случае можно сделать дополнительную замену координат, изменяющую направление оси абсцисс: \(\tilde = -x^<*>\), \(\tilde = y^<*>\).

Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением \eqref при условии \(p > 0\), называется параболой, уравнение называется каноническим уравнением параболы, а система координат — ее канонической системой координат.

Допустим, что \(D’ = 0\). Уравнение имеет вид \(C’y″^ <\ 2>+ F″ = 0\). Относительно \(F″\) есть следующие три возможности.

1. Если \(C’F″ 0\) знаки \(C’\) и \(F″\) совпадают. Разделив на \(C’\), приведем уравнение к виду
   $$
   y″^ <\ 2>+ a^ <2>= 0.\label
   $$
   Этому уравнению не удовлетворяют координаты ни одной точки. Уравнение, приводящееся к каноническому виду \eqref, называют уравнением пары мнимых параллельных прямых.
2. Остался последний случай \(F″ = 0\). После деления на \(C’\) уравнение принимает вид
   $$
   y″^ <\ 2>= 0.\label
   $$
   Это уравнение эквивалентно уравнению \(y″ = 0\), и потому определяет прямую линию. Уравнение, приводящееся к каноническому виду \eqref, называется уравнением пары совпавших прямых.

Теперь мы можем объединить всё вместе.

Пусть в декартовой системе координат задано уравнение второго порядка \eqref.

Тогда существует такая декартова прямоугольная система координат, в которой это уравнение принимает один из следующих девяти канонических видов:

1. Уравнение эллипса.
   $$
   \frac>> + \frac>> = 1;\nonumber
   $$
2. Мнимый эллипс. Данному уравнению не удовлетворяет ни одна точка.
   $$
   \frac>> + \frac>> = -1;\nonumber
   $$
3. Уравнение пары мнимых пересекающихся прямых (точка).
   $$
   a^<2>x^ <2>+ c^<2>y^ <2>= 0;\nonumber
   $$
4. Уравнение гиперболы.
   $$
   \frac>>-\frac>> = 1;\nonumber
   $$
5. Пересекающиеся прямые.
   $$
   a^<2>x^<2>-c^<2>y^ <2>= 0;\nonumber
   $$
6. Уравнение параболы.
   $$
   y^ <2>= 2px;\nonumber
   $$
7. Пара параллельных прямых.
   $$
   y^<2>-a^ <2>= 0;\nonumber
   $$
8. Пара мнимых параллельных прямых. Данному уравнению не удовлетворяет ни одна точка.
   $$
   y^ <2>+ a^ <2>= 0;\nonumber
   $$
9. Прямая (пара совпавших прямых).
   $$
   y^ <2>= 0.\nonumber
   $$