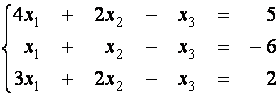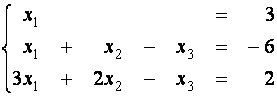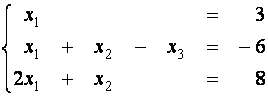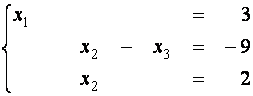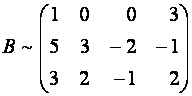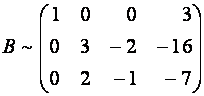Равносильные системы уравнений, равносильные преобразования
В этой статье мы поговорим про равносильные системы уравнений. Здесь мы дадим соответствующее определение, а также разберем, какие существуют преобразования, позволяющие переходить от исходной системы уравнений к равносильной ей системе.
Навигация по странице.
Определение равносильных систем уравнений
В учебниках [1, с. 199; 2, с. 74] дается определение равносильных систем уравнений с двумя переменными:
Две системы уравнений с двумя переменными называются равносильными, если они имеют одни и те же решения или если обе системы не имеют решений.
В старших классах оно обобщается на системы с любым числом уравнений и переменных [3, с. 265] :
Две системы уравнений называются равносильными, если они имеют одни и те же решения или если обе системы не имеют решений.
Примеры равносильных и неравносильных систем приведем в следующем пункте.
Равносильны ли данные системы уравнений?
Чтобы сделать вывод о равносильности или неравносильности данных систем уравнений на основе определения, надо наперед знать решения этих систем. Приведем пример. Пусть нам известно, что системы уравнений 

Чтобы доказать неравносильность систем уравнений, достаточно привести одно частное решение, являющееся решением одной системы, но не являющееся решением другой. Например, легко обосновать, что системы уравнений 

А как доказать равносильность систем уравнений, если их решения неизвестны? Конечно, можно найти решения, после чего сделать вывод касательно равносильности на основе определения. Но иногда для этого решать системы необязательно, это касается тех случаев, когда видно, что одна система получена из другой при помощи некоторых так называемых равносильных преобразований. Их мы подробно изучим в следующем пункте, а пока приведем пример.
Рассмотрим две системы уравнений 

Равносильные преобразования систем уравнений
Существует ряд преобразований, позволяющих преобразовать данную систему уравнений в равносильную ей систему. Они получили название равносильных преобразований, и нашли основное применение при решении систем уравнений. Эти преобразования можно считать свойствами систем уравнений. Рассмотрим и обоснуем основные из них.
Перестановка местами уравнений системы дает равносильную систему уравнений.
Доказательство этого утверждения очевидно. В силу определения решения системы уравнений любое отдельно взятое решение системы уравнений является решением каждого уравнения этой системы. Понятно, что оно является и решением каждого уравнения системы с этими же уравнениями, но переставленными местами, значит, является решением и системы с переставленными местами уравнениями.
К примеру, 

Если любое уравнение в системе заменить равносильным уравнением, то полученная система будет равносильна исходной.
Доказательство этого факта тоже лежит на поверхности. Любое решение системы уравнений является решением каждого уравнения системы. Мы также знаем, что равносильные уравнения имеют одинаковые решения. Поэтому, любое решение исходной системы уравнений будет решением всех уравнений системы, в которой какое-то уравнение заменено равносильным ему уравнением, а значит, и решением этой системы.
Важность доказанного свойства огромна: оно дает нам право на работу с отдельными уравнениями системы. С ними мы можем проводить всевозможные уже знакомые нам равносильные преобразования, например, перестановку местами слагаемых, перенос слагаемых из одной части в другую с противоположным знаком, умножение или деление обеих частей уравнения на отличное от нуля число и т.д.
Приведем пример. Пусть дана система 

Если к левой и правой части одного из уравнений системы прибавить соответственно левую и правую часть другого уравнения системы, то полученная система будет равносильна исходной.
Для доказательства покажем, что любое решение изначальной системы уравнений является решением полученной, и обратно, что любое решение полученной системы является решением исходной. Это будет означать равносильность систем.
Любое решение начальной системы является решением каждого ее уравнения, оно обращает все уравнения в верные числовые равенства. Нам известно свойство числовых равенств, которое утверждает, что при почленном сложении верных числовых равенств получается верное равенство. Отсюда следует, что взятое нами решение начальной системы является решением уравнения, полученного в результате почленного прибавления к нему другого уравнения. Поэтому, это решение является решением и полученной системы уравнений, так как является решением каждого ее уравнения.
Теперь обратно. Возьмем любое решение полученной системы, оно является решением каждого ее уравнения, то есть, оно обращает их в верные числовые равенства. Существует свойство, позволяющее выполнять почленное вычитание верных числовых равенств. Вычтем из равенства, соответствующего уравнению, полученному в результате почленного сложения, равенство, соотетствующее прибавленному ранее уравнению. Это даст верное числовое равенство, отвечающее начальному уравнению системы до прибавления к нему другого уравнения. Отсюда следует, что взятое решение будет решением каждого уравнения исходной системы, а значит, и ее решением.
Приведем пример выполнения этого равносильного преобразования. Возьмем систему двух уравнений с двумя переменными 

Понятно, что если система содержит три или большее число уравнений, то можно не ограничиваться почленным прибавлением к левой и правой части выбранного уравнения левой и правой части одного уравнения, а прибавлять левые и правые части двух, трех, да хоть всех остальных уравнений системы. В результате этих действий все равно получится равносильная система уравнений.
На доказанном равносильном преобразовании базируется один из методов решения систем уравнений – метод алгебраического сложения.
Если одно из уравнений системы представляет собой переменную, выраженную через другие переменные, то в любое другое уравнение системы можно подставить вместо этой переменной ее выражение, система, полученная в результате такого преобразования, равносильна исходной.
Приведем пример для пояснения. Возьмем систему 

Пусть пара (x0, y0) – решение исходной системы, тогда x0=2·y0−1 и x0+3·y0−1=0 – верные числовые равенства. Докажем, что при этом равенство (2·y0−1)+3·y0−1=0 тоже верное, что будет доказывать, что (x0, y0) является решением системы, полученной после преобразования, а это будет означать, что полученная система имеет те же решения, что и исходная.
Легко показать, что при условии x0=2·y0−1 значения выражений x0+3·y0−1 и (2·y0−1)+3·y0−1 равны. Для этого составим их разность и покажем, что она равна нулю: x0+3·y0−1−((2·y0−1)+3·y0−1)= (x0−(2·y0−1))+(3·y0−1−(3·y0−1))= x0−(2·y0−1) , а полученное выражение равно нулю в силу равенства x0=2·y0−1 . Итак, справедливо равенство x0+3·y0−1=(2·y0−1)+3·y0−1 , но справедливо и равенство x0+3·y0−1=0 , а из них по свойству транзитивности вытекает справедливость равенства (2·y0−1)+3·y0−1=0 .
Аналогично доказывается, что любое решение системы уравнений 
Суть доказательства рассматриваемого утверждения в общем виде та же. То есть, показывается, что любое решение исходной системы является решением системы, полученной после преобразования, и обратно.
Это равносильное преобразование дает разрешение на решение систем уравнений методом подстановки.
В заключение скажем, что обычно при решении систем уравнений разобранные равносильные преобразования используются сообща и иногда по нескольку раз. Дальше на практике Вы увидите это.
Алгебра. 7 класс
Конспект урока
Равносильность уравнений и систем уравнений
Перечень вопросов, рассматриваемых в теме:
- Понятие равносильных уравнений.
- Изучение равносильных систем уравнений.
- Практическое применение равносильности систем уравнений.
Уравнение, левой и правой частями которого являются числа или многочлены степени не выше первой относительно х и у, называются линейными уравнением с двумя неизвестными х и у.
Члены многочленов, находящиеся в левой и правой частях линейного уравнения, называют членами этого уравнения.
Два уравнения называют равносильными, если любое решение первого уравнения является решением второго, а любое решение второго является решением первого.
Равносильны два уравнения, каждое из которых не имеет решения.
Две системы уравнений называют равносильными, если любое решение первой системы является решением второй системы и любое решение второй системы является решением первой системы.
Равносильны две системы, если каждая из них не имеет решений.
- Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
- Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
- Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
- Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Уравнение, левой и правой частями которого являются числа или многочлены степени не выше первой относительно х и у, называются линейными уравнением с двумя неизвестными х и у.
Члены многочленов, находящиеся в левой и правой частях линейного уравнения, называют членами этого уравнения.
Два уравнения называют равносильными, если любое решение первого уравнения является решением второго, а любое решение второго является решением первого.
Равносильны такие два уравнения, каждое из которых не имеет решения.
1) Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получим уравнение, равносильное исходному.
2) Если перенести с противоположным знаком член уравнения из одной части в другую, то получим уравнение, равносильное исходному.
3) Если в левой и правой частях линейного уравнения привести подобные члены, то получится уравнение, равносильное исходному:
Доказательство этих утверждений проводится так же, как для линейного уравнения с одним неизвестным.
Две системы уравнений называют равносильными, если любое решение первой системы является решением второй системы и любое решение второй системы является решением первой системы. Равносильны также две системы, если каждая из них не имеет решений.
Очевидно, что если одно из уравнений системы заменить другим, равносильным ему уравнением, то полученная система будет равносильна исходной.
Перенеся свободные члены уравнений этой системы в их правые части, получим следующую равносильную систему:
Пример 2. Решите систему уравнений:
Решим системы способом подстановки.
Пример 3. Решите систему уравнений
Пример 4. Решите систему уравнений
Разбор решения заданий тренировочного модуля.
№1. Тип задания: единичный выбор.
Какие два уравнения называются равносильными?
Два уравнения называют равносильными, если любое решение первого уравнения является решением второго, а любое решение второго является решением первого.
Два уравнения называют равносильными, если любое решение первого уравнения не является решением второго, а любое решение второго не является решением первого.
Два уравнения называют равносильными, если любое решение первого уравнения является продолжением решения второго, и является единственно верным.
Два уравнения называют равносильными, если любое решение первого уравнения является решением второго, а любое решение второго является решением первого.
№2. Тип задания: Восстановление последовательности элементов горизонтальное / вертикальное.
Каждое уравнение системы можно записать в более компактной форме
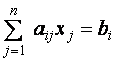
где 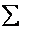
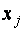
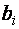
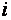
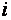
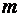
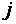
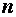
Упорядоченная совокупность 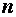

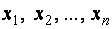
Другими словами: решением системы (1) является некоторый вектор 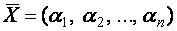
Система линейных уравнений, имеющая хотя бы одно решение, называется совместной, не имеющая ни одного решения, называется несовместной.
Совместная система линейных уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Две системы линейных уравнений с одними и теми же неизвестными называются равносильными, или эквивалентными, если каждое решение одной системы является решением другой системы, и наоборот (или если обе системы несовместны).
Элементарными преобразованиями системы (1) будем называть преобразования вида:
1. Перестановка любых двух уравнений;
2. Умножение какого-либо уравнения на число, отличное от нуля;
3. Прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на одно и то же число, отличное от нуля;
4. Отбрасывание уравнения, все коэффициенты которого и свободный член равны нулю.
Справедливо следующее утверждение.
Ø При элементарных преобразованиях система (1) переходит в равносильную ей систему.
Приведем пример решения системы линейных уравнений с помощью элементарных преобразований.
Пример 1 . Решите с помощью элементарных преобразований следующую систему линейных уравнений
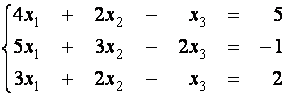
Будем использовать для обозначения эквивалентности систем уравнений знак Û .
(первое уравнение умножим на (-1) и прибавим ко второму)
(третье уравнение умножим на (-1) и прибавим к первому)
(второе уравнение умножим на (-1) и прибавим к третьему)
(первое уравнение умножим на (-1) и прибавим ко второму, а затем умножим его же на (-2) и прибавим к третьему)
(третье уравнение умножим на (-1) и прибавим ко второму)
(второе уравнение умножим на (-1) и после этого переставим с третьим)

Мы привели исходную систему к виду, разрешенному относительно неизвестных, откуда 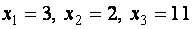
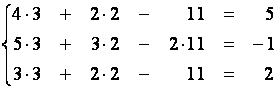

Получили три верные числовые равенства.
Итак, искомое решение 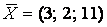
Анализируя процесс решения системы, сделаем несколько наблюдений.
1. В каждом уравнении преобразованной системы содержится ровно одна неизвестная (а остальные исключены), но четкого плана ее получения не видно.
2. Преобразованная система содержит 3 уравнения – столько же, сколько и исходная. Технически это понятно, так как использовались только три первые из элементарных преобразований, а четвертое применять не потребовалось.
3. В процессе преобразований уравнений системы фактически изменялись только ее коэффициенты и свободные члены.
Метод последовательного исключения неизвестных принадлежит великому немецкому математику Карлу Фридриху Гауссу (1777-1855) и, естественно, носит его имя.
Этот метод был усовершенствован известным французским математиком Камилем Мари Эдмоном Жорданом (1838-1922) и в новом виде стал называться методом Жордана-Гаусса .
Мы рассмотрим последовательно оба метода: метод Гаусса и метод Жордана-Гаусса .
В плане использования третьего наблюдения введем понятие матрицы.
Матрицей размера 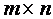
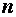
Числа, входящие в матрицу, принято называть ее элементами и обозначать 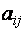
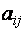
Сама матрица сокращенно обозначается символом 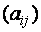
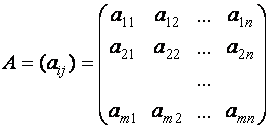
При этом 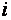
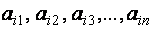
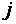
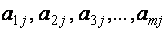
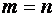
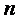
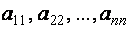
Матрица 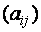
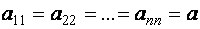
Скалярная матрица при 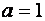
Треугольной будем называть квадратную матрицу, все элементы которой ниже (или выше) главной диагонали равны нулю.
Ступенчатой матрицей назовем матрицу, в которой каждая строка, кроме первой, начинается с нулей, причем их число возрастает с ростом номера строки, но последняя строка содержит по крайней мере один ненулевой элемент.
Примерами ступенчатой матрицы могут служить матрицы

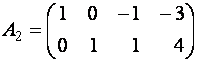
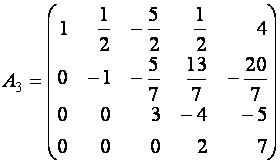

Заметим, что треугольная матрица является частным случаем ступенчатой. Примером треугольной матрицы служит матрица 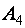
Теперь мы можем установить соответствие между системами линейных уравнений и матрицами.
Для каждой системы (1) 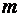
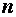
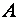
и матрицу 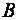
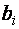
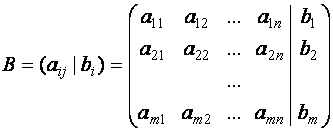
Таким образом, матрица 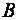
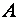
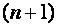
Матрицу 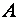
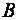
С другой стороны, имея матрицу 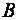
В полной аналогии с элементарными преобразованиями системы линейных уравнений введем элементарные преобразования строк матрицы:
1. Перестановка любых двух строк;
2. Умножение любой строки на число, отличное от нуля;
3. Прибавление к одной строке другой строки, умноженной на число, отличное от нуля;
4. Выбрасывание нулевой строки.
Если матрица 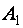
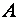
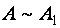
С помощью элементарных преобразований строк любую (ненулевую) матрицу можно привести к ступенчатому (в частности, треугольному) виду.
Покажем это на примере.
Пример 2 . Приведите к ступенчатому виду матрицу
Матрица 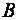
Можно было бы первую строку умножить на 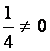
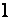
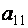
Поступим иначе: умножим третью строку на 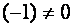
Теперь (для создания нулей в первом столбце) умножим первую строку новой матрицы на 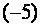
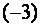
Умножим третью строку полученной матрицы на 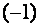
Умножим вторую строку на 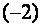
Матрица 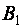
Цепочку преобразований матрицы 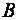
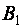



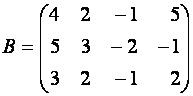

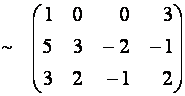


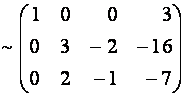



Замечание. Можно ввести понятие элементарных преобразований и для столбцов матрицы.
http://resh.edu.ru/subject/lesson/7272/conspect/
http://lms2.sseu.ru/courses/eresmat/metod/met5/parmet5_1.htm