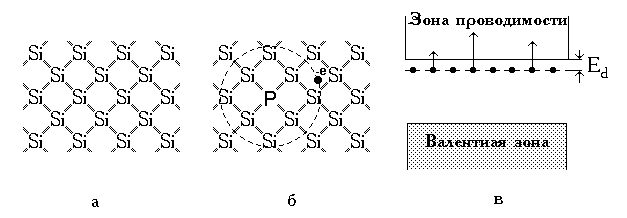
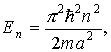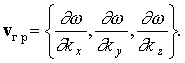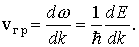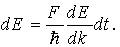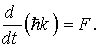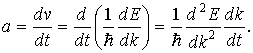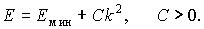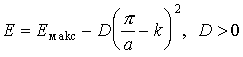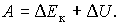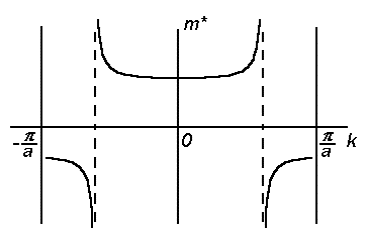ЗОННАЯ ТЕОРИЯ ТВЕРДЫХ ТЕЛ
2.1. Движение электронов в периодическом поле кристалла.
Уравнение Шредингера для кристалла
В первой главе обсуждалось квантово-механическое описание свободных микрочастиц или частиц, находящихся во внешнем силовом поле. Однако основные успехи квантовой механики связаны с изучением систем взаимодействующих микрочастиц (электронов, ядер, атомов, молекул), из которых состоит вещество. В этой главе мы применим квантовую механику к описанию поведения электронов в твердых кристаллических телах, рассматривая кристалл как систему микрочастиц.
В общем случае эта задача требует решения уравнения Шредингера для системы частиц (электронов и ядер), образующих кристалл. В этом уравнении необходимо учесть кинетическую энергию всех электронов и ядер, потенциальную энергию взаимодействия электронов между собой, ядер между собой, электронов с ядрами. Понятно, что в общем виде решение такого уравнения не представляется возможным, поскольку оно содержит порядка 10 22 переменных. Поэтому задачи, связанные с поведением электронов в кристалле, решаются при некоторых упрощающих допущениях (приближениях), правомерность которых определяется конкретными свойствами кристалла. Рассмотрим основные из этих допущений.
Адиабатическое приближение. В этом приближении предполагается, что электроны движутся в поле неподвижных ядер. Под ядрами здесь подразумевают собственно ядра атомов со всеми электронам, исключая валентные. Правомерность этого допущения определяется тем, что скорости электронов приблизительно на два порядка больше, чем скорости ядер, поэтому для любой, даже неравновесной конфигурации ядер всегда будет успевать устанавливаться соответствующее ей электронное равновесие. В этом представлении исключается обмен энергией между электронной и ядерной системами, поэтому это приближение называется адиабатическим. Естественно, что в адиабатическом приближении нельзя рассматривать такие явления, как диффузия, ионная проводимость и др., связанные с движением атомов или ионов.
Одноэлектронное приближение. В этом приближении вместо взаимодействия данного электрона с остальными электронами и ядрами по отдельности рассматривают его движение в некотором результирующем усредненном поле остальных электронов и ядер. Такое поле называют самосогласованным. В одноэлектронном приближении, таким образом, задача сводится к независимому описанию каждого электрона в среднем внешнем поле с потенциальной энергией U(r). Вид функции U(r) определяется свойствами симметрии кристалла. Основное свойство самосогласованного поля заключается в том, что оно имеет тот же период, что и поле ядер.
Таким образом, адиабатическое и одноэлектронное приближение приводит к задаче движения электрона в некотором периодическом потенциальном поле, имеющем период, равный постоянной решетки кристалла. Уравнение Шредингера в этом случае будет иметь вид
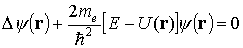
Следующие два допущения связаны с невозможностью точно определить вид функции U(r). Поэтому обычно при описании свойств электронов в кристалле рассматривают два предельных случая взаимодействия электронов с решеткой.
Приближение слабой связи. В этом приближении электроны в кристалле рассматривают как почти свободные частицы, на движение которых оказывает слабое возмущение поле кристаллической решетки. Данное допущение применимо, когда потенциальная энергия взаимодействия электрона с решеткой много меньше его кинетической энергии. Такой подход, который иногда называют «приближением почти свободных электронов«, позволяет получить решение некоторых задач, связанных с поведением валентных электронов в металлах.
В полупроводниках более приемлемым для анализа их физических свойств является приближение сильной связи. В этом приближении состояние электрона в кристалле мало отличается от его состояния в изолированном атоме. Приближение сильной связи применимо, когда потенциальная энергия электрона значительно больше его кинетической энергии.
Характерным для обоих приближений слабой и сильной связи является то, что оба они приводят к фундаментальному свойству энергетического распределения электронов в кристалле — возникновению разрешенных и запрещенных энергетических зон.
2.2. Энергетические зоны в приближении сильной связи
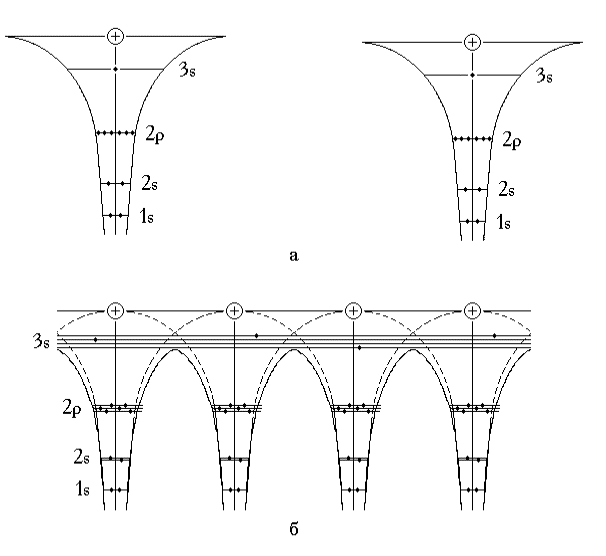
Несмотря на то, что метод сильной связи применим для электронов глубоких энергетических уровней, он хорошо иллюстрирует общие закономерности образования энергетических зон при сближении изолированных атомов и образования из них кристаллической решетки. Рассмотрим качественно картину возникновения энергетических зон на примере образования кристаллической решетки из изолированных атомов натрия. Электронная структура Na 11 (1s 2 2s 2 2p 6 3s): всего в атоме 11 электронов, по два электрона на 1s и 2s уровнях, 6 электронов на уровне 2р, последний заполненный уровень в атоме натрия — 3s, на котором находится один валентный электрон. Поскольку в приближении сильной связи предполагается, что состояние электрона в кристалле незначительно отличается от его состояния в изолированном атоме, будем в оценке влияния на это состояние кристаллического поля соседних атомов исходить из энергетической структуры изолированного атома. На рис. 2.1,а показаны схематически энергетические уровни и распределение электронов на них для атомов натрия, находящихся на достаточно большом расстоянии друг от друга так, что потенциальные кривые электронов не перекрываются (взаимодействие между атомами пренебрежимо мало). Состояния электронов в этом случае описываются волновыми функциями изолированного атома, разрешенные уровни энергии дискретны и определяются квантовыми числами n, l, m — главным, орбитальным, магнитным соответственно. На каждом невырожденном по энергии уровне могут находиться с учетом спина по два электрона, а на каждом вырожденном по орбитальному квантовому числу уровне 2(2l +1) электронов.
Рис. 2.1. Изменение состояния электронов при сближении атомов
Сблизим теперь эти атомы на расстояние, равное параметру кристаллической решетки натрия (рис. 2.1,б). Взаимодействие с соседними атомами будет оказывать влияние на первоначальные атомные энергетические уровни. В приближении сильной связи предполагается, что потенциальная энергия электрона в кристалле U(r) может быть представлена суммой
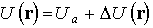
где Ua — потенциальная энергия электрона в изолированном атоме; D U (r) — поправка, учитывающая влияние соседних атомов. Предполагается, что соседние атомы оказывают слабое возмущение на Ua( D U (r) D U (r) приводит к уравнению Шредингера для изолированного атома.
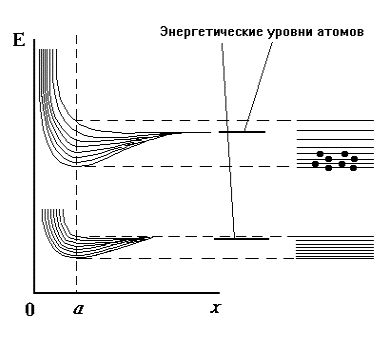
Поскольку в кристалле каждый уровень изолированного атома повторяется N раз, то он становится N-кратно вырожденным. Известно, что электрическое поле снимает вырождение и каждый уровень изолированного атома расщепляется на N близко расположенных (по значениям энергии) энергетических уровней. Здесь имеется аналогия со связанными осцилляторами. Если мы имеем два не связанных между собой каким-либо взаимодействием совершенно одинаковых осциллятора (математические маятники, электрические колебательные контуры и др.), то частоты их собственных колебаний совпадают. Взаимодействие между осцилляторами приводит к расщеплению одной частоты на две близкие частоты (при условии, что энергия взаимодействия между осцилляторами много меньше энергии собственных колебаний). Для N связанных между собой осцилляторов получим полосу из N близко расположенных частот. Аналогичный результат получается для системы взаимодействующих атомов. Число энергетических уровней, на которые расщепляется каждый энергетический уровень изолированного атома, равно числу атомов в кристалле. Величина расщепления тем больше, чем сильнее взаимодействие между атомами, т.е. чем меньше расстояние между ними. На рис. 2.2 показано схематически расщепление двух энергетических уровней атома под воздействием полей соседних атомов. Схема приведена для восьми атомов.
Решение уравнения Шредингера в приближении сильной связи приводит к следующему выражению для энергии электрона в периодическом поле трехмерной кубической решетки
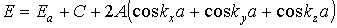
здесь C — некоторая постоянная величина, которая может принимать положительные и отрицательные значения; А — обменный интеграл, зависящий от перекрытия волновых функций атомов; k x , k y , k z — компоненты волнового вектора электрона; а — параметр решетки кристалла.
Рис.2.2. Расщепление энергетических уровней атома
Экстремальные значения энергии электрона Е имеют место при coskia = ± 1 (i = x, y, z) и определяют ширину энергетической зоны, образованной расщепленным уровнем изолированного атома. Для простой кубической решетки ширина энергетической зоны D E = 12A . Ширина энергетической зоны для более высоких уровней больше, т.к. для этих состояний электронов сильнее перекрываются волновые функции электронов и, следовательно, больше обменный интеграл А. Середина зоны сдвинута относительно положения энергетического уровня изолированного атома на величину С. Направление смещения зависит от знака С. Энергетические зоны в общем случае разделены интервалами энергии D E g , называемыми запрещенными зонами. Иногда энергетические зоны могут перекрываться.
В реальных кристаллах размером приблизительно 1 см 3 содержится
10 22 атомов. Ширина энергетической зоны обычно
1 эВ. В этом случае расстояние между уровнями в зоне составляет
10 -22 эВ. Следовательно, спектр электронов в пределах энергетической зоны можно считать практически непрерывным.
2.3. Общие свойства волновой функции электрона в периодическом потенциале. Теорема Блоха
Для точного решения в одноэлектронном приближении задачи о движении электрона в кристалле необходимо решить уравнение Шредингера вида (2.1), где потенциал U(r) имеет периодичность кристаллической решетки, т.е.
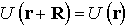
здесь R — любой вектор прямой кристаллической решетки.
Необходимость решения квантово-механической задачи связана с тем, что длина волны де Бройля электрона по порядку величины совпадает с периодом потенциала U (
10 -8 cм). Можно получить некоторые общие свойства волновой функции электрона в кристалле, используя только свойство периодичности потенциала кристаллического поля, не решая уравнения Шредингера. Мы будем рассматривать здесь идеализированный случай гипотетического кристалла с абсолютно идеальной периодичностью потенциала. Типичный вид потенциала вдоль линии, соединяющей цепочку атомов (одномерный случай) мы получили ранее, анализируя качественно влияние взаимодействия атомов на спектр электронов при сближении изолированных атомов (рис. 2.1,б). Точное определение функции U(r) является очень сложной задачей.
Фундаментальные свойства волновой функции стационарного состояния определяются теоремой Блоха: собственные функции стационарного волнового уравнения с периодическим потенциалом имеют вид произведения функции плоской волны на функцию с периодичностью потенциала:
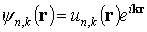
Индекс k у волновой функции указывает на то, что эта функция зависит от волнового числа. Появление индекса n связано с тем, что при фиксированных значениях k волновая функция не одинакова для электронов различных зон, образовавшихся из атомных уровней, n часто называют номером зоны. Множитель un,k(r) называют блоховским множителем. Он учитывает влияние кристаллического поля и отражает тот факт, что вероятность нахождения электрона в той или иной области кристалла повторяется от ячейки к ячейке.
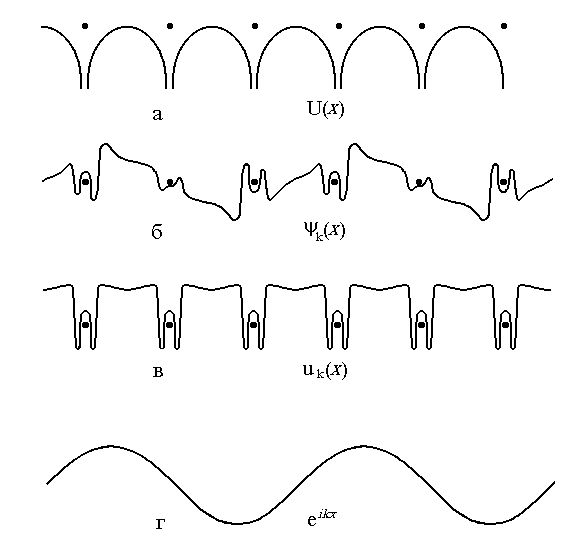
Схематическое изображение электронных волновых функций, представленных в теореме Блоха, показано для одномерного случая на рис.2.3. Вверху (рис. 2.3,а) представлен потенциал U(x) вдоль цепочки атомов. Ниже (рис. 2.3,б) приведен пример собственной функции (ее действительной части). Эта функция равна произведению блоховского множителя u(x), имеющего периодичность решетки (рис. 2.3,в) и волновой функции свободного электрона в виде плоской волны (рис. 2.3,г), длина которой определяется волновым числом k. Представление волновой функции в виде (2.4) может быть сделано различными способами. Покажем это для одномерного случая. Одномерная волновая функция по теореме Блоха может быть записана в виде
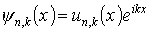
Домножим и разделим правую часть равенства (2.5) на функцию 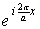
а — параметр решетки. Тогда получим
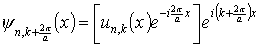
Рис. 2.3. Схематическое изображение электронных волновых функций в кристалле
В квадратных скобках формулы (2.6) стоит функция, удовлетворяющая требованиям теоремы Блоха: она является периодической с периодом а, т.к. равна произведению двух периодических функций с тем же периодом. Функция 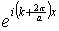
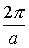
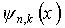
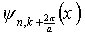
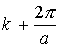
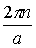
Для одномерной цепочки атомов величина 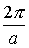
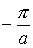
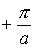
2.4. Модель Кронига-Пенни
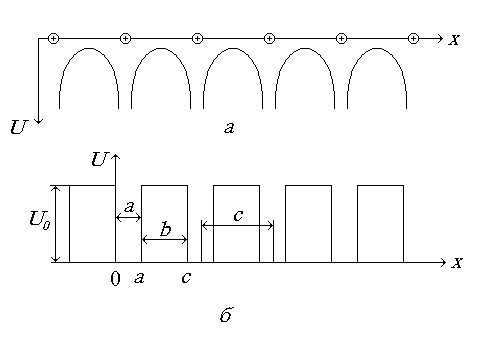
Теорема Блоха позволяет аналитически решить задачу об электроне в периодическом поле кристаллической решетки в приближении слабой связи при некоторых упрощающих предположениях. Основная трудность в решении уравнения (2.1) связана с невозможностью точно записать вид функции U(r). Поэтому часто периодическую зависимость функции U(r) заменяют более простой функцией с точно таким же периодом. В модели Кронига-Пенни ограничиваются рассмотрением одномерной задачи, в которой периодический потенциал заменяется цепочкой прямоугольных потенциальных ям (рис. 2.4). Ширина каждой ямы а, они отделены друг от друга прямоугольными потенциальными барьерами высотой U 0 и шириной b. Период повторения ям с = а + b.
Рис.2.4. Изменение потенциальной энергии электрона:
а — в реальном кристалле; б — в модели Кронига-Пенни
Стационарное уравнение Шредингера будет иметь в этом случае вид
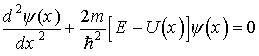
Начало системы координат (точку х = 0) выберем так, чтобы она совпадала с левым краем потенциальной ямы, как это показано на рис. 2.4,б. Tогда потенциальная функция
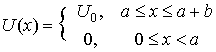
В соответствии с теоремой Блоха волновая функция электрона y (x) может быть представлена в виде
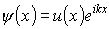
Индексы n и k упущены для простоты записи. Функция u(x) (блоховский множитель) имеет период c
Подставляя (2.9) в уравнение (2.7), получим дифференциальное уравнение для блоховского множителя
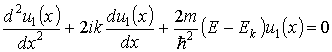
для электронов, находящихся внутри потенциальных ям, и
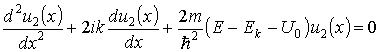
для электронов, находящихся вне потенциальных ям. В этих уравнениях Ek — кинетическая энергия электрона
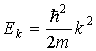
Общее решение уравнения (2.10а) для электронов внутри потенциальных ям может быть записано в виде
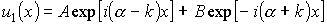
где a — некоторый параметр, который может быть найден подстановкой решения в виде (2.11а) в исходное уравнение (2.10а). Эта подстановка приводит к следующему значению a :
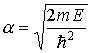
В области вне потенциальных ям при условии, что высота потенциального барьера U0 выше полной энергии электрона Е, решение уравнения (2.10б) имеет вид
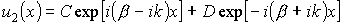
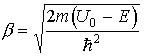
Постоянные A, B, C и D в формулах (2.11а) и (2.11б) находятся как обычно из граничных условий. Граничные условия требуют, чтобы функция u(x) и ее первая производная в местах скачков потенциала, т. е. на стенках потенциальных ям, были непрерывны. Эти требования приводят к следующей системе уравнений:
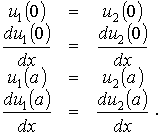
Система уравнений (2.12) после подстановки в нее функций 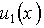
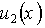
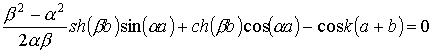
Выражение (2.13) можно значительно упростить, если допустить, что ширина барьера стремится к нулю 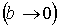
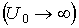
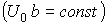

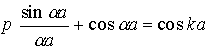
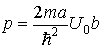
Поскольку a — параметр, определяемый энергией Е электрона, а k — волновой вектор электрона, то выражение (2.14) представляет зависимость E(k), т. е. дисперсионное соотношение для электрона в кристаллической решетке. Это дисперсионное соотношение можно записать в явном виде, решив уравнение (2.14) относительно a при фиксированном значении параметра p.
2.5. Энергетические зоны в модели Кронига-Пенни
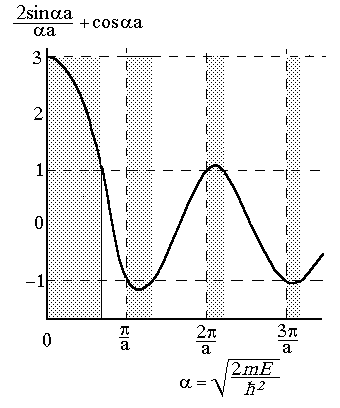
Найдем в явном виде дисперсионное соотношение для электрона в периодическом кристаллическом поле. Исследуя выражение (2.14) находим, что волновое число k может быть вещественным только при условии, что значения левой части этого равенства находятся в интервале от -1 до +1. Зависимость левой части уравнения (2.14) от a для параметра p = 2 приведен на рис. 2.5. Заштрихованные участки соответствуют запрещенным значениям параметра a и, следовательно, энергии электрона в кристалле. Этот результат получен только на основании теоремы Блоха, условием применимости которой является единственное требование периодичности потенциала в стационарном уравнении Шредингера для электрона в кристалле. Таким образом, наличие периодического потенциала приводит к появлению для энергии электрона таких интервалов, для которых нет волнового решения, соответствующего вещественным значениям волнового числа электрона. Результатом этого является чередование разрешенных и запрещенных зон энергии для электрона в кристалле.
Рис. 2.5. Зависимость от параметра a левой части уравнения (2.14)
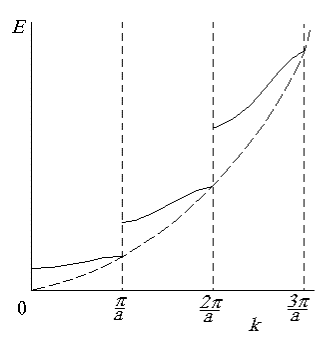
Рис. 2.6. Зависимость энергии электрона от волнового числа для p =2 и p =0 (штриховая линия)
На рис. 2.6 приведено дисперсионное соотношение для энергии электрона в кристалле. Видно, что зависимость E(k) претерпевает разрывы в точках, где 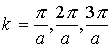
Если параметр p = 0, согласно равенству (2.14) 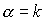
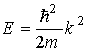
Последнее равенство соответствует дисперсионному соотношению для свободного электрона. На рис. 2.6 это дисперсионное соотношение изображено штриховой линией.
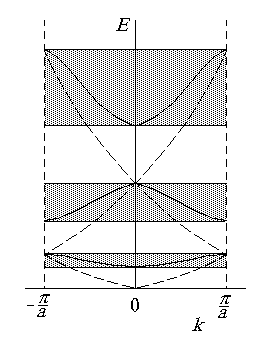
Поскольку, как подчеркивалось выше, все физически различимые значения волнового числа лежат в пределах первой зоны Бриллюэна, которая в одномерном случае ограничена интервалом значений волнового числа от 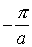
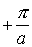
Рис.2.7. Энергия электрона как функция волнового числа в схеме приведенных зон Бриллюэна
Предел P ® ¥ дает дискретный ряд уровней
которые совпадают с полученными в первой главе результатами для частицы в одномерной прямоугольной потенциальной яме (см. уравнение (1.34)). Энергия электронов в периодическом поле кристалла претерпевает разрыв на границах зон Бриллюэна, для которых 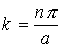
отражением электронных волн от атомных плоскостей кристаллической решетки. Действительно, с учетом того, что 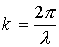
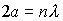
2.6. Заполнение энергетических зон электронами.
Металлы, диэлектрики и полупроводники
Твердые тела делятся на металлы, диэлектрики и полупроводники прежде всего по величине удельной электропроводности. Для типичных металлов эта величина составляет 10 8 . 10 6 (Ом • м) -1 . В диэлектриках удельная электропроводность ничтожно мала: s -8 (Ом • м) -1 . Для хороших диэлектриков удельная электропроводность достигает величины 10 -11 (Ом • м) -1 . Твердые тела с промежуточной электропроводностью относят к полупроводникам. Оказывается, что столь большие различия в электрических свойствах твердых тел связаны со структурой и степенью заполнения электронами энергетических зон в этих телах.
Несмотря на то, что энергетические зоны квазинепрерывны, они состоят пусть из очень большого, но конечного числа энергетических уровней. Число этих уровней определяется числом атомов N, объединенных в кристалл, и орбитальным квантовым числом l:
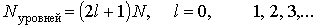
В каждой энергетической зоне могут располагаться в соответствии принципом Паули не более 2(2l + 1) электронов — по два с противоположными спинами на каждом уровне. Число электронов в кристалле также конечно и зависит как от числа атомов N, так и от количества электронов в атоме. Поскольку электроны стремятся занять энергетические уровни с наинизшей энергией, то в кристалле нижние энергетические зоны оказываются полностью заполненными, а самые верхние заполнены либо частично, либо совершенно свободны.
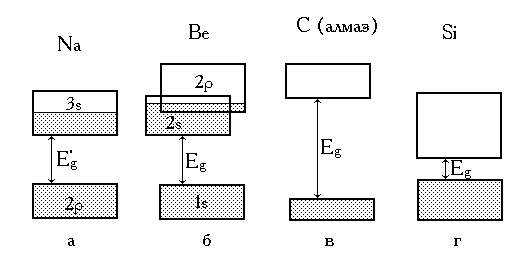
Частично заполненная зона образуется, например, у кристалла натрия. Этот элемент имеет полностью заполненные 1s-, 2s- и 2p-уровни, на которых располагается в общей сложности 10 электронов. В кристалле Na соответствующие 1s-, 2s- и 2p-зоны также будут полностью заполнены. Одиннадцатый валентный электрон в атоме Na располагается на 3s-уровне, на котором могут располагаться 2 электрона. Следовательно, 3s-зона кристаллического натрия будет заполнена лишь наполовину. Зонная структура Na приведена на рис. 2.8,a. Заполненные электронами зоны и часть 3s-зоны заштрихованы. Eg — ширина запрещенной зоны.
Часто частично заполненная зона образуется в результате перекрытия полностью заполненной зоны со следующей совершенно свободной. Пример такой зонной структуры приведен на рис. 2.8,б для бериллия, у которого перекрываются заполненная 2s- и свободная 2p-зоны.
Большую группу составляют кристаллы, у которых над целиком заполненным зонами располагаются совершенно пустые зоны, причем ширина запрещенной зоны варьируется у них от нескольких десятков электронвольт до единиц электронвольт. Типичные примеры этой группы кристаллов показаны на рис. 2.8, в, г. Это углерод в модификации алмаза и кремний.
Структура энергетических зон кристалла оказывает решающее влияние на величину его электропроводности. Поскольку электрический ток есть направленное движение зарядов (в металлах — электронов), то возникновение электрического тока связано с увеличением импульса электронов вдоль направления действующей на него силы. Вместе с импульсом электрона меняется его волновой вектор. Поскольку энергия и волновой вектор электрона — две взаимосвязанные величины, связь между которыми определяется дисперсионным соотношением, то увеличение волнового числа должно обязательно сопровождаться увеличением энергии электрона. Нетрудно оценить, каково увеличение энергии электрона за счет его ускорения в электрическом поле, вызывающим электрический ток в проводниках. Если величина напряженности электрического поля равна 10 4 В/м, то на расстоянии, равном средней длине свободного пробега электрона в кристалле, а она обычно составляет
10 -8 м, электрон приобретает энергию приблизительно 10 -4 эВ. Понятно, что эти значения энергии позволяют электрону переходить с уровня на уровень только внутри одной энергетической зоны. Для перехода между зонами необходима энергия больше ширины запрещенной зоны Eg, которая, как указывалось выше, составляет 0.1 . 10 эВ.
Рис.2.8. Заполнение энергетических зон электронами
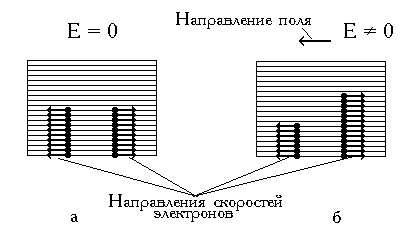
Эти рассуждения приводят к выводу о том, что для появления у тел высокой проводимости необходимо, чтобы в их энергетическом спектре присутствовали зоны, заполненные частично. На свободные уровни этих зон могут переходить электроны, увеличившие свою энергию под действием внешнего электрического поля (рис. 2.9). Поэтому тела с частично заполненными энергетическими зонами являются проводниками. Частично заполненные зоны имеют все металлы.
 |
Теперь рассмотрим кристаллы, верхняя энергетическая зона которых заполнена электронами полностью (рис. 2.8, в, г). Внешнее электрическое поле не в состоянии изменить характер движения электронов, т. к. оно не в состоянии поднять электроны в вышележащую свободную зону. Внутри же самой полностью заполненной зоны, не содержащей ни одного свободного уровня, оно может вызывать лишь перестановку электронов местами, что не нарушает симметрии их распределения по скоростям. Это не приводит к возникновению электрического тока в таких кристаллах.
Таким образом, твердые тела с полностью заполненными электронами энергетическими зонами являются непроводниками. По ширине запрещенной зоны непроводники делятся на диэлектрики и полупроводники.
К диэлектрикам относят тела, имеющие относительно широкую запрещенную зону. У типичных диэлектриков Eg > 3 эВ. Так, у алмаза Eg = 5,2 эВ; у нитрида бора Eg = 4,6 эВ; у Al2O3 Eg = 7 эВ.
У типичных полупроводников ширина запрещенной зоны менее 3 эВ. Например, у германия Eg = 0,66 эВ; у кремния Eg = 1,12 эВ; у антимонида индия Eg = 0,17 эВ.
Верхняя заполненная зона полупроводников и диэлектриков называется валентной зоной, следующая за ней свободная зона называется зоной проводимости. В металлах частично заполненную зону называют как валентной зоной, так и зоной проводимости.
2.7. Эффективная масса электрона в кристалле и ее физический смысл
Особенности движения электронов в кристалле обусловлены их взаимодействием с кристаллической решеткой. Оказывается, что движение отдельного электрона в кристалле можно описывать тем же уравнением, что и для свободной частицы, т.е. в виде второго закона Ньютона, в котором учитываются только внешние по отношению к кристаллу силы.
Рассмотрим движение электрона в кристалле под действием внешнего электрического поля. Внешнее электрическое поле приводит к увеличению скорости электрона и, следовательно, его энергии. Поскольку электрон в кристалле — это микрочастица, описываемая волновой функцией, то энергия электрона зависит от его волнового вектора. Зависимость между этими двумя характеристиками электрона в кристалле определяется дисперсионным соотношением, которое в свою очередь зависит от строения энергетических зон. Поэтому при расчете движения электрона в кристалле необходимо исходить из закона дисперсии.
Свободный электрон описывается монохроматической волной де Бройля и электрон в этом состоянии нигде не локализован. В кристалле же электрону необходимо сопоставить группу волн де Бройля с различными значениями частот w и волновых векторов k. Центр такой группы волн перемещается в пространстве с групповой скоростью
Эта групповая скорость соответствует скорости перемещения электрона в кристалле.
Задачу о движении электрона будем решать для одномерного случая. Увеличение энергии электрона dE под действием внешней силы F равно элементарной работе dA, которую совершает внешняя сила за бесконечно малый промежуток времени dt:
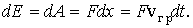
Учитывая, что для электрона как микрочастицы 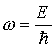
Подставляя полученное выражение для групповой скорости в формулу (2.16), получим
Распространяя этот результат на трехмерный случай, получим векторное равенство
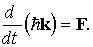
Как видно из этого равенства, величина ћ k для электрона в кристалле изменяется со временем под действием внешней силы точно так же, как импульс частицы в классической механике 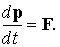
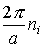
Вычислим теперь ускорение a, приобретаемое электроном под действием внешней силы F. Ограничимся, как и в предыдущем случае, одномерной задачей. Тогда
При вычислении ускорения учтено, что энергия электрона является функцией времени 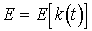
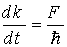
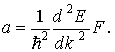
Сравнивая выражение (2.18) со вторым законом Ньютона, видим, что электрон
в кристалле движется под действием внешней силы так, как двигался бы под действием той же силы свободный электрон, если бы он обладал массой
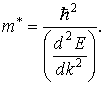
Величину m* называют эффективной массой электрона в кристалле.
Строго говоря, эффективная масса электрона никакого отношения к массе свободного электрона не имеет. Она является характеристикой системы электронов в кристалле в целом. Вводя понятие эффективной массы, мы реальному электрону в кристалле, связанному взаимодействиями с кристаллической решеткой и другими электронами, сопоставили некую новую свободную “микрочастицу”, обладающую лишь двумя физическими параметрами реального электрона — его зарядом и спином. Все остальные параметры — квазиимпульс, эффективная масса, кинетическая энергия и т.д. — определяются свойствами кристаллической решетки. Такую частицу часто называют квазиэлектроном, электроном-квазичастицей, носителем отрицательного заряда или носителем заряда n-типа, чтобы подчеркнуть ее отличие от реального электрона.
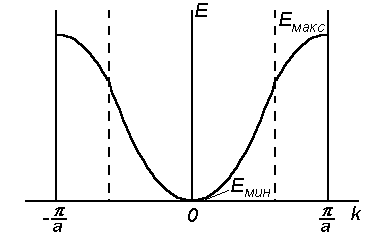
Особенности эффективной массы электрона связаны с видом дисперсионного соотношения электрона в кристалле (рис.2.10). Для электронов, располагающихся у дна энергетической зоны, дисперсионное соотношение можно приблизительно описать параболическим законом
Вторая производная 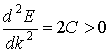
Для электронов, находящихся у вершины энергетической зоны (рис.2.10), дисперсионное соотношение можно приблизительно описать параболой вида
и эффективная масса является величиной отрицательной. Такое поведение эффективной массы электрона объясняется тем, что он при своем движении в кристалле обладает не только кинетической энергией поступательного движения Ек, но и потенциальной энергией его взаимодействия с кристаллической решеткой U. Поэтому часть работы A внешней силы может перейти в кинетическую энергию и изменить ее на величину D Eк , другая часть — в потенциальную D U :
Рис. 2.10. Закон дисперсии для электрона в кристалле
Рис. 2.11. Зависимость эффективной массы электрона от волнового числа
Если при движении электрона в потенциальную энергию переходит не только вся работа внешней силы, но и часть кинетической энергии, имевшейся у электрона ( D Eк 0 ), то его скорость будет уменьшаться. В этом случае электрон ведет себя как частица с отрицательной эффективной массой. В случае, когда вся работа внешней силы переходит в потенциальную энергию ( D Eк = 0 ), то приращения кинетической энергии и скорости не происходит. Электрон ведет себя как частица с бесконечно большой эффективной массой. Бесконечно большой эффективной массой обладает электрон в точках перегиба дисперсионной кривой, которые на рис. 2.10 обозначены штриховыми линиями. Схематически зависимость эффективной массы электрона от его волнового числа показана на рис. 2.11.
2.8. Собственные полупроводники. Понятие о дырках
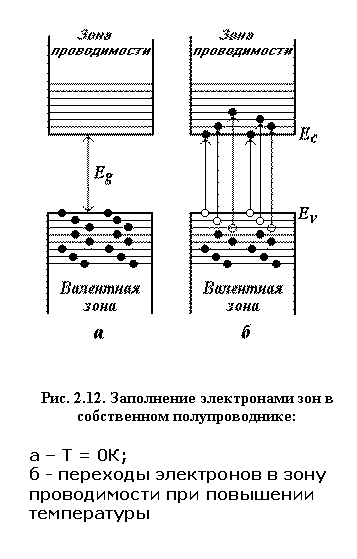
Из структуры энергетических зон полупроводников следует, что при абсолютном нуле они не проводят электрического тока. Нагревание их приводит к тому, что часть электронов валентной зоны приобретает энергию, достаточную для их перехода в зону проводимости, в результате чего появляется заметная электропроводность. С увеличением температуры число электронов в зоне проводимости увеличивается и вместе с этим растет электропроводность полупроводника. Тепловое возбуждение электронов проводимости иллюстрирует рис. 2.12. Ес и Еv обозначают дно зоны проводимости и потолок валентной зоны соответственно. Кроме температуры, возбуждение электронов проводимости может происходить и под действием других факторов, способных сообщить электронам энергию, достаточную для перехода их в зону проводимости. Этими факторами могут быть световое облучение, ионизирующее излучение и др.
 |
Рассмотренный выше механизм возникновения электропроводности полупроводниковых кристаллов, справедлив для абсолютно чистых материалов, не содержащих примесей, влияющих на электропроводность. Такие полупроводники называются собственными, а их электропроводность собственной электропроводностью. К собственным полупроводникам относятся кристаллы чистых химических элементов, таких как германий (Ge), кремний (Si), селен (Se), теллур (Te) и др., а также некоторые химические соединения: арсенид галлия (GaAs), арсенид индия (InAs), антимонид индия (InSb), карбид кремния (SiC) и многие другие.
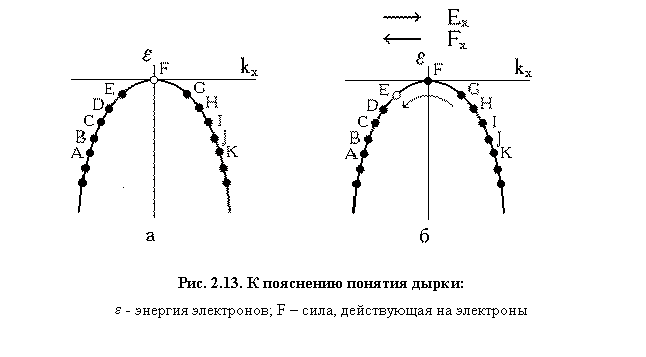 |
В разделе 2.8 показано, что электроны, расположенные у по-толка энергетической зоны, об-ладают отрицательной эффектив-ной массой. Именно такие электроны, расположенные у вершины валентной зоны, переходят в зону проводимости и участвуют в электропроводности полупроводника. Каждому электрону, перешедшему в зону проводимости, в валентной зоне соответствует незанятое (вакантное) состояние, которое называют дырочным состоянием. Дырочные состояния изображены на рис. 2.12 светлыми кружками. Наличие вакансий в валентной зоне позволяет электронам этой зоны изменять свое энергетическое состояние под действием внешнего электрического поля. Рассмотрим подробнее этот процесс на примере кристалла, в котором имеется одно вакантное состояние. В отсутствие электрического поля это состояние будет находиться в вершине зоны, т.к. электроны стремятся расположиться на уровнях с наименьшей энергией (рис. 2.13,а). Занятые электронами состояния изображены на рис. 2.13 точками и расположены на дисперсионной кривой, описывающей зависимость энергии электрона от компоненты волнового вектора k x . У вершины энергетической зоны эта кривая приблизительно описывается параболой. Если к полупроводнику приложить внешнее электрическое поле Е (пусть для определенности оно будет направлено вдоль положительного направления оси х, рис. 2.13,б) , то у каждого электрона х-компонента волнового вектора kx одновременно получит отрицательное приращение. Этот вывод следует из уравнения движения, одинакового для каждого электрона:
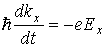
Следовательно, электроны валентной зоны будут перемещаться в направлении, указанном стрелкой на рис. 2.13,б. Вакантное состояние в результате этого движения электронов вначале переместится в точку Е, а затем — в точку D и т.д. Таким образом, последовательное перемещение электронов по энергетическим уровням под влиянием электрического поля эквивалентно перемещению вакантного состояния. Квантовое состояние, не занятое электроном в энергетической зоне, называется дыркой. Суммарный волновой вектор электронов в полностью заполненной энергетической зоне равен нулю, поскольку дисперсионная кривая симметрична относительно точки k = 0 и каждому электрону с волновым вектором k всегда найдется электрон с противоположным по знаку волновым вектором — k . Если из состояния с волновым вектором ke удален электрон, то полный волновой вектор системы станет равным — k e . Таким образом, дырке следует приписать волновой вектор
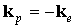
Учитывая (2.20) и (2.21), уравнение движения дырки будет иметь вид
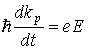
Это уравнение движения положительного заряда в электрическом поле. Поскольку дырка перемещается вдоль направления действующей на нее силы, то этой частице следует приписать положительную эффективную массу, равную по абсолютному значению отрицательной эффективной массе электрона, покинувшего вакантное состояние у потолка валентной зоны.
Вычислим ток, создаваемый электронами полностью заполненной энергетической зоны. Вклад в плотность тока от одного электрона, движущегося со скоростью vj равен
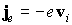
Ток всех электронов валентной зоны равен сумме токов отдельных электронов:
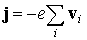
Суммирование производится по всем состояниям, занятым электронами. Поскольку дисперсионные кривые симметричны, каждому электрону с ненулевым значением скорости в положительном направлении всегда найдется электрон с равной по абсолютному значению, но противоположно направленной скоростью. Следовательно, сила тока, создаваемого электронами полностью заполненной зоны, будет равна нулю.
Если в валентной зоне заняты все состояния, кроме одного, характеризующегося волновым вектором ks и скоростью vs (рис. 2.13,г), то суммарную плотность тока в этом случае можно представить в следующем виде:
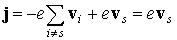
В этой формуле учтено, что первое слагаемое в силу симметричности состояний электронов равно нулю.
Таким образом, движение электронов валентной зоны, в которой есть одно вакантное состояние, эквивалентно движению одной частицы с положительной эффективной массой и положительным электрическим зарядом, помещенной в это состояние.
2.9. Примесные полупроводники
В реальных кристаллах полупроводников всегда присутствуют, пусть и в небольших количествах, дефекты, примеси, некоторые из которых оказывают существенное влияние на их электропроводность. Например, добавление в кремний бора в количестве одного атома на 10 5 атомов кремния увеличивает его электропроводность при комнатной температуре в 1000 раз. Полупроводники, содержащие примеси, существенно влияющие на его электропроводность, называются примесными полупроводниками, а их электропроводность — примесной электропроводностью.
Рассмотрим механизм примесной проводимости на примере полупроводникового кристалла кремния с примесными атомами фосфора. Четыре валентных электрона кремния образуют в химически чистом кристалле парные ковалентные связи с четырьмя своими ближайшими соседями (рис. 2.14,а). Примесный атом фосфора замещает один из атомов кремния в узле кристаллической решетки. У атома фосфора пять валентных электронов, четыре из которых поддерживают связи с соседними атомами кремния, а пятый остается свободным (рис. 2.14,б). Этот избыточный электрон может перейти в зону проводимости кремния и «участвовать» в создании электрического тока. Примеси, поставляющие в зону проводимости дополнительное количество электронов, называются донорными примесями, а полупроводники с такими примесями — донорными полупроводниками или полупроводниками n-типа. Наиболее распространенными донорными примесями в кристаллах кремния и германия являются атомы пятой группы периодической системы элементов Д. И. Менделеева: фосфор (P), мышьяк (As), сурьма (Sb), висмут (Bi). Энергию, которую необходимо затратить, чтобы перевести электрон примесного донорного атома в зону проводимости, называют энергией связи донорной примеси. Оценить энергию связи донорной примеси можно из простой модели, подобной боровской модели атома водорода. Согласно этой модели примесный электрон движется по круговой орбите в кулоновском поле сил иона фосфора подобно электрону в поле ядра атома водорода. Различие заключается в том, что поле примесного иона ослаблено диэлектрическими свойствами кристалла полупроводника. Это влияние учитывается диэлектрической проницаемостью среды, которая для типичных полупроводников составляет 5 . 2000. Необходимо учесть также тот факт, что эффективная масса электрона в кристалле отличается от массы свободного электрона. Для количественных оценок воспользуемся результатами, полученными в теории Бора для атома водорода. Энергия связи электрона в атоме водорода равна 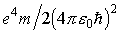
Рис. 2.14 Схема проводимости в донорном полупроводнике:
а — ковалентные связи в чистом полупроводнике кремния; б — примесный атом фосфора;
в — зонная структура донорного полупроводника
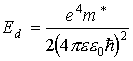
Энергия ионизации свободного атома водорода равна 13,6 эВ. В соответствии с формулой (2.23) это значение надо умножить на коэффициент 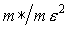
Экспериментальное значение энергии ионизации фосфора в кремнии составляет 0,044 эВ. Другие донорные примеси имеют в кремнии и германии энергию ионизации того же порядка величины (см. таблицу).
Лекция 15. Электроны в кристаллах
Лекция 15. Электроны в кристаллах
15.1. Электропроводность металлов
Квантовомеханический расчет показывает, что в случае идеальной кристаллической решетки электроны проводимости не испытывали бы при своем движении никакого сопротивления и электропроводность металлов была бы бесконечно большой. Согласно корпускулярно-волновому дуализму, движению электрона сопоставляют волновой процесс. Идеальная кристаллическая решетка металла (в ее узлах находятся неподвижные частицы и в ней отсутствуют нарушения периодичности) ведет себя подобно оптически однородной среде — она «электронные волны» не рассеивает. Это соответствует тому, что металл не оказывает электрическому току — упорядоченному движению электронов — никакого сопротивления. «Электронные волны», распространяясь в идеальной кристаллической решетке металла, как бы огибают узлы решетки и проходят значительные расстояния.
В реальной кристаллической решетке металла всегда имеются неоднородности, которыми могут быть, например, примеси, вакансии; неоднородности обусловливаются также тепловыми колебаниями. В реальной кристаллической решетке происходит рассеяние «электронных волн» на неоднородностях, что и является причиной электрического сопротивления металлов. Рассеяние «электронных волн» на неоднородностях, связанных с тепловыми колебаниями, можно рассматривать как столкновения электронов с фононами.
Удельное электрическое сопротивление (ρ) металлов можно представить в виде
где ρколеб — сопротивление, обусловленное тепловыми колебаниями решетки, ρприм — сопротивление, обусловленное рассеянием электронов на примесных атомах. Слагаемое ρколеб уменьшается с понижением температуры и обращается в нуль при Т = 0 К. Слагаемое ρприм при небольшой концентрации примесей не зависит от температуры и образует так называемое остаточное сопротивление металла, т. е. сопротивление, которым металл обладает вблизи 0 К.
Расчет электропроводности металлов, выполненный на основе квантовой теории, приводит к выражению для удельной электрической проводимости металла
которое по внешнему виду напоминает классическую формулу для σ, но имеет совершенно другое физическое содержание. Здесь п — концентрация электронов проводимости в металле; — средняя длина свободного пробега электрона, имеющего энергию Ферми, — средняя скорость теплового движения такого электрона, m* — эффективная масса электронов. Выводы, получаемые на основе формулы (15.1), полностью соответствуют опытным данным. Квантовая теория металлов, в частности, объясняет зависимость удельной проводимости от температуры: σ
1/Т (классическая теория дает, что σ
1/√Т), а также аномально большие величины (порядка сотен периодов решетки) средней длины свободного пробега электронов в металле.
Согласно классической теории, средняя скорость теплового движения электронов
√T, поэтому она не смогла объяснить истинную зависимость удельной электрической проводимости σ от температуры. В квантовой теории средняя скорость от температуры практически не зависит, так как доказывается, что с изменением температуры уровень Ферми остается практически неизменным (см. (14.53)). Однако с повышением температуры рассеяние «электронных волн» на тепловых колебаниях решетки (на фононах) возрастает, что соответствует уменьшению средней длины свободного пробега электронов. В области комнатных температур
T -1, поэтому, учитывая независимость от температуры, получим, что сопротивление металлов (R
1/σ) в соответствии с данными опытов растет пропорционально T.
Различие классической трактовки движения электронов проводимости в металле и квантовомеханической трактовки заключается в следующем. При классическом рассмотрении предполагается, что все электроны возмущаются внешним электрическим полем. При квантовомеханической трактовке приходится принимать во внимание, что, хотя электрическим полем также возмущаются все электроны, однако их коллективное движение воспринимается в опыте как возмущение полем лишь электронов, занимающих состояния вблизи уровня Ферми. Кроме того, при классической трактовке в знаменателе формулы (15.1) должна стоять обычная масса электрона т. При квантовомеханической трактовке вместо обычной массы должна быть взята эффективная масса электрона m*. Это обстоятельство является проявлением общего правила, согласно которому соотношения, полученные в приближении свободных электронов, оказываются справедливыми и для электронов, движущихся в периодическом поле решетки, если в них заменить истинную массу m электрона эффективной массой m*.
15.2. Электропроводность полупроводников
Полупроводниками являются кристаллические вещества, у которых при 0 К валентная зона полностью заполнена электронами (см. рис. 14.14, б), а ширина запрещенной зоны невелика. Полупроводники обязаны своим названием тому обстоятельству, что по величине электропроводности они занимают промежуточное положение между металлами и диэлектриками. Однако характерным для них является не величина проводимости, а то, что их проводимость растет с повышением температуры (у металлов она уменьшается).
15.2.1. Собственная проводимость полупроводников
Собственными полупроводниками являются химически чистые полупроводники, а их проводимость называется собственной проводимостью. Примером собственных полупроводников могут служить химически чистые Ge, Si, а также многие химические соединения: InSb, GaAs, CdS и др.
При 0 К и отсутствии других внешних факторов собственные полупроводники ведут себя как диэлектрики. При повышении же температуры электроны с верхних уровней валентной зоны I могут быть переброшены на нижние уровни зоны проводимости I I (рис. 15.1). При наложении на кристалл электрического поля они перемещаются против поля и создают электрический ток. Таким образом, зона I I из-за ее частичного «укомплектования» электронами становится зоной проводимости. Проводимость собственных полупроводников, обусловленная электронами, называется электронной проводимостью или проводимостью n-типа.

Рис. 15.1 Рис. 15.2
Проводимость собственных полупроводников, обусловленная квазичастицами — дырками, называется дырочной проводимостью или проводимостью р-типа.
Таким образом, в собственных полупроводниках наблюдаются два механизма проводимости — электронный и дырочный. Число электронов в зоне проводимости равно числу дырок в валентной зоне, так как последние соответствуют электронам, возбужденным в зону проводимости. Следовательно, если концентрации электронов проводимости и дырок обозначить соответственно ne и nр, то
Проводимость полупроводников всегда является возбужденной, т. е. появляется только под действием внешних факторов (температуры, облучения, сильных электрических полей и т. д.).
В собственном полупроводнике уровень Ферми находится в середине запрещенной зоны (рис. 15.2). Действительно, для переброса электрона с верхнего уровня валентной зоны на нижний уровень зоны проводимости затрачивается энергия активации, равная ширине запрошенной зоны ΔE. При появлении же электрона в зоне проводимости в валентной зоне обязательно возникает дырка. Следовательно, энергия, затраченная на образование пары носителей тока, должна делиться на две равные части. Так как энергия, соответствующая половине ширины запрещенной зоны, идет на переброс электрона и такая же энергия затрачивается на образование дырки, то начало отсчета для каждого из этих процессов должно находиться в середине запрещенной зоны. Энергия Ферми в собственном полупроводнике представляет собой энергию, от которой происходит возбуждение электронов и дырок.
Вывод о расположении уровня Ферми в середине запрещенной зоны собственного полупроводника может быть подтвержден математическими выкладками. В физике твердого тела доказывается, что концентрация электронов в зоне проводимости
где Е2 — энергия, соответствующая дну зоны проводимости (рис. 15.2); ЕF — энергия Ферми; T — термодинамическая температура; С1 — постоянная, зависящая от температуры и эффективной массы электрона проводимости.
Эффективная масса — величина, имеющая размерность массы и характеризующая динамические свойства квазичастиц — электронов проводимости и дырок. Введение в зонную теорию эффективной массы электрона проводимости позволяет, с одной стороны, учитывать действие на электроны проводимости не только внешнего ноля, но и внутреннего периодического поля кристалла, а с другой стороны, абстрагируясь от взаимодействия электронов проводимости с решеткой, рассматривать их движение во внешнем поле как движение свободных части.
Концентрация дырок в валентной зоне
где С2 — постоянная, зависящая от температуры и эффективной массы дырки; Е1 — энергия, соответствующая верхней границе валентной зоны.
Энергия возбуждения в данном случае отсчитывается вниз от уровня Ферми (рис. 15.2), поэтому величины в экспоненциальном множиимеют знак, обратный знаку экспоненциального множителя в (15.3). Так как для собственного полупроводника ne = nр (15.2), то
Если эффективные массы электронов и дырок равны ( ), то C1= C2 и, следовательно, -(E2 — EF)=E1 — EF, откуда
т. е. уровень Ферми в собственном полупроводнике действительно расположен в середине запрещенной зоны. Так как для собственных полупроводников ΔE >> kT, то распределение Ферми — Дирака (14.42) переходит в распределение Максвелла — Больцмана (14.15). Положив в (14.42) E — EF ≈ ΔE/2, получим
Количество электронов, переброшенных в зону проводимости, а следовательно, и количество образовавшихся дырок пропорциональны . Таким образом, удельная проводимость собственных полупроводников
где σ0 — постоянная, характерная для данного полупроводника.
Увеличение проводимости полупроводников с повышением температуры является их характерной особенностью (у металлов с повышением температуры проводимость уменьшается). С точки зрения зонной теории это обстоятельство объяснить довольно просто: с повышением температуры растет чисто электронов, которые вследствие теплового возбуждения переходят в зону проводимости и участвуют в проводимости. Поэтому удельная проводимость собственных полупроводников с повышением температуры растет.
Если представить температурную зависимость удельной проводимости ln σ от 1/Т, то для собственных полупроводников — прямая (рис. 15.3), по наклону которой можно определить ширину запрещенной зоны ΔЕ, а по ее продолжению — σ0 (прямая отсекает на оси ординат отрезок, равный ln σ0. Одним из наиболее широко распространенных полупроводниковых элементов является германий, имеющий решетку типа алмаза, в которой каждый атом связан ковалентными связями с четырьмя ближайшими соседями. Упрошенная плоская схема расположения атомов в кристалле Ge дана на рис. 15.4,
где каждая черточка обозначает связь, осуществляемую одним электроном. В идеальном кристалле при Т = 0 К такая структура представляет собой диэлектрик, так как все валентные электроны участвуют в образовании связей и, следовательно, не участвуют в проводимости. При повышении температуры (или под действием других внешних факторов)

Рис. 15.3. Рис. 15.4.
В результате дырка, так же как и освободившийся электрон, будет двигаться по кристаллу. Движение электронов проводимости и дырок в отсутствие электрического поля является хаотическим. Если же на кристалл наложить электрическое поле, то электроны начнут двигаться против поля, дырки — по полю, что приведет к возникновению собственной проводимости германия, обусловленной как электронами, так и дырками.
В полупроводниках наряду с процессом генерации электронов и дырок идет процесс рекомбинации; электроны переходят из зоны проводимости в валентную зону, отдавая энергию решетке и испуская кванты электромагнитного излучения. В результате для каждой температуры устанавливается определенная равновесная концентрация электронов и дырок, изменяющаяся с температурой, согласно выражению (15.5).
15.2.2. Примесная проводимость полупроводников
Проводимость полупроводников, обусловленная примесями, называется примесной проводимостью, а сами полупроводники — примесными полупроводниками. Примесная проводимость обусловлена примесями (атомы посторонних элементов), а также дефектами типа избыточных атомов (по сравнению со стехиометрическим составом), тепловыми (пустые узлы или атомы в междоузлиях) и механическими (трещины, дислокации и т. д.) дефектами. Наличие в полупроводнике примеси существенно изменяет его проводимость. Например, при введении в кремний примерно 0,001 ат. % бора его проводимость увеличивается примерно в 106 раз.

С точки зрения зонной теории рассмотренный процесс можно представить следующим образом (рис. 15.5, б). Введение примеси искажает поле решетки, что приводит к возникновению в запрещенной зоне энергетического уровня D валентных электронов мышьяка, называемого примесным уровнем. В случае
Германия с примесью мышьяка этот уровень располагается от дна зоны проводимости на расстоянии ΔЕD = 0.013 эВ. Так как ΔЕD > R вх, поэтому Uвых значительно превышает входное напряжение Uвх ( усиление может достигать 10000). Так как мощность переменного тока, выделяемая в Rвых, может быть больше, чем расходуемая в цени эмиттера, то транзистор дает и усиление мощности. Эта усиленная мощность появляется за счет источника тока, включенного в цепь коллектора.
Из рассмотренного следует, что транзистор, подобно электронной лампе, дает усиление и напряжения и мощности. Если в лампе анодный ток управляется напряжением на сетке, то в транзисторе ток коллектора, соответствующий анодному току лампы, управляется напряжением на базе.
Принцип работы транзистора п-р-п-типа аналогичен рассмотренному выше, но роль дырок играют электроны. Существуют и другие типы транзисторов, так же как и другие схемы их включения. Благодаря своим преимуществам перед электронными лампами (малые габаритные размеры, высокие КПД и срок службы, отсутствие накаливаемого катода (поэтому потребление меньшей мощности), отсутствие необходимости в вакууме и т. д.) транзистор совершил революцию в области электронных средств связи и обеспечил создание быстродействующих ЭВМ с большим объемом памяти.
15.4. Контактные и термоэлектрические явления по зонной теории
15.4.1. Работа выхода и термоэлектронная эмиссия

Полная энергия электрона в металле слагается из потенциальной и кинетической энергий. При абсолютном нуле значения кинетической энергии электронов проводимости заключены в пределах от нуля до совпадающей с уровнем Ферми энергии Еmax. На рис. 15.15 энергетические уровни зоны проводимости «вписаны» в потенциальную яму. Для удаления за пределы металла разным электронам нужно сообщить неодинаковую энергию. Так, электрону, находящемуся на самом нижнем уровне зоны проводимости, необходимо сообщить энергию ЕР0; для электрона, находящегося на уровне Ферми, достаточна энергия ЕР0 — Еmax = ЕР0 — EF.
Наименьшая энергия, которую необходимо сообщить электрону для того, чтобы удалить его из твердого или жидкого тела в вакуум, называется работой выхода. Работу выхода принято обозначать через eφ, где φ — величина, называемая потенциалом выхода. Работа выхода электрона из металла определяется выражением
При повышении температуры часть электронов проводимости имеет энергию достаточную для преодоления потенциального барьера на границе металла. Испускание электронов нагретым металлом называется термоэлектронной эмиссией.
Этот эффект используется в электронных лампах, где катод разогревается до высоких температур. Измеряя вольт-амперную характеристику двухэлектродной лампы (катод, анод) при разных температурах катода и анодного напряжения можно исследовать термоэлектронную эмиссию.
Исходя из квантовых представлений, Дэшман получил (1923 г.) для тока насыщения формулу
Здесь eφ – работа выхода, А –константа. Температурный ход тока насыщения эта передает вполне удовлетворительно. Формула (15.10) называется формулой Ричардсона — Дэшмана.
15.4.2. Контактная разность потенциалов
Если привести два разных металла в соприкосновение, между ними возникает разность потенциалов, которая называется контактной. В результате в окружающем металлы пространстве появляется электрическое поле.
Контактная разность потенциалов обусловлена тем, что при соприкосновении металлов часть электронов из одного металла переходит в другой. В верхней части рис. 15.16 изображены два металла до приведения их в соприкосновение и даны их графики потенциальной энергии электрона. Уровень Ферми в первом металле лежит, по предположению, выше, чем во втором. . В нижней части рис. 15.16 изображены два металла после приведения их в соприкосновение и даны их графики потенциальной энергии электрона. Естественно, что при возникновении контакта между металлами электроны с самых высоких уровней в первом металле станут переходить на более низкие свободные уровни второго металла. В результате потенциал первого металла возрастет, а второго — уменьшится. Соответственно потенциальная энергия электрона в первом металле уменьшится, а во втором

Разность потенциалов (15.11), обусловленная различием работ выхода контактирующих металлов, называется внешней контактной разностью потенциалов. Чаще говорят просто о контактной разности потенциалов, подразумевая под ней внешнюю.
Если уровни Ферми для двух контактирующих металлов неодинаковы, то между внутренними точками металлов наблюдается внутренняя контактная разность потенциалов которая, как следует из рисунка, равна
В квантовой теории доказывается, что причиной возникновения внутренней контактной разности потенциалов является различие концентраций электронов в контактирующих металлах. ∆φ» зависит от температуры Т контакта металлов (поскольку наблюдается зависимость ЕF от Т), обусловливая термоэлектрические явления. Как правило, ∆φ»
Движение электрона в поле кристалла дрейфовое уравнение
17. Движение носителей заряда в полупроводниках (дрейф, диффузия).
В соответствии с зонной моделью в полупроводнике имеются два вида подвижных носителей заряда: электроны в зоне проводимости и дырки в валентной зоне. Они могут двигаться под действием температуры ( тепловое движение), электрического поля ( дрейф) и градиента концентрации ( диффузия).
Можно представить, что свободные электроны движутся хаотически через кристаллическую решетку в различных направлениях, сталкиваясь друг с другом и с узлами решетки. При тепловом движении при отсутствии градиента температуры движение системы электронов полностью беспорядочно, так что результирующий ток в любом направлении равен нулю. Столкновения с узлами решетки приводят к обмену энергией между электронами и атомными ядрами, образующими решетку. Воздействие решетки на движение электронов в первом приближении было учтено ранее путем введения эффективной массы. Далее будет более подробно рассмотрено влияние узлов решетки на движение носителей заряда в полупроводнике.
1.5.1. Дрейф свободных носителей заряда. Дрейфом называют направленное движение носителей заряда под действием электрического поля.
Если к полупроводниковому кристаллу приложить слабое электрическое поле 
Рис.1.13. Движение электронов в полупроводнике под воздействием внешнего электрического поля
Отметим, что составляющая скорости, обусловленная полем, представляет собой небольшое возмущение хаотической тепловой скорости 

Результирующая скорость носителей в направлении приложенного электрического поля называется дрейфовой скоростью 

Коэффициент 

где 
Из уравнения (1.1) можно определить плотность тока 

Совершенно аналогичные рассуждения применимы и к дыркам. Подвижность дырок обозначается 

Полная плотность тока дрейфа может быть записана в виде суммы электронной и дырочной составляющих:

Член в скобках в уравнении (1.39) определяется как удельная проводимость полупроводника 

В примесных полупроводниках обычно основную роль играет только одно из слагаемых формулы (1.40), так как разница концентраций двух типов подвижных носителей заряда в них очень велика.
Поскольку удельное сопротивление 

Зависимость удельного сопротивления кремния при комнатной температуре от концентраций примесей доноров или акцепторов приведена на рис.1.14. График построен на основе большого числа измерений удельного сопротивления образцов кремния, содержащих примеси. Этот график широко используется в полупроводниковой промышленности.
Рис.1.14. Зависимость удельного сопротивления кремния от концентрации примеси при температуре 300 К
1.5.3. Диффузия свободных носителей заряда. Рассмотрим еще один вид движения свободных носителей заряда, который возникает под действием градиента концентраций. Такое движение называется диффузией, а ток созданный диффузией носителей заряда называют диффузионным током. В металлах вследствие их высокой проводимости диффузионный ток не играет заметной роли. В полупроводниках же с их более низкой проводимостью и возможностью неоднородного распределения концентраций примесей диффузионный ток играет существенную роль и составляет значительную долю в общем токе.
Наиболее часто в полупроводниках диффузионный ток возникает из-за различия концентраций на отдельных участках. Рассмотрим электронный полупроводник, состоящий из двух участков с различной концентрацией электронов. Предположим, что полупроводник находится в равновесии, т . е . отсутствуют внешнее электрическое поле и перепад температур. Очевидно, что на границе участков возникает градиент концентраций, под действием которого электроны начинают диффундировать из участка с избыточной концентрацией в участок с меньшей концентрацией. Плотность тока диффузии в соответствии с первым законом Фика будет пропорциональна градиенту концентрации

где 

Первый знак «минус» в формуле (1.43) указывает, что ток диффузии направлен в сторону убывания концентрации электронов. Коэффициент диффузии электронов связан с их подвижностью формулой Эйнштейна

Для дырок плотность тока диффузии и коэффициент диффузии соответственно равны


Знак «минус» в выражении (1.45) появляется из-за положительного заряда дырок.
Следует отметить отличие диффузии заряженных частиц от диффузии нейтральных частиц. Так диффузия нейтральных частиц продолжается до полного выравнивания концентраций во всем объеме. Диффузия же заряженных частиц протекает несколько иначе, поскольку диффундирующие частицы переносят заряд. В результате, внутри полупроводника около границ участков с различной концентрацией нарушается электрическая нейтральность и возникает внутреннее электрическое поле, препятствующее дальнейшей диффузии. Возникающие в результате диффузии внутренние электрические поля играют существенную роль в работе твердотельных приборов. Эти поля будут подробнее рассмотрены в главе 2.
Помимо описанной выше диффузии носителей заряда, возникающей из-за градиента концентраций, в полупроводниках возможна диффузия из-за различия энергий носителей заряда. Так например, локальное нагревание участка полупроводника может вызвать диффузию носителей из участка с более высокой температурой в участок с более низкой температурой.
1.5.4. Полный ток в полупроводниках. В общем случае направленное движение электронов и дырок в полупроводниках обусловлено двумя процессами: дрейфом под действием электрического поля и диффузией под действием градиента концентраций. Поэтому полная плотность тока в полупроводниках содержит четыре составляющих:

где индексы dr и dif относятся соответственно к дрейфовым и диффузионным составляющим плотности тока.
В одномерном случае, когда движение носителей заряда происходит только вдоль оси х, составляющие плотности тока описываются формулами (1.39), (1.43), (1.45). Для наглядности приведем эти формулы.
Дрейфовые составляющие плотности тока


Диффузионные составляющие плотности тока


Полупроводник, в котором протекает ток, находится в неравновесном состоянии, поэтому для описания процессов в нем можно использовать квазиуровни Ферми (1.29) и (1.30). Применение квазиуровней Ферми позволяет упростить выражения для составляющих плотности тока. Так электронная составляющая плотности тока, представляющая собой сумму дрейфовой и диффузионной составляющих, определяется через квазиуровни Ферми следующим образом:

Аналогично для дырок

Формулы (1.52) и (1.53) показывают, что полная плотность тока для каждого типа свободных носителей заряда пропорциональна градиенту квазиуровня Ферми соответствующего типа носителей вдоль оси х. Это компактное написание может быть очень удобным при использовании энергетических зонных диаграмм для описания полного тока в твердотельном приборе.
В заключение следует отметить, что обычно в полупроводнике превалирует какая-нибудь одна составляющая тока, поэтому выражение (1.47) используется достаточно редко.
http://pandia.ru/text/78/219/15086.php
http://www.mynameisgyry.narod.ru/4-17.html