Движение материальной точки задано уравнением орты осей

Движение материальной точки задано уравнением r(t)=i(A+Bt²)+jCt, где A=10 м, В= — 5 м/с², С=10 м/с. Начертить траекторию точки. Найти выражения v(t) и a(t).

Ваш ответ

решение вопроса

Похожие вопросы

• Все категории
• экономические 43,299
• гуманитарные 33,630
• юридические 17,900
• школьный раздел 607,256
• разное 16,836

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

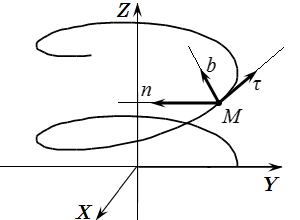
Оси естественного трехгранника Френе

Введение

На странице “Кинематика материальной точки” мы установили, что вектор скорости движения точки направлен по касательной к траектории. Вектор ускорения лежит в соприкасающейся плоскости и его можно разложить на две составляющие. Одна составляющая направлена по касательной к траектории. Вторая составляющая направлена перпендикулярно касательной, в сторону мгновенного центра кривизны траектории.

В некоторых случаях удобно ввести систему координат, связанную с текущим положением точки. Рассмотрим точку в определенный момент времени. Считаем, что нам известна траектория ее движения. Проведем через точку три прямых – касательную к траектории, главную нормаль и бинормаль. Главная нормаль перпендикулярна касательной и направлена в сторону мгновенного центра кривизны траектории. Бинормаль перпендикулярна касательной и главной нормали. Выберем систему координат с началом в точке и осями, направленными вдоль этих прямых. Такую систему координат называют естественным трехгранником Френе. Оси этой системы координат называются осями естественного трехгранника.

Орты естественного трехгранника

Пусть , и – единичные векторы, направленные вдоль касательной, главной нормали и бинормали к траектории, соответственно. Эти векторы являются ортами выбранной нами системы координат или ортами естественного трехгранника. Рассмотрим вопрос о выборе направления этих векторов.

Единичный вектор направлен вдоль касательной к траектории. Поэтому можно выбрать два взаимно противоположных направления. Самый удобный способ – это направить вдоль вектора скорости точки. Тогда
.
Однако, это не всегда можно сделать. Встречаются случаи, когда траектория движения заранее известна, а скорость – нет. Например, при движении точки по желобу внутри твердого тела под действием внешних сил. В таких случаях направление вектора выбирают заранее. Например, в сторону возрастания дуговой координаты.

Направление единичного вектора главной нормали определено однозначно. Он направлен перпендикулярно , в сторону мгновенного центра кривизны траектории.

Единичный вектор бинормали направлен перпендикулярно векторам и так, чтобы три вектора , и образовали правостороннюю систему координат:
.

Скорость и ускорение точки в трехграннике Френе

Применим формулы, которые мы вывели на странице “Кинематика материальной точки”.

То есть, в естественном трехграннике с ортами , скорость имеет одну компоненту:
.
Проекции вектора скорости на оси и трехгранника равны нулю. Проекцию скорости на направление единичного вектора касательной к траектории : , иногда называют алгебраической величиной скорости. Она отличается от модуля скорости только тем, что может иметь отрицательное значение: . При , скорость направлена вдоль вектора . При – в противоположную сторону.

Здесь и далее модуль скорости мы обозначаем либо символом с прямыми скобками , , либо просто символом без стрелки :
.

Ускорение имеет две компоненты:
,
Через них выражается касательное и нормальное ускорения:
.
Они являются проекциями вектора ускорения на оси и естественного трехгранника:
.
Их можно выразить через компоненту скорости и радиус кривизны траектории :
.
Компонента может быть как положительной (вектор сонаправлен с ), так и отрицательной (вектор противоположен ): . Компонента всегда положительна либо равна нулю: .

Проекция вектора ускорения на ось равна нулю:
.

Как определить оси естественного трехгранника

Далее мы считаем, что у нас есть неподвижная система координат . Материальная точка совершает движение. Требуется найти оси естественного трехгранника. То есть определить проекции ортов , и в системе координат .

Для координатного и векторного способов задания движения

Для координатного и векторного способов задания движения точки, формулы для определения ортов представлены на странице “Кинематика материальной точки”. На странице “Координатный способ задания движения точки” разобран пример вычисления компонентов векторов .

То есть, чтобы определить орты естественного трехгранника, нужно найти компоненты векторов скорости и нормального ускорения , применяя следующие формулы:
;
;
;
.

Далее определяем орты естественного трехгранника:
;
;
.

Для естественного способа задания движения

При естественном способе задания движения точки нам известна траектория ее движения. Поэтому перед нами стоит задача – по известной траектории, определить орты естественного трехгранника. Если траектория представляет собой простую геометрическую фигуру, например окружность, то определить векторы , и можно геометрически.

В общем, и более сложном случае, нужно представить уравнение траектории в параметрическом виде. Для этого вводим параметр . Это можно сделать многими способами. Поэтому желательно выбрать наиболее удобное представление.

Пусть, например, траекторией движения является эллипс, лежащий в плоскости :
.
Наиболее удобное параметрическое представление можно получить, если воспользоваться тригонометрической формулой:
.
Тогда уравнение траектории имеет вид:

Здесь – параметр.

Это не единственный способ получить параметрическое представление. Можно, например, разрешить уравнение эллипса относительно :
.
Применяя эту формулу, получим другое параметрическое представление:

Далее считаем, что эти параметрические уравнения описывают движение материальной точки, в котором параметр играет роль времени. Тогда, для определения осей трехгранника, можно применить формулы, применяемые для векторного и координатного способов задания движения. Вычисленные, таким образом, скорость и ускорение будут зависеть от выбранного параметрического представления. Но геометрические характеристики траектории, такие как орты , , и радиус кривизны траектории не зависят от выбранного параметрического представления.

Итак, чтобы найти орты естественного трехгранника по заданной траектории движения, нужно представить уравнение траектории в параметрическом виде и применить формулы, применяемые при координатном способе задания движения.

Пример определения ортов естественного трехгранника

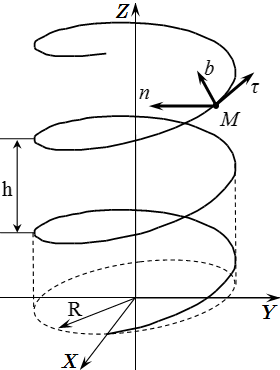
Найти единичные векторы в направлении осей естественного трехгранника, а также радиус кривизны траектории, для цилиндрической винтовой линии с радиусом основания и шагом .

Выберем систему координат . Ось направим вдоль оси винтовой линии. Тогда уравнение линии можно представить в следующем параметрическом виде:
(1)
Здесь – параметр; . Если взять проекцию точки линии, на плоскость , то – это угол между осью и проекцией . При увеличении на , координаты и точки возвращаются в первоначальной положение, а координата увеличивается на .

Считаем, что уравнения (1) описывают движение точки по винтовой линии. Определяем кинематические величины для такого движения.

Дифференцируя уравнения (1) по , находим компоненты вектора скорости:
;
;
.

Квадрат скорости:
.
Модуль скорости:
.

Единичный вектор в направлении касательной к траектории:
.
Мы выбрали направление вектора , совпадающим с направлением скорости. Поэтому
.

Дифференцируя компоненты вектора скорости по , находим компоненты вектора ускорения:
;
;
.

Проекция ускорения на направление вектора :

.
Этот результат можно получить и более простым способом. Для этого учтем, что модуль скорости и, следовательно , не зависит от . Тогда:
.
Вектор касательного ускорения:
.

Вектор нормального ускорения:

.

Квадрат вектора нормального ускорения:
.
Модуль вектора нормального ускорения:
.

Радиус кривизны траектории:
.

Единичный вектор в направлении главной нормали траектории:
.

Единичный вектор в направлении бинормали:

.

Автор: Олег Одинцов . Опубликовано: 14-03-2016 Изменено: 27-01-2020

Уравнение движения материальной точки

Движение материальной точки в пространстве – это изменение ее положения относительно других тел с течением времени.

Имеет смысл говорить только о движении в некоторой системе отсчета.

Система отсчета. Системы координат

Точки, располагаемые в пустом пространстве, не различаются. Поэтому о точке рассуждают при условии нахождения в ней материальной точки. Определить ее положение можно при помощи измерений в системе координат, где и проводится нахождение пространственных координат. Если рассматривать в виде примера поверхность Земли, то следует учитывать широту и долготу располагаемой точки.

В теории используется декартова прямоугольная система координат, где определение точки возможно при наличии радиус-вектора r и трех проекций x , y , z – ее координат. Могут быть применены другие:

• сферическая система с положением точек и ее радиус-вектором, определенных координатами r , υ , φ ;
• цилиндрическая система с координатами p , z , α ;
• на полярной плоскости с параметрами r , φ .

В теории зачастую не принимают во внимание реальную систему отсчета, а сохраняют только ту, которая представляет собой ее математическую модель, применяемую во время практических измерений.

Кинематическое уравнение движения материальной точки

Любая система отсчета или координат предполагает определение координат материальной точки в любой момент времени.

При условии положения и определения материальной точки в данной системе отсчета считается, что ее движение задано или описано.

Это возможно при использовании кинематического уравнения движения:

Аналитически положение точки определяется совокупностью трех независимых между собой чисел. Иначе говоря, свободная точка имеет три степени свободы движения.

Ее перемещение по уравнению ( 1 ) определено, если имеется указанное положение в любой момент времени t . Для этого следует задавать декартовы координаты точки в качестве однозначных и непрерывных функций времени:

x ( t ) = x , y ( t ) = y , z ( t ) = z ( 2 ) .

Прямоугольные декартовы координаты x , y , z — это проекции радиус-вектора r ¯ , проведенного из начала координат. Очевидно, что длину и направление r ¯ можно найти из соотношений, где a , β , γ являются образованными радиус-вектором углами с координатными осями.

Равенства ( 2 ) считают кинематическими уравнениями движения материальной точки в декартовых координатах.

Они могут быть записаны в другой системе координат, которая связана с декартовой взаимно однозначным преобразованием. Если движение точки происходит в плоскости О х у , тогда применимы полярные координаты r , φ , относящиеся к декартовым преобразованиям. Данный случай подразумевает использование уравнения движения точки следующего вида:

r = r ( t ) , φ = φ ( t ) ( 3 ) .

Кинематическое уравнение движения точки в криволинейных координатах q 1 , q 2 , q 3 , связанных с декартовыми преобразованиями вида x = x ( q 1 , q 2 , q 3 ) , y = y ( q 1 , q 2 , q 3 ) , z = z ( q 1 , q 2 , q 3 ) ( 4 ) , записывается как

q 1 = q 1 ( t ) , q 2 = q 2 ( t ) , q 3 = q 3 ( t ) ( 5 ) .

Кривая радиус-вектора, описываемая концом вектора r при движении точки, совпадает с ее траекторией. Параметрическое уравнение траектории с t представлено кинематическими уравнениями ( 2 ) , ( 5 ) . Чтобы получить координатное уравнение траектории следует исключить время из кинематических уравнений.

Определение движения точки возможно с помощью задания траектории и мгновенного положения точки на ней. Ее положение на кривой определяется с помощью указания только одной величины: расстояния вдоль кривой от некоторой начальной точки с положительным направлением:

Это и есть уравнение движения точки по траектории. Способ его задания относят к естественному или траекторному.

Понятия координатного и естественного способа задания движения точки физически эквивалентны. С математической стороны это рассматривают как возможность применения разных методов, исходя из случая математической задачи.

Задание такого закона возможно аналитическим, графическим путем или с использованием таблицы, последние два из которых зачастую рассматривают в виде графиков и расписаний движений поездов.

Дано уравнение движения материальной точки x = 0 , 4 t 2 . Произвести запись формулы зависимости υ x ( t ) , построить график зависимости скорости от времени. На графике отметить площадь, численно равную пути, пройденному точкой за 4 секунды, произвести вычисление.

Дано: x = 0 , 4 t 2 , t = 4 c

Найти: υ x ( t ) , S — ?

Решение

При решении необходимо учитывать зависимость скорости от времени:

υ x = υ 0 x + a x t .

Зависимость координаты от времени и сравнение уравнения с заданным принимает вид:

x = x 0 + υ 0 x t + a x t 2 2 , x = 0 , 4 t 2 .

Очевидно, что x 0 = 0 , υ 0 x = 0 , a x = 0 , 8 м / с 2 .

После подстановки данных в уравнение:

Определим точки, изобразим график:

υ x = 0 , t = 0 , υ x = 4 , t = 5

Путь, по которому двигалось тело, равняется площади фигуры, ограниченной графиком, и находится с помощью формулы: