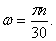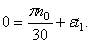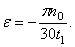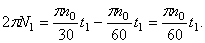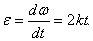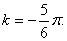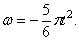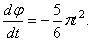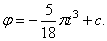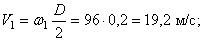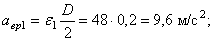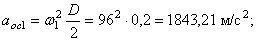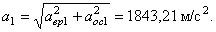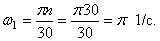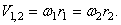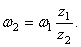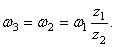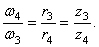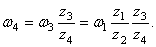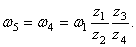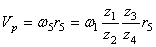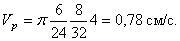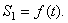Движение тела вокруг неподвижной оси задано уравнением

Движение тела вокруг неподвижной оси задано уравнением

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ

Кинематика вращения тела вокруг неподвижной оси

1. Краткие сведения из теории

Уравнение вращательного движения твердого тела вокруг неподвижной оси имеет вид

. (40)

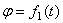
Отсчет угла ведется от выбранного начала. При этом углам, отложенным в направлении движения часовой стрелки, придается знак “минус”, а углам противоположного направления – знак “плюс”.

Угол поворота выражается в радианах. Иногда угол поворота определяется числом оборотов N. Зависимость между и N следующая .

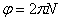
Угловая скорость тела:

(41)

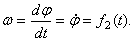
Знак производной 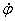дает возможность установить происходит ли вращение тела в положительном направлении отсчета угла поворота (знак “плюс”) или в обратную сторону (знак “минус”). Единица измерения угловой скорости – радиан в секунду (или 1/с).

Иногда угловую скорость характеризуют числом оборотов в минуту и обозначают буквой n . Зависимость между и n имеет вид

Угловое ускорение тела:

(42)

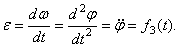
Знак производной 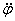дает возможность установить является ли вращение тела в данный момент времени ускоренным или замедленным. Если знаки и одинаковы, тело вращается ускоренно, а если их знаки различны – замедленно. Единица измерения углового ускорения – радиан на секунду в квадрате (или 1/с 2 ).

Траекториями точек тела, не лежащих на оси вращения, являются окружности с центрами на оси вращения и радиусами, равными кратчайшему расстоянию от этих точек до оси вращения.

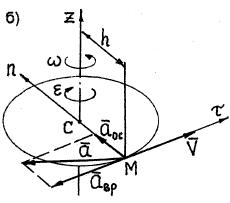
Модуль скорости любой точки тела, находящейся на расстоянии h от оси вращения (рис. 18), определяется по формуле

. (43)

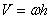
Направлена скорость точки по касательной к описываемой точкой окружности в сторону движения.

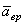
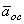
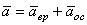
Ускорение любой точки тела состоит из двух составляющих – вращательного и осестремительного ускорений:

.

Модуль вращательного ускорения точки определяется по формуле

. (44)

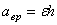
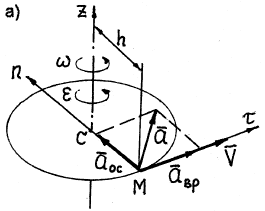
Вращательное ускорение направлено по касательной к описываемой точкой окружности в ту же сторону, что и его скорость, если вращение тела ускоренное (рис. 18, а) и в сторону, противоположную скорости, если вращение замедленное (рис.18, б).

Модуль осестремительного ускорения определяется по формуле

. (45)

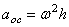
Осестремительное ускорение всегда направлено по радиусу окружности от точки к центру окружности (рис. 18).

Модуль полного ускорения точки определяется по формуле

(46)

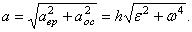
2. Основные типы задач кинематики вращения тела вокруг оси

В зависимости от того, что задано в условии задачи и что требуется определить, различают следующие два основных типа задач.

1. Исследуется движение тела в целом. В этих задачах вначале нужно получить законы (40)–(42) и, используя связь между ними, определить требуемую величину (см. примеры 17 и 18).

2. Требуется определить скорости и ускорения отдельных точек тела. Для решения задач этого типа вначале надо установить кинематические характеристики движения всего тела в целом, т.е. найти , и . После чего по формулам (43), (44), (45), (46) определить скорости и ускорения точек тела (см. пример 19).

Пример 17. Пропеллер самолета, делающий 1200 об / мин , после выключения двигателя останавливается через 8 с. Сколько оборотов сделал пропеллер за это время, если считать его вращение равнозамедленным?

Вначале получим законы вращения пропеллера (40), (41) и (42). По условию задачи пропеллер вращается равнозамедленно , из этого следует, что

.

, (47)

(48)

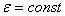
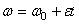
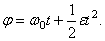
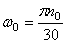
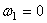
Начальной угловой скоростью при замедленном вращении будет та, которую пропеллер имел до выключения двигателя. Следовательно, . В момент остановки при t₁ = 8 сек. угловая скорость тела . Подставляя эти значения в уравнение (47), получим

Отсюда

Если обозначить число сделанных пропеллером за время t₁ оборотов через N₁, то угол поворота за то же время будет равен

.

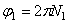
Подставляя найденные значения и в уравнение (48), получим

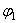
Отсюда 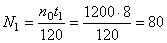оборотов.

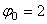
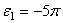
Пример 18. Найти закон вращения тела вокруг оси, если известны следующие данные: угловая скорость изменяется пропорционально t 2 , начальный угол поворота рад, для заданного момента времени t₁ = 3 с угловое ускорение 1/с 2 .

По условию задачи модуль угловой скорости изменяется пропорционально t 2 . Обозначая неизвестный коэффициент пропорциональности буквой k , имеем

. (49)

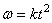
Найдем , беря производные по времени от обеих частей равенства (49),

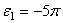
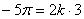
Определим коэффициент k из условия, что при t₁ = 3 сек. угловое ускорение 1/с 2 : или

Подставляя значение k в уравнение (49), получим

Учитывая, что 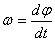, будем иметь

Умножая обе части этого уравнения на dt и интегрируя, находим

В начальный момент при t = 0, 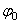= 2 рад, следовательно, c = 2.

Таким образом, 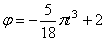радиан.

Пример 19. В период разгона ротор электродвигателя вращается по закону 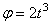, где t в сек, в рад.

Определить в конце 4-й секунды линейную скорость, вращательное, осестремительное и полное ускорения точки, лежащей на ободе ротора, если диаметр ротора D = 40 см .

По заданному уравнению вращения ротора находим его угловую скорость и угловое ускорение , .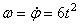

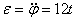
Подставляя значение t₁ = 4 сек в выражение для и , найдем

1/с,

1/с 2 .

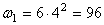
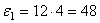
Определим модули линейной скорости, вращательного и осестремительного ускорений в этот же момент времени по формулам (43), (44) и (45)

Модуль полного ускорения точки обода ротора определим по формуле (46)

3. Определение скоростей и ускорений в случаях, когда вращающееся тело входит в состав различных механизмов

Рассмотрим механизмы с поступательным и вращательным движением звеньев. Решение задачи начинают с определения скоростей точек того звена, для которого движение задано. Затем рассматривают звено, которое присоединено к первому звену и т.д. В результате определяют скорости точек всех звеньев механизма. В такой же последовательности определяют и ускорения точек.

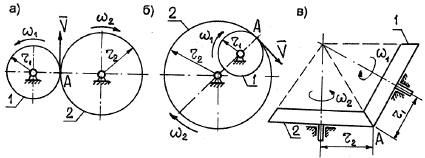
Передача вращения от одного вращающегося тела, называемого ведущим, к другому, называемому ведомым, может осуществляться при помощи фрикционной или зубчатой передачи (рис. 19).

Во фрикционной передаче вращение передается вследствие действия силы трения в месте контакта соприкасающихся колес, в зубчатой передаче – от зацепления зубьев. Оси вращения ведущего и ведомого колес могут быть параллельными (рис. 19, а, б) или пересекаться (рис. 19, в). В рассмотренных случаях линейные скорости точек А соприкасания колес одинаковы, их модули определяются так:

. (50)

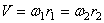
Отсюда 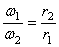. (51)

То есть угловые скорости колес фрикционной или зубчатой передачи обратно пропорциональны радиусам колес.

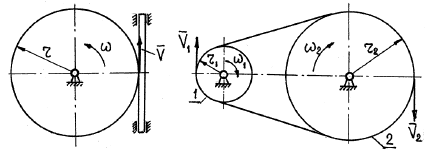
При преобразовании вращательного движения в поступательное (или наоборот) часто используют зацепление зубчатого колеса с зубчатой рейкой (рис. 20). Для этой передачи выполняется условие: .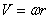

Кроме фрикционной и зубчатой передач, существует передача вращения при помощи гибкой связи (ремня, троса, цепи) (рис. 21).

Так как модули скоростей всех точек ремня одинаковы и ремень не скользит по поверхностям шкивов, то соотношения (50) и (51) относятся и к ременной передаче.

Пример 20. В механизме домкрата при вращении рукоятки ОА шестерни 1, 2, 3, 4, 5 приводят в движение зубчатую рейку ВС домкрата (рис. 22).

Определить скорость рейки, если рукоятка ОА делает 30 оборотов в минуту ( n = 30 об /мин). Числа зубцов шестерен: z₁ = 6, z₂ = 24, z₃ = 8, z₄ = 32; радиус пятой шестерни r₅ = 4 см .

Так как рукоятка ОА жестко соединена с шестерней 1, то последняя делает тоже 30 об /мин или

Модули скоростей точек соприкасания зубчатых колес 1 и 2 одинаковы для точек обоих колес и определяются по формуле (50)

Отсюда 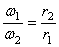(см. также (51)).

Так как числа зубьев пропорциональны радиусам колес, то .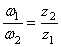

Отсюда

Шестерни 2 и 3 жестко соединены между собой, поэтому

Для находящихся в зацеплении колес 3 и 4 на основании (51) можно записать

Отсюда

Шестерни 4 и 5 жестко соединены между собой, поэтому

Модули скоростей точек соприкосновения зубчатой рейки ВС и шестерни 5 одинаковы, поэтому

или

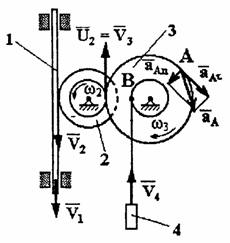
Пример 21. Рейка 1, ступенчатое колесо 2 с радиусами R ₂ и r ₂ и колесо 3 радиуса R ₃ , скрепленное с валом радиуса r₃, находятся в зацеплении; на вал намотана нить с грузом 4 на конце (рис.23). Рейка движется по закону

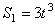
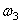
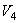
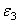
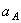
Дано: R ₂ =6 см, r₂=4 см, R₃=8 см, r₃=3 см, ( S — в сантиметрах, t — в секундах), А — точка обода колеса 3, t ₁ =3 с. Определить: , , , в момент времени t = t₁.

Указания. Пример 21 — на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что, когда два колеса находятся в зацеплении, скорость точки зацепления каждого колеса одна и та же, а когда два колеса связаны передачей, то скорости всех точек ремня и, следовательно, точек, лежащих на ободе каждого из этих колес, в данный момент времени численно одинаковы, при этом считается, что ремень по ободу колес не скользит.

Условимся обозначать скорости точек, лежащих на внешних ободах колес (радиуса R ₁ ), через V₁, а точек, лежащих на внутренних ободах (радиуса r ₁ ), через U₁.

1. Зная закон движения рейки 1, находим ее скорость:

. ( 52 )

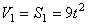
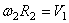
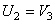
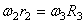
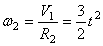
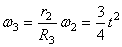
Так как рейка и колесо 2 находятся в зацеплении, то V ₂ = V₁ или . Но колеса 2 и 3 тоже находятся в зацеплении, следовательно, или . Из этих равенств находим:

, . (53)

Тогда для момента времени t₁ = 3 сек. получим 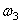= 6,75 с -1 .

2. Определяем V ₄ . Так как 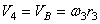, то при t₁=3 c ек . V ₄ = 20 ,25 см/с.

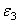
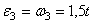
3. Определяем . Учитывая второе из равенств (53), получим .

Тогда при t₁ = 3 сек. 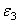= 4,5 с -2 .

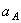
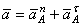
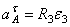
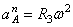
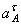
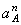
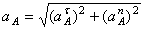
4. Определяем . Для точки А , где численно , . Тогда для момента времени t₁ = 3 сек. имеем = 36 см/с2, = 364,5 см/с2.

= 366,3 см/с 2 ,

Все скорости и ускорения точек, а также направления угловых скоростей показаны на рис.2.

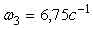
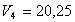
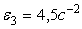
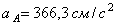
Ответ: , см/ с , , .

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Движение тела вокруг неподвижной оси задано уравнением

Вращение тела вокруг неподвижной оси задано уравнением `varphi = 2t — 4t^3` (`varphi`- в рад, t — в с). Начало вращения тела при `t = 0` Положительные углы отсчитываются в направлении стрелки (см. рис.) В каком направлении поворачивается тело в момент времени `t = 5с`?

Вращение тела вокруг неподвижной оси задано уравнением `varphi= Asin pit` (`varphi` — в рад, t — в с). Начало вращения тела при `t = 0` Положительные углы отсчитываются в направлении стрелки (см. рис.) В каком направлении поворачивается тело в момент времени` t = 1,25с`?

Тело вращается вокруг неподвижной оси с угловым ускорением `beta = 2t^2` В начальный момент времени тело покоится Определить закон изменения угловой скорости тела (`omega`- в рад/с, `beta` — в рад/`с^2` `t` — в с)

Движение точки по окружности описывается уравнением `s = 2t^3` (s — в м, t — в с). Как изменяется со временем угол между векторами полного и тангенциального ускорения точки?

Какие из перечисленных выражений совпадают в случае свободного падения тела с выражением `(dv)/(dt)` (`vectau` — единичный вектор, касательный к траектории и направленный по движению)

Применима ли для вычисления угла поворота тела формула `varphi = omega * t` в случаях: (`omega` — в рад/ с, t- в с)

Вращение тела вокруг неподвижной оси задано уравнением `varphi = 2pi(6t — 3t^2)` (`varphi` — в рад, t-вс). Начало вращения тела при `t = 0`. Сколько оборотов сделает тело до момента изменения направления вращения?

Человек шёл из деревни в город со скоростью `5(км)/ч`. Обратно он возвращался с покупками той же дорогой, но со скоростью `3(км)/ч` . Определите в `(км)/ч` среднюю скорость пешехода за всё время движения.

Движение точки М (см. рис.) задано уравнением `x = 2t^2 — 4t^3` (x — в м, t — в с). Начало движения точки при ` t = 0`. Указать направления движения точки в следующие моменты времени:

Математический маятник совершает гармонические колебания. Отличны ли от нуля в средней точке траектории маятника

Прямолинейное движение материальной точки задано уравнением `x = 3t — 4t^3` (x — в м, t — в с). Начало движения точки при `t = 0`. Как изменяется модуль скорости в следующие моменты времени:

Математический маятник совершает гармонические колебания. Отличны ли от нуля в крайней точке траектории маятника.

Прямолинейное движение материальной точки задано уравнением `x = 20t — 5t^2` (x-в м, t — в с). Начало движения точки при ` t = 0`. Совпадают ли координата и пройденный точкой путь в следующие моменты времени:

Два грузовика движутся по прямому участку дороги: первый — со скоростью `vecupsilon`, второй — со скоростью `-4vecupsilon`. Какова скорость второго грузовика относительно первого?

Два грузовика движутся по прямому участку дороги: первый — со скоростью `vecupsilon`. второй — со скоростью `3vecupsilon` Модуль скорости первого грузовика относительно второго равен .

Прямолинейное движение материальной точки задано уравнением `x = 3t — t^2` (x — в м, t — в с). Начало движения точки при `t = 0`. Достигнет ли точка следующих координат:

Точка движется равномерно по окружности. Начало её радиус-вектора `vectau` совпадает с центром окружности. Отличны ли от нуля выражения:

Какой знак связывает выражения `abs((dvecupsilon)/(dt))` и `abs((dupsilon)/(dt))` при произвольном движении точки?

Применима ли для вычисления углового ускорения тела формула `beta =omega/t` в случаях: (`omega` — в рад/с: t — в с)

Является ли движение точки обязательно прямолинейным в следующих случаях:

Можно ли утверждать, что точка движется без ускорения в случаях:

Вращение тела вокруг неподвижной оси задано уравнением `varphi = Asin((pit)/4)` — в рад, t — в с). Начало вращения тела при t = 0 Как изменяется величина угловой скорости в следующие моменты времени:

Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях – решение задачи

Основные законы и формулы, применяемые при решении задач

Вращательное движение вокруг неподвижной оси

Рассмотри твердое тело, вращающееся вокруг неподвижной оси z . Сделаем рисунок. Ось вращения направим перпендикулярно плоскости рисунка, на нас. Пусть φ – угол поворота тела вокруг оси, отсчитываемый от некоторого начального положения. За положительное направление выберем направление против часовой стрелки. Угловая скорость ω равна производной угла поворота по времени t :
.
При , тело вращается против часовой стрелки; при – по часовой. Вектор угловой скорости направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

Угловое ускорение ε равно производной угловой скорости по времени:
.
Вектор углового ускорения также направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

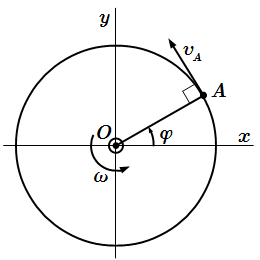
Скорость точки при вращательном движении тела вокруг неподвижной оси

Рассмотрим точку A , принадлежащую твердому телу. Опустим из нее перпендикуляр OA на ось вращения. Пусть – расстояние от точки до оси. Траекторией движения точки A является окружность (или дуга) с центром в точке O радиуса .

Абсолютное значение скорости точки A определяется по формуле:
.
Вектор скорости направлен по касательной к траектории (окружности), перпендикулярно отрезку OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор угловой скорости .

Касательное (или тангенциальное) ускорение точки A определяется аналогично скорости:
.
Оно направлено по касательной к окружности, перпендикулярно OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор углового ускорения .

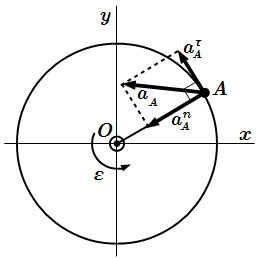
Ускорение точки при вращательном движении тела вокруг неподвижной оси

Нормальное ускорение всегда направлено к центру окружности и имеет абсолютную величину
.

Полное ускорение точки A , или просто ускорение, равно векторной сумме касательного и нормального ускорений:
.
Поскольку векторы и перпендикулярны, то абсолютная величина ускорения точки A определяется по формуле:
.

Поступательное прямолинейное движение

Теперь рассмотрим прямолинейное поступательное движение тела. Направим ось x вдоль его линии движения. Пусть s есть перемещение тела вдоль этой оси относительно некоторого начального положения. Тогда скорость движения всех точек тела равна производной перемещения по времени:
.
При , вектор скорости направлен вдоль оси x . При – противоположно этой оси.

Ускорение точек тела равно производной скорости по времени, или второй производной перемещения по времени:
.
При , вектор ускорения направлен вдоль оси x . При – противоположно.

Соприкосновение тел без проскальзывания

Рассмотрим два тела, находящиеся в зацеплении без проскальзывания. Пусть точка A принадлежит первому телу, а точка B – второму. И пусть, в рассматриваемый момент времени, положения этих точек совпадают. Тогда, если между телами нет проскальзывания, то скорости этих точек равны:
.
Если каждое из тел вращается вокруг неподвижной оси, то равны соответствующие касательные ускорения:
.
Если одно из тел движется поступательно (пусть это второе тело), то ускорение его точек равно касательному ускорению точки соприкосновения первого тела:
.

Пример решения задачи

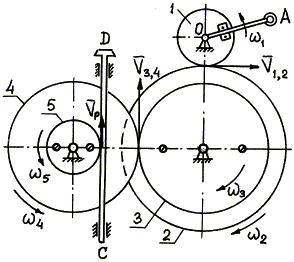
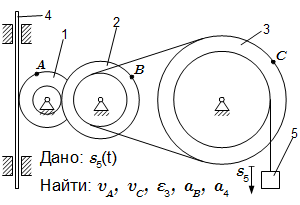
Механизм состоит из ступенчатых колес 1, 2, 3, находящихся в зацеплении и связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес. Радиусы ступеней колес равны соответственно: у колеса 1 – r₁ = 2 см, R₁ = 4 см, у колеса 2 – r₂ = 6 см, R₂ = 8 см, у колеса 3 – r₃ = 12 см, R₃ = 16 см. На ободьях колес расположены точки A, B и C. Задан закон движения груза: s₅ = t 3 – 6t (см). Положительное направление для s₅ – вниз.

Определить в момент времени t = 2 скорости точек A, C; угловое ускорение колеса 3; ускорение точки B и ускорение рейки 4.

Указания. Эта задача – на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что проскальзывание в ременной передаче и в точках сцепления колес отсутствует. То есть скорости точек колес, находящихся в зацеплении равны, а скорости точек ремня равны скорости точек, лежащих на ободе колес, связанных ременной передачей.

Дано:
t = 2 с; r₁ = 2 см, R₁ = 4 см; r₂ = 6 см, R₂ = 8 см; r₃ = 12 см, R₃ = 16 см; s₅ = t 3 – 6t (см).

Определение скорости и ускорения груза 5

Груз 5 совершает поступательное движение. Поэтому скорости (и ускорения) всех его точек равны. В условии задачи задано смещение s груза относительно некоторого начального положения. Дифференцируя по времени t , находим зависимость скорости точек груза от времени:
.
Дифференцируя скорость груза по времени, находим зависимость ускорения груза от времени:
.

Находим скорость и ускорение груза в заданный момент времени :
см/с;
см/с 2 .

Определение угловых скоростей и ускорений колес

Груз 5 связан нитью с внутренним ободом колеса 3. Поэтому скорости точек внутреннего обода колеса 3 равны скорости груза:
.
Отсюда находим угловую скорость колеса 3 для произвольного момента времени:
.
Здесь подразумевается, что и являются функциями от времени t . Дифференцируя по t , находим угловое ускорение колеса 3:
.
Находим значения угловой скорости и углового ускорения в момент времени с. Для этого подставляем найденные значения и при с:
с –1 ;
с –2 .

Рассмотрим колесо 2. Его внутренний обод связан нитью с внешним ободом колеса 3. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 2 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Рассмотрим колесо 1. Его внутренний обод находится в зацеплении с внешним ободом колеса 2. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 1 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Итак, мы нашли:
ω ₁ = 5.3333 с –1 , ω ₂ = 1.3333 с –1 , ω ₃ = 0.5 с –1 , ε ₁ = 10.6667 с –2 , ε ₂ = 2.6667 с –2 , ε ₃ = 1 с –2 .

Определение скоростей точек A и C

Точка A лежит на окружности радиуса R₁ с центром в точке O₁, расположенной на оси вращения. Поэтому скорость этой точки направлена по касательной к окружности и по абсолютной величине равна
см/с.

Точка C лежит на окружности радиуса R₃ с центром O₃ на оси вращения. Скорость этой точки:
см/с.

Определение ускорения точки B

Точка B лежит на окружности радиуса R₂ с центром O₂, расположенном на оси вращения. Касательное (или тангенциальное) ускорение этой точки направлено по касательной к окружности в сторону, на которую указывает угловое ускорение (по часовой стрелке). По абсолютной величине оно равно
см/с 2 .

Нормальное ускорение всегда направлено к центру окружности. По абсолютной величине оно равно
см/с 2 .

Полное ускорение равно векторной сумме касательного и нормального ускорений:
.
Поскольку касательное ускорение перпендикулярно нормальному, то для абсолютной величины полного ускорения имеем:
см/с 2 .

Определение ускорения рейки 4

Рейка 4 движется поступательно по направляющим. Она находится в зацеплении с внешним ободом колеса 1. Поэтому ее скорость равна скорости точек внешнего обода колеса 1:
.
Дифференцирую по времени, получаем ускорение рейки в произвольный момент времени:
.
Подставляем численные значения для момента времени t = 2 с :
см/с 2 .

см/с; см/с; с –2 ; см/с 2 ; см/с 2 .

Автор: Олег Одинцов . Опубликовано: 25-10-2019