Движение точки по траектории описывается уравнением

Уравнение движения материальной точки

Движение материальной точки в пространстве – это изменение ее положения относительно других тел с течением времени.

Имеет смысл говорить только о движении в некоторой системе отсчета.

Система отсчета. Системы координат

Точки, располагаемые в пустом пространстве, не различаются. Поэтому о точке рассуждают при условии нахождения в ней материальной точки. Определить ее положение можно при помощи измерений в системе координат, где и проводится нахождение пространственных координат. Если рассматривать в виде примера поверхность Земли, то следует учитывать широту и долготу располагаемой точки.

В теории используется декартова прямоугольная система координат, где определение точки возможно при наличии радиус-вектора r и трех проекций x , y , z – ее координат. Могут быть применены другие:

• сферическая система с положением точек и ее радиус-вектором, определенных координатами r , υ , φ ;
• цилиндрическая система с координатами p , z , α ;
• на полярной плоскости с параметрами r , φ .

В теории зачастую не принимают во внимание реальную систему отсчета, а сохраняют только ту, которая представляет собой ее математическую модель, применяемую во время практических измерений.

Кинематическое уравнение движения материальной точки

Любая система отсчета или координат предполагает определение координат материальной точки в любой момент времени.

При условии положения и определения материальной точки в данной системе отсчета считается, что ее движение задано или описано.

Это возможно при использовании кинематического уравнения движения:

Аналитически положение точки определяется совокупностью трех независимых между собой чисел. Иначе говоря, свободная точка имеет три степени свободы движения.

Ее перемещение по уравнению ( 1 ) определено, если имеется указанное положение в любой момент времени t . Для этого следует задавать декартовы координаты точки в качестве однозначных и непрерывных функций времени:

x ( t ) = x , y ( t ) = y , z ( t ) = z ( 2 ) .

Прямоугольные декартовы координаты x , y , z — это проекции радиус-вектора r ¯ , проведенного из начала координат. Очевидно, что длину и направление r ¯ можно найти из соотношений, где a , β , γ являются образованными радиус-вектором углами с координатными осями.

Равенства ( 2 ) считают кинематическими уравнениями движения материальной точки в декартовых координатах.

Они могут быть записаны в другой системе координат, которая связана с декартовой взаимно однозначным преобразованием. Если движение точки происходит в плоскости О х у , тогда применимы полярные координаты r , φ , относящиеся к декартовым преобразованиям. Данный случай подразумевает использование уравнения движения точки следующего вида:

r = r ( t ) , φ = φ ( t ) ( 3 ) .

Кинематическое уравнение движения точки в криволинейных координатах q 1 , q 2 , q 3 , связанных с декартовыми преобразованиями вида x = x ( q 1 , q 2 , q 3 ) , y = y ( q 1 , q 2 , q 3 ) , z = z ( q 1 , q 2 , q 3 ) ( 4 ) , записывается как

q 1 = q 1 ( t ) , q 2 = q 2 ( t ) , q 3 = q 3 ( t ) ( 5 ) .

Кривая радиус-вектора, описываемая концом вектора r при движении точки, совпадает с ее траекторией. Параметрическое уравнение траектории с t представлено кинематическими уравнениями ( 2 ) , ( 5 ) . Чтобы получить координатное уравнение траектории следует исключить время из кинематических уравнений.

Определение движения точки возможно с помощью задания траектории и мгновенного положения точки на ней. Ее положение на кривой определяется с помощью указания только одной величины: расстояния вдоль кривой от некоторой начальной точки с положительным направлением:

Это и есть уравнение движения точки по траектории. Способ его задания относят к естественному или траекторному.

Понятия координатного и естественного способа задания движения точки физически эквивалентны. С математической стороны это рассматривают как возможность применения разных методов, исходя из случая математической задачи.

Задание такого закона возможно аналитическим, графическим путем или с использованием таблицы, последние два из которых зачастую рассматривают в виде графиков и расписаний движений поездов.

Дано уравнение движения материальной точки x = 0 , 4 t 2 . Произвести запись формулы зависимости υ x ( t ) , построить график зависимости скорости от времени. На графике отметить площадь, численно равную пути, пройденному точкой за 4 секунды, произвести вычисление.

Дано: x = 0 , 4 t 2 , t = 4 c

Найти: υ x ( t ) , S — ?

Решение

При решении необходимо учитывать зависимость скорости от времени:

υ x = υ 0 x + a x t .

Зависимость координаты от времени и сравнение уравнения с заданным принимает вид:

x = x 0 + υ 0 x t + a x t 2 2 , x = 0 , 4 t 2 .

Очевидно, что x 0 = 0 , υ 0 x = 0 , a x = 0 , 8 м / с 2 .

После подстановки данных в уравнение:

Определим точки, изобразим график:

υ x = 0 , t = 0 , υ x = 4 , t = 5

Путь, по которому двигалось тело, равняется площади фигуры, ограниченной графиком, и находится с помощью формулы:

Траектория и уравнения движения точки

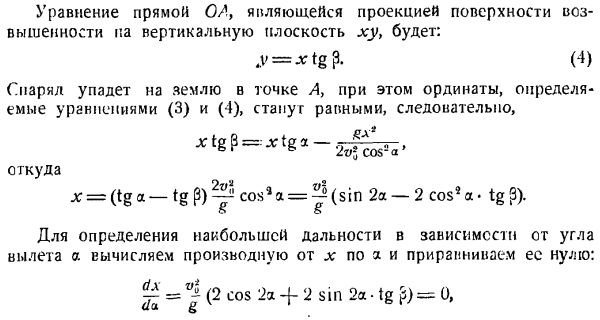
Траектория и уравнения движения точки

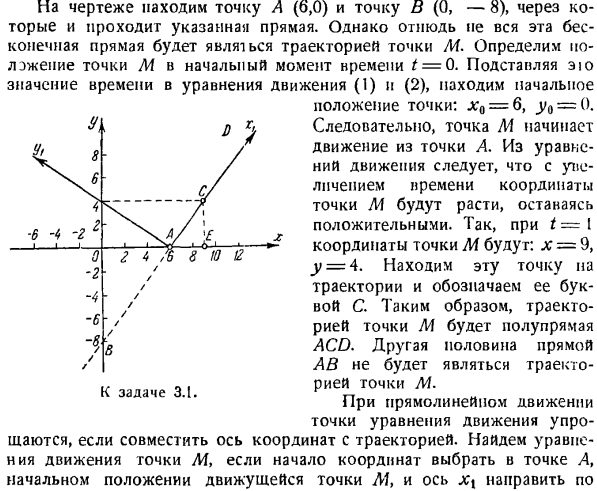
• Уравнение движения для локуса и точек 1°.Основные понятия. Траекторией точки называется линия, описываемая точкой движения в пространстве. Траектории могут быть плоскими или пространственными кривыми. Движение точки определяется установлением закона движения. Закон движения точек (уравнения) устанавливает зависимость расположения точек во временном пространстве.

Движение точки M в фиксированной системе координат xyz определяется установкой 3 функций (рис.3.1). * = / > ( ’). J’ = / *( Людмила Фирмаль

Создайте уравнение движения для точки N в декартовой системе координат. Найдите уравнение его орбиты. Определяет полный 1-кратный поворот точки N и точку, в которой координаты обеих точек равны. The solution. To составьте уравнение движения точки N, необходимо представить ее координаты в виде функции времени. Из рисунка найдите координату x в точке N. Х = О с COS Людмила Фирмаль

Затем по координатам определяется максимальное отклонение точки м от центра колебаний О. МПМ = а ХІ =-а. Величина a называется амплитудой колебаний, kt — (- (J называется фазой колебаний, ap-начальной фазой колебаний. Определите период колебаний, то есть время, в течение которого точки совершают 1 полное колебание, то есть возвращаются в исходное положение с той же скоростью и величиной. Обозначим период буквой Т и найдем его значение из условия, что приращение фазы колебаний за это время равно 2π. Иначе говоря

Задача 3.4.Точки перемещаются в соответствии с уравнением. x = A cos(kt-e), (1） г = Б, потому что КТ(2） Определите уравнение траектории движения точки. Как изменяется локус точек при увеличении разности фаз£от 0 до 2r? The solution. To найдя уравнение орбиты точки в явном виде, нужно исключить время из уравнения motion. To для этого сначала преобразуем уравнение движения. х = а соѕ(т-е)= а [потому что КТ потому что£-(- КТ грех грех ЭЖ.(3） решая уравнения (2) и (3) для cos kt и sin kt, получим: Х г — г соз£ а б. Преступление. потому что КТ =£о грех КТ = Добавьте эти уравнения, возведя их в квадрат. г, (т -£»»’) ’ 1 Б% ’ °1 (4） Sin2 е

Или в конце： — В + М — ^^ ко ^ грех ’、 уравнение (4) для любого значения e является уравнением эллипса. Из этого уравнения максимальные и минимальные значения являются Параметры±соответственно. a для x и zt b для y. таким образом, во всех случаях эллипс вписывается в прямоугольники со сторонами 2a и 2b. измените значение от 0 до 2ir. если e = 0, то выражение(4) принимает вид:

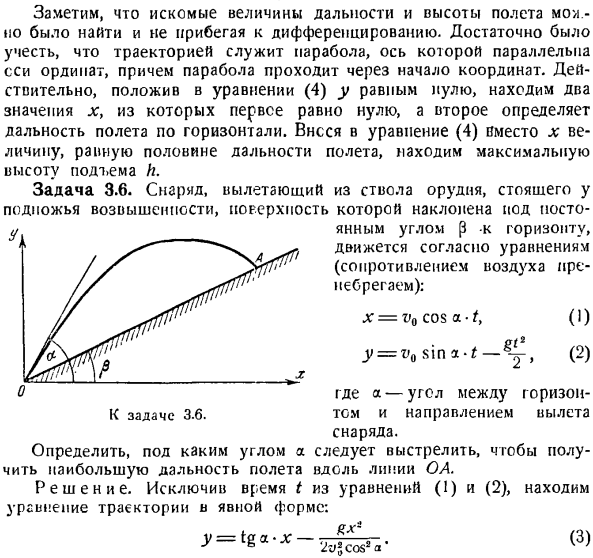
Так, если фазы обеих составляющих колебаний перпендикулярны друг другу, то эллипс вырождается в 2 совпадающие прямые, являющиеся диагоналями прямоугольника(рис. в коса -> -= учитывая it_y = 0, горизонтальная дальность полета I определяется из орбитального уравнения (4).

log A x cos2 a следовательно 2 значения x\ Т / л грех 2а х0 = 0, ХН = 1 = 8. Первое значение соответствует первому моменту (моменту отправления точки), А второе определяет горизонтальное расстояние. Сравнивая значения /и 5, можно сделать вывод, что/ = 2s, то есть точки достигают наивысшего положения в диапазоне горизонтальной половины. Итак, положение точки в пространстве в этой точке.

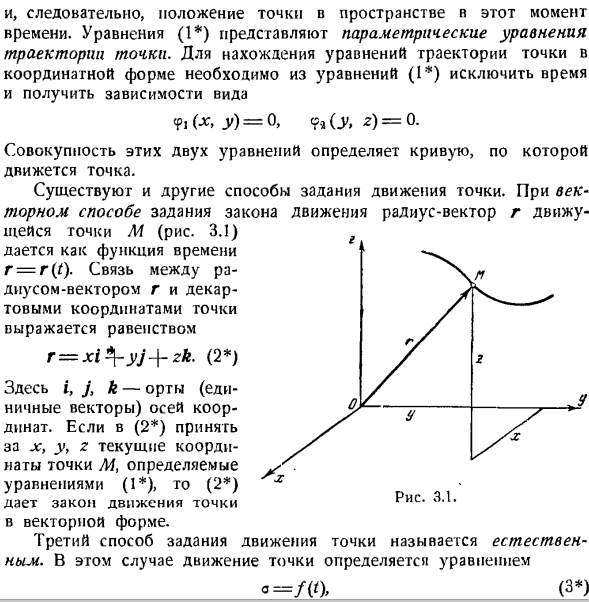
Уравнение (1) представляет собой параметрическое уравнение траектории a point. To найдя уравнение орбиты точки в координатной форме, нужно исключить время из уравнения(1) и получить форму зависимости. БФ,(Ци, г)= 0, 9а, КР, з)= 0. Комбинация этих 2 уравнений определяет кривую, по которой перемещаются точки. Есть и другие способы указать движение points. In векторным методом, определяющим законы движения, радиус-вектор r движущейся точки M (рис.3.1) задается как функция времени r = r (t).Связь между радиус-вектором r и Декартовыми координатами точки представлена уравнением Р = ХІ * \ — ый + ЗК. (2 ） Где i, j и k-единичные векторы (единичные векторы) осей. (2)

Если вы получаете x, y> z, текущие координаты точки A4, как определено y. уравнение(1), то (2) x Дайте закон движения точек в векторной форме. 3-й способ задания движения точек называется natural. In в этом случае движение точек определяется уравнением а = /( (). Сферические и цилиндрические координаты часто используются для изучения движения точки в пространстве. Сферическими координатами точки M (рис.3.4) являются расстояние r точки M от неподвижного центра O, угол φ (угол поворота плоскости zOM относительно неподвижной плоскости xOz) и угол ？ =?(’) * (5 *）

Уравнение движения для цилиндрических координат： р = п(о> т = м р = РЗ). (си *） м г Так… 1. Рисунок 3.4. Да. Чтобы перейти от сферических координат к декартовым, используйте следующую формулу:> х = р с с COS

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

КИНЕМА́ТИКА

КИНЕМА́ТИКА (от греч. ϰίνημα , род. п. ϰινήματος – дви­же­ние), раз­дел ме­ха­ни­ки , в ко­то­ром опи­сы­ва­ют­ся гео­мет­рич. ха­рак­те­ри­сти­ки дви­же­ния ме­ха­ни­че­ско­го – дви­же­ния ма­те­ри­аль­ных то­чек и их сис­тем, аб­со­лют­но твёр­дых тел и т. д. Со­от­вет­ст­вен­но вы­де­ля­ют раз­де­лы К.: К. ма­те­ри­аль­ной точ­ки, К. сис­те­мы то­чек, К. твёр­до­го те­ла и т. д.