Единственность решения для уравнения лапласа

Ответы на билеты

Уравнение Пуассона и Лапласа. Теорема единственности решения

Расчет электростатических полей с использованием уравнений и возможен только в простейших случаях. Наиболее общим методом является расчет электростатических полей на основе решения уравнений Пуассона и Лапласа. Выведем эти уравнения.

Ранее было получено . Подставим это выражение в уравнение дивергенции:

или ― уравнение Пуассона.

Уравнение Пуассона справедливо для тех точек среды, где существуют объемные заряды .

В реальных условиях свободные заряды располагаются на поверхности проводников бесконечно тонким слоем. Объемная плотность таких зарядов равна бесконечности и уравнение Пуассона применительно к ним теряет свой смысл.

В диэлектриках, которыми разделены заряженные проводники, объемные заряды отсутствуют ( ), уравнение Пуассона превращается в уравнение Лапласа:

или ― уравнение Лапласа.

Таким образом, электростатическое поле в диэлектрике описывается уравнением Лапласа, внутри проводников поле отсутствует вообще, а на границе раздела диэлектрика с проводником вступают в силу граничные условия , .

В декартовой системе координат операцию двойного дифференцирования записывают так:

Уравнение Лапласа в электростатике имеет исключительно важное значение.

Уравнения Пуассона и Лапласа, как уравнения в частных производных, допускают множество линейно независимых частных решений. Однако в реальных условиях каждой конкретной задаче соответствует только одно определенное решение.

Теорема единственности решения гласит, что найденное любым способом решение уравнений Пуассона или Лапласа, является единственно верным решением, если оно удовлетворяет граничным условиям данной задачи.

Предположим, что существует два решения для вектора напряженности поля и , оба удовлетворяющие граничным условиям задачи. Тогда получим:

Если rot и div от вектора равны нулю, то сам вектор тождественно равен нулю, следовательно , или , что требовалось доказать.

Из теоремы единственности решения вытекают два следствия, имеющее важное практическое значение:

электростатическое поле в некотором объеме, ограниченном эквипотенциальной поверхностью, не изменится, если эту поверхность заменить бесконечно тонким проводящим слоем;

электростатическое поле по одну сторону некоторой поверхности S не изменится, если по другую сторону поверхности изменить параметры среды (например, заменить поводящую среду диэлектриком) и изменить расположение свободных зарядов так, чтобы на этой поверхности сохранились прежние граничные условия.

Второе следствие лежит в основе так называемого метода зеркальных отображений, применяемого на практике для расчета электростатических полей.

Лекция 8. Принцип максимума для гармонических функций

Среди свойств, которыми обладают гармонические функции, одно свойство, называемое принципом максимума, несомненно имеет ведущее значение.

Теорема. Если функция U=U(x,y) гармоническая в ограниченной области D и непрерывная в соответствующей замкнутой области то она не может внутри этой области принимать значения, большие чем максимум ее значений на границе Г, и меньшие, чем минимум ее значений на Г, то есть

Доказательство. Обозначим через m максимум значений U(x,y) на Г и предположим, что максимальное значение функции равно U(x_o,y_o)=M>m и принимается во внутренней точке (x_o , y_o) области D. Составим вспомогательную функцию

где d — диаметр области D (максимальное расстояние между любыми двумя точками, принадлежащими области). Из неравенства вытекает, что на Г

В то же время функция V(x,y) принимает свое максимальное значение в некоторой (внутренней) точке области D, причем

Как известно, в этой точке V_x = V_y = 0, а следовательно, Однако

Полученное противоречие означает, что предположение M > m неверно, и мы доказали, что внутри D

Для доказательства неравенства, ограничивающего U(x, y) снизу

достаточно применить уже полученный результат к функции — U(x, y), которая, очевидно, тоже является гармонической. Теорема о максимуме и минимуме доказана.

На самом деле, если гармоническая функция , то она не может принимать внутри области D значения, равные и, то есть

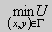
Это утверждение называется строгим принципом максимума (в отличие от предыдущего утверждения — «нестрогого» принципа максимума). Его доказательство сложнее, и мы доказывать это утверждение не будем. Сформулируем следствия из него.

Следствие 1. Если функция U=U(x, y) непрерывная в ограниченной замкнутой области и гармоническая в D, то

В частности, если , то U(x, y) ≡ 0 в D.

Это утверждение вытекает из (39):

Объединяя эти неравенства в систему, будем иметь:

Из принципа максимума следуют и многие другие важные свойства гармонических функций. Однако мы сейчас сформулируем и докажем лишь две теоремы.

Напомним постановку задачи Дирихле: в области D найти решение уравнения Лапласа, удовлетворяющее граничному условию U|_Г = f(s).

Теорема о единственности решения задачи Дирихле.

Решение задачи Дирихле для уравнения Лапласа в ограниченной области (если оно существует) единственное.

Доказательство. Пусть задача имеет два решения U=U₁(x, y) и U=U₂(x, y), удовлетворяющих одному и тому же условию Дирихле на границе Г. Тогда их разность V = U₁ — U₂ тоже будет непрерывной и гармонической функцией и на границе будет обращаться в нуль. По принципу максимума

Следовательно, V = U₁ — U₂ ≡ 0, то есть U₁(x, y) ≡ U₂(x, y). Единственность доказана. Вторая теорема имеет еще более длинное название.

Теорема о непрерывной зависимости решения задачи Дирихле от граничных условий.

Пусть U₁ и U₂ — две гармонические в области D функции, граничные значения которых равны, соответственно, f₁(s) и f₂(s), Если при некотором то всюду в рассматриваемой области D.

Доказательство. Рассмотрим функцию V = U₁ — U₂, удовлетворяющую уравнению Лапласа в области D и принимающую на границе Г значения f(s) = f₁(s)-f₂(s). На основании следствия 1 мы можем утверждать, что

что и требовалось доказать.

Эти теоремы имеют большое значение в вопросе о корректности задачи Дирихле, который мы рассмотрим в дальнейшем.

Отметим, что принцип максимума выполняется и для функций, гармонических в пространственных областях.