Егэ по математике 2015 уравнения

Тренировочные варианты «Школково». Основная волна. Реальные варианты ЕГЭ 2015

Миша живёт в доме, в котором всего один подъезд. При этом на каждом этаже по \(5\) квартир. Миша живет в квартире номер \(29\) . На каком этаже живёт Миша?

Количество полных этажей, которые расположены ниже Мишиного, есть округлённый в меньшую сторону результат деления \(29\) на \(5\) , следовательно, \(5\) этажей ниже, чем Мишин, тогда Миша живёт на \(6\) этаже.

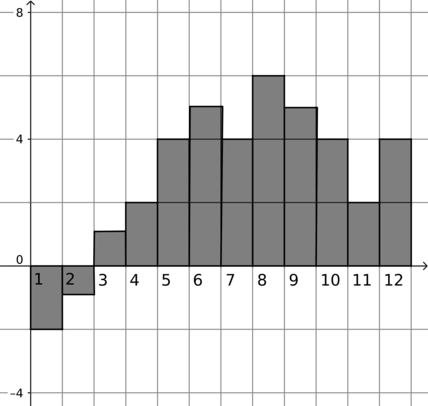
На диаграмме показана температура воздуха в Москве за первые \(12\) дней марта 2010 года. По горизонтали указываются дни месяца, по вертикали – температура в градусах Цельсия. Определите по диаграмме, сколько из указанных дней температура не превышала \(3\) градуса Цельсия.

Температура не превышала \(3\) градуса Цельсия \(1\) , \(2\) , \(3\) , \(4\) и \(11\) марта, то есть \(5\) дней.

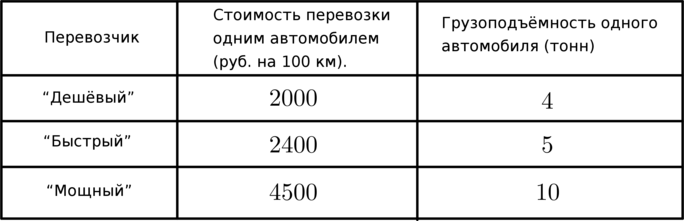
Для транспортировки \(38\ тонн\) груза на \(1000\ км\) можно комбинировать услуги трёх фирм-перевозчиков. Стоимость перевозки и грузоподъёмность автомобилей каждого перевозчика указаны в таблице.

Во сколько рублей обойдется наиболее дешёвый вариант перевозки?

Наиболее дешёвый способ: снарядить 3 машины перевозчика “Мощный” на \(1000\ км\) (то есть по 10 раз) и ещё 2 машины перевозчика “Дешёвый” на \(1000\ км\) , что обойдётся в \(3\cdot 4500\cdot 10 + 2\cdot 2000\cdot 10 = 175\,000\ руб\) .

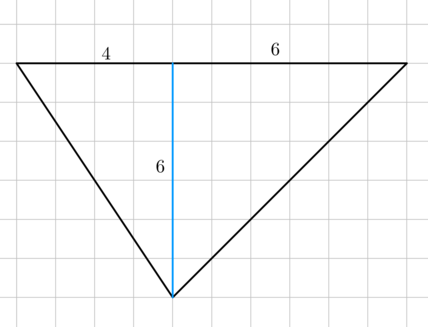
На клетчатой бумаге с размером клетки \(1\times 1\) изображён треугольник. Найдите его площадь.

Данный треугольник можно разрезать на два прямоугольных треугольника, как показано на рисунке. Площади полученных при этом треугольников будут равны \(0,5\cdot 4\cdot 6 = 12\) и \(0,5\cdot 6\cdot 6 = 18\) , следовательно, площадь исходного треугольника равна \(12 + 18 = 30\) .

На чемпионате по стрельбе из лука выступают \(40\) спортсменов, среди них по \(8\) стрелков из Дании и Туниса. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что пятым будет выступать стрелок из Дании.

Искомая вероятность есть отношение количества спортсменов из Дании к общему количеству спортсменов и равна \[\dfrac<8> <40>= 0,2\,.\]

Найдите корень уравнения \[(3x + 4)^2 = (8 + 3x)^2\]

\[(3x + 4)^2 = (8 + 3x)^2\quad\Leftrightarrow\quad 9x^2 + 24x + 16 = 9x^2 + 48x + 64\quad\Leftrightarrow\quad x = -2\,.\]

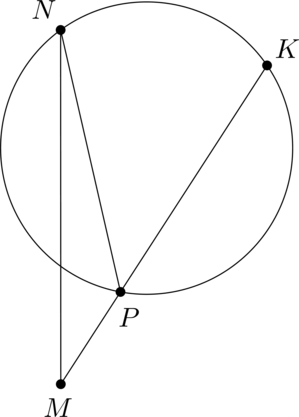
Угол \(NMK\) равен \(35^\circ\) , градусная мера дуги \(NK\) , не содержащей точку \(P\) , равна \(88^\circ\) . Найдите угол \(MNP\) . Ответ дайте в градусах.

Так как вписанный угол равен половине градусной меры дуги, на которую он опирается, то \(\angle NPK = 88^\circ : 2 = 44^\circ\) .

\(\angle NPK\) – внешний угол треугольника \(NMP\) , тогда \(\angle NPK = \angle NMK + \angle MNP\) , откуда \[\angle MNP = 44^\circ — 35^\circ = 9^\circ\,.\]

На рисунке изображён график \(y = f'(x)\) – производной функции \(f(x)\) , определённой на интервале \((-3; 19)\) . Найдите количество точек максимума функции \(f(x)\) , принадлежащих отрезку \([-1; 18]\) .

В точке максимума производная равна \(0\) , причём в некоторой окрестности точки максимума слева от неё производная должна быть положительна, а справа от неё – отрицательна. Таким образом, функция \(f(x)\) имеет единственную точку максимума на указанном отрезке ( \(x = 15\) ).

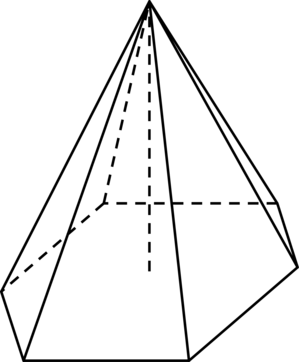
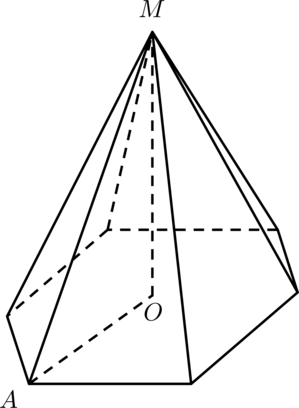
В правильной шестиугольной пирамиде боковое ребро равно \(13\) , а сторона основания равна \(5\) . Найдите высоту пирамиды.

В правильной пирамиде проекция \(O\) вершины \(M\) на плоскость основания есть центр описанной около основания окружности.

В правильном шестиугольнике расстояние от центра до вершины равно стороне, следовательно, \(AO = 5\) . Заметим, что \(\triangle MOA\) — прямоугольный, т.к. \(MO\) перпендикулярно плоскости основания. По теореме Пифагора \[MO^2 = MA^2 — AO^2\qquad\Rightarrow\qquad MO = \sqrt <13^2 - 5^2>= 12\,.\]

Найдите значение выражения \[\sqrt<8>\sin^2\dfrac<3\pi> <8>— \sqrt<2>\]

Используя формулу косинуса двойного угла \(\cos 2x = 1 — 2\sin^2 x\) , получаем \(\sin^2 x = \dfrac<1 - \cos 2x><2>\) , тогда \[\sqrt<8>\sin^2\dfrac<3\pi> <8>— \sqrt <2>= 2\sqrt<2>\cdot \dfrac<1 - \cos \dfrac<3\pi><4>> <2>— \sqrt <2>= 2\sqrt<2>\cdot \dfrac<1 + \dfrac<\sqrt2><2>> <2>— \sqrt <2>= \sqrt <2>+ 1 — \sqrt <2>= 1\,.\]

Известно, что при некотором физическом процессе, в котором участвует газ, выполнено соотношение \(p_1V_1^ <1,5>= p_2V_2^<1,5>\) , где \(p_1\) , \(p_2\) – давление газа в паскалях в начальный и конечный моменты времени, а \(V_1\) , \(V_2\) – объём газа в литрах в начальный и конечный моменты времени. В начальный момент времени объём газа равен \(3\ л\) , а его давление равно \(16\ атмосферам\) . Каким должен стать конечный объём газа, чтобы его конечное давление стало \(2\ атмосферы\) ? Ответ дайте в литрах.

Подставляя имеющиеся данные, получим \[16\cdot 3^ <1,5>= 2\cdot V_2^<1,5>\qquad\Rightarrow\qquad 2^3\cdot 3^ <1,5>= V_2^<1,5>\qquad\Rightarrow\qquad V_2 = 12\,.\]

В сосуд налили \(1500\ куб.\ см\) воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в \(1,4\) раза. Найдите объем детали. Ответ выразите в куб. см.

Объём жидкости с погружённой деталью стал \(1500\cdot 1,4 = 2100\ куб.см\) , следовательно, объём детали равен \(2100 — 1500 = 600\ куб.см\) .

Расстояние между городами \(M\) и \(N\) равно \(490\ км\) . Из города \(M\) в город \(N\) выехал первый автомобиль, а через час после этого навстречу ему из города \(N\) выехал второй автомобиль со скоростью \(80\ км/ч\) . Найдите скорость первого автомобиля, если автомобили встретились на расстоянии \(330\ км\) от города \(M\) . Ответ дайте в км/ч.

Расстояние, которое до места встречи проехал второй автомобиль, равно \(490 — 330 = 160\ км\) , следовательно, он ехал в течение \(160 : 80 = 2\ ч\) . Тогда первый автомобиль ехал до места встречи в течение \(2 + 1 = 3\ ч\) , следовательно, его скорость равна \(330 : 3 = 110\ км/ч\) .

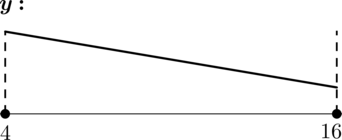
Найдите наименьшее значение функции \(y = \dfrac<2><3>x\sqrt — 4x + \dfrac<1><3>\) на отрезке \([4; 16]\)

ОДЗ: \(x \geqslant 0\) .

1) \[y’ = \dfrac<2><3>\left(\sqrt + \dfrac<2\sqrt>\right) — 4 = \sqrt — 4\] Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна \(0\) или не существует): \[y’ = 0\qquad\Leftrightarrow\qquad \sqrt = 4\qquad\Leftrightarrow\qquad x = 16\,.\]

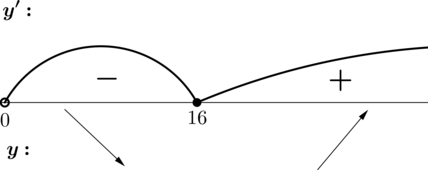
2) Найдём промежутки знакопостоянства \(y’\) :

3) Найдём промежутки знакопостоянства \(y’\) на отрезке \([4; 16]\) :

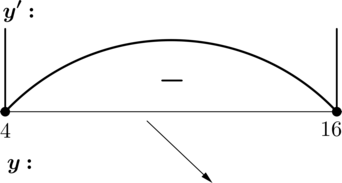
4) Эскиз графика \(y\) на отрезке \([4; 16]\) :

Таким образом, наименьшего значения на отрезке \([4; 16]\) функция \(y\) достигает в \(x = 16\) : \[y(16) = \dfrac<2><3>\cdot 64 — 64 + \dfrac<1> <3>= -21\,.\]

а) Решите уравнение \[\cos 2x + \sin \left(\dfrac<\pi> <2>— x\right) = 0\]

б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-2\pi; \dfrac<\pi><2>\right]\) .

а) ОДЗ: \(x\) – произвольный.

По формулам приведения и формуле косинуса двойного угла \(\cos 2x=2\cos^2x-1\) : \[2\cos^2 x — 1 + \cos x = 0\]

Сделаем замену \(\cos x = t\) : \[2t^2 — 1 + t = 0\qquad\Leftrightarrow\qquad 2(t — 0,5)(t + 1) = 0 \qquad\Leftrightarrow\qquad \left[ \begin \begin &t = -1\\ &t = 0,5 \end \end \right.\]

Сделаем обратную замену:

1) \(\cos x = -1\) равносильно \(x = \pi+2\pi n\) , \(n\in\mathbb\) .

2) \(\cos x = 0,5\) равносильно \(x = \pm \dfrac<\pi> <3>+ 2\pi k\) , \(k\in\mathbb\) .

б) \(-2\pi \leqslant \pi+2\pi n \leqslant \dfrac<\pi><2>\) равносильно \(-\dfrac32\leqslant n\leqslant -\dfrac<1><4>\) , но \(n\in\mathbb\) , следовательно, среди этих решений подходит только решение при \(n = -1\) : \(x = -\pi\) .

\(-2\pi \leqslant \dfrac<\pi> <3>+ 2\pi k_1 \leqslant \dfrac<\pi><2>\) равносильно \(-\dfrac<7> <6>\leqslant k_1 \leqslant \dfrac<1><12>\) , но \(k_1\in\mathbb\) , следовательно, среди этих решений подходят только решения при \(k_1 = -1\) и \(k_1=0\) : \(x = -\dfrac<5\pi><3>\) и \(x=\dfrac<\pi>3\) .

\(-2\pi \leqslant -\dfrac<\pi> <3>+ 2\pi k_2 \leqslant \dfrac<\pi><2>\) равносильно \(-\dfrac<5> <6>\leqslant k_2 \leqslant \dfrac<5><12>\) , но \(k_2\in\mathbb\) , следовательно, среди этих решений подходит только решение при \(k_2 = 0\) : \(x = -\dfrac<\pi><3>\) .

а) \(\pi+2\pi n,\ n\in\mathbb\) , \(\pm \dfrac<\pi> <3>+ 2\pi k,\ k\in\mathbb\)

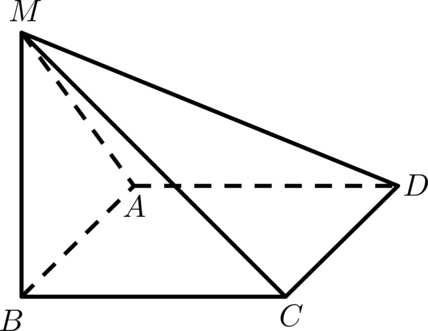
В основании четырёхугольной пирамиды \(MABCD\) лежит прямоугольник \(ABCD\) со сторонами \(AB = 4\) , \(AD = 15\) . При этом известны длины некоторых боковых рёбер: \(MA = \sqrt<26>\) , \(MB = \sqrt<10>\) , \(MC = \sqrt<235>\) .

а) Докажите, что \(MB\) – высота пирамиды \(MABCD\) .

б) Найдите угол между \(MD\) и плоскостью \((ABM)\) .

а) Рассмотрим треугольник \(MBA\) : \[MA^2 = 26 = 10 + 16 = (\sqrt<10>)^2 + 4^2 = MB^2 + BA^2\,,\] следовательно, треугольник \(MBA\) прямоугольный и \(MB\perp AB\) .

Рассмотрим треугольник \(MBC\) : \[MC^2 = 235 = 10 + 225 = (\sqrt<10>)^2 + 15^2 = MB^2 + BC^2\,,\] следовательно, треугольник \(MBC\) прямоугольный и \(MB\perp BC\) .

Таким образом, \(AB \perp MB\perp BC\) , то есть \(MB\) перпендикулярна двум пересекающимся прямым в плоскости \((ABCD)\) , следовательно, \(MB\) – высота пирамиды \(MABCD\) .

б) \[MB\perp (ABCD)\qquad\Rightarrow\qquad MB\perp AD;\qquad AB\perp AD\,,\] то есть \(AD\perp (MBA)\) , следовательно, \(AM\) – проекция \(MD\) на плоскость \((MAB)\) и угол между \(MD\) и \((MAB)\) равен углу \(AMD\) .

По теореме Пифагора в треугольнике \(MAD\) : \[MD^2 = MA^2 + AD^2 = 26 + 225 = 251\qquad\Rightarrow\qquad MD = \sqrt<251>\,.\] Тогда \[\sin AMD = \dfrac = \dfrac<15><\sqrt<251>>\qquad\Rightarrow\qquad \angle AMD = \arcsin \dfrac<15><\sqrt<251>>\,.\]

Решите неравенство \[1 -\dfrac<10> <3^— 1> + \dfrac<16> <(3^— 1)^2>\geqslant 0\]

ОДЗ: \[3^\neq 1\qquad\Leftrightarrow\qquad x^2 — 1\neq 0\qquad\Leftrightarrow\qquad x\neq \pm 1\]

Решим на ОДЗ. Сделаем замену \(t = 3^ — 1\) : \[1 — \dfrac<10>+ \dfrac<16>\geqslant 0\qquad\Leftrightarrow\qquad \dfrac\geqslant 0\qquad\Leftrightarrow\qquad \dfrac<(t - 2)(t - 8)>\geqslant 0\]

По методу интервалов

откуда \(t\in (-\infty; 0)\cup(0; 2]\cup[8; +\infty)\) . Таким образом, \[\left[ \begin 3^ — 1 что равносильно \[\left[ \begin x^2 Тогда с учётом ОДЗ ответ: \[x\in (-\infty; -\sqrt<3>]\cup[-\sqrt<2>; -1)\cup(-1; 1)\cup(1; \sqrt<2>]\cup[\sqrt<3>; +\infty)\,.\]

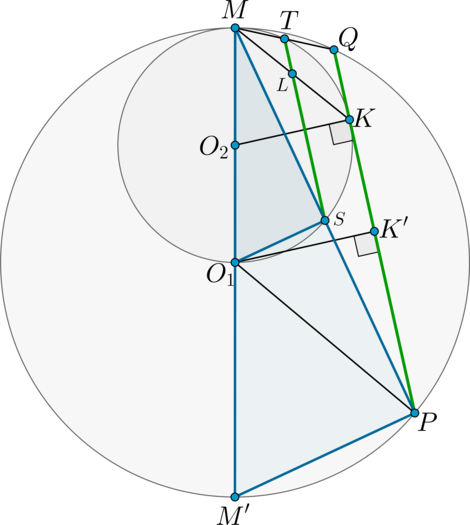
Две окружности касаются внутренним образом в точке \(M\) , причём меньшая из окружностей проходит через центр большей окружности. Хорда \(PQ\) большей окружности касается меньшей в точке \(K\) ; \(S\) и \(T\) – точки пересечения меньшей окружности с \(MP\) и \(MQ\) соответственно.

а) Докажите, что прямые \(ST\) и \(PQ\) параллельны.

б) Пусть \(L\) – точка пересечения \(MK\) и \(ST\) . Найдите \(ML\) , если радиус большей окружности равен \(5\) , а \(PQ = 6\) .

а) Пусть \(O_1\) и \(O_2\) центры большей и меньшей окружностей соответственно. Так как \(O_1M\) и \(O_2M\) перпендикулярны касательной, проходящей через точку \(M\) , то точки \(O_1\) , \(O_2\) и \(M\) лежат на одной прямой. Пусть \(M’\) – точка пересечения этой прямой с большей окружностью, отличная от \(M\) .

Докажем, что хорды данных окружностей, лежащие на одной прямой, проходящей через точку \(M\) , относятся как их диаметры. Рассмотрим доказательство на примере хорд \(MS\) и \(MP\) .

Рассмотрим треугольники \(MM’P\) и \(MO_1S\) . Эти треугольники прямоугольные, так как \(MO_1\) – диаметр меньшей окружности (описанной около треугольника \(MO_1S\) ), а \(MM’\) – диаметр большей окружности (описанной около треугольника \(MM’P\) ). При этом острый угол \(O_1MS\) у них общий, следовательно, эти треугольники подобны.

Из подобия получаем требуемое: \[\dfrac = \dfrac\]

Для других хорд, лежащих на прямой, проходящей через точку \(M\) , утверждение доказывается аналогично.

Из доказанного следует, что \[\dfrac = \dfrac\,.\]

Рассмотрим треугольники \(MST\) и \(MPQ\) : \(\angle SMQ\) – общий, \(\dfrac = \dfrac\) , следовательно, эти треугольники подобны, откуда \(\angle MST = \angle MPQ\) , следовательно, \(ST\parallel PQ\) .

б) Опустим перпендикуляры \(O_1K’\) и \(O_2K\) на \(PQ\) .

По теореме Пифагора \[K’O_1^2 = O_1P^2 — K’P^2\]

Так как \(O_1P = O_1Q\) , то \(O_1K’\) – медиана в треугольнике \(PO_1Q\) , следовательно, \(K’P = 3\) , тогда \(K’O_1 = \sqrt <25 - 9>= 4\) .

Так как \(MO_1\) – радиус большей окружности и диаметр меньшей, то радиус меньшей окружности равен \(0,5\cdot 5 = 2,5\)

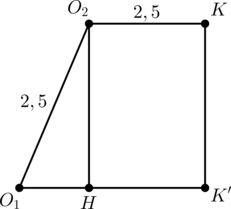
Рассмотрим прямоугольную трапецию \(O_2O_1K’K\) .

Пусть \(O_2H\) перпендикуляр к \(O_1K’\) , тогда \(O_1H = O_1K’ — O_2K = 4-2,5=1,5\) , следовательно, по теореме Пифагора \(2 = O_2H = KK’\) . Тогда \[PK = PK’+K’K=3+2=5,\qquad KQ = PK’-K’K=3-2=1.\]

Так как хорды данных окружностей, лежащие на одной прямой, проходящей через точку \(M\) , относятся как их диаметры, то \(ST\) – средняя линия в треугольнике \(MPQ\) , тогда \(SL\) – средняя линия в треугольнике \(MPK\) и \(LT\) – средняя линия в треугольнике \(MKQ\) , следовательно, \[SL = 0,5PK=2,5,\qquad LT = 0,5KQ=0,5\,.\]

По теореме о произведении отрезков хорд \[ML\cdot LK = SL\cdot LT = 1,25=\dfrac54\,,\] откуда, с учётом равенства \(ML = LK\) , получим \[ML = \dfrac<\sqrt<5>><2>\,.\]

15 января планируется взять кредит в банке на 11 месяцев. Условия его возврата таковы:

\(\bullet\) 1-ого числа каждого месяца долг возрастает на \(y\%\) по сравнению с долгом на конец предыдущего месяца;
\(\bullet\) со 2-ого по 14-ое числа каждого месяца необходимо выплатить часть долга в виде платежа банку;
\(\bullet\) 15-ого числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-ое число предыдущего месяца.

Известно, что общая сумма выплат по кредиту превысила сумму кредита на \(30\%\) процентов. Найдите \(y\) .

Фраза “долг должен быть на одну и ту же сумму меньше” означает, что кредит выплачивается дифференцированными платежами. Следовательно, т.к. кредит взят на 11 месяцев, то эта “одна и та же сумма”, на которую уменьшается долг каждый месяц, равна \(\frac1<11>\) части от суммы кредита. Обозначим сумму кредита за \(A\) и составим таблицу.
Т.к. каждый месяц долг увеличивается на \(y\%\) , то в первый месяц долг увеличиться на \(0,01y\cdot A\) рублей, то есть составит \(A+0,01yA\) рублей.
После выплаты долг должен уменьшиться на \(\frac1<11>A\) рублей, то есть должен составить \(\frac<10><11>A\) рублей. Значит, выплата в первый месяц будет равна \(A+0,01yA-\frac<10><11>A=0,01yA+\frac1<11>A\)

\[\begin <|l|c|c|c|>\hline \text<Номер месяца>&\text<Долг после начисления >\%& \text<Долг после выплаты>&\text<Выплата>\\ \hline 1& A+0,01y\cdot A& \frac<10><11>A& 0,01y\cdot A+\frac1<11>A\\ \hline 2& \frac<10><11>A+0,01y\cdot \frac<10><11>A& \frac<9><11>A& 0,01y\cdot \frac<10><11>A+\frac1<11>A\\ \hline 3& \frac9<11>A+0,01y\cdot \frac9<11>A& \frac8<11>A& 0,01y\cdot \frac9<11>A+\frac1<11>A\\ \hline \dots&\dots&\dots&\dots\\ \hline 10& \frac2<11>A+0,01y\cdot \frac2<11>A& \frac1<11>A& 0,01y\cdot \frac2<11>A+\frac1<11>A\\ \hline 11& \frac1<11>A+0,01y\cdot \frac1<11>A& 0& 0,01y\cdot \frac1<11>A+\frac1<11>A\\ \hline \end\]

Заметим, что все выплаты состоят из двух частей, причем одна часть \(\left(\frac1<11>A\right)\) фиксирована.

По условию общая сумма выплат \(R\) превысила на \(30\%\) сумму кредита \(A\) . Это значит, что переплата по кредиту \(R-A\) составляет \(30\%\) от \(A\) . Найдем общую сумму выплат:

\(R=\left(0,01y\cdot A+\frac1<11>A\right)+\left(0,01y\cdot \frac<10><11>A+\frac1<11>A\right)+ \left(0,01y\cdot \frac9<11>A+\frac1<11>A\right)+\dots+\)

\(+\left(0,01y\cdot \frac2<11>A+\frac1<11>A\right)+\left(0,01y\cdot \frac1<11>A+\frac1<11>A\right)=\)

\(=0,01y\cdot A\left(1+\frac<10><11>+\frac9<11>+\dots+\frac2<11>+\frac1<11>\right)+11\cdot \frac1<11>A=\)

В скобке — сумма 11 членов арифметической прогрессии, где \(a_1=\frac1<11>, \ a_<11>=1\) . По формуле \(S_<11>=\dfrac>2\cdot 11\) , значит

\(=0,01y\cdot A\cdot \frac12\left(\frac1<11>+1\right)\cdot 11+A=0,06yA+A\)

Тогда переплата составила \(R-A=0,06yA\) . Т.к. переплата составила \(30\%\) от \(A\) , то

Найдите все значения параметра \(a\) , при каждом из которых система уравнений

\[\begin x^2 — 4x + y^2 + 2y + 3,75 = |4x — 2y — 10|\\ 2x + 4y = a \end\]

имеет более двух решений.

Рассмотрим два случая:

1) \(4x — 2y — 10\geqslant 0\)
Первое уравнение системы в этом случае приводится к виду \[x^2 — 8x + y^2 + 4y + 13,75 = 0\qquad\Leftrightarrow\qquad (x — 4)^2 + (y + 2)^2 = 2,5^2\,.\]

Отдельно рассматриваемое данное уравнение задаёт на плоскости \((x; y)\) окружность с центром в точке \(O_1(4; -2)\) и радиусом \(2,5\) , но с учётом условия \(4x — 2y — 10\geqslant 0\) нам подходит только часть этой окружности, лежащая в полуплоскости \(y \leqslant 2x — 5\) .

2) \(4x — 2y — 10
Первое уравнение системы в этом случае приводится к виду \[x^2 + y^2 = 6,25\qquad\Leftrightarrow\qquad x^2 + y^2 = 2,5^2\,.\]

Отдельно рассматриваемое данное уравнение задаёт на плоскости \((x; y)\) окружность с центром в точке \(O(0; 0)\) и радиусом \(2,5\) , но с учётом условия \(4x — 2y — 10 нам подходит только часть этой окружности, лежащая в полуплоскости \(y > 2x — 5\) .

Решая системы уравнений \[\begin (x — 4)^2 + (y + 2)^2 = 2,5^2\\ y = 2x — 5 \end \qquad \text<и>\qquad \begin x^2 + y^2 = 2,5^2\\ y = 2x — 5 \end\,,\] находим, что окружности из пунктов 1) и 2) пересекаются с прямой \(y = 2x — 5\) в точках \(C(2,5; 0)\) и \(D(1,5; -2)\) .

При каждом фиксированном значении \(a\) второе уравнение исходной системы задаёт прямую, параллельную \(OO_1\) (при \(a = 0\) оно задаёт прямую \(OO_1\) , а при \(a\neq 0\) прямую, полученную из \(OO_1\) параллельным переносом).

Найдём значение \(a\) , при котором прямая \(y = 0,25a — 0,5x\) имеет с окружностью \(x^2 + y^2 = 2,5^2\) одну общую точку: \[x^2 + (0,25a — 0,5x)^2 = 2,5^2\qquad\Leftrightarrow\qquad 5(x^2 -0,2ax + 0,01a^2) + \dfrac <4>— \dfrac <20>= 25\,.\]

Чтобы данное уравнение имело единственное решение, необходимо и достаточно, чтобы левая часть представляла собой полный квадрат, откуда получим \(a^2 = 125\) , то есть \(a = \pm 5\sqrt<5>\) .

Проводя вычисления, можно показать, что при \(a = \pm 5\sqrt<5>\) окружность из пункта 2) также имеет с прямой \(y = 0,25a — 0,5x\) одну общую точку, то есть случаям \(\mathbf<1>\) и \(\mathbf<4>\) на рисунке отвечают прямые \(y = 0,25a — 0,5x\) при \(a = 5\sqrt<5>\) и \(a = -5\sqrt<5>\) соответственно.

Также легко показать, что случаям \(\mathbf<2>\) и \(\mathbf<3>\) отвечают прямые \(y = 0,25a — 0,5x\) при \(a = 5\) и \(a = -5\) соответственно.

Прямая \(y = 0,25a — 0,5x\) при \(a > 5\sqrt<5>\) не имеет общих точек с нарисованными дугами окружностей.
При \(a = 5\sqrt<5>\) эта прямая имеет две общие точки с этими дугами окружностей.
При \(5 эта прямая имеет четыре общие точки с этими дугами окружностей.
При \(a = 5\) эта прямая имеет три общие точки с этими дугами окружностей.
При \(-5 эта прямая имеет две общие точки с этими дугами окружностей.
При \(a = -5\) эта прямая имеет три общие точки с этими дугами окружностей.
При \(-5\sqrt <5>эта прямая имеет четыре общие точки с этими дугами окружностей.
При \(a = -5\sqrt<5>\) эта прямая имеет две общие точки с этими дугами окружностей.
При \(a эта прямая не имеет общих точек с этими дугами окружностей.

Таким образом, ответ: \[a\in (-5\sqrt<5>; -5]\cup[5; 5\sqrt<5>)\,.\]

Решение заданий егэ по математике 2015 уравнения

Презентация: «Решение заданий егэ по математике 2015 уравнения». Автор: Администратор. Файл: «Решение заданий егэ по математике 2015 уравнения.ppt». Размер zip-архива: 5794 КБ.

Решение заданий егэ по математике 2015 уравнения

Готов к ЕГЭ

Организатор вебинара: МОУ лицей №86

Ведущая вебинара: Никитина Светлана Васильевна, ведущий специалист

департамента образования мэрии города Ярославля; Выступление об особенностях ГИА 2015: Корнилова Ирина Вениаминовна, главный специалист департамента образования мэрии города Ярославля; Дистанционный урок математики проводят: Большакова Ольга Владимировна, директор МОУ лицея №86, учитель высшей категории ; Карпунина Елена Владимировна, учитель высшей категории МОУ лицея №86. Техническую поддержку осуществляет: Ткаченко Галина Владимировна, учитель информатики МОУ лицея №86.

ЕГЭ-2015, математика

Содержит задания, которые необходимы, чтобы использовать математический аппарат в повседневной жизни: проводить простейшие расчеты, оценку и прикидку; логически рассуждать; действовать в соответствии с несложными алгоритмами; использовать для решения задач учебную и справочную информацию; решать в том числе сложные задачи, требующие логических рассуждений.

Создан на основе экзаменационной модели ЕГЭ-2014 и проверяет: умения выполнять вычисления и преобразования; решать уравнения и неравенства; выполнять действия с функциями, с геометрическими фигурами; строить и исследовать математические модели.

ЕГЭ-2015, математика

Ориентирован на выпускника, у которого уровень знания математики неплохой, но дальнейшие планы связаны со специальностями, где математика не входит в перечень вступительных испытаний. Результаты базового ЕГЭ выдаются в отметках по пятибалльной шкале, не переводятся в стобалльную, не дают возможности участия в конкурсе на поступление в вузы, где требуются результаты ЕГЭ по математике.

Ориентирован на выпускника, для которого математика – один из вступительных экзаменов в вуз. Результаты оцениваются в стобалльной системе и могут быть представлены на конкурс для поступления в вуз, где математика является вступительным испытанием.

Апробация базового ЕГЭ

Участвовало 300 000 одиннадцатиклассников: 50% думают о поступлении в ВУЗ, где требуется ЕГЭ по математике; 40% считают предложенный вариант интересным; 20% считают предложенный вариант сложным. Не решили: 7 задач 10% участников; 10 задач 30% участников.

Апробация базового ЕГЭ

Апробация базового ЕГЭ

Апробация базового ЕГЭ

№	Слайд	Текст
1
10
11
12
13		Базовый уровень Одна часть из 20 заданий с кратким ответом базового уровня сложности Максимальный первичный балл – 20 Время выполнения работы – 3 часа Профильный уровень Часть 1 9 заданий с кратким числовым ответом Часть 2 (12 заданий) 5 заданий с кратким ответом 7 заданий с развернутым ответом Максимальный первичный балл – 34 Время выполнения работы – 3 часа 55 минут № Задания Проверяемые требования (умения) Уровень сложности задания Уметь решать уравнения и неравенства Уметь выполнять действия с геометрическими фигурами, координатами и векторами Уметь решать уравнения и неравенства Уметь выполнять действия с геометрическими фигурами, координатами и векторами Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни Уметь решать уравнения и неравенства Уметь строить и исследовать простейшие математические модели Необходимая теория Числовые множества Делимость Чётность Деление с остатком Каноническое разложение Взаимно простые числа Последовательности: арифметическая прогрессия, геометрическая прогрессия Метод «Оценка плюс пример» Демо-2015 На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно — 3 , среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно — 8 . а) Сколько чисел написано на доске? б) Каких чисел написано больше: положительных или отрицательных? в) Какое наибольшее количество положительных чисел может быть среди них? Решение а)Пусть среди написанных чисел а – количество положительных чисел; b – количество отрицательных чисел; с – количество нулей. Тогда количество всех написанных чисел равно а + b + с. Решение а)Пусть среди написанных чисел а – количество положительных чисел; b – количество отрицательных чисел; с – количество нулей. Тогда количество всех написанных чисел равно а + b + с, по условию задачи Решение а)Пусть среди написанных чисел а – количество положительных чисел; b – количество отрицательных чисел; с – количество нулей. Тогда количество всех написанных чисел равно а + b + с, по условию задачи 40 Решение заданий егэ по математике 2015 уравнения Егэ по математике 2015 уравнения ЕГЭ и ГИА по математике 2015 На этой странице публикуются материалы для подготовки к Единому государственному экзамену по математике 2015. Все представленные материалы получены из открытых источников и размещаются в ознакомительных целях. НИКАКИХ «РЕАЛЬНЫХ» КИМов, НИКАКИХ «ОТВЕТОВ» ДО ОКОНЧАНИЯ ЭКЗАМЕНОВ ЗДЕСЬ НЕТ, НЕ БЫЛО И НЕ БУДЕТ! Традиционно напоминаю: я не решаю никому никаких задач, ни за деньги, ни бесплатно, никаких «ответов» никуда не «скидываю». Обсуждения задач — на форуме. Генераторы вариантов ЕГЭ и ГИА База задач формируется на основе Открытого Банка, тренировочных и диагностических работ, пробных и реальных вариантов ЕГЭ и ГИА. Имеется возможность составить вариант в версии для печати. Тренировочные варианты ЕГЭ Тренировочные варианты составляются в соответствии с демовариантом и по спецификации ЕГЭ по математике 201 5 Варианты публикуются еженедельно: в воскресенье — вариант, в пятницу — ответы к нему. Есть возможность автоматической проверки 1-14 заданий варианта Образцы вариантов публикуются только ПОСЛЕ окончания экзамена в ознакомительных целях Диагностические и тренировочные работы МИОО в формате ЕГЭ — 2015 а также различные пробные варианты ЕГЭ Пробники:	Вариант 1-3	Вариант 4	Вариант 5 — 6	Вариант 7-8(б)	Вариант 9 — 12	Вариант 1 3	Вариант 1 4-15
Вариант 1 6	Вариант 1 7	Вариант 1 8	Вариант 1 9	Вариант 20	Вариант 21	Вариант 2 2

Апробация базового ЕГЭ 13-17 октября :

Варианты: 137751-54. 152741-44. 166081-84. 166211-14. 153691-94. 166701-04. 167691-94.

МИО O: Тексты вариантов диагностических работ МИОО не публикуются. Только обсуждения решений и видеоразборы.

18.09 Диагностическая 10 кл

23.09 Диагностическая 11 кл

21 .01 Диагностическая 11 кл

1 4 .05 Итоговая 10 кл база / пр

Дополнительные материалы для подготовки. Учебные пособия.

Все задания части С ЕГЭ 2014 С подробными официальными решениями.

Все задания части С ЕГЭ 2013 С подробными официальными решениями.

Все задания части С ЕГЭ 2012 С подробными официальными решениями.

Диагностические и тренировочные работы в формате ГИА — 2015

а также различные пробные варианты ГИА

Тренировочные варианты: Варианты публикуются еженедельно в среду, ответы — в понедельник.

МИОО : Тексты вариантов диагностических работ МИОО не публикуются. Только обсуждения решений и видеоразборы.

Литература для подготовки к ЕГЭ и ГИА 2015

Посмотреть эти и другие книги и сделать заказ можно здесь.