Экономическая задача по дифференциальным уравнениям

Задачи экономического содержания и дифференциальные уравнения, Монако Т.П., 2016

Задачи экономического содержания и дифференциальные уравнения, Монако Т.П., 2016.

Сборник задач предназначен для студентов высших учебных заведений. обучающихся по экономическим специальностям и изучающим математические дисциплины в соответствии с образовательными стандартами. Приведены разноуровневые экономические задачи, решение которых требует широкомасштабного использования аппарата дифференциальных уравнений. Представлен необходимый теоретический материал, позволяющий решать различные экономические проблемы методами дифференциальных уравнений. Некоторые параграфы содержат необходимый теоретический материал.
Данный задачник будет полезен студентам, аспирантам, преподавателям, а также все и всем желающим научиться применять математический инструментарий в экономических исследованиях и для успешного ведения бизнеса.

Уравнение инфляционного ожидания.
Согласно научным исследованиям на экономические процессы в условиях инфляции заметное влияние может оказывать настроение основной части населения относительно ожидаемого в будущем темпа роста цен. Так, если большая часть населения страны ожидает дальнейшего усиления роста цен, то она не станет вкладывать сбережения в банки, а будет покупать впрок товары повседневного спроса, менять деньги на твердую валюту. т.е. будет себя вести экономически разумно, и в результате темпы роста цен действительно будут увеличиваться.

Если же основная доля населения полагает, что в ближайшем будущем будет оживление в экономике и темпы инфляции снизятся, то люди будут больше покупать товаров длительного пользования и вкладывать деньги в банки (и, тем самым, инвестировать экономику страны), в результате. как правило, такое оживление в экономике действительно наступает.

Оглавление.
Предисловие.
§1. Задачи, приводящие к дифференциальным уравнениям.
1.1. Взаимосвязь функции спроса и эластичности.
1.2. Модель формирования равновесной цены на товар.
1.3. Модель естественного роста.
1.4. Задача об эффективности рекламы.
1.5. Уравнение инфляционного ожидания.
1.6. Задача о доходе и потреблении.
1.7. Закон логистического развития в инновационном менеджменте.
§2. Задачи экономического содержания, решаемые средствами дифференциальных уравнении.
ГЛОССАРИЙ.
Литература.

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Задачи экономического содержания и дифференциальные уравнения, Монако Т.П., 2016 — fileskachat.com, быстрое и бесплатное скачивание.

Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России. Купить эту книгу

Экономическая задача, приводящая к дифференциальному уравнению

Лекция 3-4

Обыкновенные дифференциальные уравнения

Общее и частные решения. Уравнения первого порядка. Уравнения с разделяющимися переменными. Однородные уравнения.

Линейные дифференциальные уравнения. Уравнение Бернулли.

Уравнений в полных дифференциалах.

Вопросы

1. Определение обыкновенных дифференциальных уравнений.

2. Дифференциальные уравнения первого порядка.

3. Общее решение дифференциального уравнения.

4. Задачи Коши. Частное решение.

5.Определение дифференциального уравнения 1-ого порядка.

6. Дифференциальные уравнения с разделяющимися переменными.

7. Однородные дифференциальные уравнения.

8. Линейные дифференциальные уравнения первого порядка.

10.Уравнение в полных дифференциалах

Различные вопросы экономики приводят к необходимости решения уравнений, содержащей в качестве неизвестной некоторую функцию и ее производные до определенного порядка n.

Экономическая задача, приводящая к дифференциальному уравнению

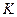
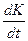
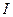
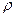
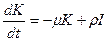
Обозначим — величина фондов в натуральном или стоимостном выражении. Фонды – это станки, помещения и т.п. они изнашиваются, стареют, как говорят, выбывают. Скорость выбытия фондов – это производная , она выражается через коэффициент выбытия . Например, если за 10 лет фонды полностью обновляются, то коэффициент выбытия равен =1/10. С другой стороны, инвестиции – вложение денег – ведут к увеличению фондов с коэффициентом пропорциональности . Учитывая все это, получим дифференциальное уравнение, вида:

.

Дата добавления: 2015-08-21 ; просмотров: 1124 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

ГЕОМЕТРИЧЕСКИЕ, ФИЗИЧЕСКИЕ И ЭКОНОМИЧЕСКИЕ ЗАДАЧИ, СВОДЯЩИЕСЯ К ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ

Надежда Шульга 5 лет назад Просмотров:

1 Министерство образования и науки Российской Федерации ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ Я.С. Гриншпон ГЕОМЕТРИЧЕСКИЕ, ФИЗИЧЕСКИЕ И ЭКОНОМИЧЕСКИЕ ЗАДАЧИ, СВОДЯЩИЕСЯ К ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ Учебное пособие Томск Издательство Томского государственного университета систем управления и радиоэлектроники

2 УДК 57.9, 5.7 ББК.6.6я73 Г85 Рецензенты: канд. физ.-мат. наук, проф. каф. высшей математики Томск. гос. ун-та систем упр. и радиоэлектроники А.А. Ельцов; канд. физ.-мат. наук, доц. каф. мат. анализа Томск. гос. ун-та Э.Н. Кривякова Г85 Гриншпон Я.С. Геометрические, физические и экономические задачи, сводящиеся к дифференциальным уравнениям: учеб. пособие / Я.С. Гриншпон. Томск: Изд-во Томск. гос. ун-та систем упр. и радиоэлектроники,. 74 с. ISBN Приведены геометрические, физические и экономические задачи, сводящиеся к обыкновенным дифференциальным уравнениям. Все задачи снабжены подробными решениями. Может использоваться как дополнительное учебное пособие при изучении дифференциальных уравнений в курсах высшей математики и математического анализа для технических и экономических специальностей вузов. УДК 57.9, 5.7 ББК.6.6я73 Учебное издание Гриншпон Яков Самуилович ГЕОМЕТРИЧЕСКИЕ, ФИЗИЧЕСКИЕ И ЭКОНОМИЧЕСКИЕ ЗАДАЧИ, СВОДЯЩИЕСЯ К ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ Учебное пособие Корректор Л.И. Кирпиченко Компьютерная верстка Я.С. Гриншпона Подписано в печать. Формат 6 84/6. Усл. печ. л. 4,4. Заказ. Тираж экз. Томский государственный университет систем управления и радиоэлектроники. 6345, г. Томск, пр. Ленина, 4. Тел. 8 (38) ISBN Гриншпон Я.С., Изд-во Томск. гос. ун-та систем упр. и радиоэлектроники,

3 Предисловие Многие студенты технических специальностей, проходящие курс высшей математики на младших курсах, высказывают мнение, что «математика это сухая теория, не имеющая практического значения». Конечно же, впоследствии, постоянно сталкиваясь с математическим аппаратом на специальных предметах, они изменят свое мнение. Но для лучшего усвоения материала и усиления заинтересованности в процессе обучения важно объяснить практическую ценность математических знаний именно в период их получения, т.е. на первом и втором курсах. Данное пособие призвано хотя бы частично помочь в решении поставленной проблемы. В нем рассматриваются достаточно простые прикладные задачи, сводящиеся к дифференциальным уравнениям. Отметим, что для решения всех предложенных задач не требуется никаких дополнительных знаний из области физики, геометрии или экономики, так как все необходимые сведения из этих областей приводятся в начале каждого параграфа. Однако так как данное пособие предназначено для использования в курсе высшей математики, то сведения из других наук не претендуют на полноту и общность и для более глубокого их изучения следует воспользоваться специализированной литературой по данным предметам. Пособие подготовлено с использованием работ [ ]. 3

4 Глава. Геометрические задачи.. Задачи на положение касательной Известно, что угловой коэффициент касательной, проведенной к графику функции y = f( x) в точке x, равен значению производной f ( x) в точке x. Другими словами, если y = kx+ b уравнение касательной, то. Так как, кроме того, касательная проходит k = f ( x ) = y через точку графика ( x; y ), где y = f( x), то получим: y = y ( x x ) + y уравнение касательной. Если y и y, то, полагая y =, а затем x =, найдем точки пересечения касательной с осями координат: y x ; точка пересечения касательной y с осью абсцисс, ( ; y y x) точка пересечения касательной с осью ординат. Если же y =, то уравнение касательной приобретает вид y = y это прямая, параллельная оси абсцисс и пересекающая ось ординат в точке (; ). А если y =, то y касательная задается уравнением x = x это прямая, параллельная оси ординат и пересекающая ось абсцисс в точке ( x;). Напомним также, что угловой коэффициент любой прямой, в частности касательной, равен тангенсу угла наклона этой прямой к положительному направлению оси абсцисс. При этом для возрастающей функции угол наклона касательной является внутренним для прямоугольного треугольника, образованного касательной и ординатой, про- 4

5 ходящими через точку ( x; y ), и осью абсцисс, поэтому BC y = tg α= (рис. ). А для убывающей функции он является AB внешним, и поэтому BC y = tg(8 α ) = AB (рис. ). у у C C С помощью касательной определяется понятие угла между двумя кривыми. Если графики двух дифференцируемых функций y = f( x) и y = g( x) пересекаются в точке с абсциссой x, то углом между этими кривыми называют наименьший угол между их касательными. Для тангенса k k этого угла верна формула tg γ=, где k и k уг- + kk ловые коэффициенты касательных, т.е. k k = f ( x ) α A B х B Рис. Рис. α A х = g ( x ). В частности, кривые будут перпендикулярными (tgγ = ), если kk =, где k и k отличны от нуля и бесконечности, или если одна из этих касательных горизонтальна, а другая вертикальна, т.е. k =, k = или, наоборот, k =, k =. Кривая, которая в каждой своей точке перпендикулярна некоторой линии семейства y = f( x, a), где параметр a принимает любые действительные значения, называется ортогональной траекторией к данному семейству. 5 и

6 Задача. Записать уравнения кривых, для которых площадь любого треугольника, образованного касательной и ординатой, проведенными из некоторой точки кривой, и осью абсцисс, равна единице. Начертить все непрерывные кривые, удовлетворяющие условию задачи и проходящие через точку (; ). Решение. Из чертежа (рис. 3) видно, у что искомый треугольник возникает только тогда, когда касательная не параллельна осям координат, т.е. y C и y. Запишем координаты вершин треугольника: A x ;, y B ( x ; ) и ( y C x; y), и вычислим длины катетов: AB = A B х y Рис. 3 y и BC = y. Следовательно, площадь треугольника AB BC y S ABC = =. y В силу произвольности выбора точки ( x; y ) можем записать дифференциальное уравнение y y =. Это уравнение с разделяющимися переменными. Рассмотрим два случая. Если y >, то y = y. Разделяя переменные, получим dx =, x= c и y dy y y = c x, что удовлетворяет рассматриваемому случаю, так как dy y = >. Если же y 7 x= c+ и y y = x c, причем y = , частные решения. x x Задача. Записать уравнения кривых, для которых точка пересечения любой касательной с осью абсцисс имеет абсциссу, отличающуюся в два раза от абсциссы точки касания. Начертить все непрерывные кривые, удовлетворяющие условию задачи и проходящие через точку ( ; ). Решение. Рассмотрим особые случаи, когда y = и y =. В первом случае касательная либо параллельна оси абсцисс, либо совпадает с ней, что не удовлетворяет условию задачи. Во втором случае абсциссы точки пересечения и точки касания равны. Следовательно, они могут отличаться в два раза только в том случае, когда x =. Имеем, что прямая x = является решением задачи. Пусть теперь y и y. Абсцисса точки пересечения касательной с осью абсцисс равна x. Считая y y 7

8 ( x; y ) произвольной точкой кривой, получим дифференциальные уравнения y y x = x или x x y =. y dy dx Преобразуем первое уравнение: y = y x, =, y x c c ln y = ln c ln x и y =. Так как производная y = x x не должна равняться нулю, то c (действительно, прямая y =, очевидно, не удовлетворяет условию задачи). dy dx Аналогично для второго уравнения: y = yx, =, y x ln y = ln c+ ln x и y = cx. Из условия y = cx следует, что c и начало координат не принадлежит искомым кривым, т.е. получаем семейство парабол с выколотой точкой (; ). Через точку ( ; ) проходят левые ветви параболы y = x и гиперболы y = (рис. 5). x у c Ответ: y = и y = cx, где x и x c, общее решение; x = особое х решение; y = x и y =, где, Рис. 5 x 9 Решение. В особом случае y = касательная либо не имеет точек пересечения с осью абсцисс, либо имеет бесконечно много точек пересечения, и задача не имеет смысла. Если же y =, то точка пересечения имеет координаты ( x;), а искомые расстояния равны y и x. Если потребовать равенства этих расстояний для любой точки кривой, т.е. y = x, или y =± x, то тогда y. Итак, особых решений нет. у Сделаем чертеж (рис. 6) и найдем ко- A A x ; y, ординаты точек: ( ) y B x ; и O(;). Из условия y AB = OB, верного для всех точек A( x ; y ), запишем уравнение y + y = x O B Рис. 6 y + y = x y, или y y y. Очевидными преобразованиями получаем однородное уравнение y =, которое заме- y y xy x y ной y = xu и y = u+ xu приводится к уравнению с разде- 3 x u u + u ляющимися переменными xu = u =. Заметим, что при сокращении на x мы не потеряли решение, x xu u так как выше было показано, что прямая x = не удовлетворяет условию задачи. х 9

10 dx u = 3 du Разделим переменные:. Проинтегрируем x u + u отдельно правую часть: u ( u ) u du + = du = uu ( + ) uu ( + ) = du u du ln u ln u ln c ln cu u = + + =. Значит, u + u + cu ln x = ln или x( u + ) =cu. Возвращаясь к перемен- u + y cy ной y, имеем x + =, или y + x = cy. x x Проверим условия неравенства производной нулю и бесконечности. Для этого продифференцируем общее решение yy + x = cy и выразим x y =. Видно, что c y y = при x =. Подставляя в общее решение, находим y = и y = c. А значит, точки (; ) и (; c) необходимо исключить из кривой. Далее, y = c c при y = и x =±, т.е. выполняется условие y =± x, и эти точки удовлетворяют условию задачи. Итак, решениями являются окружности y + x = cy с выколотыми точками (; ) и (; c). Через точку ( ; ) проходит левая половина окружности с центром в точке (; ) у единичного радиуса (рис. 7). Ответ: y + x = cy, где x, общее х решение; x = y y частное решение. Рис. 7

11 Задача 4. Записать уравнения кривых, для которых точка пересечения любой касательной с биссектрисой первого и третьего координатных углов имеет абсциссу, отличающуюся в два раза от абсциссы точки касания. Решение. В данной задаче особым будет являться случай y =. Действительно, в этом случае угловые коэффициенты касательной и биссектрисы первого и третьего координатных углов равны, а значит, эти прямые либо параллельны, либо совпадают. В случае же y = аналогично задаче имеем особое решение x =. Пусть теперь y и y. Координаты точки пересечения касательной y = y ( x x) + y с биссектрисой y yx y = x равны. Получаем дифференциальные уравнения = x или ( y yx ) = x. y y yx y y Преобразуем первое уравнение: y yx = x xy, или yx + y= x это линейное уравнение первого порядка. Соответствующее ему однородное уравнение yx + y= c имеет решение y =. Варьируя константу, получим x cx c c x + = x, и c = x c= x + c. Окончательно общее решение записывается в виде y = или y = x+. x x x + c c x x c Из условия y = следует, что c, т.е. прямая x y= x не является решением задачи. Аналогично для второго уравнения: y yx = x xy, yx y= x, y = cx решение однородного уравнения

12 + = yx y=. Решая методом вариации постоянной неодно- родное уравнение ( cx xc) x cx x, получим c =, c= + c и y = c x x cx + = +, где c. x x x c Ответ: y = x+ и y = x+ cx, где c, общее решение; x = особое x решение. Задача 5. Записать уравнения ортогональных траекторий к семейству эллипсов с центром в начале координат и осями, параллельными осям координат, причем одна из этих осей в два раза больше другой. Решение. В зависимости от того, какая из осей больше другой, уравнения эллипсов можно записать в виде x + 4y = R или 4x + y = R. Пусть ( x; y ) точка пересечения эллипса с ортогональной траекторией. Обратим внимание на то, что начало координат не принадлежит ни одному эллипсу из нашего семейства, а значит, x и y не могут одновременно равняться нулю. Продифференцировав в точке ( x; y ) уравнения эллипсов x + 8yy = или 8x + yy =, находим угловые x коэффициенты касательных к эллипсам k = y = или 4y 4x k = y =. Пусть теперь k это угловые коэффициенты ортогональных траекторий. y Рассмотрим особые случаи. Если k =, то x = и k =, а если k =, то y = и k =. Следовательно, прямые x = и y = с выколотой точкой (; ) представляют собой искомые ортогональные траектории.

13 Если же k и k, то для касательной к ортогональной траектории в любой точке этой траектории верно соотношение k =. Отсюда получаем дифференциальные уравнения y = или y =, решениями которых k 4y y x 4x 4 являются функции y = cx и y = c 4 x, где x. Заметим, что решение y = входит в полученные общие решения при c =. 4 Ответ: y = cx и y = c 4 x, где x, общее решение; x =, где y, особое решение. Задача 6. Записать уравнения кривых, образующих в каждой своей точке угол 45 с некоторой параболой из семейства y = ax. Решение. Пусть ( x; y) (;) точка пересечения искомой кривой с параболой y = ax. Тогда a = и y x y y k = y = ax = x =. Так как тангенс угла между x x кривыми равен единице, то, используя формулу k k y yy tg γ=, получаем уравнение ± y = +. + kk x x Уравнение y yy y = + является однородным. После замены y = ux и y = ux + u оно приобретет вид x x u ( ux + u) = + u( ux + u), или ux (u+ ) = u u. (u+ ) du dx Разделим переменные: =, и проинтегриру- u u+ x 3

14 u u,5 ем левую часть: + du = + du = u u+ u,5u+,5 u, 5,75 = du + du ( u,5) +, 4375 = ( u, 5) +, 4375 ln u,5u+,5,75 u,5 = + arctg + c =,4375,4375 ln u u+ 3 4u = + arctg + c. Следовательно, общее 7 7 c 3 4u решение имеет вид = u u+ exp arctg x, y x или c= y yx+ x exp arctg. При делении 7 7x на x мы не потеряли решение, так как прямая x = имеет только одну точку пересечения с любой параболой данного семейства. y yy Аналогично для уравнения y = + получаем x x (u ) du dx ux + u u= + u( ux + u), = и u + u+ x 3 4y+ x c= y + yx+ x exp arctg 7 7x. Заметим, что из области определения полученных кривых видно, что они не содержат начало координат, поэтому сделанное в начале решения допущение ( x; y) (;) правомерно. Также необходимо заметить, что в условии идет речь о параболах y = ax, а это означает, что параметр a подразумевается отличным от нуля. Следовательно, из решений выкалываются точки с нулевой ординатой. 4

15 3 x ± 4y Ответ: c= y ± yx+ x exp arctg 7 7x, где y, общее решение. Задача 7. Найти такие поверхности вращения, чтобы все лучи, исходящие из источника света, расположенного на оси вращения этой поверхности, отражались параллельно этой оси. Решение. Рассмотрим плоскую фигуру, вращением которой получается искомая поверхность, при этом источник света поместим в начало координат, а ось ординат направим по оси вращения. Выберем произвольную точку A( x ; y ) Рис. 8 на кривой и через B( ; y y x) обозначим точку пересечения касательной с осью ординат (рис. 8). Тогда OA x y = + и OB = y x y. Кроме того, так как отраженный луч параллелен оси ординат, то он с касательной образует тот же угол α, что и угол между касательной и осью ординат. Из оптики известно, что угол падения равен углу отражения, а значит, OAB = OBA и треугольник OAB равнобедренный, т.е. OA = OB. Получаем однородное уравнение y x y = x + y, или α B y+ x + y y =. Замена x y = ux приведет это уравнение к виду ux = + u, откуда du dx + u =, ln u+ + u = ln x + ln c, + u = xc u, x + u = x c xuc+ u, x c = + xuc. Возвращаясь к пе- у O α A х 5

16 cx ременной y, получим x c = + yc, или y = c это уравнение параболы. Записав это уравнение в каноническом виде x = y, видим, что параметр парабо- c c лы p =, а следовательно, ее фокус находится в начале c координат (из аналитической геометрии известно, что фокус находится на расстоянии = от вершины парабо- p c лы). Ответ: параболоиды вращения, у которых источник света находится в фокусе вращающейся параболы. Задачи на площадь криволинейной трапеции Напомним, что криволинейной трапецией называют плоскую фигуру, которая в декартовой системе координат ограничена осью абсцисс, прямыми x = a и x = b и графиком непрерывной функции y = f( x). Если a , то, зная площадь криволинейной трапеции, также можно вычислить координаты ( x ; y ) центра c 6 c a у Рис. 9 b x

17 тяжести этой трапеции: b yc f ( x) dx S a b x c b = xf ( x) dx S и =, где S = f( x) dx площадь трапеции. a Из указанных формул видно, что задачи, связанные с криволинейной трапецией, как правило, сводятся к интегральным уравнениям. Однако дифференцирование обеих частей уравнения и использование факта, что производная от интеграла с переменным верхним пределом равна подынтегральной функции, позволяет в большинстве случаев перейти от интегральных уравнений к дифференциальным. Задача 8. Записать уравнения кривых, обладающих следующим свойством: если через любую точку данной кривой провести прямые, параллельные осям координат, до пересечения с этими осями, то площадь полученного прямоугольника делится кривой в отношении :3. Начертить все непрерывные кривые, удовлетворяющие условию задачи и проходящие через точку (; ). A x ; y на кривой. Условие Решение. Выберем точку ( ) задачи подразумевает, что x и y отличны от нуля и что дуга искомой кривой от начала координат O до точки A не выходит за рамки прямоугольника с вершинами в этих A у точках. Тогда кривая делит прямоугольник на две части, одной из которых является криволинейная трапеция O х (рис. ). Находим, что площадь прямоугольника равна xy Рис., а площадь трапеции x y dx для положительных x и a y dx для x 7

18 отрицательных x, при этом площадь трапеции должна составлять /4 или 3/4 от площади прямоугольника. Возможны четыре случая. Если точка A лежит в первой x четверти, то 4 ydx = xy или 4 ydx = 3xy. Дифференцируя, получаем уравнения с разделяющимися переменными 4y = y+ xy или 4y = 3y+ 3xy, общие решения которых 3 3 имеют вид y = cx и y = c x. Аналогично если A лежит во второй четверти, то получаем уравнения третьей уравнения 4 ydx = xy или x x 4 4 ydx = xy или если в четвертой уравнения x 4 x x ydx = 3xy; если в x 4 4 ydx = 3xy ; и x ydx = xy или ydx = 3xy. Все эти случаи приводят к тем же решениям y = cx 3 и 3 y = c x. 3 Ответ: y = cx 3 и y = c x, где x и c, общее решение; правые ветви кубических парабол 3 y = x и 3 y = x частные решения. у Рис. Задача 9. Записать уравнения кривых, для любой точки которых абсцисса центра тяжести криволинейной трапеции, ограниченной осями координат, дугой этой кривой и отрезком, соединяющим данную точку с ее проекцией на ось абсцисс, составляет 9 % от абсциссы этой точки. х 8

19 для любой точки ( ) Решение. Будем считать, что кривая находится в верхней полуплоскости, так как из соображений симметрии очевидно, что при отображении кривой относительно оси абсцисс координата x с центра тяжести не меняется. Тогда A x ; y, где x >, должно выполняться условие S x x 9x xy dx =, или 9 xydx= x S. Подставив в это соотношение формулу площади трапеции и перейдя к произвольной точке ( x; y ), получим интегральное x x уравнение xydx= 9x ydx. Продифференцируем его по x переменной x: xy = 9 ydx+ 9xy снова интегральное уравнение. Приведем подобные и еще раз продифференцируем: y+ xy = 9 y дифференциальное уравнение с разделяющимися переменными. Общее решение имеет вид 8 y = cx. Легко проверить, что уравнение x x xydx= 9x ydx, верное для отрицательных x, приводит к этому же ответу. Итак, задача решена для положительных y, т.е. для c >, но, как было отмечено выше, ответ верен и для отрицательных y, т.е. для c 20 Глава. Физические задачи.. Задачи на движение При прямолинейном движении мгновенные скорость и ускорение определяются как первая и вторая производные соответственно от перемещения (пути), т.е. скорость vt () = s () t и ускорение at () = s () t = v () t, где s(t) перемещение точки за время t. Напомним, что если при прямолинейном движении тело не меняет направления движения, то понятия перемещения и пройденного пути совпадают. Пусть теперь данное движение вызвано силой F, направленной вдоль прямой движения. Тогда по второму закону Ньютона F = ma = ms. В обычно встречающихся задачах сила зависит от расстояния s или скорости v, что приводит к дифференциальному уравнению ms = F() s или mv = F() v. Далее мы рассмотрим три примера действующей силы: силу сопротивления, силу упругости и центробежную силу. Сила сопротивления. Как показывает опыт, если тело при движении испытывает сопротивление среды, то сила этого сопротивления возрастает при увеличении скорости тела. При этом если скорость движения невелика и тело имеет малые размеры, то силу сопротивления можно считать пропорциональной скорости (например, сопротивление воды при движении плавучего средства по ее поверхности или при погружении небольшого объекта в воду). Если же скорость и размеры предмета велики, то сопротивление становится пропорциональным квадрату скорости (например, свободное падение большого тела в воздухе). Итак, сила сопротивления Fr =μ v или Fr =μv, где μ коэффициент сопротивления. Часто для удобства коэф-

21 фициент μ уменьшают в m раз, где m масса движущегося тела, т.е. записывают Fr =μ mv или Fr =μmv, что по- зволяет сократить на ненулевой множитель второй закон Ньютона. Действительно, если, например, на тело действует только сила сопротивления, то получаем уравнения mv = μmv или mv = μmv, которые сокращаются до v = μv или v = μv. Знак минус в этих уравнениях показывает, что сила сопротивления (а значит, и вызываемое ею ускорение) имеет направление, противоположное скорости движения тела. Сила упругости. Если пружина находится в состоянии покоя, то по первому закону Ньютона, равнодействующая всех сил, действующих на нее, равна нулю. Однако закон Гука утверждает, при небольшой деформации пружины, т.е. при изменении ее длины, возникает сила упругости, пропорциональная величине этого изменения, которая стремится вернуть пружину в исходное положение. Следовательно, при рассмотрении колебаний пружины достаточно рассматривать силу упругости Fe = ks, где k коэффициент жесткости пружины; s отклонение от положения равновесия, и, возможно, силу сопротивления движению пружины, остальные же силы (в том числе сила тяжести) уравновешивают друг друга. Таким образом, второй закон Ньютона приводит к дифференциальному уравнению второго порядка ms = ks, или ms = μs ks, или ms = μ( s ) ks. Здесь через m обычно обозначают массу груза, прикрепленного к пружине, массой же самой пружины, как правило, пренебрегают. Знак минус указывает на то, что сила упругости направлена в сторону, противоположную отклонению пружины, а сила сопротивления противоположна вектору скорости. Центробежная сила. На тело массой m, движущееся по окружности радиуса r с угловой скоростью ω, действует

22 центробежная сила Fc = mω r, направленная от центра окружности вращения. Также заметим, что если тело движется не по прямой, а в плоскости или в пространстве, то задача обычно сводится уже не к одному дифференциальному уравнению, а к системе двух или трех уравнений соответственно. Связано это с тем, что описанные выше соотношения приходится рассматривать для проекций векторов перемещения, скорости, ускорения и силы на оси координат. Например, векторное равенство v = s приводит к трем скалярным равен- ствам vx = x, vy = y и vz = z, где v x, v y и v z проекции скорости; x, y и z координаты движущейся точки. Задача. Под действием сопротивления воды лодка за мин замедлила свое движение с 6 до км/ч. Какой путь пройдет лодка до полной своей остановки? Решение. Пусть v(t) это скорость лодки в момент времени t. Лодка замедляет свое движение за счет силы сопротивления воды, пропорциональной скорости лодки: Fr =μ mv. Тогда второй закон Ньютона приводит к дифференциальному уравнению с разделяющимися переменными v = μ v, решение которого имеет вид v= ce μt. Воспользовавшись условиями v () = 6 и μ v =, получим, 6 6 что c = 6 и 6e =, откуда e μ = 6 6. Следовательно, 6t скорость движения лодки задается уравнением v = 6. Из данного равенства видно, что теоретически в любой конечный момент времени скорость лодки положительна и остановка может произойти только при t =. Итак, путь

23 + 6t + 6t 6 s = 6 dt = =,558 км, т.е. чуть 6ln 6 ln 6 менее 56 м. 6t Отметим, что функция v = 6 очень быстро приближается к нулю. Например, уже через мин скорость будет составлять меньше одной десятой миллиметра в час, т.е. практически равной нулю. Поэтому при расчете пути лодки до ее полной остановки несобственный интеграл можно заменить определенным s 6 6t = 6 dt, при этом погрешность будет крайне незначительной, меньшей, чем одна тысячная миллиметра. Ответ: 55 м 8 см. Задача. Мяч весом 4 г брошен вверх со скоростью м/с. Известно, что на мяч, летящий со скоростью м/с, воздух оказывает сопротивление 5 Н. Считая ускорение свободного падения равным м/c, найти наибольшую высоту подъема мяча. Решение. Пусть v(t) это скорость мяча в момент времени t. На движение мяча оказывают влияние направленные вниз сила тяжести F = mg и сила сопротивления воздуха, пропорциональная квадрату скорости, g r =μmv. Для нахождения коэффициента μ заметим, что если v = м/с и m = 4 г, то F = 5 Н. Следовательно, μ= F r 5,5 mv = 4 = м. Теперь запишем второй закон Ньютона: ma = Fg Fr или mv = m,5mv r. Сокращая на массу, получим уравнение v’ =,5v. Разделим переменные: 3 F

24 dv = dt, и проинтегрируем левую часть:,5v + dv = 8 dv = arctg v c,5v + +. Затем из v + 8 v найденного общего решения arctg = c t выразим скорость: v = tg. c t Наивысшей точки своего полета мяч достигает в тот момент, когда его скорость равна нулю, т.е. при t = c. Следовательно, наибольшую высоту можно найти как путь, пройденный в промежуток времени от t = до t = c, т.е. c c t c t c h= tg dt = 8ln cos = 8ln cos. t= Итак, для получения окончательного ответа осталось найти значение константы c. По условию задачи v () =. Подставив эти значения в общее решение, находим, что c = arctg, 3 8ln cos arctg 4ln 6, (мы использовали формулу cos arctg a = + a ). Ответ: 6 м см. Задача. Груз массой 3 г подвешен на легкой пружине и выведен из состояния покоя вытягиванием пружины на 8 см, при этом возникла сила упругости Н. Затем груз подбросили вертикально вверх, придав ему начальную скорость,5 м/с. Найти период и амплитуду свободных колебаний груза, если движение происходит без сопротивления. t= c 4

25 Решение. Обозначим через s(t) отклонение груза от положения равновесия. Колебания вызываются силой упругости Fe = ks, причем так как при удлинении пружины на 8 см сила упругости составила Н, то коэффициент жесткости k =,5,8 = кг/c. Запишем второй закон Ньютона ma = ks, откуда получим линейное однородное уравнение второго порядка,3s +,5s=. Характеристиче- ское уравнение,3λ +,5 = имеет корни λ, =± 6, 5i, значит, общее решение записывается в виде s = c cos 6, 5t+ c sin 6, 5t. Для нахождения констант заметим, что s() = с =,8 и v() = s () = 6,5с =,5. Следовательно, c =,8, c =,8 и уравнение колебательного движения имеет вид s =,8cos 6, 5t+,8sin 6, 5t, или, если ввести вспомогательный угол, s=,8 sin 6,5t+. Таким образом, π 4 амплитуда колебания равна, 8,3 м, а период π с. 6, 5 Ответ: период с; амплитуда см 3 мм. Задача 3. Найти уравнение движения груза массой г, закрепленного на легкой вертикальной пружине с коэффициентом жесткости 5 кг/с, если первоначально груз был отклонен от положения равновесия на см и затем отпущен без начальной скорости. Известно, что при движении данного груза со скоростью м/с сопротивление воздуха составляет Н. Решение. Пусть s(t) это отклонение груза от положения равновесия в момент времени t. На груз действуют си- 5

26 ла упругости пружины Fe = 5s и сила сопротивления воздуха, которую будем считать пропорциональной скорости груза, т.е. Fr =μ v =μ s, где μ=, кг/с. Получим дифференциальное уравнение, s =,s 5s, или, s +,s + 5s=. Характеристическое уравнение имеет, корни λ, = ±, 4, 5 ± 5i, поэтому общее, 4 решение выглядит следующим образом:, 5 s= e t ( ccos5t+ csin5 t). Дифференцируя, найдем скорость груза:,5 v= e t (,5ccos5t,5csin5t 5csin5t+ 5ccos5 t), и из начальных усл овий s () =, и v () = вычислим константы: c =, и c =,. Следовательно, оконча- тельно уравнение движения груза приобретает вид,5 t s = e (,cos5t+,sin 5 t ). Ответ:,5 t s = e (,cos5 t+,sin 5 t). Задача 4. Трубка с находящимся в ней шариком равномерно вращается вокруг перпендикулярной к ней верти- в момент времени t. Угловая скорость вращения кальной оси, причем за десять минут трубка делает три полных оборота. Чему станет равным расстояние от шарика до оси через минуту после начала вращения, если изначально оно равнялось 4 см и шарик имел нулевую скорость? Решение. Пусть r(t) это расстояние от шарика до оси вращения 6π трубки равна =, π рад/c. Учитывая действующую 6 на шарик центробежную силу = (, π ) mr, где m Fc масса шарика, составим уравнение 6 mr = (, π) mr, или

27 r (, π ) r =. Характеристическое уравнение λ (, π ) = имеет корни λ, =±, π, значит,, t, π t r ce π = + ce. Из начальных условий r () =, 4 и r () = видно, что c = c =, и r =,4ch,πt. Подставляя в качестве времени 6 с, получим r =,4ch,6π,35 м. Ответ: 3 см 5 мм. Задача 5. Горизонтальная трубка вращае тся с угловой скоростью, рад/c вокруг вертикальной оси. В трубке на- пружина длиной см и коэффициентом жестко- ходится сти,48 кг/c, к концам которой прикреплены грузики массой 6 г и 4 г, причем в момент начала вращения пружина не растянута и грузики одинаково удалены от оси вращения. Найти зависимость изменения длины пружины от времени. Решение. Пусть r (t) и r (t) это расстояния в метрах от оси вращения до первого и второго грузиков соответственно (первым будем считать грузик в 6 г, а вторым грузик в 4 г) в момент времени t. В процессе вращения под действием центробежных сил Fc =,6, r =,4r и Fc =, 4, r =,6r грузики начинают удаляться от оси вращения, что приводит к растягиванию пружины. Возникает сила упругости. Заметим, что удлинение пружины равно разности между длиной пружины в текущий момент времени и первоначальной длиной, т.е. ( r+ r,) м. Следовательно, сила упругости составляет Fe =, 48( r+ r,) Н, причем она направлена в сторону оси вращения, т.е. противоположна направлению центробежных сил. 7

28 Получаем систему дифференциальных уравнений,6r =,4r,48( r+ r,). Вычтя из первого, 4r =, 6r, 48( r+ r,) уравнения второе,6r, 4r =,4r,6r и введя новую переменную zt () =,6r,4r, получим линейное однородное уравнен ие второго порядка z, 4z =, об-,t,t щее решение которого имеет вид z = ce + c e. Возвращаемся к исходным переменным:,t,t,6r, 4r = ce + ce. В нач альный момент времени грузики находилис ь на расстоянии 5 см от оси вращения и имели нулевую скорость, т.е. r() = r() =,5 и r () = r () =. Эти условия приводят к системе уравне- ний c+ c =,, из которой c = c =,5 и c c = ( ),,6r e e,c. 4r,5 t = + t = h t. Из данного равенства выразим одну из переменных, например r =,5r,5ch,t, и подставим ее в любое уравнение искомой системы, например в первое:,6r =,4r,48(,5r, 5ch,t,). После раскрытия скобок и приведения подобных уравнени е примет вид,6r +,76r =,ch, t +,48. Характеристическое уравнение,6λ +,76 = имеет корни λ, =±, 4i, поэтому r = c si n,4t+ c cos,4t решение однородного уравнения,6r +,76r =. Частное решение неоднородного уравнения будем исвиде r = Ach, t+ Bsh, t+ C. кать в Тогда 8

29 r =,4Ach, t+,4bsh, t. После подстановки этих выражен ий искомое уравнение приобретает вид, Ach,t+, Bsh,t+,76C =,ch t+,48, откуда A = =,, B = и C = =. Значит. 76 49,,48 общее решение неоднородного уравнения записывается в ch, t виде r = csin, 4t+ ccos,4t Еще раз воспользовавшись начальными условиями r () =,5 и r (), получим = c +, + =, 5 и 49, 4c =, откуда c = и c =. Следовательно, закон 5 движения первого грузика окон чательно описывается соотношением r ch, t cos, 4t = +. А закон движения 5 49 второго грузика имеет следующий вид: 3 ch,t 3cos,4t r =,5r,5ch, t =. Длина пружины равна сумме найденных расстояний: r+ r = 5 cos,4t Ответ: 5 cos,4 t Задача 6. Однородная цепь длиной,5 м соскальзывает с горизонтального стола, причем в начальный момент времени со стола свисает конец длиной см. Пренебрегая трением и считая ускорение свободного падения равным м/c, найти время соскальзывания всей цепи. Решение. Пусть l(t) это длина в метрах свисающей со стола части цепи в момент времени t. Силой, под действи- 9

30 g ная плотность цепи. Из второго закона Ньютона следует, что F = Ma=,5ρ l (здесь m=ρ l масса свисающей g ем которой движется цепь, является сила тяжести свисающей части F = mg = ρ l, где через ρ обозначена линей- части цепи, а M =,5ρ масса всей цепи). Получаем дифференциальное уравнение ρ l =,5ρ l, или,5l l = это линейное однородное уравнение с постоянными коэффициентами второго порядка. Характеристическое уравнение,5λ = имеет t t корни λ, =±, значит, l = ce + ce. Неизвестные константы можно найти, исходя из начальных условий l() =, и l () =, которые приво дят к системе уравне- c+ c =, ний, откуда c = c =,5, и решение прини- c c = t t мает вид l =,5( e + e ) =,ch t. Для нахождения времени соскальзывания всей цепи надо принять длину l равной,5, =, 4 м. Получим arcch 4 ln ( ) = и, 4,ch t t = =, 94 с, т.е. чуть меньше двух секунд (мы воспользовались формулой arcch a ln( a a ) = + ). Ответ:, 94 с. Задача 7. На противоположных берегах реки шириной 5 м расположены два пункта A и B, причем отрезок AB перпендикулярен берегам. Катер с собственной скоростью 8 км/ч переправляется из A в B так, что в любой момент времени его нос направлен в точку B. Найти время переправы, если скорость течения реки равна км/ч. 3

31 Решение. Введем систему координат, причем точку B поместим в начало координат, ось ординат расположим вдоль отрезка AB, а направление оси абсцисс выберем совпадающим с направлением течения реки (рис. ). По условию задачи если в момент времени t катер на- Ct () = xt (); yt (), то ходится в точке ( ) у A 8 C вектор его скорости направлен вдоль отрезка CB. Обозна- ϕ( t ) угол ме- чим через ρ () t длину отрезка CB, а через жду отрезком CB и осью абсцисс, т.е. фактически введем полярные коорди наты. Тогда из чертежа видно, что x = 8cosϕ и y = 8sinϕ. Подставив в эти равенства формулы перехода к полярным координатам x =ρcos ϕ и y =ρsin ϕ, получим систему дифференциальных уравнений с двумя неизвестными ρ cos ϕ ρϕ sin ϕ= 8cos ϕ. Разрешим данную систему ρ sin ϕ+ρϕ cosϕ= 8sin ϕ относительно выражений ρ и ρϕ. По формулам Крамера cosϕ sinϕ найдем определители: Δ= = cos ϕ+ sin ϕ= ; sin ϕ cos ϕ B ϕ Рис. Δ = 8cosϕ sinϕ c os 8sin ρ 8sin cos = os ϕ ϕ ϕ 8c ϕ ϕ= = cosϕ 8; cos ϕ 8cos ϕ Δ ρϕ = = 8 cos ϕsin ϕ sin ϕ+ 8 cos ϕsin ϕ= sin ϕ 8sin ϕ = sin ϕ. Тогда ρ= cosϕ 8 и ρϕ = sinϕ. Итак, нам удалось существенно упростить нашу систему уравнений:. Теперь из второго уравне- ρ = cosϕ 8 ρϕ = sinϕ 3 х

32 ния выразим sinϕ ρ=, продифференцируем: ϕ ( ϕ ) cosϕ ϕ sin ϕ ϕ sin ϕ ρ= = cosϕ, и подставим в первое уравнение: cos cos 8 ( ϕ ) ( ϕ ) ϕ sinϕ ϕ= ϕ, или ( ϕ ) ϕ sin ϕ cos 4 = ϕ это уравнение второго порядка, не ( ϕ ) содержащее независимую переменную t. Для решения этого уравнения сделаем замену ϕ= p( ϕ ) ppsin ϕ и ϕ = p p. Имеем = cosϕ 4 уравнение с p разделяющимися переменными. Разделим пер еменные: dp cosϕ 4 = dϕ. Проинтегрируем отдельно правую p sin ϕ cos ϕ dϕ d(sin ϕ) d(tg ϕ ) часть: dϕ 4 = 4 = sin ϕ sin ϕ sin ϕ tg ( ϕ ) = ln sinϕ 4ln tg( ϕ ) + lnc. Тогда общее решение для функци и p( ϕ ) имеет вид p = csin ϕ 4 tg ( ϕ ). Чтобы найти константу c, заметим, что в начальный момент времени точки π A и C совпадали, а значит, ϕ () = и ρ () =,5. Тогда из второго уравнения системы ρϕ = sinϕ видно, что ϕ () = 4, а значит, p π = 4. Подставив эти значения в 4sin ϕ общее решение, найдем c = 4 и p = 4. tg ( ϕ ) 3

33 Вернувшись от переменной p к переменной ϕ, получим 4sin ϕ уже уравнение первого порядка ϕ=, откуда 4 tg ( ϕ ) 4 tg ( ϕ ) dϕ= 4 dt. Для интегрирования левой части еще sin ϕ раз применим основную тригонометрическую подстанов- 4 tg ( ϕ ) ку: dϕ= tg ( ϕ ) ( + tg ( ϕ ) ) d( tg( ϕ ) ) = sin ϕ 3 tg ( ϕ ) = ( ) ( ) tg ( ϕ ) d tg( ϕ ) + tg 4 ( ϕ ) d tg( ϕ ) = tg ( ϕ ) + + c, а затем для ϕ () t запишем общее решение 3 5 tg ( ϕ ) tg ( ϕ ) = c 4t, или 5 tg ( ϕ ) + 3tg ( ϕ ) = 6 π = c t. Так как ϕ () =, то c = 8. Далее выразим ρ через ϕ. Для этого в выражение sinϕ 4sin ϕ ρ= подставим ϕ= и получим, что 4 ϕ tg ( ϕ ) 4 tg ( ϕ ) ρ =. Осталось заметить, что в момент окончания sinϕ 4 tg ( ϕ ) переправы р адиус-вектор ρ=, а значит, =, отчто и угол ϕ=. Это условие позволяет sinϕ куда видно, из 3 5 общего решения 5 tg ( ϕ ) + 3tg ( ϕ ) = c t выразить c 8 время переправы: t = = = ч, т.е. 4 мин. 5 Ответ: 4 мин. 33

34 .. Задачи на реактивное движение При движении тела с переменной массой (например, космически й корабль) второй закон Ньютона не применим, так как он справедлив только для тел с постоянной массой. В этом случае используют так называемое уравнение Мещерского mv = F + um, где m(t) масса тела; v(t) его скорост ь; F(t) действующая на него сила в момент времени t. Через u(t) обозначена относительная (относительно самого движущегося тела) скорость частиц, присоединяющихся к телу, или, наоборот, отсоединяющихся от него. При движении космической ракеты u это скорость истечения продуктов горения из сопла ракеты, причем в этом случае ускорение v и скорость истечения газов u имеют противоположные направления. Величину m, характеризующую скорость изменения массы тела, называют секундным расходом массы. Заметим, что если масса тела постоянна, то секундный расход равен нулю и уравнение Мещерского превращается во второй закон Ньютона. В случае же летательного аппарата с реактивным двигателем секундный расход отрицателен, так как масса аппарата уменьшается в ходе движения. В простейших моделях секундный расход топлива считают постоянным. Задача 8. Ракета с нулевой начальной скоростью движется прямолинейно под действием отдачи от струи газа, исходящей со скоростью км/с. Масса ракеты с полным запасом топлива равна 4 т, без топлива 5 т. Найти скорость движения ракеты после сгорания всего топлива, пренебрегая силой тяжести и сопротивлением воздуха. Решение. Пусть m(t) и v(t) это масса и скорость ракеты соответственно в момент времени t. Тогда уравнение 34

35 Мещерского запишется в виде mv = m или dv dm m =. Домножив обе части равенства на dt и введя в рассмотрение функцию v(m), получим дифференци- dt dt альное уравнение с разделяющимися переменными mdv = dm. Имеем dv = dm и v= lnm+ c общее m решение. Из условия v (4) = находим, что c = ln 4 и 4 v = ln частное решение. Подставив m = 5, полу- сгорания топлива скорость корабля достиг- m чим, что после 4 нет значения v = ln = ln8 4,6 км/с. 5 Ответ: 4,6 км/с. Комментарий. Отметим, что в ходе решения данной задачи мы фактически вывели формулу скорости космического аппарата v= uln M, которая впервые была получена Циолковским в m 897 году и сейчас носит его имя. В этой формуле через M и m обозначены начальная и конечная (после выработки топлива) массы космического аппарата, через u скорость газовой струи. Скорость ракеты v, вычисляемую по формуле Циолков- называют характеристической. Реальная же скорость, как ского, правило, ниже характеристической из-за влияния сил гравитации и сопротивления среды, а также из-за потерь, вызванных затратами на управление движением космического корабля. Задача 9. Ракета с начальной массой 5 т движется вертикально вверх под действием силы тяги реактивного двигателя. Скорость истечения газов и секундный расход топлива постоянны и равны 3 км/c и т/с соответственно. На какую высоту поднимется ракета через минуту после 35

36 старта, если на поверхности Земли скорость ракеты равна нулю? Сопротивлением воздуха пренебречь. Решение. Пусть m(t) и v(t) это масса и скорость ракеты соответственно в момент времени t. На движение ракеты оказывают влияние сила тяги двигателя ракеты и сила тяжести Земли F = mg. Значит, уравнение Мещерского g запишется в виде mv =, m 3m (ускорение свободного падения считаем равным, км/с, численное значение расхода топлива пока не подставляем). Выразим ускорение: v =, 3 m, и проинтегрируем обе части по времени: v=,t 3ln m+ c. Так как в момент старта ско- m рость ракеты нулевая, а масса составляет 5 т, то 5 c = 3ln 5 и v= 3ln,t. m Ита к, для нахождения скорости ракеты в произвольный момент времени осталось выразить массу ракеты через время. Так как секундный расход топлива m = т/с, то, интегрируя, н аходим, что m= c t, где при t = видно, что c = 5 и m= 5 t. Подставив выражение для массы ракеты в выведенную нами формулу скорости, получим 5 v= 3ln,t = 3ln(,4 t),t. 5 t Высоту подъема ракеты за одну минуту найдем как интеграл от скорости: ,57 км. Ответ: 5 км 57 м h= ln(,4 t) dt, tdt = = (75 3 t)ln(,4 t) + 3t,5t = 57ln,

37 Комментарий. Достаточно небольшая высота подъема ракеты показывает, что напрямую использование аппаратов с реактивным двигателе м для преодоления силы тяжести Земли нерационально. На практике в современной космонавтике используются более сложные многоступенчатые ракеты-носители. При этом расчеты скорости и высоты подъема каждой отдельной ступени осуществляются по тем же принципам, что и в приведенных в данном параграфе задачах..3. Задачи на радиоактивный распад Радиоактивным распадом называют самопроизвольное превращение ядер атомов некоторых элементов в ядра других элементов. Радиоактивный распад носит статистиче- изо- ский характер: ядра атомов распадаются не одновременно все сразу, а в течение времени существования данного топа. Экспериментальным путем установлено, что мгновенная скорость радиоактивного распада пропорциональна количеству вещества, имеющемуся в данный момент, т.е. m = λ m, где m масса нераспавшегося вещества; λ постоянная распада. Знак минус берется потому, что масса вещества уменьшается, а значит, скорость его изменения отрицательна. Время, в течение которого распадается половина имеющегося вещества, называется периодом полураспада. Периоды полураспада основных радиоактивных изотопов приводятся в физических справочниках, например для радона он составляет около четырех суток, для радия 6 веков, для плутония более 4 тысячелетий, а для урана-38 4,5 миллиарда лет. Задача. Согласно опытам в течение года из каждого грамма радия распадается,44 мг. Через сколько лет распадется четверть имеющегося радия? 37

38 Решение. Пусть m(t) это масса оставшегося радия к моменту времени t, где время измеряется в годах. Закон радиоактивного распада приводит к уравнению с разделяющимися переменными m = λ m, общее решение кото- рого имеет вид m= ce λt. Подставив t =, увидим, что константа c совпадает с величиной массы радия в начальный момент времени, т.е. c= m(), и m= m() e λt частное решение. Из условия задачи следует, что за год распадается,44 % имеющегося радия, следовательно, к концу первого года останется 99,956 % радия, т.е. m() =,99956 m(). Подставляя в частное решение, находим, что e λ =,99956 и m= m(),99956 t. Если ко времени t распалась четверть радия, то mt () =,75 m(). Получим,75 m() = m(),99956 t, откуда, t = log,99956, , 679 года, т.е. примерно 653 года 8 месяцев и 4 дня. Ответ: 653 года 8 месяцев и 4 дня. Задача. В куске горной породы содержится мг урана и 3 мг уранового свинца. Известно, что при полном ра спаде 4 г урана образуется 8 г уранового свинца. Считая, что в момент образования горная порода не содержала свинца, определить возраст этой горной породы. Решение. Пусть m(t) это масса в миллиграммах нераспавшегося изотопа урана через t лет после формирования породы. Тогда m = λ m и m= m() e λt. В момент образования породы, кроме мг урана, в ней также содер- жалось некоторое количество урана, превратившегося затем в свинец. Следо вательно, m () = + 3 = 5 мг 4 8 и m= 5e λt. 38

39 9 4,5 Зная, что период полураспада урана составляет около 4,5 миллиардов лет, вычислим, что через этот срок остане тся,5 5 = 57,5 мг урана, а значит, 57,5 = 5e λ. 9 9 λ 4,5 4,5 t Отсюда e = и m = 5. Осталось в эту формулу массы урана подставить m = и выразить время: t = 4,5 ( log log5) 97 лет. 9 6 Ответ: 97 миллио нов лет.. 4. Задачи на смеси В сводящихся к дифференциальным уравнениям задачах на смеси обычно делается следующее допущение: песмеси происходит настолько ремешивание компонентов интенсивно, что в любой момент времени смесь можно считать однородной, т.е концентрация ее компонентов одинакова во всей смеси. Если бы при этом концентрация p некоторого компонента была постоянной во времени, то, зная скорость изменения объема смеси v (л/с), можно было бы найти, что за время Δt объем компонента изменится на Δ V = pvδ t литров. Однако, как правило, концентрация зависит от времени, и поэтому можно лишь записать, что изменение объема компонента лежит в промежутке между числа ми p() t vδ t и p( t+δt) vδ t. Если теперь эти неравенства разделить на Δt и перейти к пределу при Δt, то получим дифференциальное уравнение V = pv. Задача. В баке находится 5 л морской воды, со- держащей 4 % соли. В бак непрерывно подается пресная вода со скоростью 4 л/мин. Полученная смесь перемешивается и вытекает со скоростью 6 л/мин. Какой станет концентрация соли через час? 39

40 Решение. Пусть V(t) это объем соли в литрах, находящейся в баке в момент времени t, где время измеряется в минутах. Так как каждую минуту из бака вытекает на два литра жидкости больше, чем втекает, то ко времени t в баке будет (5 t) литров жидкости, а значит, концентрация соли составит. Vt () 5 t За небольшой промежуток времени Δt из бака выльется 6Δ t литров смеси. Если в течение этого промежутка конь неизменной, то данные 6Δ t литров центрацию считат Vt () 6Δt смеси содержат литров соли. На самом же деле 5 t концентрация уменьшается, поэтому верно неравенство V() t 6Δt Δ V = V() t V( t+ Δ t) +Δ Δ. Деля эти неравенства на 5 t Δt и устремляя его к нулю, получим выражение для скоро- объема соли V =. Это уравнение 6V сти уменьшения 5 t dv 3dt с разделяющимися переменными. Имеем =, от- V t 75 куда lnv = 3ln t 75 + ln c, или V = c t 75. Так как в на- чальный момент времени концентрация соли составляла 6 4 % от 5 литров, то V () = 6, поэтому c = и t V = 6. Через 6 мин объем и концентрация соли бу

41 6 дут соответственно равны V (6) = и = 5 =,6 =,6 %. 3 5 (5 ) Ответ:,6 %. Задача 3. Сосуд объемом 5 л содержит воздух (8 % азота и % кислорода). В сосуд втекает, л азота в секунду, который непрерывно перемешивается, и вытекает такое же количество смеси. Через сколько времени в сосуде будет 9 % азота? Решение. Пусть V(t) это объем азота в момент времени t. Тогда за время Δt в сосуд втечет, Δ t, а вытечет не Vt (),Δt Vt ( +Δt),Δt менее и не более литров азота 5 V (здесь концентрация азота). Следовательно, изменение объема азота Δ V в сосуде удовлетворяет неравенству 5, Δ+ t,4 V( t) Δ t 42 8 Из начального условия V () = 5 = 4 л находим,4t частное решение V = 5 e. Осталось в данную формулу подставить V = 5 = 45 л и найти время 9 t = 5 ln 73,3 с, т.е. немного меньше трех минут. Ответ: мин 53 с..5. Задачи на охлаждение и нагревание В задачах на охлаждение или нагревание тела при взаимодействии с окружающей средой температуру окружающего пространства T c принято считать постоянной. Согласно закону, установленному Ньютоном, скорость охлаждения или нагревания тела пропорциональна разности температур тела и окружающей среды, т.е. T = k( T T c ), при этом если в начальный момент времени температура тела T больше температуры окружающего пространства T c, то происходит охлаждение и скорость T отрицательна, а если T . Сделанное замечание объясняет, почему коэффициент пропорциональности k обычно записывают со знаком минус. Само значение величины k зависит как от физических свойств тела, так и от его геометрической формы. Для нахождения коэффициента, как правило, измеряют температуру тела в некоторый промежуточный момент времени. Часто встречаются задачи о нагревании жидкости погруженным в нее электрическим прибором (металлический стержень, спираль, кипятильник и т.д.) с силой тока, мало меняющейся во времени. В этом случае опираются на явление, называемое Джоулевым теплом: если сила тока по- 4

43 стоянна, то вся электрическая энергия превращается в тепловую. Для нахождения тепловой энергии пользуются формулой E = cmδ T, где c удельная теплоемкость жидкости (в частности, для воды c 4 Дж/(кг C)); m масса жидкости; ΔT изменение температуры, а для нахождения электрической энергии формулой E =, где U Δt R U напряжение, подаваемое на прибор; R сопротивление прибора; Δt продолжительность протекания тока. Как правило, считают, что температура не оказывает заметного влияния на теплоемкость жидкости, изменение же сопротивления прибора иногда учитывают, а иногда нет. В действительности сопротивление проводников немного увеличивается с повышением температуры, а именно верна формула R = R( +α ( T T )), где R сопротивление при начальной температуре T ; α температурный коэффициент сопротивления. В большинстве справочников приводятся значения сопротивления R при температуре T = C. Задача 4. Тело охладилось за мин от 7 до 4 C. Температура окружающей среды поддерживается равной 5 C. Сколько еще минут понадобится, чтобы тело остыло до 3 C? Решение. Пусть T(t) это температура тела в момент времени t, где температура измеряется в градусах Цельсия, а время в минутах. Тогда по закону Ньютона T = k( T 5) это уравнение с разделяющимися переменными. Решаем его: = kt, ln( T 5) = ln c kt и dt T 5 kt T = ce + 5. Из условий T () = 7 и T () = 4 находим, 43