Экономические задачи с решение дифференциального уравнения

Задачи экономического содержания и дифференциальные уравнения, Монако Т.П., 2016

Задачи экономического содержания и дифференциальные уравнения, Монако Т.П., 2016.

Сборник задач предназначен для студентов высших учебных заведений. обучающихся по экономическим специальностям и изучающим математические дисциплины в соответствии с образовательными стандартами. Приведены разноуровневые экономические задачи, решение которых требует широкомасштабного использования аппарата дифференциальных уравнений. Представлен необходимый теоретический материал, позволяющий решать различные экономические проблемы методами дифференциальных уравнений. Некоторые параграфы содержат необходимый теоретический материал.
Данный задачник будет полезен студентам, аспирантам, преподавателям, а также все и всем желающим научиться применять математический инструментарий в экономических исследованиях и для успешного ведения бизнеса.

Уравнение инфляционного ожидания.
Согласно научным исследованиям на экономические процессы в условиях инфляции заметное влияние может оказывать настроение основной части населения относительно ожидаемого в будущем темпа роста цен. Так, если большая часть населения страны ожидает дальнейшего усиления роста цен, то она не станет вкладывать сбережения в банки, а будет покупать впрок товары повседневного спроса, менять деньги на твердую валюту. т.е. будет себя вести экономически разумно, и в результате темпы роста цен действительно будут увеличиваться.

Если же основная доля населения полагает, что в ближайшем будущем будет оживление в экономике и темпы инфляции снизятся, то люди будут больше покупать товаров длительного пользования и вкладывать деньги в банки (и, тем самым, инвестировать экономику страны), в результате. как правило, такое оживление в экономике действительно наступает.

Оглавление.
Предисловие.
§1. Задачи, приводящие к дифференциальным уравнениям.
1.1. Взаимосвязь функции спроса и эластичности.
1.2. Модель формирования равновесной цены на товар.
1.3. Модель естественного роста.
1.4. Задача об эффективности рекламы.
1.5. Уравнение инфляционного ожидания.
1.6. Задача о доходе и потреблении.
1.7. Закон логистического развития в инновационном менеджменте.
§2. Задачи экономического содержания, решаемые средствами дифференциальных уравнении.
ГЛОССАРИЙ.
Литература.

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Задачи экономического содержания и дифференциальные уравнения, Монако Т.П., 2016 — fileskachat.com, быстрое и бесплатное скачивание.

Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России. Купить эту книгу

Экономическая задача, приводящая к дифференциальному уравнению

Лекция 3-4

Обыкновенные дифференциальные уравнения

Общее и частные решения. Уравнения первого порядка. Уравнения с разделяющимися переменными. Однородные уравнения.

Линейные дифференциальные уравнения. Уравнение Бернулли.

Уравнений в полных дифференциалах.

Вопросы

1. Определение обыкновенных дифференциальных уравнений.

2. Дифференциальные уравнения первого порядка.

3. Общее решение дифференциального уравнения.

4. Задачи Коши. Частное решение.

5.Определение дифференциального уравнения 1-ого порядка.

6. Дифференциальные уравнения с разделяющимися переменными.

7. Однородные дифференциальные уравнения.

8. Линейные дифференциальные уравнения первого порядка.

10.Уравнение в полных дифференциалах

Различные вопросы экономики приводят к необходимости решения уравнений, содержащей в качестве неизвестной некоторую функцию и ее производные до определенного порядка n.

Экономическая задача, приводящая к дифференциальному уравнению

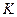
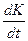
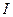
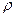
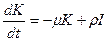
Обозначим — величина фондов в натуральном или стоимостном выражении. Фонды – это станки, помещения и т.п. они изнашиваются, стареют, как говорят, выбывают. Скорость выбытия фондов – это производная , она выражается через коэффициент выбытия . Например, если за 10 лет фонды полностью обновляются, то коэффициент выбытия равен =1/10. С другой стороны, инвестиции – вложение денег – ведут к увеличению фондов с коэффициентом пропорциональности . Учитывая все это, получим дифференциальное уравнение, вида:

.

Дата добавления: 2015-08-21 ; просмотров: 1126 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Решение экономических задач с использованием дифференциального уравнения второго порядка 1 page

Пример. Изменение стоимости продукции x(t) в тыс.руб. описывается дифференциальным уравнением:

.

— Записать x(0) и рассчитать и x_уст. По этим значениям построить качественно график функции.

— Найти экстремум функции (если он имеется).

— Выбрать правильно временной шаг – неделя, две недели, месяц.

— Составить таблицу и построить график изменения стоимости продукции x(t) за один год.

Заданное уравнение содержит всю необходимую информацию для его решения, т.к. начальные условия x(0) и могут быть рассчитаны по коэффициентам a и b.

Для начальных значений уравнение в матричной форме имеет вид:

.

Раскрывая это уравнение получим:

Из второго уравнения .

Третье уравнение перепишем с убыванием порядка производной

Сравнив третье уравнение с заданным, видно, что оно есть ни что иное, как заданное уравнение при t = 0

Для того чтобы записать вид решения, найдем корни характеристического уравнения. Необходимое для этого характеристическое уравнение получаем путем подстановки общего решения однородного дифференциального уравнения (см. предыдущий пример) в однородное дифференциальное уравнение

Получаем: .

Отсюда и учитывая, что получаем характеристическое уравнение:

.

Подставляя числовые значения коэффициентов, получаем:

,

Решая полученное уравнение, находим его корни:

Корни действительные. Поэтому вид решения дифференциального уравнения будет

,

что соответствует апериодическому процессу.

Найдя х_уст и коэффициенты интегрирования k₁ и k₂ , будем знать решение.

Теперь можно построить качественно график x(t). Для качественного построения графика необходимо знать x(0) , x’(0), х_уст и закон изменения x(t) (апериодический). Найдем:

x(0) = b₂ = 10 тыс.руб. (см. заданную размерность).

Все слагаемые в дифференциальном уравнении должны иметь одну и ту же размерность, поэтому с учетом размерности коэффициентов:

– имеет размерность ,

– также имеет размерность ,

а так как имеет размерность , то коэффициент а₁ должен иметь

размерность , таким образом .

Аналогично рассуждая запишем размерности остальных коэффициентов.

; b₂ = 10 тыс.руб., , .

Тогда из второго уравнения

Строим график качественно.

Кривая начинается при x(0) = 10, с положительной производной x’(0) > 0 (следовательно, функция должна иметь максимум) и стремится к х_уст= 3 по апериодическому закону (рис.8).

Для нахождения коэффициентов k₁ и k₂ необходимо иметь два уравнения. Одно нам уже известно: . Второе – получаем дифференцируя x(t):

Запишем два уравнения при t = 0 (начальные условия):

Перепишем их, подставив соответствующие значения:

Решение запишем:

Найдем значение t(0), при котором имеем x_max

, ;

Один месяц составляет от года [года], т.е. больше, чем найденное . Временной шаг при построении графика должен быть меньше t₀, поэтому следует строить график по одной неделе, принимая, что в месяце 4 недели.

Исходя из этого будем присваивать t следующие значения:

– за одну неделю,

– за две недели,

– за месяц.

Затем находим точки через каждый месяц и т.д.

Максимум существует при t = t₀ = 0,07.

= 3 + 24×0,705 – 17×0,497 = 3 + 16,91 + 8,44 = 11,47.

Данные расчетов сводим в таблицу

t			t0
x(t)	10,822	11,278	11,471	11,434	10,225

По данным таблицы строим количественно график изменения стоимости продукции (рис. 9).

Рис. 9.

ВОПРОСЫ ДЛЯ САМОПОДГОТОВКИ К ЗАЧЕТУ

1. Теорема Ферма и ее геометрический смысл.

2. Теорема Ролля и ее геометрический смысл.

3. Теорема Лагранжа, ее механический и геометрический смысл.

4. Порядок исследования функций.

5. Теоремы о возрастания и убывания функций.

6. Необходимые и достаточные условия существования экстремума функции.

7. Определение наибольшего и наименьшего значения функции на отрезке.

8. Определение выпуклости функции и точек перегиба. Асимптота графика функции.

9. Дифференциал функции и его геометрический смысл.

10. Неопределенный интеграл и его геометрический смысл.

11. Метод замены переменной при решении неопределенного интеграла.

12. Метод интегрирования по частям при решении неопределенного интеграла.

13. Интегрирование рациональных дробей .

14. Интегрирование тригонометрических функций.

15. Интегральная сумма и ее геометрический смысл.

16. Определенный интеграл, его геометрический и экономический смысл.

17. Свойства определенного интеграла.

18. Особенность применения метода замены переменной при решении определенного интеграла.

19. Особенность применения метода интегрирования по частям при решении определенного интеграла.

20. Геометрические приложения определенного интеграла.

21. Несобственные интегралы. Схождение несобственных интегралов.

22. Методика приближенного вычисления определенного интеграла.

23. Двойные и тройные интегралы, их геометрический смысл, основные свойства и правила вычисления.

24. Использование определенного интеграла в экономике.

25. Дифференциальные уравнения. Общее и частное решения дифференциального уравнения.

26. Теорема о существовании и единственности решения дифференциального уравнения и геометрический смысл.

27. Неполные дифференциальные уравнения первого порядка.

28. Виды дифференциальных уравнений первого порядка (уравнения с разделяющимися переменными, однородные уравнения, линейные уравнения).

29. Дифференциальные уравнения второго порядка. Методика понижения порядка дифференциального уравнения.

30. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами, особенности их решения.

31. Использование дифференциальных уравнений при решении экономических задач.

ПРИЛОЖЕНИЯ

Индивидуальные контрольные задания
по вариантам

Вариант №1.

1. Исследовать функции и построить графики

1.1. ;

1.2. ;

1.3. .

2. Найти наибольшие и наименьшие значения функции на отрезке:

2.1 на отр.[-1, 3];

2.2. на отр.[1, 4].

3. Доказать равенство:

3.1 ;

3.2. .

4. Найти интегралы:
4.1. ;
4.2. ;
4.3. ;
4.4. ;
4.5.
4.6. ;
4.7. ;
4.8. .

4. Вычислить определенные интегралы:
5.1. ;
5.2. ;
5.3. .

6. Проверить, является ли заданная функция y=f(x) решением данного дифференциального уравнения:

7. Решить задачу Коши: ,при .

8. Найти решение дифференциального уравнения и построить график. Внести начальное условие в правую часть дифференциального уравнения. Записать это уравнение.

, при .

9. Изменение стоимости продукции (в тыс. руб.) описывается заданным дифференциальным уравнением:

.

2) Записать y(0) и рассчитать и y_уст. По этим значениям построить качественно график функции.

3) Найти экстремум функции (если он имеется).

4) Выбрать правильно временной шаг – неделя, две недели, месяц. Составить таблицу и построить график изменения стоимости продукции y(t) за один год.

Вариант №2.

1. Исследовать функции и построить графики

1.1. ;

1.2. ;

1.3. .

2. Найти наибольшие и наименьшие значения функции на отрезке:

2.1. на отр. [0, 3];

2.2. на отр. [1, 4].

3. Доказать равенство:

3.1. ;

3.2. .

4. Найти интегралы:

4.1. ;

4.2. ;

4.3. ;

4.4. ;

4.5. ;

4.6. ;

4.7. ;

4.8. .

5. Вычислить определенные интегралы:

5.1. ;
5.2. ;
5.3. .

6. Проверить, является ли заданная функция y=f(x) решением данного дифференциального уравнения:

7. Решить задачу Коши: ,при .

8. Найти решение дифференциального уравнения и построить график. Внести начальное условие в правую часть дифференциального уравнения. Записать это уравнение.

, при .

9. Изменение стоимости продукции (в тыс. руб.) описывается заданным дифференциальным уравнением:

.

2) Записать y(0) и рассчитать и y_уст. По этим значениям построить качественно график функции.

3) Найти экстремум функции (если он имеется).

4) Выбрать правильно временной шаг – неделя, две недели, месяц. Составить таблицу и построить график изменения стоимости продукции y(t) за один год.

Вариант №3.

1. Исследовать функции и построить графики

1.1. ;

1.2. ;

1.3. .

2. Найти наибольшие и наименьшие значения функции на отрезке:

2.1. на отр.[0, 3];

2.2. на отр.[1, 4].

3. Доказать равенство:

3.1. ;

3.2. .

4. Найти интегралы:

4.1. ;

4.2. ;

4.3. ;

4.4. ;

4.5. ;

4.6. ;

4.7. ;

4.8. .

5. Вычислить определенные интегралы:

5.1. ;

5.2. ;

5.3. .

6. Проверить, является ли заданная функция y=f(x) решением данного дифференциального уравнения:

7. Решить задачу Коши: ,при .

8. Найти решение дифференциального уравнения и построить график. Внести начальное условие в правую часть дифференциального уравнения. Записать это уравнение.

, при .

9. Изменение стоимости продукции (в тыс. руб.) описывается заданным дифференциальным уравнением:

.

2) Записать y(0) и рассчитать и y_уст. По этим значениям построить качественно график функции.

3) Найти экстремум функции (если он имеется).

4) Выбрать правильно временной шаг – неделя, две недели, месяц. Составить таблицу и построить график изменения стоимости продукции y(t) за один год.

Вариант №4.

1. Исследовать функции и построить графики

1.1. ;

1.2. ;

1.3. .

2. Найти наибольшие и наименьшие значения функции на отрезке:

2.1. на отр.[0, 3];

2.2. на отр.[1, 4].

3. Доказать равенство:

3.1. ;

3.2. .

4. Найти интегралы:

4.1. ;

4.2. ;

4.3. ;

4.4. ;

4.5. ;

4.6. ;

4.7. ;

4.8. .

5. Вычислить определенные интегралы:

5.1. ;

5.2.

5.3. .

6. Проверить, является ли заданная функция y=f(x) решением данного дифференциального уравнения:

7. Решить задачу Коши: ,при .

8. Найти решение дифференциального уравнения и построить график. Внести начальное условие в правую часть дифференциального уравнения. Записать это уравнение.

, при .

9. Изменение стоимости продукции (в тыс.руб.) описывается заданным дифференциальным уравнением:

.

2) Записать y(0) и рассчитать и y_уст. По этим значениям построить качественно график функции.

3) Найти экстремум функции (если он имеется).

4) Выбрать правильно временной шаг – неделя, две недели, месяц. Составить таблицу и построить график изменения стоимости продукции y(t) за один год.

Вариант №5.

1. Исследовать функции и построить графики

1.1. ;

1.2. ;

1.3. .

2. Найти наибольшие и наименьшие значения функции на отрезке:

2.1. на отр.[0, 3];

2.2. на отр.[1, 4].

3. Доказать равенство:

3.1. ;

3.2. .

4. Найти интегралы:

4.1. ;

4.2. ;

4.3. ;

4.4. ;

4.5. ;

4.6. ;

4.7. ;

4.8. .