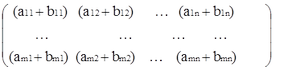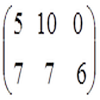Конспект урока «Решение экономических задач с использованием систем линейных уравнений» (10 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Тема урока: Решение экономических задач с использованием систем линейных уравнений.
Обобщение, систематизация и контроль знания учащимися основных понятий и законов по данной теме.
Развивать умения учащихся: самостоятельно применять знания в стандартных условиях, а также в изменённых нестандартных условиях; наблюдать; сравнивать; классифицировать. Развивать воображение.
Развивать умение видеть соотношения между явлениями реального мира и его математическими моделями, грамотно строить математические модели для встречающихся жизненных ситуаций.
Воспитывать такие качества личности, как познавательная активность, самостоятельность, упорство в достижении цели. Побуждать учеников к самоконтролю и взаимоконтролю своей деятельности.
Оборудование : мультимедийный проектор; на столах у учащихся рабочие листы с заданиями для самостоятельной и домашней работы.
Мотивационная беседа. Формулирование целей урока. Актуализация опорных знаний.
Людям, связанным по роду своей деятельности с экономическими процессами, как внутри одной страны, так и с мировой экономикой требуется твёрдое знание рыночных процессов и экономических законов. От этого будет зависеть как судьба малого частного предпринимательства, так и благосостояние целой страны. Такие знания надо постоянно совершенствовать, а начинать, конечно, надо с тех несложных задач, которые мы разбирали на предыдущих занятиях. Задачи такого рода типичны при прогнозах и оценках функционирования предприятий, экспертных оценках проектов освоения месторождений полезных ископаемых, а также в плани ровании микроэкономики предприятий.
Сегодня мы увидим, насколько вы готовы к выполнению таких работ, а также насколько слаженно вы сможете работать в команде. В связи с этим на первой половине урока каждой группе, а их будет пять, предстоит решить конкретную экономическую задачу, а так же ответить на вопросы, предлагающиеся к ним. На второй половине урока каждая группа демонстрирует нам решение своей задачи со всеми необходимыми пояснениями и комментариями, все остальные записывают себе это решение, задают возникающие вопросы.
На рабочих листах, предложенных вам, есть условия задач всех групп, а также 5 видов домашнего задания.
2 группа (Прогнозисты)
3 группа (контроль за рынком спроса и предложения )
4 группа (контроль за рынком спроса и предложения )
5 группа (Экспертная группа потребителей)
Сейчас предлагаю всем группам пересесть, чтобы совместно решать задачи.
Пятой группе предлагается поработать устно совместно со мной, так что вы располагайтесь за первыми партами.
Групповая самостоятельная работа в сочетании с индивидуальной работой.
(С использованием слайд-фильма).
4 группы учащихся работают по индивидуальным заданиям, после окончания работы (через 15 минут) каждая группа приводит решение своего задания.
Оставшаяся группа учащихся во время самостоятельной групповой работы работает устно вместе с учителем (отвечают на вопросы, предлагаемые в презентации).
Перед торговым предприятием возникла проблема – в каком соотношении закупить товары А и В: можно закупить 5 единиц товара А и 8 единиц товара В – всего за 92 тыс. р., а можно, наоборот, закупить 8 единиц товара А и 5 единиц товара В. Торговое предприятие остановилось на первом варианте, так как при этом экономится сумма, достаточная для закупки 2-х единиц товар А . Какова цена товара А и товара В?
Какие, по вашему мнению, товары могут иметь такую цену? Что лучше будет продаваться?
Обозначим через x и y соответственно стоимость единиц товаров А и В. тогда условие задачи можно записать так:
Решая эту систему, получаем:
Следовательно, стоимость одной единицы товара А – 12 тыс. р., а цена товара В – 4 тыс. р.
Предприятие выпускает три вида продукции, используя сырье трех типов. Необходимые характеристики производства указаны в таблице. Требуется определить объем выпуска продукции каждого вида при заданных запасах сырья.
Расход сырья по видам продукции, вес. ед./изд.
16.2. Использование систем линейных уравнений
Рассмотрим задачи, приводящие к составлению и решению систем линейных алгебраических уравнений.
6. Прогноз выпуска продукции по запасам сырья. Предприятие выпускает три вида продукции, используя сырье трех типов. Необходимые характеристики производства указаны в табл. 16.3. Требуется определить объем выпуска продукции каждого вида при заданных запасах сырья. Задачи такого рода типичны для прогнозов и оценок функционирования предприятий, экспертных оценок проектов освоения месторождений полезных ископаемых, а также для планирования микроэкономики предприятий.
Решение. Обозначим неизвестные объемы выпуска продукции через X1, X2 и X3. Тогда при условии полного расхода запасов для каждого вида сырья можно записать балансовые соотношения, которые образуют систему трех уравнений с тремя неизвестными:
Решая эту систему уравнений любым способом, находим, что при заданных запасах сырья объемы выпуска продукции составят по каждому виду соответственно (в условных единицах)
7. Общая постановка задачи прогноза выпуска продукции. Пусть
— матрица затрат сырья Т видов при выпуске продукции П Видов. Тогда при известных объемах запаса каждого вида сырья, которые образуют соответствующий вектор
Вектор-план 
Где индекс Т означает транспонирование вектора-строки в вектор-столбец.
Творческие проекты и работы учащихся
В процессе работы над индивидуальным проектом по математике «Матричная алгебра в экономике» учеником 11 класса гимназии были рассмотрены матричные методы в экономике на примерах решения задач экономического содержания. В работе доступно объясняется, что такое «математическая матрица» и как ее применять.
Подробнее о проекте:
Готовый творческий и исследовательский проект по математике «Матричная алгебра в экономике» наглядно демонстрирует взаимосвязь математики и экономики, определяет роль математических методов в анализе экономических процессов, объектов и явлений.
Оглавление
Введение
1. Немного истории.
2. Матрицы и операции над ними.
3. Решение с помощью матриц экономических задач.
Заключение
Используемая литература
Приложение
Введение
На современном этапе экономические взаимоотношения между субъектами образуют экономические системы со сложной структурой, большим количеством элементов и связей между ними, которые являются причиной почти всех особенностей экономических задач.
На внедрение и развитие математических методов в решении экономических задач, большое влияние оказало создание и развитие современной вычислительной техники. Вычислительная техника нового поколения позволила применять на практике множество новых методов, которые были описаны ранее только в теории или объяснялись на простых примерах.
Но никакая вычислительная техника не способна заменить человека и поэтому, люди должны уметь эффективно использовать теоретические знания в области математики в экономике, а именно, уметь правильно решать экономические задачи при помощи матричных методов.
Понятие матрицы и основанный на нем раздел математики — матричная алгебра — имеют чрезвычайно важное значение для экономистов. Объясняется это тем, что значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное — компактной матричной форме.
Также матрицы позволяют с минимальными затратами труда и времени обрабатывать огромный и весьма разнообразный статистический материал, различные исходные данные, характеризующие уровень, структуру, особенности социально-экономического комплекса.
В современных условиях особенно актуально использование матриц для формирования баз данных, ведь вся информация обрабатывается и хранится в форме матриц.
Матрицы можно эффективно использовать не только в науке, но и применять их на практике в крупных предприятиях для решения современных экономических задач. Матричный метод позволяет упростить работу человека, уменьшить количество критериев и альтернатив для выбора и получать выгодные варианты решения для выхода из различных экономических ситуаций.
В данной работе содержится информация о самих матрицах, операциях над ними и на примерах показано, как можно решать экономические задачи при помощи матриц.
Актуальность. Математика и экономика – две на первый взгляд далекие друг от друга науки. Однако, взаимосвязь между этими науками, роль математических методов в анализе экономических процессов, объектов и явлений были отмечены учеными ещё в XVII веке.
В XX веке происходило бурное проникновение математических методов в самые разные науки, в том числе и в экономику. В настоящее время этот процесс ещё более активизировался, благодаря развитию вычислительной техники. Поэтому современному экономисту необходима основательная математическая подготовка. И в число наиболее важных математических дисциплин для экономиста входит линейная алгебра, а именно матричная алгебра. В этом я вижу актуальность выбранной темы.
Цель. Рассмотреть матричные методы в экономике на примерах решения задач экономического содержания.
- На примере задач показать связь математики и экономики
- Научиться применять в экономике математический аппарат
- Показать роль математических методов в экономике (реальные задачи из разных сфер жизнедеятельности человека)
Гипотеза Используются ли в экономике те математические знания, которыми мы владеем
Предмет исследования: Матричные методы.
Объект исследования: Математические понятия и законы, экономические модели.
Методы исследования: Теоретическое изучение материала, образцы решения экономических задач.
Немного истории
В это же время был предложен другой метод решения систем линейных уравнений, который тоже носит имя своего изобретателя, это «метод Гаусса». Заметим, что «правило Крамера» работает только для систем с ненулевым детерминантом (определителем системы), тогда как «метод Гаусса» работает для любой системы линейных уравнений.
Огромный вклад в развитие теории матриц в середине XIX внесли такие известные ученые как Уильям Гамильтон и Артур Кэли. Наряду с ними развивали данную теорию немецкие математики Карл Вейерштрасс и Фердинанд Георг Фробениус, а также, французский математик Мари Энмон Камиль Жордан. В 1850 году Джеймс Сильвестр ввел современное понятие матрицы. Под влиянием работ этих великих ученых в математике появился новый раздел, который был назван матричной алгеброй.
Матрицы и операции над ними
Матрица – это прямоугольная таблица, представляющая собой совокупность строк и столбцов. Размерностью матрицы называется величина m×n, где m-число строк, n-число столбцов.
Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате, решение систем линейных уравнений сводится к операциям над матрицами. А множество экономических задач можно свести к системам линейных уравнений.
Операции с матрицами не слишком громоздки и не требуют чрезмерно кропотливой работы; напротив, матричную алгебру во многих случаях ценят именно за краткость, простоту и ясность. С помощью матричной алгебры можно выразить в математической форме многие задачи, как большие, так и малые, независимо от их размерности.
Основные операции с матрицами рассмотрены в Приложении.
Решение с помощью матриц экономических задач
Для наглядности перейдём к рассмотрению задач.
1. С помощью матриц удобно записывать некоторые экономические зависимости. Одним из примеров может послужить таблица распределения ресурсов по различным отраслям экономики.
Таблица: Распределение ресурсов
| Ресурсы | Промышленность | Сельское хозяйство | Торговля |
| Трудовые ресурсы | 4,8 | 6,7 | 7,1 |
| Водные ресурсы | 3,1 | 2,5 | 5,8 |
| Электроэнергия | 5,6 | 4,3 | 3,4 |
Так, например, элемент матрицы а22 = 2,5 показывает, сколько водных ресурсов потребляет сельское хозяйство, а элемент матрицы а13 = 7,1 показывает, сколько трудовых ресурсов потребляет торговля.
2. Рассмотрим такую ситуацию. Некоторая фирма занимается реализацией четырех видов товаров в трех районах. Данные об уровне продаж товаров по районам образуют матрицу.
Величина aij, которая находится в i-й строке и j-м столбце матрицы A, обозначает количество j-го товара, проданное в i-м районе. Таким образом, строки матрицы соответствуют районам, а столбцы – видам товаров. Обозначим через ci, i= 1, 2, 3, 4 цены на реализуемые товары. Они образуют матрицу-столбец.
Если хотим найти суммарный объем продаж в первом районе, то мы должны вычислить следующее выражение:
a11c1 + a12c2 + a13c3 + a14c4,
которое является скалярным произведением первой строки матрицы A на столбец цен C. И строчка, и столбец являются арифметическими 4-х мерными векторами. Про выражение (a11c1 + a12c2 + a13c3 + a14c4) говорят, что оно получено при умножении первой строки матрицы A на столбец C.
Производя такое умножение на столбец C второй и третьей строк, получаем еще две величины, которые представляют собой суммарные продажи во втором и третьем районах. Эти две величины вместе с ранее найденной величиной образуют вектор суммарных продаж.
В этом примере фактически применено действие умножения матриц.
- годовую производительность каждого предприятия по каждому виду изделий;
- годовую потребность каждого предприятия по каждому виду сырья;
- годовую сумму кредитования каждого предприятия для закупки сырья, необходимого для выпуска продукции указанных видов и количеств.
Решение. Нужно составить матрицы, характеризующие весь интересующий нас экономический спектр производства, а затем при помощи соответствующих операций над ними получить решение данной задачи.
Каждый столбец этой матрицы соответствует дневной производительности отдельного предприятия по каждому виду продукции. Следовательно, годовая производительность j-го предприятия по каждому виду продукции получается умножением j-гo столбца матрицы А на количество рабочих дней в году для этого предприятия (j = 1, 2, 3, 4, 5). Таким образом, годовая производительность каждого предприятия по каждому из изделий описывается матрицей.
Матрица затрат сырья на единицу изделия (эти показатели по условию одинаковы для всех предприятий) имеет вид
Дневной расход по типам сырья на предприятиях описывается произведением матрицы В на матрицу А:
где i-я строка соответствует номеру типа сырья, а j-й столбец — номеру предприятия согласно табл. 16.2 (i = 1, 2, 3; j = 1, 2, 3, 4, 5). Ответ на второй вопрос задачи получим по аналогии с матрицей Агод умножением столбцов матрицы ВА на соответствующие количества рабочих дней в году для предприятий — это годовая потребность каждого предприятия в каждом виде сырья:
Введем вектор стоимости сырья.
Тогда стоимость общего годового запаса сырья для каждого предприятия получается умножением вектора 
Следовательно, суммы кредитования предприятий для закупки сырья определяются соответствующими компонентами вектора 
4. Множество экономических задач можно свести к системам линейных уравнений. Для наглядного примера рассмотрим следующую задачу.
Предположим, что кривая спроса на автомобили для некоторого периода времени может быть описана уравнением
x1 = 12000 — 0,2×2,
где x1 – цена автомобиля (в долларах), а x2 – их количество.
Предполагаем также, что уравнение кривой предложения имеет вид:
Объединим уравнения в систему.
Эту систему, конечно, легко решить непосредственно, например методом подстановки. Но мы перейдем от системы к матричному уравнению.
Напрашивается решение этого уравнения в виде:
Но операции деления матриц нет. Но есть операция вычисления обратной матрицы. Подумаем, как мы решаем уравнение 5X = 7? Мы пишем, не особенно задумываясь, X = 7/5. а как записать ответ, не пользуясь делением? Это возможно: X = 5-1•7 или 7•5-1.
Обратная матрица A-1 должна обладать свойством A-1A = E, где E – единичная матрица.
Умножим слева на A-1 обе части матричного уравнения AX = В и получим равенство
Но так как A-1A =E, а EX = X, то мы приходим к равенству
Это означает, что равновесная цена на автомобили X = 4200 долларов, а объем продаж X = 39000 штук.
Подобные задачи удобно решать методом Гаусса – методом последовательного исключения переменных, который заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Преобразования Гаусса можно проводить не только с уравнениями системы, но и с матрицей их коэффициентов.
Заключение
Проанализировав применение матричной алгебры в экономике, можно прийти к выводу, что использование матриц имеет свои достоинства и недостатки.
Недостатки заключаются в том, что матричная алгебра не обеспечивает реальных рекомендаций по разработке специфических стратегий; по матрицам невозможно определить сферы бизнеса, которые готовы стать победителями.
Достоинства же применения матриц в том, что они используют широкий набор стратегически значимых переменных; указывают направление движения ресурсов; позволяют с минимальными затратами труда и времени обрабатывать огромный и весьма разнообразный статистический материал, различные исходные данные, характеризующие уровень, структуру, особенности социально-экономического комплекса.
При наличии отрицательных моментов применения матричной алгебры положительная часть значительно обширнее.
Из выше рассмотренного можно сделать вывод, что роль матриц в экономике очень и очень велика. Ведь благодаря их использованию можно гораздо быстрее, чем с использованием какого-либо другого математического аппарата, и проще решить многие экономические задачи, что чрезвычайно важно для экономистов.
Используемая литература
- Коршунова Н.И., Плясунов В.С. Математика в экономике. — М.:«Вита-Пресс», 1996.
- Сирл С., Госман У. Матричная алгебра в экономике. – М.:Статистика, 1974.
- Немцова А.В., Попова С.В. ПРИМЕНЕНИЕ СРЕДСТВ МАТРИЧНОЙ АЛГЕБРЫ ДЛЯ РЕШЕНИЯ ЗАДАЧ ЭКОНОМИЧЕСКОГО СОДЕРЖАНИЯ // Современные наукоемкие технологии. – 2014. – № 5-2.
- Ахмедханова А.И., Кожемякина В.А., Мамаев И.И. ПРИМЕНЕНИЕ МАТРИЦ В ЭКОНОМИКЕ // Международный студенческий научный вестник. – 2015. – № 3-4.;
- Авдеев Д.Д., Турченко В.В. ПРИМЕНЕНИЕ МАТРИЦ В ЭКОНОМИКЕ // Научное обозрение. Педагогические науки. – 2019. – № 4-3.
Приложение. Операции над матрицами
Линейные операции над матрицами.
Определение 1. Матрицей называется прямоугольная таблица:
A = 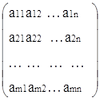
Число m ее строк и число n ее столбцов называют размерами матрицы А. Про матрицу А говорят, что она размером m×n. Обозначим Mm×n множество матриц размером m×n (m строк и n столбцов).
Определение 2. Пусть A=(aij) и B=(bij) – две матрицы размером m×n.
Суммой матриц A и B называется матрица C=(cij) є Mm×n , такая, что cij = aij+bij для всех i и j.
Действие сложения определено для матриц одинакового размера
C=A +B=
Произведением матрицы A на число α называется матрица αA с элементами (αaij).
αA=
Операции сложения матриц и умножения матрицы на число называют линейными операциями.
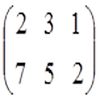
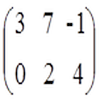
http://matica.org.ua/metodichki-i-knigi-po-matematike/osnovy-matematiki-i-ee-prilozheniia-v-ekonomicheskom-obrazovanii-krass-m-s-chuprynov-b-p/16-2-ispolzovanie-sistem-lineinykh-uravnenii
http://tvorcheskie-proekty.ru/node/3583