Эквивалентные преобразования логических выражений логические уравнения

Логика. Основные сведения.

1. Элементарные высказывания

1.1. Истинные и ложные высказывания.

Утверждения (они же: высказывания) об объектах окружающего мира строятся из элементарных высказываний. Такие высказывания утверждают что-то о свойствах объекта или об отношениях между объектами (чаще всего – между двумя объектами).

Забор красный. Здесь забор – объект, а красный описывает его свойство. «красный» (иногда говорят – свойство «быть красным»). Имеется в виду конкретный забор, а не забор вообще! В русском языке свойства часто (но не всегда) выражаются прилагательными.
Коля и Петя – друзья. Здесь Коля и Петя – «объекты», а слово друзья описывает отношение между ними. Это отношение симметрично – смысл сказанного не поменяется, если написать «Петя и Коля – друзья». Здесь, как и во всех элементарных высказываниях, имеются в виду конкретные люди.
Коля старше, чем Петя. Здесь отношение описывается словами «старше, чем». Это отношение не является симметричным.

Высказывание может быть истинным (верным) или ложным (неверным). Например, Коля может на самом деле быть старше, чем Петя (тогда высказывание 3 истинно). А, может быть, Коля младше Пети, или они одного возраста. Тогда это высказывание ложно.

1.2. Объекты, свойства и отношения в математике.

В математике мы имеем дело с математическими объектами, их свойствами и отношениями. Примеры математических объектов: числа: натуральные, целые, рациональные (они же — обыкновенные дроби), вещественные; точки, прямые, множества. С числами, точками и прямыми вы познакомились на уроках математики. Про множества коротко написано здесь.

Вот примеры свойств, отношений и высказываний для целых чисел (при описании свойств и отношений вместо чисел стоят многоточия…) .

Свойства: … — четное; … — нечетное, … — положительное.

Примеры высказываний: (1) 4 – четное. (2) 4 – нечетное. (3) 4 – положительное. Здесь первое и третье высказывание истинны, а второе – ложно.

Отношение: …больше, чем …; … меньше, чем…; … делится на … .

Примеры высказываний: (1) 4 больше, чем 2. (2) 4 меньше, чем 2. (3) 4 делится на 2. Здесь тоже первое и третье высказывание истинны, а второе – ложно.

В математике отношения часто записываются специальными знаками. Например, 6 Замечание . Вместо «явного» обозначения, например, чисел в высказываниях можно использовать и выражения, значениями которых являются числа. Пример:

(2+ 3) 1.3. Утверждения всеобщности.

В школьной (и не только 🙂 ) математике в элементарных высказываниях часто используются не только «имена» объектов (числа, множества и др.), но и переменные. Пример:

Здесь имеется в виду вот что. Для любых чисел, если их подставить вместо a и b, получится истинное высказывание. То есть, истинны все указанные ниже высказывания и еще бесконечно много подобных им высказываний:

27 + 12 = 12 + 27 (вместо a подставили 27, вместо b подставили 12)

2 + 5 = 5 + 2 (вместо a подставили 2, вместо b подставили 5)

5 + 2 = 2 + 5 (вместо a подставили 5, вместо b подставили 2)

5 + 5 = 5 + 5 (вместо a подставили 5, вместо b тоже подставили 5)

Истинность утверждений о всеобщности нельзя проверить непосредственно! Их нужно доказывать (или принимать в качестве аксиом).

2. Логические значения, логические связки и логические высказывания

2.1. Составные высказывания

Из элементарных высказываний можно строить более сложные (составные) высказывания, используя связки И, ИЛИ, НЕ.

Примеры. Забор красный И забор деревянный.

Коля старше, чем Петя ИЛИ Коля старше, чем Федя

Смысл этих высказываний понятен.

Высказывание с И содержит два элементарных высказывания. Составное высказывание с И истинно тогда и только тогда, когда истинны оба эти элементарные высказывания. Если хоть одно из них ложно, — составное высказывание ложно.

Высказывание с ИЛИ тоже содержит два элементарных высказывания. Составное высказывание с ИЛИ истинно тогда и только тогда, когда истинно хотя бы одно из этих элементарных высказываний. Если оба эти высказывания ложны, — составное высказывание ложно.

Высказывание с НЕ содержит одно элементарное высказывание (в русском языке НЕ часто ставится в середину этого высказывания). Составное высказывание с НЕ истинно, если исходное элементарное высказывание ложно и, наоборот, если исходное высказывание истинно, то составное высказывание с НЕ ложно.

Составные высказывания можно строить не только из элементарных высказываний, но и из других составных высказываний. В этом построение составных высказываний похоже на построение алгебраических выражений. Например, понятно, что означает такое высказывание (хотя оно написано не на русском языке, а с использованием скобок : )

(Коля старше, чем Петя ИЛИ Коля старше, чем Федя) И (Коля НЕ старше, чем Ваня)

Здесь 3 элементарных высказывания.

2.2. Логические значения. Логические операции.

Мы уже знаем, что каждому высказыванию можно приписать одно из двух логических значений – истина (часто обозначается: 1) или ложь (часто обозначается: 0). Слова И, ИЛИ, НЕ задают операции над логическими значениями (логические операции). Действительно, например, составное высказывание с И истинно тогда и только тогда, когда истинны оба его элементарные высказывания. Если хоть одно из них ложно, — составное высказывание ложно. Здесь нам не важно, каковы были исходные высказывания. Истинность составного высказывания зависит только от логического (иногда говорят — истинностного) значения исходных высказываний.

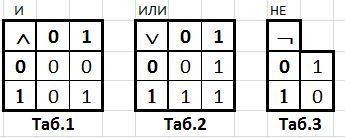
Так как логических значений всего два, то эти операции можно описать таблицами.

У операций И, ИЛИ, НЕ есть «научные» названия (даже несколько для каждой операции 🙂 и специальные обозначения (в примерах A, B обозначают какие-то конкретные логические значения):

НЕ: отрицание, инверсия. Обозначение: ¬ (например, ¬А);

И: конъюнкция, логическое умножение.

Обозначается /\ (например, А /\ В) либо & (например, А & В);

ИЛИ: дизъюнкция, логическое сложение.

Обозначается \/ (например, А \/ В).

В математике используются и другие логические операции.

Каждая логическая операция может быть задана своей таблицей. Вот еще два примера логических операций:

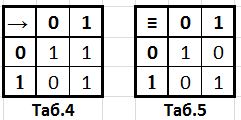
1) следование (импликация); обозначается → (например, А → В). Выражение А → В истинно если A ложно ИЛИ B истинно. То есть, А → В означает то же самое, что и (¬А) \/ В. См. таб. 4.

2) тождество (эквивалетность); обозначается ≡ (например, A ≡ B). Выражение A ≡ B истинно тогда и только тогда, когда значения A и B совпадают (либо они оба истинны, либо они оба ложны). См. таб. 5.

Логические операции играют для логических значений ту же роль, что и арифметические операции для чисел. Аналогично построению алгебраических выражений, с помощью логических операций можно строить логические выражения. Как и алгебраические выражения, логические выражения могут включать константы (логические значений 1 и 0) и переменные. Если в логическом значении есть переменные, оно задает функцию (логическую функцию; синоним: булеву функцию). Значение такой функции при заданном наборе значений аргументов вычисляется подстановкой этих значений в выражение вместо переменных.

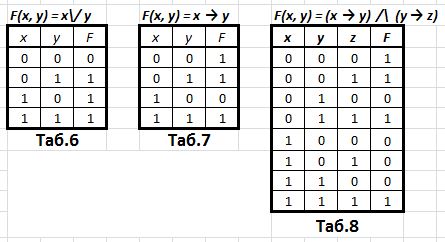
Для каждого логического выражения можно составить таблицу истинности, которая описывает, какое значение принимает соответствующая логическая функция (синоним: принимает выражение) при каждом допустимом наборе значений переменных. Каждая строка таблицы истинности соответствует одному возможному набору аргументов логической функции. Поэтому таблица истинности для логической функции от n переменных содержит 2 n строк. В каждой строке таблицы истинности указывается набор значений переменных и значение функции, соответствующее этому набору. Вот таблицы истинности для выражений x \/ y (таблица 6), x → y (таблица 7) и (x → y) /\ (y → z) (таблица 8).

2.4. Приоритеты логических операций.

При записи логических выражений, как и при записи алгебраических выражений, иногда можно не писать скобки При этом соблюдаются следующие договоренности о старшинстве (приоритете) логических операций, первыми указаны операции, которые выполняются в первую очередь:

конъюнкция (логическое умножение),

дизъюнкция (логическое сложение),

Таким образом, ¬А \/ В \/ С \/ D означает то же, что и ((¬А) \/ В)\/ (С \/ D).

Возможна запись А \/ В \/ С вместо (А \/ В) \/ С. То же относится и к конъюнкции: возможна запись А /\ В /\ С вместо (А /\ В) /\ С.

3. Свойства логических выражений и таблиц истинности.

Приведенный ниже список НЕ претендует на полноту, но, надеемся, достаточно представителен.

3.1. Общие свойства

1) Для n логических переменных существует ровно 2 n различных наборов значений.

2) Таблица истинности для логического выражения от n переменных содержит n+1 столбец (по одному столбцу на каждую переменную + 1 столбец на значение выражения) и 2 n строк (по одной строке на каждый набор значений переменных).

1) Если хоть одно из выражений, к которым применяется дизъюнкция, истинно на некотором наборе значений переменных, то и вся дизъюнкция истинна для этого набора значений.

2) Если все выражения из некоторого списка ложны на некотором наборе значений переменных, то дизъюнкция этих выражений тоже ложна.

3) Значение дизъюнкции не зависит от порядка записи выражений, к которым она применяется.

4) При вычислении дизъюнкции выражений эти выражения можно группировать как угодно — значение дизъюнкции не изменится.

5) Пусть все выражения, к которым применяется дизъюнкция, — это различные переменные или их отрицания. Тогда существует ровно один набор значений переменных, при которых дизъюнкция ложна. Переменная в этом наборе имеет значение 1, если в дизъюнкцию она входит с отрицанием и значение 0 в противном случае.

1) Если хоть одно из выражений, к которым применяется конъюнкция, ложно на некотором наборе значений переменных, то и вся конъюнкция ложна для этого набора значений.

2) Если все выражения из некоторого списка истинны на некотором наборе значений переменных, то конъюнкция этих выражений тоже истинна.

3) Значение конъюнкции не зависит от порядка записи выражений, к которым она применяется.

4) При вычислении конъюнкции выражений эти выражения можно группировать как угодно — значение конъюнкции не изменится.

5) Пусть все выражения, к которым применяется конъюнкция, — это различные переменные или их отрицания. Тогда существует ровно один набор значений переменных, при которых конъюнкция истинна. Переменная в этом наборе имеет значение 1, если в конъюнкцию она входит без отрицания и значение 0 в противном случае.

1) Импликация A →B равносильна дизъюнкции (¬А) \/ В. Эту дизъюнкцию можно записать и так: ¬А \/ В.

2) Импликация A →B принимает значение 0 (ложь) только если A=1 и B=0. Если A=0, то импликация A→B истинна при любом значении B. Если B=1, то импликация A→B истинна при любом значении A.

1) Эквивалентность A ≡ B равносильна конъюнкции двух импликаций: A→B и B→A. Эту конъюнкцию можно записать так: (A→B)/\ (B→A)

2) Эквивалентность A ≡ B принимает значение 1 (истина) тогда и только тогда, когда значения переменных A и B одинаковы, т.е. A=B=1 или A=B=0.

Поэтому эквивалентность A ≡ B равносильна выражению (A/\B) \/ ((¬А) /\ (¬В) ).

3) Эквивалентность A ≡ B принимает значение 0 (ложь) тогда и только тогда, когда значения переменных A и B различны, т.е. A=0, а B=1 или A=1, а B=0. Поэтому эквивалентность A ≡ B равносильна выражению ¬ ( (A/\¬B) \/ (А /\¬В) )

3.6. Построение выражения с заданной таблицей истинности

Для любого множества наборов значений переменных можно построить выражение, которое истинно на всех наборах из заданного множества и только на них. Это выражение удобно записать в виде дизъюнкции конъюнкций, причем в каждой конъюнкции (а) каждый член – это простая переменная или ее отрицание и при этом (б) содержатся все переменные.

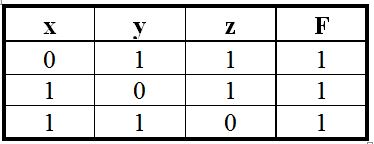
Тогда функция F может быть задана таким выражением:

Здесь первый член дизъюнкции соответствует первой строке таблицы фрагмента истинности; второй член – второй строке; третий член – третьей строке.

Таким образом, для любой таблицы истинности можно построить логическое выражение с данной таблицей истинности.

4. Эквивалентные преобразования логических выражений

4.1. Эквивалентные выражения.

Два логических выражения, содержащих переменные, называются равносильными (эквивалентными), если значения этих выражений совпадают при любых значениях переменных. Так, выражения А → В и (¬А) \/ В равносильны, а А/\В и А \/ В – нет (значения выражений разные, например, при А = 1, В = 0).

Эквивалентные выражения имеют одинаковые таблицы истинности, а у неэквивалентных выражений таблицы истинности различны.

Понятие эквивалентности для логических выражений полностью аналогично понятию эквивалентности для алгебраических выражений.

4.2. Эквивалентные (тождественные) преобразования выражений.

Выяснить, эквивалентны ли два выражения, можно сравнив их таблицы истинности. Но это не всегда удобно: построение таблицы истинности — громоздкая задача. Кроме того, часто нужно не просто проверить, эквивалентны ли два данных логических выражения, а построить для данного выражения эквивалентное ему выражение, имеющее заданный вид. Например, бывает удобно представить выражение в виде дизъюнкции или в виде импликации (см. здесь). Аналогия для алгебраических выражений: разложить на множители выражение x 2 -y 2 (ответ: (x-y)*(x+y) ).

Замена выражения на другое выражение, эквивалентное ему, называется эквивалентным (синоним: тождественным) преобразованием.

Основное правило тождественных преобразование — это правило подстановки: если в выражении A заменить подвыражение P на эквивалентное ему выражение Q, то полученное новое выражение B будет эквивалентно исходному выражению A.

Правило подстановки работает и для логических, и для алгебраических выражений.

Пример 1. Рассмотрим выражение A = (x→y)∨z . Заменим подвыражение P = x→y на эквивалентное ему по определению выражение Q = ¬x∨y. Заменяем в A выражение P выражением Q. Получим выражение B = (¬x∨y)∨z. Выражение B эквивалентно выражению A. Учитывая приоритеты выполнения логических операций, выражение B можно записать и так: ¬x∨y∨z.

4.3. Основные логические тождества.

Между решением задач на эквивалентное преобразование логических и алгебраических выражений есть существенная разница. В алгебре есть устоявшийся список тождественных преобразований выражений. В него входят формулы, связанные с определением степени и основными законами сложения и умножения (сочетательный, переместительный, распределительный), а также так называемые формулы сокращенного умножения (квадраты и кубы суммы и разности; разность квадратов, сумма и разность кубов). В курсе логики такого общепринятого списка нет.

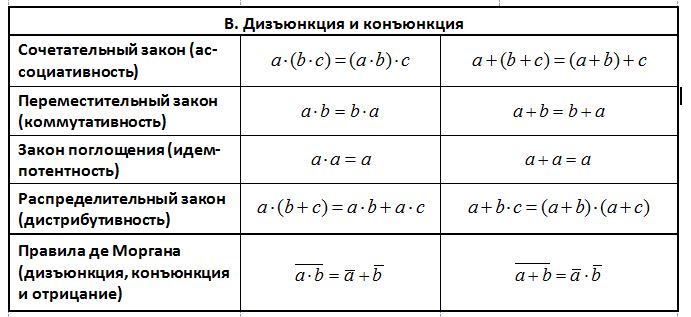
В таблице 1 приведен набор логических тождеств (пар эквивалентных логических выражений), которые полезно знать, сдавая ЕГЭ. Это не значит, что другие элементарные тождества вам не понадобится. Мы просто надеемся, что вы сможете при необходимости вывести другие понадобившиеся тождества. Желательно уметь пользоваться этими формулами так же свободно, как, например, алгебраическими формулами сокращенного умножения. Деление формул в таблице на группы – условное и приведено лишь для удобства восприятия.

Примечание. В таблицах использована «алгебро-подобная» система обозначений логических операций. Конъюнкция (логическое умножение) и дизъюнкция (логическое сложение) обозначаются символами «·» и «+» соответственно, а отрицание – чертой сверху. Эти обозначения общеприняты среди инженеров (но не специалистов по математической логике :)) и используются в некоторых школьных учебниках, в частности, в учебниках К.Ю.Полякова и Е.А.Еремина

5. Высказывания о множествах

Логические выражения над элементарными высказываниями о множествах (высказывания вида «A=∅», «x∈A» «A⊆B» ) можно преобразовывать, используя не только общие правила преобразования логических выражений, но и свои правила, связанные со свойствами операций над множествами. Ниже U — это универсальное множество; x — его произвольный элемент, A, B, X — множества. Верны следующие утверждения.

1. Следующие высказывания эквивалентны, т.е. имеют одинаковые логические значения при любых x, A, B (это обозначено знаком ⇔)

2. Следующие высказывания эквивалентны, т.е. имеют одинаковые логические значения при любых X, A, B (это обозначено знаком ⇔)

3. (а) Пусть A ⊆ B, т.е. A — подмножество B; x — элемент универсального множества U. Тогда истинно высказывание:

(б) Пусть высказывание (x ∈ A) → (x∈ B) истинно при любом x ∈ U. Тогда A ⊆ B.

4. (а) Пусть A ⊆ B, т.е. A — подмножество B; X ⊆ U — произвольное множества. Тогда истинно высказывание:

(б) Пусть высказывание (X∩A ≠Ø ) → (X∩B ≠Ø ) истинно для любого множества X ⊆ U. Тогда A ⊆ B.

5. Следующее высказывания истинны для любых множеств A, B, X

6. Примеры эквивалентных преобразований

Первые два примера содержат доказательства свойств импликации из таблицы 1С (см. п.4).

Пример 1 . Преобразуем выражение (¬y)→ (¬x) в выражение x→ y. Имеем:

1) (¬y) ∨ (¬(¬x) ) — замена импликации дизъюнкцией

3) x → y — замена дизъюнкции импликацией

Пример 2 . Преобразуем выражение x → (y→ z) в выражение (x∧y)→ z. Имеем:

При анализе высказываний о множествах бывает удобно преобразовывать выражения к импликации, у которой и левый, и правый члены импликации не содержат. Рассмотрим такие примеры.

Информатика. 10 класс

Конспект урока

Информатика, 10 класс. Урок № 12.

Тема — Преобразование логических выражений

Перечень вопросов, рассматриваемых в теме: основные законы алгебры логики, преобразование логических выражений, логические функции, построение логического выражения с данной таблицей истинности и его упрощение, дизъюнктивная и конъюнктивная нормальная форма, совершенная дизъюнктивная нормальная форма (СДНФ), совершенная конъюнктивная нормальная форма (СКНФ).

Глоссарий по теме: основные законы алгебры логики, логические функции, дизъюнктивная и конъюнктивная нормальная форма, совершенная дизъюнктивная нормальная форма (СДНФ), совершенная конъюнктивная нормальная форма (СКНФ)

Основная литература по теме урока:

Л. Л. Босова, А. Ю. Босова. Информатика. Базовый уровень: учебник для 10 класса

— М.: БИНОМ. Лаборатория знаний, 2017 (с.197—209)

Открытые электронные ресурсы по теме:

Теоретический материал для самостоятельного изучения.

Способ определения истинности логического выражения путем построения его таблицы истинности становится неудобным при увеличении количества логических переменных, т.к. за счет существенного увеличения числа строк таблицы становятся громоздкими. В таких случаях выполняются преобразования логических выражений в равносильные. Для этого используют свойства логических операций, которые иначе называют законами алгебры логики.

Основные законы алгебры логики

Справедливость законов можно доказать построением таблиц истинности.

Пример 1. Упростим логическое выражение

Последовательно применим дистрибутивный закон и закон исключенного третьего:

В общем случае можно предложить следующую последовательность действий:

Заменить операции строгая дизъюнкция, импликация, эквиваленция на их выражения через операции конъюнкция, дизъюнкция, инверсия;
Раскрыть отрицания сложных выражений по законам де Моргана.
Используя законы алгебры логики, упростить выражение.

Пример 2. Упростим логическое выражение .

Здесь последовательно использованы замена операции импликация, закон де Моргана, распределительный закон, закон противоречия и операция с константой, закон идемпотентности и поглощения.

Аналогичные законы выполняются для операции объединения, пересечения и дополнения множеств. Например:

Пример 3. На числовой прямой даны отрезки B = [2;12] и C = [7;18]. Каким должен быть отрезок A, чтобы предикат становился истинным высказыванием при любых значениях x.

Преобразуем исходное выражение, избавившись от импликации:

A, B, C — множества. Для них можно записать (U — универсальное множество).

Будем считать, что.

Тогда , причем это минимально возможное множество А.

Так как множество B — это отрезок [2;12], а множество — это промежутки и, то пересечением этих множеств будет служить промежуток . В качестве ответа мы можем взять этот промежуток, а также любой другой, его включающий.

Пример 4. Для какого наименьшего неотрицательного целого десятичного числа а выражение

тождественно истинно (т. е. принимает значение 1 при любом неотрицательном целом значении десятичной переменной х)? Здесь & — поразрядная конъюнкция двух неотрицательных целых десятичных чисел.

Перепишем исходное выражение в наших обозначениях и преобразуем его:

Рассмотрим предикат . В числе 28₁₀=11100₂ 4-й, 3-й и 2-й биты содержат единицы, а 1-й и 0-й — нули. Следовательно, множеством истинности этого предиката являются такие числа х, у которых хотя бы один из битов с номерами 4, 3 или 2 содержит единицу. Если и 4-й, и 3-й, и 2-й биты числа х нулевые, то высказывание будет ложным.

Рассмотрим предикат . В числе 45₁₀=101101₂ 5-й, 3-й, 2-й и 0-й биты содержат единицы, 4-й и 1-й — нули. Следовательно, множеством истинности этого предиката являются такие числа х, у которых хотя бы один из битов с номерами 5, 3, 2 или 0 содержит единицу. Если и 5-й, и 3-й, и 2-й, и 0-й биты числа х нулевые, то высказывание будет ложным.

Рассмотрим предикат . В числе 17₁₀=10001₂ 3-й, 2-й и 1-й биты содержат нули, 4-й и 0-й — единицы. Побитовая конъюнкция 17 и х будет равна 0, если в числе х 4-й и 0-й биты будут содержать нули. Множество истинности этого предиката — все х с нулями в 4-м и 0-м битах.

По условию задачи надо, чтобы .

Запишем это выражение для рассмотренных множеств истинности:

Так как , примем .

Объединением множеств M и N являются все двоичные числа, у которых хотя бы один из битов с номерами 5, 4, 3, 2, 0 содержит единицу. Пересечением этого множества с множеством K будут все двоичные числа, у которых биты с номерами 4 и 0 будут заняты нулями, т.е. такие двоичные числа, у которых хотя бы один из битов с номерами 5, 3, 2 содержит 1. Все эти числа образуют множество А.

Искомое число a должно быть таким, чтобы при любом неотрицательном целом значении переменной х: , и, кроме того, оно должно быть минимальным из возможных. Этим условиям удовлетворяет число 101100₂ = 44₁₀.

Значение любого логического выражения определяется значениями входящих в него логических переменных. Тем самым логическое выражение может рассматриваться как способ задания логической функции.

Совокупность значений n аргументов удобно интерпретировать как строку нулей и единиц длины n. Существует ровно различных двоичных строк длины n. Так как на каждой такой строке некая функция может принимать значение 0 или 1, общее количество различных булевых функций от n аргументов равно .

Для n=2 существует 16 различных логических функций. Рассмотрим их подробнее.

Учитель информатики

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

Преобразование логических выражений

Информатика. 10 класса. Босова Л.Л. Оглавление

§ 20. Преобразование логических выражений

Способ определения истинности логического выражения путём построения его таблицы истинности становится неудобным при увеличении количества логических переменных, т. к. за счёт существенного увеличения числа строк таблицы становятся громоздкими. В таких случаях выполняются преобразования логических выражений в равносильные. Для этого используют свойства логических операций, которые иначе называют законами алгебры логики.

20.1. Основные законы алгебры логики.

Приведём основные законы алгебры логики.

1. Переместительные (коммутативные) законы:

2. Сочетательные (ассоциативные) законы:

(A v В) v С = A v (В v С).

3. Распределительные (дистрибутивные) законы:

A v (В & С) = (A v В) & (A v С).

4. Законы идемпотентности (отсутствия степеней и коэффициентов):

5. Закон противоречия:

6. Закон исключённого третьего:

7. Закон двойного отрицания:

8. Законы работы с константами:

A v 1 = 1; A v O = A;

9. Законы де Моргана:

10. Законы поглощения:

Справедливость законов можно доказать построением таблиц истинности.

Пример 1. Упростим логическое выражение

Последовательно применим дистрибутивный закон и закон исключённого третьего:

Пример 2. Упростим логическое выражение

Аналогичные законы выполняются для операций объединения, пересечения и дополнения множеств. Например:

Пробуйте самостоятельно доказать один из этих законов с помощью кругов Эйлера.

Пример 3. На числовой прямой даны отрезки В = [2; 12] и С = [7; 18]. Каким должен быть отрезок А, чтобы предикат

становился истинным высказыванием при любых значениях х.

Преобразуем исходное выражение, избавившись от импликации:

причём это минимально возможное множество А.

Множество В — это отрезок [2; 12].

Изобразим это графически:

Пересечением этих множеств будет служить промежуток [2; 7[. В качестве ответа мы можем взять этот промежуток, а также любой другой, его включающий.

Чему равна минимальная длина отрезка А? Укажите ещё несколько вариантов множества А.

Пример 4. Для какого наименьшего неотрицательного целого десятичного числа а выражение

Прежде всего, вспомним, что представляет собой поразрядная конъюнкция двух целых десятичных чисел, например 27 и 22.

Обратите внимание на то, что если в некотором бите хотя бы одного сомножителя есть 0, то 0 есть и в этом бите результата, а 1 в результате получается только тогда, когда в соответствующих битах каждого сомножителя есть 1.

Перепишем исходное выражение в наших обозначениях:

Рассмотрим предикат М(х) = (х & 28 ? 0). В числе 28 = 11100₂ 4-й, 3-й и 2-й биты содержат единицы, а 1-й и 0-й — нули. Следовательно, множеством истинности этого предиката являются такие числа х, у которых хотя бы один из битов с номерами 4, 3 или 2 содержит единицу. Если и 4-й, и 3-й, и 2-й биты числа х нулевые, то высказывание х & 28 ? 0 будет ложным.

Рассмотрим предикат N(x) = (х & 45 ? 0). В числе 45 = 101101₂ 5-й, 3-й, 2-й и 0-й биты содержат единицы, 4-й и 1-й — нули.

Следовательно, множеством истинности этого предиката являются такие числа х, у которых хотя бы один из битов с номерами 5, 3, 2 или 0 содержит единицу. Если и 5-й, и 3-й, и 2-й, и 0-й биты числа х нулевые, то высказывание х & 45 ? 0 будет ложным.

Рассмотрим предикат К(х) = (х & 17 = 0). В числе 17 = 10001₂ 3-й, 2-й и 1-й биты содержат нули, 4-й и 0-й — единицы. Побитовая конъюнкция 17 и х будет равна нулю, если в числе х 4-й и 0-й биты будут содержать нули. Множество истинности этого предиката — все х с нулями в 4-м и 0-м битах.

По условию задачи надо, чтобы

Запишем это выражение для рассмотренных множеств истинности:

Объединением множеств М и N являются все двоичные числа, у которых хотя бы один из битов с номерами 5, 4, 3, 2, 0 содержит единицу. Пересечением этого множества с множеством К будут все двоичные числа, у которых биты с номерами 4 и 0 будут заняты нулями, т. е. такие двоичные числа, у которых хотя бы один из битов с номерами 5, 3, 2 содержит 1. Все эти числа образуют множество А.

Искомое число а должно быть таким, чтобы при любом неотрицательном целом значении переменной х: х & а ? 0, и кроме того, оно должно быть минимальным из возможных. Этим условиям удовлетворяет число 101100₂. Действительно, единицы в нём стоят в тех и только в тех битах, которые нужны для выполнения условия х & а ? 0.

Итак, требуемое число 101100₂ или 44₁₀.

Приведите пример такого десятичного числа а, что для него х & а ? 0 при любом неотрицательном целом значении десятичной переменной х, но само число а не является минимально возможным.

Пример 5. Выясним, сколько решений имеет следующая система из двух уравнений:

Конъюнкция истинна тогда и только тогда, когда истинны все образующие её высказывания. Следовательно, каждая из трёх входящих в конъюнкцию импликаций должна быть равна 1.

Начнем строить дерево решений, представив на нём значения переменных х₁ и х₂ при которых х₁ ? х₂ = 1.

Продолжим строить дерево решений. Значения переменной х₃ будем выбирать такими, чтобы при имеющихся х₂ импликация х₂ ? х₃ оставалась истинной.

То же самое проделаем для переменной х₄.

На дереве видно, что рассматриваемое нами уравнение имеет 5 решений — 5 разных наборов значений логических переменных x₁, х₂, х₃, х₄, при которых выполняется равенство:

Следовательно, как и первое уравнение, это уравнение имеет 5 решений. Представим их в табличной форме:

Решение исходной системы логических уравнений — это множество различных наборов значений логических переменных х₁, х₂, х₃, х₄, у₁, у₂, у₃, у₄ таких, что при подстановке каждого из них в систему оба уравнения превращаются в истинные равенства.

Начнём строить такие наборы или двоичные цепочки. Их началом может служить любой из пяти наборов — решений первого уравнения, а концом — любой из пяти наборов — решений второго уравнения. Например, на основе одного из решений первого уравнения можно построить следующие пять решений системы:

Всего мы можем построить 5 • 5 = 25 решений системы.

Вспомните, как называется теорема комбинаторики, которую мы применили для подсчёта количества решений системы.

20.2. Логические функции

Значение любого логического выражения определяется значениями входящих в него логических переменных. Тем самым логическое выражение может рассматриваться как способ задания логической функции.

Совокупность значений п аргументов удобно интерпретировать как строку нулей и единиц длины n. Существует ровно 2 n различных двоичных строк длины n. Так как на каждой такой строке некая функция может принимать значение 0 или 1, общее количество различных булевых функций от n аргументов равно

Для n = 2 существует 16 различных логических функций.

Рассмотрим их подробнее.

С увеличением числа аргументов количество логических функций резко возрастает. Так, для трёх переменных существует 256 различных логических функций! Но изучать их все нет никакой необходимости. Дело в том, что путём преобразований функция любого количества переменных может быть выражена через функции только двух переменных. Более того, можно использовать не все, а лишь некоторые логические функции двух переменных. Например:

1) F₂ и F₁₁ (конъюнкция и отрицание второго аргумента);

2) F₈ и F₁₃ (дизъюнкция и отрицание первого аргумента);

3) F₉ (стрелка Пирса, отрицание дизъюнкции);

4) F₁₅ (штрих Шеффера, отрицание конъюнкции).

Два последних примера говорят о том, что при желании всю алгебру логики можно свести к одной функции! Но чаще всего логические функции записываются в виде логического выражения через отрицание, конъюнкцию и дизъюнкцию.

20.3. Составление логического выражения по таблице истинности и его упрощение

Ранее мы выяснили, что для любого логического выражения можно составить таблицу истинности. Справедливо и обратное: для всякой таблицы истинности можно составить соответствующее ей логическое выражение.

Алгоритм составления логического выражения по таблице истинности достаточно прост. Для этого надо:

1) отметить в таблице истинности наборы переменных, при которых значение логического выражения равно единице;
2) для каждого отмеченного набора записать конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае — её отрицание;
3) все полученные конъюнкции связать операциями дизъюнкции.

Пример 6. Имеется следующая таблица истинности:

После выполнения двух первых шагов алгоритма получим:

После выполнения третьего шага получаем логическое выражение:

Попробуем упростить полученное логическое выражение. Прежде всего, вынесем за скобки В — общий сомножитель, имеющийся у всех трёх слагаемых, затем — сомножитель

, а далее используем законы алгебры логики.

САМОЕ ГЛАВНОЕ

Логическая функция может быть задана с помощью таблицы истинности или аналитически, т. е. с помощью логического выражения.

Для всякой таблицы истинности можно составить соответствующее ей логическое выражение.

Вопросы и задания

Известно, что выражение

истинно при любом значении переменной х. Определите наименьшее возможное количество элементов множества А.

истинно при любом значении переменной х.