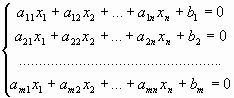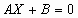Метод Гаусса онлайн
Данный онлайн калькулятор находит решение системы линейных уравнений (СЛУ) методом Гаусса. Дается подробное решение. Для вычисления выбирайте количество переменных и количество уравнений. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить.»
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Метод Гаусса
Метод Гаусса − это метод перехода от исходной системы линейных уравнений (при помощи эквивалентных преобразований) к системе, которая решается проще, чем исходная система.
Эквивалентными преобразованиями системы линейных уравнений являются:
- перемена местами двух уравнений в системе,
- умножение какого-либо уравнения в системе на ненулевое действительное число,
- прибавление к одному уравнению другого уравнения, умноженного на произвольное число.
Рассмотрим систему линейных уравнений:
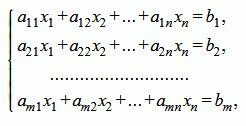 | (1) |
Запишем систему (1) в матричном виде:
| Ax=b | (2) |
  | (3) |
A-называется матрица коэффициентов системы, b − правая часть ограничений, x− вектор переменных, которую нужно найти. Пусть rang(A)=p.
Эквивалентные преобразования не меняют ранг матрицы коэффициентов и ранг расширеннной матрицы системы. Не меняется также множество решений системы при эквивалентных преобразованиях. Суть метода Гаусса заключается в приведении матрцы коэффициентов A к диагональному или ступенчатому.
Построим расшренную матрицу системы:
 | (4) |
Предположим a11≠0. Если это не так, то можно поменять местами эту строку со строкой с ненулевым элементом в столбце 1 (если нет таких строк, то переходим к следующему столбцу). Обнуляем все элементы столбца 1 ниже ведущего элемента a11. Для этого сложим строки 2,3, . m со строкой 1, умноженной на −a21/a11, −a31/a11, . −am1/a11, соответственно. Тогда (4) примет следующий вид:
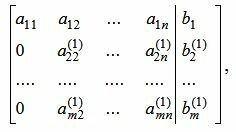 | (5) |
На следующем этапе обнуляем все элементы столбца 2, ниже элемента 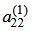
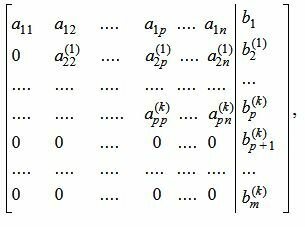 | (6) |
Обратим внимание на последние строки. Если 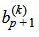

Пусть 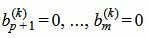
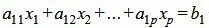 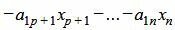 |
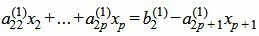  | (7) |
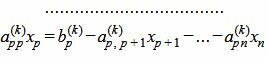 |
Так как rangA=rang(A|b), то множество решений (7) есть (n−p)− многообразие. Следовательно n−p неизвестных 
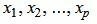
Примеры решения системы линейных уравнений методом Гаусса
Пример 1. Найти общее решение системы линейных уравнений методом Гаусса:
 |
Матричный вид записи: Ax=b, где
 |
Для решения системы, запишем расширенную матрицу:
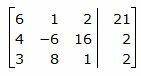 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строки 2,3 со строкой 1, умноженной на -2/3,-1/2 соответственно:
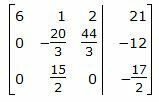 |
Исключим элементы 2-го столбца матрицы ниже элемента a2 2. Для этого сложим строку 3 со строкой 2, умноженной на 9/8:
 |
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
 |
Из вышеизложенной таблицы можно записать:
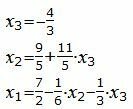 |
Подставив верхние выражения в нижние, получим решение.
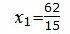 , ,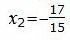 , ,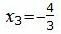 . . |
Пример 2. Найти общее решение системы линейных уравнений методом Гаусса:
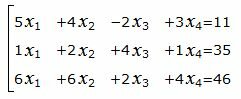 |
Матричный вид записи: Ax=b, где
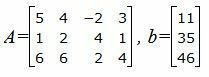 |
Для решения системы, построим расширенную матрицу:
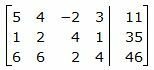 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/5,-6/5 соответственно:
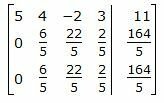 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 3 со строкой 2, умноженной на -1:
 |
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
 |
Выразим переменные x1, x2 относительно остальных переменных.
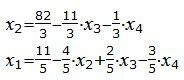 |
где x3, x4− произвольные действительные числа.
Подставив верхние выражения в нижние, получим решение.
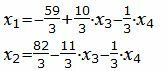 |
где x3, x4− произвольные действительные числа.
Векторный вариант решения:
Запишем вышеизложенное решение, представив свободные переменные в виде тождеств:
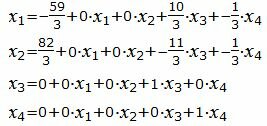 |
Тогда векторное решение можно представить так:
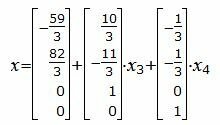 |
где x3, x4− произвольные действительные числа.
Эквивалентные системы линейных уравнений
Две системы линейных уравнений от одного набора x1. xn неизвестных и соответственно из m и p уравнений
называются эквивалентными, если их множества решений 


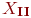





Элементарные преобразования систем линейных уравнений (строк матриц)
Определение 3.4.1 (элементарное преобразование 1-го типа). При 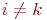

т. е. в новом i -м уравнении aij’=aij+cakj, bi’=bi+cbk.
Определение 3.4.2 (элементарное преобразование 2-го типа). При 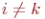
| 53. Метод Гаусса решения систем линейных уравнений | |||||||||||||
Формулы Крамера и матричный метод решения систем линейных уравнений не имеют серьезного практического применения, так как связаны с громоздкими выкладками. Практически для решения систем линейных уравнений чаще всего применяется метод Гаусса, состоящий в последовательном исключении неизвестных по следующей схеме. Для того чтобы решить систему уравнений выписывают расширенную матрицу этой системы 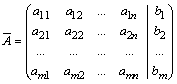 и над строками этой матрицы производят элементарные преобразования, приводя ее к виду, когда ниже главной диагонали, содержащей элементы и над строками этой матрицы производят элементарные преобразования, приводя ее к виду, когда ниже главной диагонали, содержащей элементы  будут располагаться нули. Разрешается: 1) изменять порядок строк матрицы, что соответствует изменению порядка уравнений; 2) умножать строки на любые отличные от нуля числа, что соответствует умножению соответствующих уравнений на эти числа; 3) прибавлять к любой строке матрицы другую, умноженную на отличное от нуля число, что соответствует прибавлению к одному уравнению системы другого, умноженного на число. С помощью этих преобразований каждый раз получается расширенная матрица новой системы, равносильной исходной, т. е. такой системы, решение которой совпадает с решением исходной системы. Рассмотрим метод Гаусса на примерах. Пример 14. Установить совместность и решить систему будут располагаться нули. Разрешается: 1) изменять порядок строк матрицы, что соответствует изменению порядка уравнений; 2) умножать строки на любые отличные от нуля числа, что соответствует умножению соответствующих уравнений на эти числа; 3) прибавлять к любой строке матрицы другую, умноженную на отличное от нуля число, что соответствует прибавлению к одному уравнению системы другого, умноженного на число. С помощью этих преобразований каждый раз получается расширенная матрица новой системы, равносильной исходной, т. е. такой системы, решение которой совпадает с решением исходной системы. Рассмотрим метод Гаусса на примерах. Пример 14. Установить совместность и решить систему 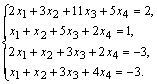 Решение. Выпишем расширенную матрицу системы и поменяем местами первую и вторую строки для того, чтобы элемент Решение. Выпишем расширенную матрицу системы и поменяем местами первую и вторую строки для того, чтобы элемент 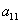 равнялся единице (так удобнее производить преобразования матрицы). равнялся единице (так удобнее производить преобразования матрицы). 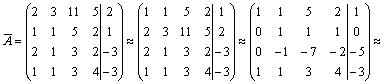  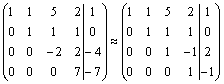 . Имеем . Имеем  Ранги матрицы системы и ее расширенной матрицы совпали с числом неизвестных. Согласно теореме Кронекера-Капелли система уравнений совместна и решение ее единственно. Выпишем систему уравнений, расширенную матрицу которой мы получили в результате преобразований: Ранги матрицы системы и ее расширенной матрицы совпали с числом неизвестных. Согласно теореме Кронекера-Капелли система уравнений совместна и решение ее единственно. Выпишем систему уравнений, расширенную матрицу которой мы получили в результате преобразований:  Итак, имеем Итак, имеем  Далее, подставляя Далее, подставляя  в третье уравнение, найдем в третье уравнение, найдем  Подставляя Подставляя  и и 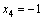 во второе уравнение, получим во второе уравнение, получим  и, наконец, подставляя в первое уравнение найденные и, наконец, подставляя в первое уравнение найденные  получим получим  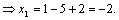 Таким образом, имеем решение системы Таким образом, имеем решение системы  54. Однородные системы линейных уравнений Однородной системой m линейных уравнений с n неизвестными называется система вида 54. Однородные системы линейных уравнений Однородной системой m линейных уравнений с n неизвестными называется система вида
Эта система может быть записана в виде матричного уравнения и операторного уравнения
Система (1) всегда совместна, так как: имеет очевидное решение x10 = x20 = … = xn0 = 0 , которое называется нулевым, или тривиальным; добавление нулевого столбца не меняет ранга матрицы, следовательно, выполняется достаточное условие теоремы Кронекера–Капелли; θ О Img ^A , так как Img ^A — линейное пространство. Естественно, нас интересуют нетривиальные решения однородной системы. Условие нетривиальной совместности: Для того, чтобы однородная система имела нетривиальное решение, необходимо и достаточно, чтобы ранг ее основной матрицы был меньше числа неизвестных. Доказательство см. в книге О.В. Зиминой «Линейная алгебра и аналитическая геометрия», стр. 77. Следствие. Для того, чтобы однородная система n линейных уравнений с n неизвестными (матрица системы A — квадратная) имела нетривиальное решение, необходимо и достаточно, чтобы определитель матрицы этой системы был равен нулю ( det A = 0 ). Общим решением системы линейных уравнений называется формула, которая определяет любое ее решение. Так как система (1) эквивалентна операторному уравнению (2), то множество всех ее решений есть ядро оператора ^A . Пусть Ker ^A ≠ θ , Rg ^A = r и x1, x2, … , xn − r — базис в ядре оператора. Фундаментальной системой решений однородной системы (1) называется базис ядра оператора ^A (точнее, координатные столбцы базисных векторов в Ker ^A ). Это определение можно сформулировать несколько иначе: Фундаментальной системой решений однородной системы (1) называется n − r линейно независимых решений этой системы. Будем обозначать координатные столбцы базисных векторов в Ker ^A X1, X2, … , Xn − r . Теорема о структуре общего решения однородной системы уравнений: Любое решение однородной системы линейных уравнений определяется формулой
где X1, X2, … , Xn − r — фундаментальная система решений однородной системы линейных уравнений и C1, C2, … , Cn − r — произвольные постоянные. Свойства общего решения однородной системы уравнений: При любых значениях C1, C2, … , Cn − r X , определяемое формулой (3), является решением системы (1). Каково бы ни было решение X0 , существуют числа C10, … , Cn − r0 такие, что
Вывод: Чтобы найти фундаментальную систему и общее решение однородной системы, нужно найти базис ядра соответствующего линейного оператора. Эквивалентные преобразования системы линейных уравненийСистемы линейных уравнений Линейное уравнение (л.у.) – уравнение вида |
Система линейных уравнений (СЛУ) – система вида
где 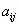
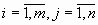
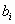
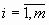
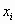
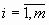
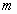
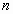
Сокращенная форма записи СЛУ (2)
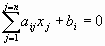
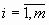
Матричная форма записи СЛУ (2)
где 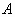
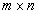
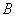
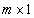
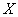
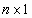
0 – нуль-вектор размерности 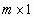
Квадратная СЛУ – СЛУ, состоящая из n уравнений с n переменными.
Решение СЛУ с n переменными – упорядоченная совокупность чисел 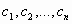
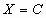
1. Точные методы решения – методы решения, дающие точное решение задачи за конечное число арифметических и логических операций в предположении отсутствия округлений. Применяются для решения задач с малым числом переменных – не более 10 3 .
2. Итеративные методы решения – методы решения, дающие возможность получить решение с заданной точностью или точное решение. Применяются для решения задач со средним числом переменных – не более 10 6 . Требуют меньше вычислений, чем точные методы решения.
3. Вероятностные методы решения. Применяются для решения задач с большим числом переменных – более 10 6 .
Совместная СЛУ – СЛУ, имеющая одно или несколько решений.
Определенная СЛУ – совместная СЛУ, имеющая единственное решение.
Неопределенная СЛУ – совместная СЛУ, имеющая более одного решения.
Несовместная СЛУ – СЛУ, не имеющая ни одного решения.
Однородная СЛУ (ОСЛУ) – СЛУ, все свободные члены которой равны нулю
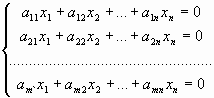
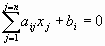
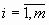
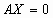
1. Любая ОСЛУ имеет хотя бы одно решение – тривиальное решение, т.е. 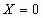
2. Для того чтобы ОСЛУ имела нетривиальные решения, необходимо и достаточно, чтобы ранг матрицы коэффициентов системы был меньше количества переменных системы.
Неоднородная СЛУ (НСЛУ) – СЛУ, у которой хотя бы один свободный член отличен от нуля
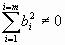
1. Для того чтобы НСЛУ была совместной СЛУ, необходимо и достаточно, чтобы ранг матрицы коэффициентов равен рангу расширенной матрицы (7).
2. Квадратная НСЛУ с вырожденной матрицей коэффициентов может быть совместной неопределенной системой или несовместной системой.
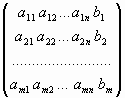
где 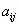
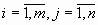
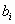
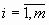
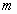
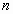
Равносильные СЛУ – две СЛУ, множества решений которых совпадают.
1. Всякие две несовместные системы считаются равносильными.
Элементарные преобразования СЛУ :
— умножение некоторого уравнения системы на отличное от нуля число;
— прибавление к одному уравнению системы другого ее уравнения, умноженного на произвольное число;
— перестановка местами двух уравнений системы;
— перестановка местами двух неизвестных вместе с коэффициентами у всех уравнений.
Эквивалентные СЛУ – две СЛУ, полученные одна из другой с помощью элементарных преобразований.
1. Любые две эквивалентные СЛУ – равносильные.
2. Любая СЛУ приводится посредством элементарных преобразований к системе с трапециевидной матрицей.
3. Любая квадратная СЛУ с невырожденной матрицей коэффициентов A приводится посредством элементарных преобразований к системе с треугольной матрицей.
http://lektsii.org/7-2182.html
http://algmet.simulacrum.me/theory_a4m/slau/index.htm



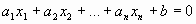
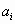 – числа, называемые коэффициентами л.у.,
– числа, называемые коэффициентами л.у., 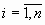 ,
,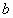 – число, называемое свободным членом л.у.
– число, называемое свободным членом л.у.