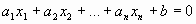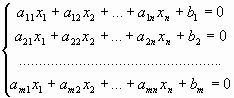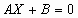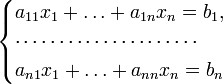Эквивалентные системы линейных уравнений элементарные преобразования слу

Эквивалентные системы линейных уравнений элементарные преобразования слу

Системы линейных уравнений

Линейное уравнение (л.у.) – уравнение вида

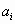
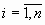
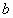
где – числа, называемые коэффициентами л.у., ,

– число, называемое свободным членом л.у.

Система линейных уравнений (СЛУ) – система вида

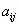
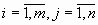
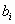
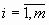
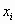
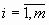
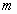
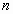
где – числа, называемые коэффициентами СЛУ, ,

– числа, называемые свободными членами СЛУ, ,

– переменные СЛУ, ,

– количество уравнений СЛУ,

– количество переменных СЛУ.

Сокращенная форма записи СЛУ (2)

, .

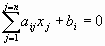
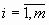
Матричная форма записи СЛУ (2)

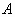
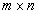
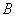
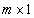
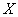
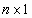
где – матрица коэффициентов СЛУ размерности ,

– вектор свободных членов СЛУ размерности ,

– вектор переменных СЛУ размерности ,

0 – нуль-вектор размерности .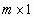

Квадратная СЛУ – СЛУ, состоящая из n уравнений с n переменными.

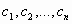
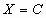
Решение СЛУ с n переменными – упорядоченная совокупность чисел ( для(4)), являющихся решением каждого из уравнений, входящих в систему.

1. Точные методы решения – методы решения, дающие точное решение задачи за конечное число арифметических и логических операций в предположении отсутствия округлений. Применяются для решения задач с малым числом переменных – не более 10 3 .

2. Итеративные методы решения – методы решения, дающие возможность получить решение с заданной точностью или точное решение. Применяются для решения задач со средним числом переменных – не более 10 6 . Требуют меньше вычислений, чем точные методы решения.

3. Вероятностные методы решения. Применяются для решения задач с большим числом переменных – более 10 6 .

Совместная СЛУ – СЛУ, имеющая одно или несколько решений.

Определенная СЛУ – совместная СЛУ, имеющая единственное решение.

Неопределенная СЛУ – совместная СЛУ, имеющая более одного решения.

Несовместная СЛУ – СЛУ, не имеющая ни одного решения.

Однородная СЛУ (ОСЛУ) – СЛУ, все свободные члены которой равны нулю

,

, ,

.

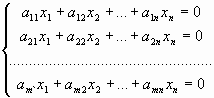
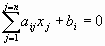
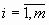
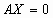
1. Любая ОСЛУ имеет хотя бы одно решение – тривиальное решение, т.е. .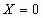

2. Для того чтобы ОСЛУ имела нетривиальные решения, необходимо и достаточно, чтобы ранг матрицы коэффициентов системы был меньше количества переменных системы.

Неоднородная СЛУ (НСЛУ) – СЛУ, у которой хотя бы один свободный член отличен от нуля

.

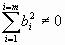
1. Для того чтобы НСЛУ была совместной СЛУ, необходимо и достаточно, чтобы ранг матрицы коэффициентов равен рангу расширенной матрицы (7).

2. Квадратная НСЛУ с вырожденной матрицей коэффициентов может быть совместной неопределенной системой или несовместной системой.

,

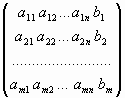
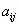
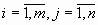
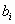
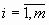
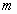
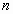
где – коэффициенты СЛУ, ,

– свободные члены СЛУ, ,

– количество уравнений СЛУ,

– количество переменных СЛУ.

Равносильные СЛУ – две СЛУ, множества решений которых совпадают.

1. Всякие две несовместные системы считаются равносильными.

Элементарные преобразования СЛУ :

— умножение некоторого уравнения системы на отличное от нуля число;

— прибавление к одному уравнению системы другого ее уравнения, умноженного на произвольное число;

— перестановка местами двух уравнений системы;

— перестановка местами двух неизвестных вместе с коэффициентами у всех уравнений.

Эквивалентные СЛУ – две СЛУ, полученные одна из другой с помощью элементарных преобразований.

1. Любые две эквивалентные СЛУ – равносильные.

2. Любая СЛУ приводится посредством элементарных преобразований к системе с трапециевидной матрицей.

3. Любая квадратная СЛУ с невырожденной матрицей коэффициентов A приводится посредством элементарных преобразований к системе с треугольной матрицей.

Эквивалентность СЛАУ при элементарных преобразованиях

Определения

Система m линейных уравнений с n неизвестными(или, линейная система) в линейной алгебре — это система уравнений вида

Система (1) называется однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = bm = 0), иначе — неоднородной.

Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

Решение системы (1) — совокупность n чисел c₁, c₂, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все ее уравнения в тождества.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения.

Совместная система вида (1) может иметь одно или более решений.

Решения c₁ (1) , c₂ (1) , …, cn (1) и c₁ (2) , c₂ (2) , …, cn (2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:

Совместная система вида (1) называется определенной, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределенной. Если уравнений больше, чем неизвестных, она называется переопределённой.

Матричная форма Править

Система линейных уравнений может быть представлена в матричной форме как:

или, согласно правилу перемножения матриц,

Методы решения системы (1) Править

Прямые методы Править

§ Метод прогонки — Для трехдиагональных матриц

Приближенные методы Править

§ Метод Якоби (метод итераций)

Метод Крамера (Крамера правило) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причем для таких уравнений решение существует и единственно).

Описание метода

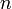
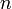
Для системы линейных уравнений с неизвестными (над произвольным полем) (число уравнений совпадает с числом переменных).

с определителем матрицы системы , отличным от нуля, решение записывается в виде:

,

.

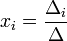
(i-й столбец матрицы системы заменяется столбцом свободных членов).

Рангом матрицы A называется наибольший из порядков миноров матрицы A , отличных от нуля. Ранг нулевой матрицы считается равным нулю.

Алгоритм вычисления ранга матрицы:

• матрица приводится к ступенчатому с помощью элементарных преобразований;
• количество ненулевых строк в полученной матрице будет равно рангу первоначальной матрицы.

Свойства ранга матрицы:

• ранг матрицы не превосходит меньшего из ее размеров;
• ранг матрицы равен нулю тогда и только тогда, когда матрица нулевая;
• ранг матрицы не изменится, если из нее вычеркнуть все нулевые строки и столбцы;
• ранг матрицы не изменится при ее транспонировании;
• элементарные преобразования матрицы не меняют ее ранга

Элементарные преобразования матрицы.

Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.

Определение

Элементарными преобразованиями строк называют:

§ перестановка местами любых двух строк матрицы;

§ умножение любой строки матрицы на константу , ;

§ прибавление к любой строке матрицы другой строки, умноженной на константу , .

Аналогично определяются элементарные преобразования столбцов.

Элементарные преобразования обратимы.

Обозначение указывает на то, что матрица может быть получена из путём элементарных преобразований (или наоборот).

Свойства

Инвариантность ранга при элементарных преобразованиях

Теорема (об инвариантности ранга при элементарных преобразованиях). Если , то .

Эквивалентность СЛАУ при элементарных преобразованиях

Назовём элементарными преобразованиями над системой линейных алгебраических уравнений:

§ умножение уравнения на ненулевую константу;

§ сложение одного уравнения с другим, умноженным на некоторую константу.

Т.е. элементарные преобразования над её расширенной матрицей. Тогда справедливо следующее утверждение:

Напомним, что две системы называются эквивалентными, если множества их решений совпадают.

02. Элементарные преобразования системы линейных уравнений

Определение 5. Элементарными преобразованиями системы линейных уравнений называются ее следующие преобразования:

1) перестановка любых двух уравнений местами;

2) умножение обеих частей одного уравнения на любое число ;

3) прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число k ;

(при этом все остальные уравнения остаются неизменными).

Нулевым уравнением называем уравнение следующего вида:

.

Теорема 1. Любая конечная последовательность элементарных преобразований и преобразование вычеркивание нулевого уравнения переводит одну систему линейных уравнений в равносильную ей другую систему линейных уравнений.

Доказательство. В силу свойства 4 предыдущего пункта достаточно доказать теорему для каждого преобразования отдельно.

1. При перестановке уравнений в системе местами сами уравнения неизменяются, поэтому по определению полученная система равносильная первоначальной.

2. В силу первой части доказательства достаточно доказать утверждение для первого уравнения. Умножим первое уравнение системы (1) на число , получим систему

(2)

Пусть решение системы (1) . Тогда числа удовлетворяют всем уравнениям системы (1). Так как все уравнения системы (2) кроме первого совпадают с уравнениями системы (1), то числа удовлетворяют всем эти уравнениям. Так как числа удовлетворяют первому уравнению системы (1), то имеет место верное числовое равенство:

. (3)

Умножая его на число K, получим верное числовое равенство:

, (4)

Т. о. устанавливаем, что  решение системы (2).

Обратно, если решение системы (2), то числа удовлетворяют всем уравнениям системы (2). Так как все уравнения системы (1) кроме первого совпадают с уравнениями системы (2), то числа удовлетворяют всем эти уравнениям. Так как числа удовлетворяют первому уравнению системы (2), то справедливо числовое равенство (4). Разделив обе его части на число ,получим числовое равенство (3) и доказываем, что  решение системы (1).

Отсюда по определению 4 система (1) равносильна системе (2).

3. В силу первой части доказательства достаточно доказать утверждение для первого и второго уравнения системы. Прибавим к обеим частям первому уравнению системы соответствующие части второго умноженные на число K , получим систему

(5)

Пусть решение системы (1) . Тогда числа удовлетворяют всем уравнениям системы (1). Так как все уравнения системы (5) кроме первого совпадают с уравнениями системы (1), то числа удовлетворяют всем эти уравнениям. Так как числа удовлетворяют первому уравнению системы (1), то имеют место верные числовые равенства:

, (6)

. (7)

Прибавляя почленно к первому равенству второе, умноженное на число K получим верное числовое равенство:

. (8)

Обратно, если решение системы (5), то числа удовлетворяют всем уравнениям системы (5). Так как все уравнения системы (1) кроме первого совпадают с уравнениями системы (5), то числа удовлетворяют всем эти уравнениям. Так как числа удовлетворяют первому уравнению системы (5), то справедливо числовое равенство (8). Вычитая из обеих его частей соответствующие части равенства (7) умноженные на число K получим числовое равенство (6).

Отсюда по определению 4 система (1) равносильна системе (5).

4. Так как нулевому уравнению удовлетворяет любой упорядоченный набор из n чисел, то при вычеркивании нулевого уравнения в системе получим систему равносильную исходной.