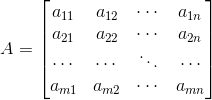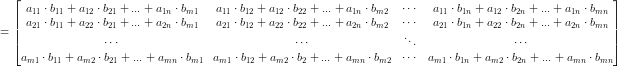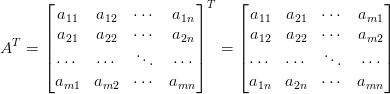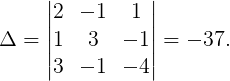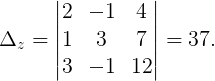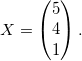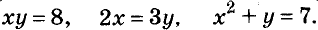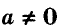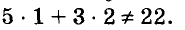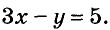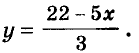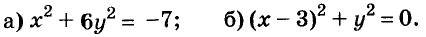Системы линейных алгебраических уравнений
Системой линейных алгебраических уравнений с неизвестными называется система уравнений вида
Числа называются коэффициентами системы ; — свободными членами , — неизвестными . Количество уравнений в системе может быть меньше, больше или равно числу неизвестных.
Решением системы называется упорядоченная совокупность чисел такая, что после замены неизвестных соответственно числами каждое уравнение системы превращается в верное числовое равенство. Система называется совместной , если она имеет хотя бы одно решение. Если система не имеет ни одного решения, то она называется несовместной .
Система (5.1) называется однородной , если все свободные члены равны нулю:
В отличие от однородной, систему общего вида (5.1) называют неоднородной .
Систему (5.1) принято записывать в матричной форме. Для этого из коэффициентов системы составляем матрицу системы
свободные члены записываем в столбец свободных членов
а неизвестные — в столбец неизвестных
Матричная запись неоднородной системы уравнений (5.1) имеет вид
Матричную запись (5.3) системы уравнений можно представить в эквивалентной форме
Тогда решение системы представляется столбцом и удовлетворяет равенству
т.е. столбец свободных членов является линейной комбинацией столбцов матрицы системы.
Относительно системы уравнений нас интересуют ответы на следующие вопросы:
1. Совместна система или нет?
2. Если система совместна, то имеет ли она единственное решение или нет?
3. Если решение единственное, то как его найти?
4. Если система имеет бесконечно много решений, то какова структура множества решений?
5. Как в бесконечном множестве решений системы определить одно решение, наилучшее с практической точки зрения?
6. Если система несовместна, то как определить ее приближенное решение?
Правило Крамера
Рассмотрим случай, когда число уравнений равно числу неизвестных , т.е. систему
где матрица системы — квадратная n-го порядка:
Ее определитель обозначим
Теорема 5.1 (правило Крамера). Если определитель матрицы системы линейных уравнений с неизвестными отличен от нуля, то система имеет единственное решение, которое находится по формулам
где — определитель матрицы, полученной из матрицы системы заменой i-го столбца столбцом свободных членов, т.е.
В самом деле, рассмотрим систему (5.6) как матричное уравнение . Так как определитель матрицы отличен от нуля, по теореме 4.2 заключаем, что матричное уравнение имеет единственное решение:
где — обратная матрица. Запишем i-й элемент столбца , учитывая, что в i-й строке присоединенной матрицы стоят алгебраические дополнения i-го столбца матрицы
Заметим, что в скобках записано разложение определителя по i-му столбцу, т.е. , что и требовалось доказать.
1. На практике при больших правило Крамера не применяется, так как вычисление определителя n-го порядка требует большого числа арифметических операций. Поэтому применяются более экономичные алгоритмы. Обычно, правило Крамера используется, когда нужно найти только несколько неизвестных (например, одну) среди многих. В теоретических исследованиях правило Крамера незаменимо и используется весьма продуктивно.
2. Если и хотя бы один определитель , то система несовместна. Если , то возможны два случая: либо система несовместна, либо имеет бесконечно много решений.
Пример 5.1. Решить систему линейных уравнений с помощью правила Крамера
Решение. Составим матрицу системы . Вычислим ее определитель
Так как определитель отличен от нуля, система имеет единственное решение (см. теорему 5.1). Находим определители и неизвестные
Условие совместности системы линейных уравнений
Рассмотрим систему (5.3) линейных уравнений с неизвестными. Составим блочную матрицу, приписав к матрице справа столбец свободных членов. Получим расширенную матрицу системы :
Эта матрица содержит всю информацию о системе уравнений, за исключением обозначений неизвестных.
Теорема 5.2 Кронекера-Капелли. Система совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы: .
Необходимость следует из равенства (5.5) и следствия 1 теоремы 3.3. Если система имеет решение, то столбец свободных членов есть линейная комбинация столбцов матрицы системы. Поэтому при вычеркивании столбца Ь из расширенной матрицы ее ранг не изменяется. Следовательно, .
Для доказательства достаточности нужно использовать теорему о базисном миноре. Из равенства следует, что базисный минор матрицы является базисным минором расширенной матрицы . Поэтому столбец является линейной комбинацией столбцов базисного минора матрицы , а, значит, и всех столбцов матрицы . Следовательно, существуют числа , удовлетворяющие условию (5.5), т.е. система совместна.
Замечание 5.2. Теорема Кронекера-Капелли дает лишь критерий существования решения системы, но не указывает способа отыскания этого решения.
Пример 5.2. Определить, имеет ли система уравнений решения
Решение. Составим матрицу системы и расширенную матрицу системы
Ранг матрицы равен 2, так как она имеет не равные нулю миноры второго порядка и третья строка этой матрицы равна сумме первых двух строк. Следовательно, третью строку можно вычеркнуть, при этом ранг матрицы не изменится. Ранг расширенной матрицы равен трем, так как она имеет не равный нулю минор третьего порядка, например, минор, составленный из первого, второго и последнего столбцов расширенной матрицы
Следовательно, . Поэтому система несовместна (не имеет решений).
Решение задач по линейной алгебре
| Срок выполнения | от 1 дня |
| Цена | от 50 руб./задача |
| Предоплата | 50 % |
| Кто будет выполнять? | преподаватель или аспирант |
Линейная алгебра: определение, объекты, инструменты
Линейная алгебра – это раздел алгебры, в котором изучаются объекты линейной природы, в частности:
- линейные отображения;
- векторные пространства;
- системы линейных уравнений.
Истоки элементов линейной алгебры относятся к временам Евклида. Различные методы линейной алгебры применялись также у древних вавилонян и древних китайцев.
Основными инструментами, которые применяются в линейной алгебре, являются матрицы, определители матриц, а также сопряжение.
Изучение перечисленных выше объектов образует соответствующие разделы линейной алгебры. Не секрет, что наиболее простым будет раздел, в котором изучаются системы линейных уравнений, методы их решения. Линейные отображения и векторные пространства более сложны для изучения и понимания и, как правило, изучаются на физико-математических факультетах.
Изучение систем линейных уравнений и методов их решения включает рассмотрение следующих понятий:
- матрицы;
- определители;
- операции над матрицами;
- системы линейных алгебраических уравнений (СЛАУ), их виды;
- методы решения СЛАУ.
В данной статье остановим свое внимание именно на выделенном разделе линейной алгебры. Однако не будем сильно вдаваться в теорию, поскольку данная статья не является учебником по линейной алгебре; рассмотрим кратко и только основное, чтобы иметь первоначальное представление о том, с чем приходится иметь дело.
Линейная алгебра: основные понятия и формулы
Матрица – это система элементов (функций, чисел и др. величин), которые расположены в виде прямоугольной таблицы. Общий вид записи матрицы представлен ниже:
Произвольный элемент матрицы обозначается через aij (элемент i-й строки и j-го столбца). Тем, кто знаком с основами алгоритмизации и программирования, будет проще, если сравнить матрицу с двумерным массивом данных (в частном случае с одномерным массивом). Матрица имеет размерность, определяемую количеством строк и столбцов.
Основными действиями над матрицами являются:
- сравнение (для матриц одинаковой размерности):
- сложение и вычитание (для матриц одинаковой размерности):
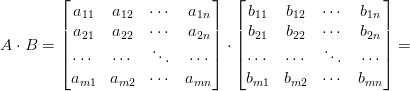
- умножение (количество столбцов первой матрицы равно количеству строк второй матрицы):
- транспонирование:
- обращение:
При нахождении обратной матрицы появляются определитель и алгебраические дополнения, подробнее о которых можно прочитать в любом учебнике по линейной алгебре.
Итак, зная перечисленные формулы, можно смело приступать к их применению, например, при решении СЛАУ вида:
где 
При решении систем линейных уравнений, как правило, используют следующие методы:
- метод Крамера (или формулы Крамера);
- метод Гаусса (реже метод Жордана-Гаусса);
- метод обратной матрицы.
Метод Крамера основан на вычислении определителей матриц, название метода обратной матрицы говорит само за себя. Оба метода применяются в основном при решении систем двух (трех) уравнений с двумя (тремя) неизвестными, что связано с проблематичностью и громоздкостью вычислений определителей и обратных матриц размерности больше трех.
В отличие от предыдущих методов метод Гаусса достаточно легко применяется и для систем с большим числом неизвестных.
В данной статье не будем рассматривать теорию перечисленных методов, а представление о них дадим на соответствующих примерах.
Линейная алгебра: примеры решения задач
Рассмотрим несколько простейших задач из курса линейной алгебры.
Пример 1. Вычислить определитель а) по формуле Саррюса и б) путем разложения по элементам строки: 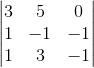
Решение:
а)
б) 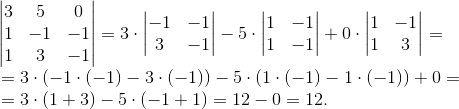
Ответ: Δ = 12 .
Пример 2. Даны две матрицы 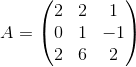
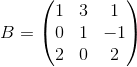
Решение: 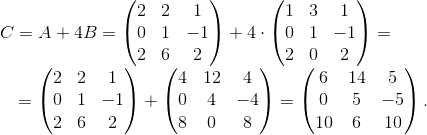
Ответ: 
Пример 3. Решить СЛАУ, используя формулы Крамера: 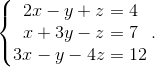
Решение:
Формулы Крамера:
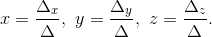
Вычислим все необходимые определители:
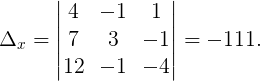
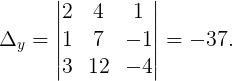
Следовательно, 
Ответ: x = 3 , y = 1 , z = -1 .
Пример 4. Решить СЛАУ методом обратной матрицы: 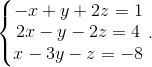
Решение:
Запишем систему уравнений в матричном виде:
AX = B , где
Решение уравнения найдем по формулам:
Найдем обратную матрицу:

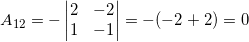




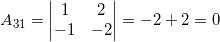



Ответ:
Заключение
Здесь будет правильным привести примерный список учебников для изучения курса линейной алгебры:
- Ильин В.А., Позняк Э.Г. Линейная алгебра: Учеб. Для вузов – 4-е изд. – М. Наука, 1999. – 296 с.
- Мальцев А. И., Основы линейной алгебры, 3-е изд. – М.: Наука, 1970.
Решение линейной алгебры на заказ
Заказать решение задач по линейной алгебре можно здесь. Достаточно просто заполнить форму заказа.
Системы линейных уравнений с примерами решений
Содержание:
Системы уравнений, как и отдельные уравнения, используют для решения сложных и необходимых задач. Системы уравнений бывают с двумя, тремя и более переменными. В этой главе вы ознакомитесь с простейшими системами двух уравнений с двумя переменными. Основные темы лекции:
- уравнения с двумя переменными;
- график линейного уравнения;
- системы уравнений;
- способ подстановки;
- способ сложения;
- решение задач составлением системы уравнений.
Уравнения с двумя переменными
До сих пор мы рассматривали уравнение с одной переменной. Однако существуют задачи, решение которых приводит к уравнениям с двумя переменными.
Пример:
На 22 руб. купили несколько книжек по 5 руб. и географических карт — по 3 руб. Сколько купили книжек и карт?
Решение:
Пусть купили х книжки у карт. За книжки заплатили 5х руб., а за карты — 3у руб. Всего заплатили 22 руб., то есть, 5х + Зу = 22.
Это уравнение с двумя переменными. Приведём и другие примеры таких уравнений с двумя переменными:
Уравнение вида ах + by = с, где а, b, с — данные числа, называется линейным уравнением с двумя переменными х и у. Если
Примеры линейных уравнений:
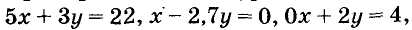
Паре чисел х = -1 и у = 9 удовлетворяет уравнение 5х + Зу -= 22, так как 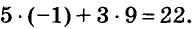
Каждая пара чисел, удовлетворяющая уравнение с двумя переменными, т. е. обращающая это уравнение в верное равенство, называется решением этого уравнения.
Обратите внимание: одно решение состоит из двух чисел, на первом месте записывают значение х, на втором — у. Корнями их не называют.
Чтобы найти решение уравнения с двумя переменными, следует подставить в уравнение произвольное значение первой неременной и, решив полученное уравнение, найти соответствующее значение второй переменной.
Для примера найдем несколько решений уравнения
Если х = 1, то 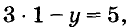
Уравнение 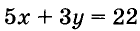
Два уравнения с двумя переменными называют равносильными, если каждое из них имеет те же решения, что и другое. Уравнения, не имеющие решений, также считаются равносильными.
Для уравнения с двумя переменными остаются справедливыми свойства, сформулированные для уравнений с одной переменной.
Обе части уравнения с двумя переменными можно умножить или разделить на одно и то же число, отличное от нуля. Любой член такого уравнения можно перенести из одной части уравнения в другую, изменив его знак на противоположный. В результате получается уравнение, равносильное данному.
Например, уравнение 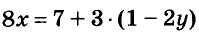
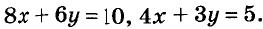
Иногда возникает потребность решить уравнение с двумя переменными во множестве целых чисел, то есть определить решения, являющиеся парами целых чисел. Способы решения таких уравнений определил древнегреческий математик Диофант (III в.), поэтому их называют диофантовыми уравнениями. Например, задача о книжках и картах сводится к уравнению 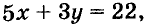
Переменную у из этого уравнения выразим через х:
Будем подставлять в равенство вместо х первые натуральные числа до тех пор, пока не получим целое значение переменной у. Это можно делать устно. Если х = 2, то у = 4. Других натуральных решений уравнение не имеет. Поэтому задача имеет единственное решение: 2 книги и 4 карты.
Пример:
Решение:
а) При любых значениях х и у значения выражения 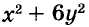
б) Значение выражения 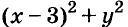
Пример:
Составьте уравнение с двумя переменными, решением которого будет пара чисел (1; -5).
Решение:
Пишем любой двучлен с переменными х и у, например 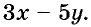
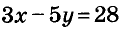
Есть много других линейных уравнений с двумя переменными, имеющих такое же решение (1; -5).
График линейного уравнения с двумя переменными
Рассмотрим уравнение 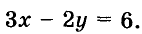
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://reshatel.org/reshenie-zadach/reshenie-zadach-po-linejnoj-algebre/
http://www.evkova.org/sistemyi-linejnyih-uravnenij