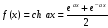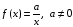Элементы теории функционально дифференциальных уравнений

Определения и понятия теории дифференциальных уравнений

С этой темы мы рекомендуем начинать изучение теории дифференциальных уравнений. В одном разделе мы собрали все основные термины и определения, которые будут применяться при рассмотрении теоретической части. Для того, чтобы облегчить усвоение материала, мы приводим многочисленные примеры.

Дифференциальное уравнение

Дифференциальное уравнение – это уравнение, которое содержит неизвестную функцию под знаком производной или дифференциала.

Обыкновенное дифференциальное уравнение содержит неизвестную функцию, которая является функцией одной переменной. Если же переменных несколько, то мы имеем дело с уравнением в частных производных.

Имеет значение также порядок дифференциального уравнения, за который принимают максимальный порядок производной неизвестной функции дифференциального уравнения.

Обыкновенные дифференциальные уравнения 1 -го, 2 -го и 5 -го порядков:

1 ) y ‘ + 1 = 0 ; 2 ) d 2 y d x 2 + y = x · sin x ; 3 ) y ( 5 ) + y ( 3 ) = a · y , α ∈ R

Уравнения в частных производных 2 -го порядка:

1 ) ∂ 2 u ∂ t 2 = v 2 · ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 + ∂ 2 u ∂ z 2 , u = u ( x , y , z , t ) , v ∈ R ; 2 ) ∂ 2 u ∂ x 2 — ∂ 2 u ∂ y 2 = 0 , u = u ( x , y )

С порядками ДУ разобрались. Далее мы будем в основном рассматривать обыкновенные дифференциальные уравнения n -ого порядка вида F ( x , y , y ‘ , y ‘ ‘ , . . . , y ( n ) ) = 0 или F x , y , d y d x , d 2 y d x 2 , . . . , d n y d x n = 0 , в которых Ф ( x , y ) = 0 — это заданная неявно функция. В тех случаях, когда это будет возможно, неявную функцию мы будем записывать в ее явном представлении y = f ( x ) .

Интегрирование дифференциального уравнения

Интегрирование дифференциального уравнения – это процесс решения этого уравнения.

Решением дифференциального уравнения является функция Ф ( x , y ) = 0 , которая задана неявно и которая обращает данное уравнение в тождество. В некоторых случаях нам нужно будет неявно заданную функцию у выражать через аргумент х явно.

Искать решение дифференциального уравнения мы всегда будем на интервале Х , который задается заранее.

В каких случаях мы будем учитывать интервал Х ? Обычно в условии задач он не упоминается. В этих случаях мы буде искать решение уравнения F ( x , y , y ‘ , y ‘ ‘ , . . . , y ( n ) ) для всех х , при которых искомая функция у и исходное уравнение будут иметь смысл.

Интеграл дифференциального уравнения – это название решения дифференциального уравнения.

Функции y = ∫ x d x или y = x 2 2 + 1 можно назвать решением дифференциального уравнения y ‘ = x .

У одного дифференциального уравнения может быть множество решений.

Функция y = x 3 3 является решением ДУ y ‘ = x 2 . Если мы подставим полученную функцию в исходное выражение, то получим тождество y ‘ = x 3 3 = 1 3 · 3 x 2 = x 2 .

Вторым решением данного дифференциального уравнения является y = x 3 3 + 1 . Подстановка полученной функции в уравнение также превращает его в тождество.

Общее решение ДУ

Общее решение ДУ – это все множество решений данного дифференциального уравнения.

Также общее решение часто носит название общего интеграла ДУ.

Общее решение дифференциального уравнения y ‘ = x 2 имеет вид y = ∫ x 2 d x или y = x 3 3 + C , где C – произвольная постоянная. Из общего интеграла ДУ y = x 3 3 + C мы можем прийти к двум решениям, которые мы привели в прошлом примере. Для этого нам нужно подставить значения С = 0 и C = 1 .

Частное решение ДУ

Частное решение ДУ – это такое решение, которое удовлетворяет условиям, заданным изначально.

Для ДУ y ‘ = x 2 частным решением, которое будет удовлетворять условию y ( 1 ) = 1 , будет y = x 3 3 + 2 3 . Действительно, y ‘ = x 3 3 + 2 3 ‘ = x 2 и y ( 1 ) = 1 3 3 + 2 3 = 1 .

К числу основных задач из теории дифференциальных уравнений относятся:

• задачи Коши;
• задачи нахождения общего решения ДУ при заданном интервале Х ;
• краевые задачи.

Особенностью задач Коши является наличие начальных условий, которым должно удовлетворять полученное частное решение ДУ. Начальные условия задаются следующим образом:

f ( x 0 ) = f 0 ; f ‘ ( x 0 ) = f 1 ; f ‘ ‘ ( x 0 ) = f 2 ; . . . ; f ( n — 1 ) ( x 0 ) = f n — 1

где f 0 ; f 1 ; f 2 ; . . . ; f n — 1 — это некоторые числа.

Особенностью краевых задач является наличие дополнительных условий в граничных точках x 0 и x 1 , которым должно удовлетворять решение ДУ второго порядка: f ( x 0 ) = f 0 , f ( x 1 ) = f 1 , где f 0 и f 1 — заданные числа. Такие задачи также часто называют граничными задачами.

Линейное обыкновенное ДУ n -ого порядка имеет вид:

f n ( x ) · y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = f ( x )

При этом коэффициенты f 0 ( x ) ; f 1 ( x ) ; f 2 ( x ) ; . . . ; f n ( x ) — это непрерывные функции аргумента х на интервале интегрирования.

Уравнение f n ( x ) · y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = f ( x ) будет называться линейным однородным дифференциальным уравнением в том случае, если f ( x ) ≡ 0 . Если нет, то мы будем иметь дело с линейным неоднородным ДУ.

В линейных однородных ДУ коэффициенты f 0 ( x ) = f 0 ; f 1 ( x ) = f 1 ; f 2 ( x ) = f 2 ; . . . ; f n ( x ) = f n могут быть постоянными функциями (некоторыми числами), то мы будем говорить о ЛОДУ с постоянными коэффициентами или ЛНДУ с постоянными коэффициентами. В ЛОДУ с постоянными коэффициентами f ( x ) ≡ 0 , в ЛНДУ с постоянными коэффициентами f ( x ) ненулевая.

Характеристическое уравнение ЛНДУ n -ой степени с постоянными коэффициентами

Характеристическое уравнение ЛНДУ n -ой степени с постоянными коэффициентами – это уравнение n -ой степени вида f n · k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 .

Остальные определения мы будем разбирать в других темах по мере изучения теории.

Элементарное введение в функциональные уравнения

Теория и примеры решения функциональных уравнений

Просмотр содержимого документа
«Элементарное введение в функциональные уравнения»

1.Функциональные уравнения. Их свойства и методы решения. 5

1.1 Определение и примеры функциональных уравнений. 5

1.2 Методы решения функциональных уравнений. 8

2. Решение функциональных уравнений Коши на множестве Q рациональных чисел. 13

2.1 Решение уравнения вида f(x+y)=f(x)+f(y) на Q. 13

2.2 Решение уравнения вида f(x+y)=f(x)∙f(y) на Q. 15

2.3 Решение уравнения вида f(x∙y)=f(x)+f(y) на Q. 17

2.4 Решение уравнения вида f(x∙y)=f(x)∙f(y) на Q. 19

3. Решение функциональных уравнений Коши на R. 22

3.1 Решение уравнения вида f(x+y)=f(x)+f(y) на оси R. 22

3.2 Решение уравнения вида f(x+y)=f(x)∙f(y) на оси R. 23

4. Решение функциональных уравнений Коши в измеримых функциях. 25

5. Класс уравнений типа Коши. 27

Список использованных источников. 30

Курсовая работа посвящена изучению функциональных уравнений, весьма общему классу уравнений, в которых искомой является некоторая функция.

К функциональным уравнениям по существу относятся дифференциальные уравнения, интегральные уравнения, уравнения в конечных разностях; следует, однако, отметить, что название функциональные уравнения обычно не относят к уравнениям этих типов. Под функциональными уравнениями в узком смысле слова понимают уравнения, в которых искомые функции связаны с известными функциями одного или нескольких переменных при помощи операции образования сложной функции. Функциональные уравнения можно также рассматривать как выражение свойства, характеризующего тот или иной класс функций.

Функциональное уравнение — это уравнение, в котором неизвестными являются функции (одна или несколько). Например,

Некоторые функциональные уравнения знакомы нам еще из школьного курса это f(x) = f(-x), f(-x) = — f(x), f(x+T) = f(x), которые задают такие свойства функций, как чётность, нечётность, периодичность.

Задача решения функциональных уравнений является одной из самых старых в математическом анализе. Они появились почти одновременно с зачатками теории функций. Первый настоящий расцвет этой дисциплины связан с проблемой параллелограмма сил. Ещё в 1769 году Даламбер свёл обоснование закона сложения сил к решению функционального уравнения

(1)

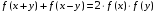
То же уравнение и с той же целью было рассмотрено Пуассоном в 1804 году при некотором предположении аналитичности, между тем как в 1821 году Коши (1789 – 1857) нашёл общие решения

Ряд геометрических задач, приводящих к функциональным уравнениям, рассматривал английский математик Ч. Баббедж (1792—1871). Он изучал, например, периодические кривые второго порядка, определяемые следующим свойством для любой пары точек кривой: если абсцисса второй точки равна ординате первой, то ордината второй точки равна абсциссе первой. Пусть такая кривая является графиком функции у = f(х); (х, f(х)) — произвольная ее точка. Тогда, согласно условию, точка с абсциссой f(х) имеет ординату х. Следовательно,

(2)

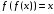
Функциональному уравнению (2) удовлетворяют, в частности, функции: ,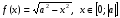

1. Функциональные уравнения. Их свойства и методы решения

1.1 Определение и примеры функциональных уравнений

Функциональные уравнения — весьма общий класс уравнений, в которых искомой является некоторая функция. К функциональным уравнениям, по существу, относятся дифференциальные уравнения, интегральные уравнения, уравнения в конечных разностях. Следует, однако, отметить, что название «функциональные уравнения» обычно не относят к уравнениям этих типов. Под функциональными уравнениями в узком смысле слова понимают уравнения, в которых искомые функции связаны с известными функциями одного или нескольких переменных при помощи операции образования сложной функции. Функциональные уравнения можно также рассматривать как выражение свойства, характеризующего тот или иной класс функций.

Например, функциональное уравнение f (x) = f (-x) характеризует класс чётных функций, функциональное уравнение f(-x) = -f(x) – класс нечетных; функциональное уравнение f (x + 1) = f (x) — класс функций, имеющих период 1, и т.д.

Одним из простейших функциональных уравнений является уравнение

f (x + у) = f (x) + f (y).

Непрерывные решения этого функционального уравнения имеют вид:

Однако в классе разрывных функций это функциональное уравнение имеет и иные решения. С рассмотренным функциональным уравнением связаны

f (x + у) = f (x) f (y),

непрерывные решения которых имеют соответственно вид e Cx , C∙lnx, x a (x 0).

Т.о., эти функциональные уравнения могут служить для определения показательной, логарифмической и степенной функций. В теории аналитических функций функциональные уравнения часто применяются для введения новых классов функций.

Например, двоякопериодические функции характеризуются функциональными уравнениями:

f (z + а) = f (z) и f (z + b) = f (z),

автоморфные функции — функциональными уравнениями:

где a> — некоторая группа дробно-линейных преобразований.

Если функция известна в некоторой области, то знание для неё функционального уравнения позволяет расширить область определения этой функции. Например, функциональное уравнение f (x + 1) = f (x) для периодических функций позволяет определить их значение в любой точке по значениям на отрезке [0, 1]. Этим часто пользуются для аналитического продолжения функций комплексного переменного. Например, пользуясь функциональным уравнением Г (z + 1) = z∙Г (z) и зная значения гамма-функции Г(z) в полосе 0 Re z

Условия симметрии, имеющиеся в какой-либо физической задаче, обусловливают определённые законы преобразования решений этой задачи при тех или иных преобразованиях координат. Этим определяются функциональные уравнения, которым должно удовлетворять решение данной задачи. Значение соответствующих функциональных уравнений во многих случаях облегчает нахождение решений.

Решения функциональных уравнений могут быть как конкретными функциями, так и классами функций, зависящими от произвольных параметров или произвольных функций.

Для некоторых функциональных уравнений общее решение может быть найдено, если известны одно или несколько его частных решений. Например, общее решение функционального уравнения

где j(x) — произвольная функция, а w(x) — частное решение этого функционального уравнения

Для решения функциональных уравнений их во многих случаях сводят к дифференциальным уравнениям. Этот метод даёт лишь решения, принадлежащие классу дифференцируемых функций.

Другим методом решения функциональных уравнений является метод итераций. Этот метод даёт, например, решение уравнения Абеля:

где a(x) — заданная функция и связанного с ним уравнения Шрёдера:

А. Н. Коркин доказал, что если a(х) — аналитическая функция, то уравнение Абеля имеет аналитическое решение. Эти результаты, нашедшие применение в теории групп Ли, привели в дальнейшем к созданию теории итераций аналитических функций. В некоторых случаях уравнение Абеля решается в конечном виде [1].

Элементы теории функционально дифференциальных уравнений

VIII .1. Общие понятия теории обыкновенных дифференциальных уравнений

Обыкновенным дифференциальным уравнением (ДУ) называется некоторая функциональная зависимость, содержащая переменную x , искомую функцию y ( x ) и её производные, то есть

Наивысший порядок производной, входящей в ДУ, называется порядком этого уравнения. Тогда (8.1) – ДУ n — го порядка.

Следовательно, ДУ 1-го порядка имеет вид:

Если из (8.2) выразить , то получим ДУ 1-го порядка, разрешенное относительно производной:

Решением ДУ называется такая функция y ( x ), которая, будучи подставленной вместе со всеми своими производными до n -го порядка в уравнение, обращает его в тождество.

Если неизвестная искомая функция зависит от нескольких переменных, то дифференциальное уравнение называется уравнением в частных производных. Далее будем рассматривать только обыкновенные ДУ.

Методом решения ДУ является интегрирование, а график решения ДУ называется интегральной кривой.

Процесс интегрирования для ДУ n -го порядка повторяется n раз. Следовательно, искомое решение будет содержать ровно n констант интегрирования. Решение ДУ, содержащее константы интегрирования , называется общим решением ДУ:

Если данное решение получено в неявном виде , то оно называется общим интегралом .

Для ДУ 1-го порядка общий интеграл записывае тся в виде g ( x , y , c )=0, а общее решение

Решение ДУ, получаемое из общего решения при конкретных значениях констант интегрирования, называется его частным решением (частным интегралом).

Решение ДУ, не получаемое из общего решения ни при каких значениях констант c_i , называется особым.

С геометрической точки зрения общее решение ДУ 1-го порядка y =φ ( x , c ) есть семейство интегральных кривых на плоскости x 0 y ; особое решение представляет собой огибающую интегрального семейства; частное решение y =φ ( x , c ₀ ) при c = c ₀ – одна кривая из этого семейства, проходящая через точку ( x ₀ ; y ₀ ). Задать эту точку означает задать для данного дифференциального уравнения начальные условия:

Геометрически задание начальных условий подразумевает выделение из всего семейства интегральных кривых выделение именно той кривой, которая проходит через точку с координатами ( x ₀ ; y ₀ ).

Если составить систему, состоящую из самого ДУ и заданных для него начальных условий, то получим задачу Коши для данного ДУ. Запишем задачу Коши для ДУ 1-го порядка:

Теорема 8.1 (о существовании и единственности решения задачи Коши). Если в уравнении функция f ( x , y ) и ее частная производная непрерывны в некоторой области D , содержащей точку ( x 0 ; y 0 ), то существует единственное решение y =φ ( x ) этого уравнения, удовлетворяющее начальному условию (8.6)

Для того чтобы найти частное решение ДУ, удовлетворяющее заданным начальным условиям, необходимо:

1) проинтегрировав ДУ, найти его общее решение (общий интеграл);

2) в общее решение (общий интеграл) подставить заданные начальные условия, получая при этом уравнение (систему уравнений) относительно констант интегрирования c_i , где ;

3) решить уравнение относительно с или систему уравнений относительно c_i ;

4) найденные значения c или c_i подставить в общее решение ДУ 1-го или n -го порядка соответственно.

Пример 8.1. Найти частное решение ДУ , удовлетворяющее начальн ому услови ю y (1)=4.

Решение. Учитывая, что имеем или . Проинтегрировав данное уравнение , получим общее решение y = 2 x 3 + c . Подставим в него начальные условия y (1)=4:

4=2+ c или c =2. Данное значение константы подставим в общее решение: y = 2 x 3 + 2 – искомое частное решение

Рассмотрим, в чем состоит геометрическая интерпретация ДУ 1-го порядка. Уравнения (8.2) и (8.3) устанавливают зависимость между координатами точки ( x , y ) и угловым коэффициентом касательной к интегральной кривой, проходящей через эту точку. Следовательно, ДУ (8.3) задает на координатной плоскости x 0 y поле направлений. Кривая, во всех точках которой направление поля одинаково, называется изоклиной. Для приближенного построения интегральных кривых пользуются изоклинами. Уравнение изоклины можно получить при , то есть f ( x , y )= c .

Ряд прикладных задач приводит к понятию обыкновенного дифференциального уравнения.

Задача 8.1 (о движении частицы в вязкой среде). Определить скорость частицы постоянной массы m, движущейся под действием силы тяжести в вязкой среде ( k >0 – коэффициент вязкости).

Решение . Найдем зависимость, по которой изменяется скорость частицы. Согласно основному закону динамики

, где m – масса частицы, t – время, – сила тяжести; сила сопротивления среды . Это векторное уравнение равносильно системе из трех скалярных уравнений, вид которой зависит от выбора системы координат. Направим ось 0x − вдоль направления движения (вертикально вниз). Тогда − проекции сил на ось 0x, где v – модуль скорости. Следовательно, в системе остается одно уравнение:

. Преобразовав, получим:

−линейное дифференциальное уравнение первого порядка относительно искомой функции скорости v ( t ). Методика решения данного вида уравнений изложена несколько ниже, в пункте VIII .2 (подпункт 4)

Закон «естественного роста» описывается дифференциальным уравнением . Общее свойство двух переменных величин x и t , входящих в уравнение, состоит в том, что скорость изменения одной из них x по отношению к другой t пропорциональна имеющемуся количеству величины x в рассматриваемый момент времени t . Должны быть заданы начальные условия задачи − значение x ₀ в начальный момент времени t = t ₀ . Положительный коэффициент пропорциональности k >0 характеризует непрерывный прирост вещества, отрицательный k x , вступившего в химическую реакцию (например, брожения), от времени t.

Закон размножения бактерий характеризует з ависимость массы m пищевых бактерий от времени t и имеет вид .

Закон охлаждения тел − это з акон изменения температуры тела (например, молока после пастеризации) в течение времени:

, где T ( t ) – температура тела в момент времени t ,

t ₀ – температура воздуха (среды охлаждения), до которой тело остывает.

Заметим, что во всех приведенных задачах, которые привели нас к соответствующим обыкновенным дифференциальным уравнениям, k – это некоторый коэффициент пропорциональности.