Уравнение регрессии

Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии

В сервисе для нахождения параметров регрессии используется МНК. Система нормальных уравнений для линейной регрессии: 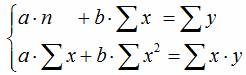. Также можно получить ответ, используя матричный метод. см. также Статистические функции в Excel

Уравнение парной регрессии относится к уравнению регрессии первого порядка. Если эконометрическая модель содержит только одну объясняющую переменную, то она имеет название парной регрессии. Уравнение регрессии второго порядка и уравнение регрессии третьего порядка относятся к нелинейным уравнениям регрессии.

Пример . Осуществите выбор зависимой (объясняемой) и объясняющей переменной для построения парной регрессионной модели. Дайте графическое изображение регрессионной зависимости. Определите теоретическое уравнение парной регрессии. Оцените адекватность построенной модели (интерпретируйте R-квадрат, показатели t-статистики, F-статистики).
Решение будем проводить на основе процесса эконометрического моделирования.
1-й этап (постановочный) – определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли.
Спецификация модели — определение цели исследования и выбор экономических переменных модели.
Ситуационная (практическая) задача. По 10 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих x (в %).
2-й этап (априорный) – предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений, в частности относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих в виде ряда гипотез.
Уже на этом этапе можно говорить о явной зависимости уровня квалификации рабочего и его выработкой, ведь чем опытней работник, тем выше его производительность. Но как эту зависимость оценить?
Парная регрессия представляет собой регрессию между двумя переменными – y и x , т. е. модель вида:

Построение эмпирического уравнения прямой регрессии.

Критерий согласия Пирсона.

Достоинствоуниверсальность: проверяет гипотезы о различных законах распределения.

1. Проверка гипотезы о нормальном распределении.

Пусть получена выборка объема, разделим интервал на s равных частей и будем считать, что значения вариант, попавших в каждый интервал, приближенно равны числу, задающему середину интервала. Подсчитав число вариант, попавших в каждый интервал, составим сгруппированную выборку: х₁ х₂ … х_s; n₁ n₂ … n_s , где х_i – значения середин интервалов, а n_i – число вариант, попавших в i-й интервал (эмпи-рические частоты). По полученным данным вычисляем и σ_В. Проверим что ген. совокупность распределена по норм. закону с параметрами M(X) = , D(X) = . можно найти количество чисел из n, которое должно оказаться в каждом интервале при этом предположении. по табл значений функции Лапласа найдем вер. попадания в i-й интервал: ,где а_i и b_i — границы i-го интервала. Умножив полученные вероятности на n, найдем теоретические частоты: n_i=n·p_i. цель – сравнить эмпир и теоретич частоты, которые, отличаются друг от друга, и выяснить, являются ли эти различия несущественными, не опровергающими гипотезу о нормальном распределении исследуемой случайной величины, или они противоречат этой гипотезе. Для этого используется критерий в виде случайной величины (1) для проверки нулевой гипотезы Н₀: генеральная совокупность распределена нормально – нужно вычислить по выборке наблюдаемое значение критерия: , а по таблице критических точек распределения χ 2 найти критическую точку , используя известные значения α и k=s–3. Если — Н₀ принимают, при ее отвергают.

Проверка гипотезы о равномерном распределении.

При использовании критерия Пирсона для проверки гипотезы о равномерном распределении генеральной совокупности с предполагаемой плотностью вероятности

(2)необходимо, вычислив по имеющейся выборке значение , оценить параметры а и b по формулам:

, где а* и b* — оценки а и b. для равномерного распределения М(Х) = , , откуда можно получить систему для определения а* и b*: , решением которой являются выражения (2). Предполагая, что , можно найти теоретические частоты по формулам Здесь s – число интервалов, на которые разбита выборка.

Наблюдаемое значение крит П. вычисл по форм (1), а критическое – по таблице с учетом числа степеней свободы k=s–3. границы критической области определяются, как и для проверки гипотезы о нормальном распределении.

3. Проверка гипотезы о показательном распределении. разбив выборку на интервалы, рассмотрим последовательность вариант , равноотстоящих друг от друга (считаем, что все варианты, попавшие в i – й интервал, принимают значение, совпадающее с его серединой), и соответствующих им частот n_i (число вариант выборки, попавших в i – й интервал). Вычислим по этим данным и примем в качестве оценки параметра λ величину . Тогда теоретические частоты вычисляются по формуле

сравниваются наблюдаемое и критическое значение крит П с учетом число степеней свободы k=s–2.

Критерий Колмогорова

применяется для проверки простой гипотезы Н₀ независимые одинаково распределенные случайные величины Х₁, Х₂, …, Х_п имеют заданную непрерывную функцию распределения F(x). Найдем функцию эмпирического распределения F_n(x) и будем искать границы двусторонней критической области, определяемой условием (1). Он доказал, что в случае справедливости гипотезы Н₀ распределение статистики D_n не зависит от функции F(x), и при где — (2)- критерий Колмогорова, значения можно найти в соответствующих таблицах. Критическое значение критерия λ_п(α) вычисляется по заданному уровню значимости α как корень уравнения . Можно показать, что приближенное значение вычисляется по формуле , где z – корень уравнения . На практике для вычисления значения статистики D_n используется то, что , где а — вариационный ряд, построенный по выборке Х₁, Х₂, …, Х_п. Можно дать следующее геометрическое истолкование критерия Колмогорова: если изобразить на плоскости Оху графики функций F_n(x), F_n(x) ±λ_n(α) (рис. 1), то гипотеза Н₀ верна, если график функции F(x) не выходит за пределы области, лежащей между графиками функций F_n(x) -λ_n(α) и F_n(x) +λ_n(α). х Приближенный метод проверки нормальности распределения, связанный с оценками коэффициентов асимметрии и эксцесса. Определим по аналогии с соответствующими понятиями для теоретического распределения асимметрию и эксцесс эмпирического распределения. Определение асимметрия эмпирического распределения определяется , (3) где m₃ – центральный эмпирический момент третьего порядка. Эксцесс эмпирического распределения определяется , (4) где m₄ – центральный эмпирический момент четвертого порядка. Для нормально распределенной случайной величины асимметрия и эксцесс=0. Поэтому, если соответствующие эмпирические величины достаточно малы, можно предположить, что ген совокупность распределена по нормальному закону.

45. Основные понятия корреляционного и регрессионного анализа. Для выявления наличия связи, ее характера и направления используются методы приведения параллельных данных, аналитических группировок, графический, корреляции и регрессии.

Метод проведения параллельных данных основан на сопоставлении двух или нескольких рядов статистических величин. Данное сопоставление позоляет установить наличие связи и получить представление о ее характере.

Графический метод

Графическая взаимосвязь двух признаков изображается с помощью поля корреляции.

Корреляция – это статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.

1) парная корреляция – связь между двумя признаками (между двумя факторными либо между факторным и результативным признаком)

2) частная корреляция – зависимость между результативным и одним факторным признаком при фиксированном значении других факторных признаков

3) множественная корреляция – зависимость результативного и двух и более факторных признаков.

Корреляционный анализ имеет своей задачей количественное определение тесноты связи между двумя признаками.

Теснота связи количественно выражается величиной коэффициентов корреляции.

Теснота связи при линейной зависимости измеряется с помощью линейного коэффициента корреляции:

Теснота связи при криволинейной зависимости измеряется с помощью корреляционного отношения. Различают эмпирическое и теоретическое корреляционное отношение.

Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение одной величины обусловлено влиянием одной или нескольких независимых величин (факторов).

По направлению связи различают:

А) прямую регрессию (положительную), возникающую при условии, если с увеличением или уменьшением независимой величины значения зависимой также соответственно увеличиваются или уменьшаются;

Б) обратную (отрицательную) регрессию, появляющуюся при условии, что с увеличением или уменьшением независимой величины зависимая соответственно уменьшается или увеличивается.

Построение эмпирического уравнения прямой регрессии.

Часто приходится рассматривать такие системы (Х, Y), для которых обе линии регрессии представляют собой прямые. Тогда говорят о линейной корреляции между Х и Y. В этом случае уравнения прямых регрессии имеют следующий вид:

, (1) . (2) Уравнение (1) определяет уравнение прямой регрессии Y на Х, а уравнение (2) – прямой регрессии X на Y. Здесь r = r[X,Y] – коэффициент корреляции между Х и Y. При r = ±1 обе прямые сливаются в одну – ту самую прямую у = ах + b, на которой лежат все точки (Х,Y). Предположим, что между случайными величинами Х и Y имеет место линейная корреляция. Возникает задача о приближенном построении прямых регрессий по данным наблюдений над системой (Х, Y). Подход к решению этой задачи указывают сами формулы (1) и (2). Если входящие в них параметры m_X, m_Y, σ_X, σ_Y, r

заменить их эмпирическими оценками, то получим , и две прямые ; (1*) , (2*)

которые естественно рассматривать как эмпирические прямые регрессии. Для нахождения эмпирических прямых регрессий нужно располагать пятью оценками . Они находятся по данным наблюдений над системой (Х,Y). Если в результате n независимых наблюдений получены точки (х₁, у₁), (х₂, у₂), …, (х_n, y_n), то требуемые оценки вычисляем по формулам:

; , где . Эмпирические прямые регрессии по смыслу служат для «выравнивания» приблизительно линейной вероятностной зависимости. Мы записали уравнения этих прямых, руководствуясь аналогией с уравнениями «теоретических» прямых регрессий (1) и (2). Можно, однако, привести более глубокие соображения, обосновывающие роль эмпирических прямых (1*) и (2*). Эти соображения связаны с так называемым методом наименьших квадратов

РЕГРЕССИОННЫЙ АНАЛИЗ

В практических исследованиях возникает необходимость аппроксимировать (описать приблизительно) диаграмму рассеяния математическим уравнением . То есть зависимость между переменными величинами Y и Х можно выразить аналитически с помощью формул и уравнений и графически в виде геометрического места точек в системе прямоугольных координат. График корреляционной зависимости строится по уравнениям функции и , которые называются регрессией (термин “регрессия” происходит от лат. regressio — движение назад). Здесь и — средние арифметические из числовых значений зависимых переменных Y и X .
Для выражения регрессии служат эмпирические и теоретические ряды, их графики — линии регрессии , а также корреляционные уравнения (уравнения регрессии) и коэффициент линейной регрессии.
Показатели регрессии выражают корреляционную связь двусторонне, учитывая изменение средней величины признака Y при изменении значений x i признака X , и, наоборот, показывают изменение средней величины признака Х по измененным значениям y i признака Y . Исключение составляют временные ряды, или ряды динамики, показывающие изменение признаков во времени. Регрессия таких рядов является односторонней.
Ряды регрессии , особенно их графики, дают наглядное представление о форме и тесноте корреляционной связи между признаками, в чем и заключается их ценность. Форма связи между показателями, влияющими на уровень спортивного результата и общей физической подготовки занимающихся физической культурой и спортом, может быть разнообразной. И поэтому задача состоит в том, чтобы любую форму корреляционной связи выразить уравнением определенной функции (линейной, параболической и т.д.), что позволяет получать нужную информацию о корреляции между переменными величинами Y и X , предвидеть возможные изменения признака Y на основе известных изменений X , связанного с Y корреляционно.

Линии регрессии, как показано, пересекаются в точке 0 ( ), соответствующей средним арифметическим значениям корреляционно связанных друг с другом признаков Y и X . Линия АВ, проходящая через эту точку, изображает полную (функциональную) зависимость между переменными вели-чинами Y и X , когда коэффициент корреляции r = 1 . Чем сильнее связь между Y и X , тем ближе линии регрессии к АВ, и, наоборот, чем слабее связь между варьирующими признаками, тем более удаленными оказываются линии регрессии от АВ. При отсутствии связи между признаками, когда r = 0 , линии регрессии оказываются под прямым углом (90°) по отношению друг к другу.
Уравнение регрессии тем лучше описывает зависимость, чем меньше рассеяние диаграммы, чем больше теснота взаимосвязи. Уравнение прямой линии пригодно для описания только линейных зависимостей. В случае не-линейных зависимостей математическая запись может отображаться уравнениями параболы, гиперболы и др.
Необходимо также сделать одно важное замечание о значении показателей, характеризующих взаимосвязь признаков (коэффициентов корреляции, регрессии и т. п.). Все они дают лишь количественную меру связи, но ничего не говорят о причинах зависимости. Определить эти причины — дело самого исследователя.

Значение этой оценки, если r = , равно нулю и, если r = 0 , максимально. Остаточное среднее квадратическое отклонение характеризует колеблемость Y относительно линии регрессии по Х в прямом уравнении регрессии и, наоборот, в обратном случае. А, следовательно, чем меньше вели-чина относительной погрешности уравнения регрессии, тем точнее будет оно осуществлять прогноз значений одного показателя по заранее известным значениям другого.

Эта формула ценна тем, что, во-первых, может быть использована для нахождения неизвестной величины коэффициента корреляции по известным значениям коэффициента регрессии b y/x и b x/y , а во-вторых, позволяет контролировать правильность расчета коэффициента корреляции, если известны величины b y/x и b x/y . Знак выборочного коэффициента корреляции совпадает со знаком выборочных коэффициентов регрессии, что следует из формулы (2.3). Если зависимость между признаками функциональная, то b y/x = 1 / b x/y и, следовательно, r = 1 . И, наоборот, при полном отсутствии взаимосвязи между признаками b y/x = 0, b x/y = 0 , и r = 0 .

Эти уравнения удобны для определения параметров при отыскивании эмпирических уравнений регрессии в практической работе для точности прогнозирования результатов.