Эмпирическое уравнение парной линейной регрессии

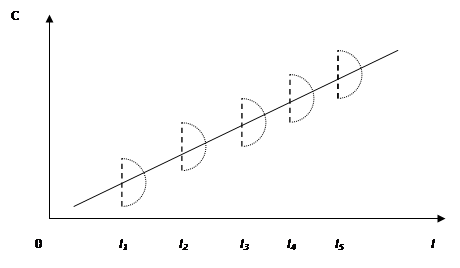
Уравнение регрессии

Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии

В сервисе для нахождения параметров регрессии используется МНК. Система нормальных уравнений для линейной регрессии: 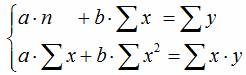. Также можно получить ответ, используя матричный метод. см. также Статистические функции в Excel

Уравнение парной регрессии относится к уравнению регрессии первого порядка. Если эконометрическая модель содержит только одну объясняющую переменную, то она имеет название парной регрессии. Уравнение регрессии второго порядка и уравнение регрессии третьего порядка относятся к нелинейным уравнениям регрессии.

Пример . Осуществите выбор зависимой (объясняемой) и объясняющей переменной для построения парной регрессионной модели. Дайте графическое изображение регрессионной зависимости. Определите теоретическое уравнение парной регрессии. Оцените адекватность построенной модели (интерпретируйте R-квадрат, показатели t-статистики, F-статистики).
Решение будем проводить на основе процесса эконометрического моделирования.
1-й этап (постановочный) – определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли.
Спецификация модели — определение цели исследования и выбор экономических переменных модели.
Ситуационная (практическая) задача. По 10 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих x (в %).
2-й этап (априорный) – предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений, в частности относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих в виде ряда гипотез.
Уже на этом этапе можно говорить о явной зависимости уровня квалификации рабочего и его выработкой, ведь чем опытней работник, тем выше его производительность. Но как эту зависимость оценить?
Парная регрессия представляет собой регрессию между двумя переменными – y и x , т. е. модель вида:

Парная линейная регрессия. Задачи регрессионного анализа

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Понятие линейной регрессии. Парная линейная регрессия

Линейная регрессия — выраженная в виде прямой зависимость среднего значения какой-либо величины от некоторой другой величины. В отличие от функциональной зависимости y = f(x) , когда каждому значению независимой переменной x соответствует одно определённое значение величины y, при линейной регрессии одному и тому же значению x могут соответствовать в зависимости от случая различные значения величины y.

Если в результате наблюдения установлено, что при каждом определённом значении x существует сколько-то (n) значений переменной y, то зависимость средних арифметических значений y от x и является регрессией в статистическом понимании.

Если установленная зависимость может быть записана в виде уравнения прямой

то эта регрессионная зависимость называется линейной регрессией.

О парной линейной регрессии говорят, когда установлена зависимость между двумя переменными величинами (x и y). Парная линейная регрессия называется также однофакторной линейной регрессией, так как один фактор (независимая переменная x) влияет на результирующую переменную (зависимую переменную y).

В уроке о корреляционной зависимости были разобраны примеры того, как цена на квартиры зависит от общей площади квартиры и от площади кухни (две различные независимые переменные) и о том, что результаты наблюдений расположены в некотором приближении к прямой, хотя и не на самой прямой. Если точки корреляционной диаграммы соединить ломанной линией, то будет получена линия эмпирической регрессии. А если эта линия будет выровнена в прямую, то полученная прямая будет прямой теоретической регрессии. На рисунке ниже она красного цвета (для увеличения рисунка щёлкнуть по нему левой кнопкой мыши).

По этой прямой теоретической регрессии может быть сделан прогноз или восстановление неизвестных значений зависимой переменной по заданным значениям независимой переменной.

В случае парной линейной регрессии для данных генеральной совокупности связь между независимой переменной (факториальным признаком) X и зависимой переменной (результативным признаком) Y описывает модель

,

— свободный член прямой парной линейной регрессии,

— коэффициент направления прямой парной линейной регрессии,

— случайная погрешность,

N — число элементов генеральной совокупности.

Уравнение парной линейной регрессии для генеральной совокупности можно построить, если доступны данные обо всех элементах генеральной совокупности. На практике данные всей генеральной совокупности недоступны, но доступны данные об элементах некоторой выборки.

Поэтому параметры генеральной совокупности оценивают при помощи соответствующих параметров соответствующей выборки: свободный член прямой парной линейной регрессии генеральной совокупности заменяют на свободный член прямой парной линейной регрессии выборки , а коэффициент направления прямой парной линейной регрессии генеральной совокупности — на коэффициент направления прямой парной линейной регрессии выборки .

В результате получаем уравнение парной линейной регрессии выборки

— оценка полученной с помощью модели линейной регрессии зависимой переменной Y,

— погрешность,

n — размер выборки.

Чтобы уравнение парной линейной регрессии было более похоже на привычное уравнение прямой, его часто также записывают в виде

.

Уравнение парной линейной регрессии и метод наименьших квадратов

Определение коэффициентов уравнения парной линейной регрессии

Если заранее известно, что зависимость между факториальным признаком x и результативным признаком y должна быть линейной, выражающейся в виде уравнения типа , задача сводится к нахождению по некоторой группе точек наилучшей прямой, называемой прямой парной линейной регрессии. Следует найти такие значения коэффициентов a и b , чтобы сумма квадратов отклонений была наименьшей:

.

Если через и обозначить средние значения признаков X и Y,то полученная с помощью метода наименьших квадратов функция регрессии удовлетворяет следующим условиям:

• прямая парной линейной регрессии проходит через точку ;
• среднее значение отклонений равна нулю: ;
• значения и не связаны: .

Условие метода наименьших квадратов выполняется, если значения коэффициентов равны:

,

.

Пример 1. Найти уравнение парной линейной регрессии зависимости между валовым внутренним продуктом (ВВП) и частным потреблением на основе данных примера урока о корреляционной зависимости (эта ссылка, которая откроется в новом окне, потребуется и при разборе следующих примеров).

Решение. Используем рассчитанные в решении названного выше примера суммы:

Используя эти суммы, вычислим коэффициенты:

Таким образом получили уравнение прямой парной линейной регрессии:

Составить уравнение парной линейной регрессии самостоятельно, а затем посмотреть решение

Пример 2. Найти уравнение парной линейной регрессии для выборки из 6 наблюдений, если уже вычислены следующие промежуточные результаты:

;

;

;

;

Анализ качества модели линейной регрессии

Метод наименьших квадратов имеет по меньшей мере один существенный недостаток: с его помощью можно найти уравнение линейной регрессии и в тех случаях, когда данные наблюдений значительно рассеяны вокруг прямой регрессии, то есть находятся на значительном расстоянии от этой прямой. В таких случаях за точность прогноза значений зависимой переменной ручаться нельзя. Существуют показатели, которые позволяют оценить качество уравнения линейной регрессии прежде чем использовать модели линейной регрессии для практических целей. Разберём важнейшие из этих показателей.

Коэффициент детерминации

Коэффициент детерминации принимает значения от 0 до 1 и в случае качественной модели линейной регрессии стремится к единице. Коэффициент детерминации показывает, какую часть общего рассеяния зависимой переменной объясняет независимая переменная:

,

— сумма квадратов отклонений, объясняемых моделью линейной регрессии, которая характеризует рассеяние точек прямой регрессии относительно арифметического среднего,

— общая сумма квадратов отклонений, которая характеризует рассеяние зависимой переменной Y относительно арифметического среднего,

— сумма квадратов отклонений ошибки (не объясняемых моделью линейной регрессии), которая характеризует рассеяние зависимой переменной Y относительно прямой регресии.

Пример 3. Даны сумма квадратов отклонений, объясняемых моделью линейной регрессии (3500), общая сумма квадратов отклонений (5000) и сумма квадратов отклонений ошибки (1500). Найти коэффициент детерминации двумя способами.

F-статистика (статистика Фишера) для проверки качества модели линейной регрессии

Минимальное возможное значение F-статистики — 0. Чем выше значение статистики Фишера, тем качественнее модель линейной регрессии. Этот показатель представляет собой отношение объясненной суммы квадратов (в расчете на одну независимую переменную) к остаточной сумме квадратов (в расчете на одну степень свободы):

где m — число объясняющих переменных.

Сумма квадратов остатков

Сумма квадратов остатков (RSS) измеряет необъясненную часть дисперсии зависимой переменной:

—

остатки — разности между реальными значениями зависимой переменной и значениями, оценёнными уравнением линейной регрессии.

В случае качественной модели линейной регрессии сумма квадратов остатков стремится к нулю.

Стандартная ошибка регрессии

Стандартная ошибка регрессии (SEE) измеряет величину квадрата ошибки, приходящейся на одну степень свободы модели:

Чем меньше значение SEE, тем качественнее модель.

Пример 4. Рассчитать коэффициент детерминации для данных из примера 1.

Решение. На основании данных таблицы (она была приведена в примере урока о корреляционной зависимости) получаем, что SST = 63 770,593 , SSE = 10 459,587 , SSR = 53 311,007 .

Можем убедиться, что выполняется закономерность SSR = SST — SSE :

Получаем коэффициент детерминации:

.

Таким образом, 83,6% изменений частного потребления можно объяснить моделью линейной регресии.

Интерпретация коэффициентов уравнения парной линейной регрессии и прогноз значений зависимой переменной

Итак, уравнение парной линейной регрессии:

.

В этом уравнении a — свободный член, b — коэффициент при независимой переменной.

Интерпретация свободного члена: a показывает, на сколько единиц график регрессии смещён вверх при x=0, то есть значение переменной y при нулевом значении переменной x.

Интерпретация коэффициента при независимой переменной: b показывает, на сколько единиц изменится значение зависимой переменной y при изменении x на одну единицу.

Пример 5. Зависимость частного потребления граждан от ВВП (истолкуем это просто: от дохода) описывается уравнением парной линейной регрессии . Сделать прогноз потребления при доходе в 20 000 у.е. Выяснить, на сколько увеливается потребление при увеличении дохода на 5000 у.е. Меняется ли потребление, если доход не меняется?

Решение. Подставляем в уравнение парной линейной регрессии x i = 20000 и получаем прогноз потребления при доходе в 20 000 у.е. y i = 17036,4662 .

Подставляем в уравнение парной линейной регрессии x i = 5000 и получаем прогноз увеличения потребления при увеличении дохода на 5000 у.е. y i = 4161,9662 .

Если доход не меняется, то x i = 0 и получаем, что потребление уменьшается на 129,5338 у.е.

Задачи регрессионного анализа

Регрессионный анализ — раздел математической статистики, объединяющий практические методы исследования регрессионной зависимости между величинами по статистическим данным.

Наиболее частые задачи регрессионного анализа:

• установление факта наличия или отсутствия статистических зависимостей между переменными величинами;
• выявление причинных связей между переменными величинами;
• прогноз или восстановление неизвестных значений зависимых переменных по заданным значениям независимых переменных.

Также делаются проверки статистических гипотез о регрессии. Кроме того, при изучении связи между двумя величинами по результатам наблюдений в соответствии с теорией регрессии предполагается, что зависимая переменная имеет некоторое распределение вероятностей при фиксированном значении независимой переменной.

В исследованиях поведения человека, чтобы они претендовали на объективность, важно не только установить зависимость между факторами, но и получить все необходимые статистические показатели для результата проверки соответствующей гипотезы.

Проверка гипотезы о равенстве нулю коэффициента направления прямой парной линейной регрессии

Одна из важнейших гипотез в регрессионном анализе — гипотеза о том, что коэффициент направления прямой регрессии генеральной совокупности равен нулю.

Если это предположение верно, то изменения независимой переменной X не влияют на изменения зависимой переменной Y: переменные X и Y не коррелированы, то есть линейной зависимости Y от X нет.

рассматривают во взаимосвязи с альтернативной гипотезой

.

Статистика коэффициента направления

соответствует распределению Стьюдента с числом степеней свободы v = n — 2 ,

где — стандартная погрешность коэффициента направления прямой линейной регресии b 1 .

Доверительный интервал коэффициента направления прямой линейной регрессии:

.

Критическая область, в которой с вероятностью P = 1 — α отвергают нулевую гипотезу и принимают альтернативную гипотезу:

Пример 6. На основе данных из предыдущих примеров (о ВВП и частном потреблении) определить доверительный интервал коэффициента направления прямой линейной регресии 95% и проверить гипотезу о равенстве нулю коэффициента направления прямой парной линейной регрессии.

Можем рассчитать, что , а стандартная погрешность регрессии .

Таким образом, стандартная погрешность коэффициента направления прямой линейной регресии b 1 :

.

Так как и (находим по таблице в приложениях к учебникам по статистике), то доверительный интервал 95% коэффициента направления прямой парной линейной регрессии:

.

Так как гипотетическое значение коэффициента — нуль — не принадлежит доверительному интервалу, с вероятностью 95% можем отвергнуть основную гипотезу и принять альтернативную гипотезу, то есть считать, что зависимая переменная Y линейно зависит от независимой переменной X.

Парная линейная регрессия

Если функция регрессии линейна, то говорят о линейной регрессии. Модель линейной регрессии (линейное уравнение) является наиболее распространенным (и простым) видом зависимости между экономическими переменными. Кроме того, построенное линейное уравнение может служить начальной точкой эконометрического анализа.

Например, Кейнсом была предложена формула такого типа для моделирования зависимости частного потребления Сот располагаемого дохода I: , где — величина автономного потребления, b — предельная склонность к потреблению. Однако при использовании этой модели при анализе конкретных данных мы практически всегда будем иметь определенную погрешность, так как строгой функциональной зависимости между этими показателями нет. Однако никто не будет отрицать, что люди (домохозяйства) с большим доходом имеют большее в среднем потребление.

Данная ситуация наглядно представлена на рис. 2.

Из предыдущих рассуждений ясно, что линейная регрессия (теоретическое линейное уравнение регрессии) представляет собой линейную функцию между условным математическим ожиданием зависимой переменной Y и одной объясняющей переменной X ( — значения независимой переменной в -м наблюдении, ).

(5)

Отметим, что принципиальной в данном случае является линейность по параметрам и уравнения.

Для отражения того факта, что каждое индивидуальное значение отклоняется от соответствующего условного математического ожидания, необходимо ввести в соотношение (5) случайное слагаемое

(6)

Соотношение (6) называется теоретической линейной регрессионной моделью; и —теоретическими параметрами (теоретическими коэффициентами) регрессии; — случайным отклонением.

Следовательно, индивидуальные значения представляются в виде суммы двух компонент — систематической и случайной ( ), причина появления которой достаточно подробно рассмотрена ранее. В общем виде теоретическую линейную регрессионную модель будем представлять в виде

. (7)

Для определения значений теоретических коэффициентов регрессии необходимо знать и использовать все значения переменных X и Y генеральной совокупности, что практически невозможно.

Таким образом, задачи линейного регрессионного анализа состоят в том, чтобы по имеющимся статистическим данным , , для переменных X и Y:

а) получить наилучшие оценки неизвестных параметров аиb;

б) проверить статистические гипотезы о параметрах модели;

в) проверить, достаточно ли хорошо модель согласуется со статистическими данными (адекватность модели данным наблюдений).

Следовательно, по выборке ограниченного объема мы сможем построить так называемое эмпирическое уравнение регрессии

, (8)

где — оценка условного математического ожидания ; и — оценки неизвестных параметров аи b,называемые эмпирическими коэффициентами регрессии. Следовательно, в конкретном случае

(9)

где отклонение — оценка теоретического случайного отклонения .

В силу несовпадения статистической базы для генеральной совокупности и выборки — оценки и практически всегда отличаются от истинных значений коэффициентов аи b что приводит к несовпадению эмпирической и теоретической линий регрессии. Различные выборки из одной и той же генеральной совокупности обычно приводят к определению отличающихся друг от друга оценок.

Задача состоит в том, чтобы по конкретной выборке , , найти оценки и неизвестных параметров аи bтак, чтобы построенная линия регрессии являлась бы наилучшей в определенном смысле среди всех других прямых. Другими словами, построенная прямая должна быть «ближайшей» к точкам наблюдений по их совокупности. Мерами качества найденных оценок могут служить определенные композиции отклонений , . Например, коэффициенты и эмпирического уравнения регрессии могут быть оценены исходя из условия минимизации следующей суммы:

.

Этот метод нахождения коэффициентов является самым распространенным и теоретически обоснованным. Он получил название метод наименьших квадратов (МНК). Этот метод оценки является наиболее простым с вычислительной точки зрения. Кроме того, оценки коэффициентов регрессии, найденные МНК при определенных предпосылках, обладают рядом оптимальных свойств.

Среди других методов определения оценок коэффициентов регрессии отметим метод моментов (ММ) и метод максимального правдоподобия (ММП).

4. Метод наименьших квадратов

Пусть по выборке , , требуется определить оценки и эмпирического уравнения регрессии (8). В этом случае при использовании МНК минимизируется следующая функция (рис. 3):

. (10)

Нетрудно заметить, что функция Qявляется квадратичной функцией двух параметров и ( ), поскольку , — известные данные наблюдений. Так как функция Qнепрерывна, выпукла и ограничена снизу , то она имеет минимум.

Необходимым условием существования минимума функции двух переменных (10) является равенство нулю ее частных производных по неизвестным параметрам и [1] :

(11)

(12)

Так как , , , для заданной выборки являются по сути числами, то имеем систему 2-х линейных алгебраических уравнений с двумя неизвестными и , решить которую можно любым из известных методов (подстановкой, Гаусса, Крамера, обратной матрицы).

Удобно получить и пользоваться готовыми формулами для вычисления коэффициентов регрессии. Введем средние арифметические

, , , .

Разделив оба уравнения системы (12) на п, получим:

(13)

Таким образом, по МНК оценки параметров и определяются по формулам (13).

Нетрудно заметить, что можно вычислить по формуле:

. (14)

(15)

где r_xy— выборочный коэффициент корреляции; S_x, S_y — стандартные отклонения. Таким образом, коэффициент регрессии пропорционален ковариации и коэффициенту корреляции, а коэффициенты пропорциональности служат для соизмерения перечисленных разномерных величин.

Итак, если коэффициент корреляции r_хууже рассчитан, то легко может быть найден коэффициент парной регрессии по формуле (15).

Если, кроме уравнения регрессии Y на X( ), для тех же эмпирических данных найдено уравнение регрессии Xна Y ( ), то произведение коэффициентов и равно :

. (16)

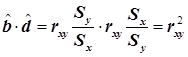
Отметим, что коэффициенты и находятся по формулам, аналогичным формулам (13):

(17)

Характеристики оценок, получаемых по данному методу, следуют из теоремы Гаусса-Маркова.

Теорема Гаусса-Маркова. В предположениях для парной линейной регрессионной модели с пространственной выборкой оценки коэффициентов регрессии а и b, полученные методом наименьших квадратов, имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.

Общий смысл: оценки коэффициентов линейной регрессии аи b, полученные методом наименьших квадратов, являются в определенном смысле «наилучшими» из всех оценок.

Выводы

Проведенные рассуждения и формулы 10 — 17 позволяют сделать ряд выводов:

1. Оценки МНК являются функциями от выборки, что позволяет их легко рассчитывать.

2. Оценки МНК являются точечными оценками теоретических коэффициентов регрессии.

3. Согласно второй формуле соотношения (13), эмпирическая прямая регрессии обязательно проходит через точку .

4. Эмпирическое уравнение регрессии построено таким образом, что сумма отклонений , а также среднее значение отклонения равны нулю.

Действительно, из формулы в соотношении (11) следует, что .

5. Случайные отклонения не коррелированы с наблюдаемыми значениями зависимой переменной Y.

Для обоснования данного утверждения покажем, что ковариация между Y и еравна нулю. Действительно,

.

Покажем, что .Просуммировав по все соотношения (9), получим: , так как .

Разделив последнее соотношение на п, имеем: .

Вычитая из (9) полученное соотношение, приходим к следующей формуле:

. (18)

.

Следовательно, .

6. Случайные отклонения не коррелированы с наблюдаемыми значениями независимой переменной X.

Действительно, в силу второй формулы системы (11) (доказательство выносится для самостоятельной работы). Случайные отклонения , не коррелированы с наблюдаемыми значениями зависимой переменной Y.

Вопросы для самоподготовки

1. Что такое функция регрессии?

2. Чем регрессионная модель отличается от функции регрессии?

3. Назовите основные причины наличия в регрессионной модели случайного отклонения.

4. Назовите основные этапы регрессионного анализа.

5. Что понимается под спецификацией модели, и как она осуществляется?

6. В чем состоит различие между теоретическим и эмпирическим уравнениями регрессии?

7. Дайте определение теоретической линейной регрессионной модели.

8. В чем суть метода наименьших квадратов (МНК)?

9. Приведите формулы расчета коэффициентов эмпирического парного линейного уравнения регрессии по МНК.

10. Как связаны эмпирические коэффициенты линейной регрессии с выборочным коэффициентом корреляции между переменными уравнения регрессии?

11. Какие выводы можно сделать об оценках коэффициентов регрессии и случайного отклонения, полученных по МНК?

12. Проинтерпретируйте коэффициенты эмпирического парного линейного уравнения регрессии.

13. Какое из следующих утверждений истинно, ложно, не определено? Почему?

а) Случайная погрешность 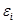и отклонение совпадают.

б) В регрессионной модели объясняющая переменная является фактором изменения зависимой переменной.

в) Линейное уравнение регрессии является линейной функцией относительно входящих в него переменных.

г) Коэффициенты теоретического и эмпирического уравнений регрессии являются по сути СВ.

д) Значения объясняющей переменной парного линейного уравнения регрессии являются СВ.

е) Коэффициент эмпирического парного линейного уравнения регрессии показывает процентное изменение зависимой переменной Y при однопроцентном изменении X.

ж) Коэффициент регрессии Y на X имеет тот же знак, что и коэффициент корреляции .

з) МНК удобен тем, что нахождение оценок коэффициентов регрессии сводится к решению системы линейных алгебраических уравнений.

и) Парная линейная регрессионная модель имеет слабую практическую значимость, так как любая экономическая переменная зависит не от одного, а от большого числа факторов.

14. Можно ли ожидать, с вашей точки зрения, наличия зависимости между следующими показателями:

а) ВНП и объем чистого экспорта;

б) объем инвестиций и процентная ставка;

в) расходы на оборону и расходы на образование;

г) оценки в школе и оценки в университете;

д) объем импорта и доход на душу населения в некоторой стране;

е) цена на кофе и цена на чай?

В случае положительного ответа оцените направление зависимости (прямая или обратная), а также решите, какая из переменных будет в этих случаях объясняющей, а какая — зависимой.

15. Как вы считаете, если по одной и той же выборке рассчитаны регрессии Y на X и X на Y, то совпадут ли в этом случае линии регрессии?

16. Суть МНК состоит в:

а) минимизации суммы квадратов коэффициентов регрессии;

б) минимизации суммы квадратов значений зависимой переменной;

в) минимизации суммы квадратов отклонений точек наблюдений от уравнения регрессии;

г) минимизации суммы квадратов отклонений точек эмпирического уравнения регрессии от точек теоретического уравнения регрессии.

Выберите правильные ответы.

17. Если переменная X принимает среднее по выборке значение , то:

а) наблюдаемая величина зависимой переменной Y равна среднему значению ;

б) рассчитанное по уравнению регрессии значение переменной Y в среднем равно , но не обязательно равно ему в каждом конкретном случае;

в) рассчитанное по уравнению регрессии значение переменной Y равно среднему значению ;

г) отклонение значения минимально среди всех других отклонений.

Какой из выводов вам представляется верным и почему?

[1] В последующих формулах для упрощения знаки сумм будем писать без индексов, предполагая, что суммирование ведется от до . Также для переменных с индексом будем подразумевать, что (если не указано иное).