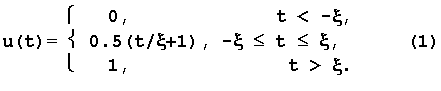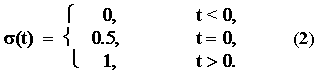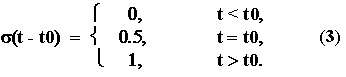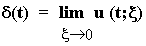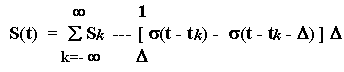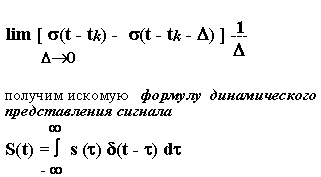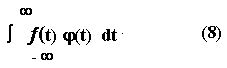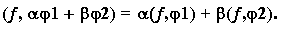Энергетическое представление обобщенного динамического уравнения

2. Математическое описание систем автоматического управления ч. 2.4 — 2.8

Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.

Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

В это части будут рассмотрены:
2.4 Основные виды входных воздействий
2.5. Основные положения и свойства интегральных преобразований Лапласа
2.6. Основные свойства преобразований Лапласа
2.7. Способы нахождения обратных преобразований Лапласа
2.8 Некоторые способы нахождения оригинала по известному изображению

Будет интересно познавательно и жестко.

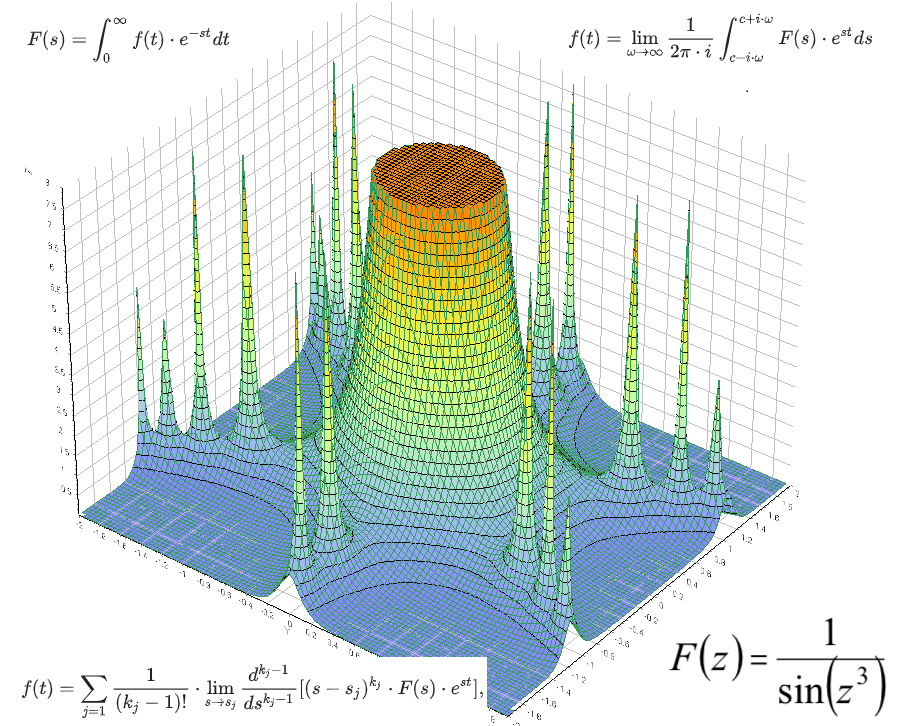
На рисунке 3D график функции косеканс куба, к теме лекции отношения не имеет, но чертовски красив.

2.4 Основные виды входных воздействий

Для того, что бы определить свойства системы нужно осуществить воздействие и посмотреть на реакцию.

В теории управления техническими системами принят ряд стандартных входных воздействий, по реакции на которые определяются динамические свойства (характеристики) системы управления (звена). К таким воздействиям относятся: единичное импульсное воздействие, единичное ступенчатое воздействие, единичное гармоническое воздействие, линейное воздействие и др. Рассмотрим их более подробно…

2.4.1. Единичное ступенчатое воздействие

Данное воздействие является одним из наиболее «жестких» (неблагоприятных) воздействий, по реакции на которое сравниваются переходные свойства (переходной процесс) идентичных или близко идентичных систем.

Реакция системы (звена) на такое воздействие называется переходной функцией.

Единичное ступенчатое воздействие обозначается 1(t) и бывает 3-х видов: два асимметричных и одно симметричное.

Рассмотрим каждый из этих видов воздействий:

0\\ \frac<1><2>, \ если\ t=0\\ 0, \ если\ t 0\\ 0, \ если\ t\leq0 \end \right. $» data-tex=»display»/>

В теории управления наибольшее распространение имеет асимметричное воздействие 1₊ (t), поскольку часто в анализе удобно рассматривать процесс, когда при t0 САР находится в равновесии, и анализ переходных процессов ведется только при t > 0.

Для удобства представления будем в дальнейшем записывать воздействие 1₊(t), опуская индекс. 1₊ (t) ≡ 1(t).

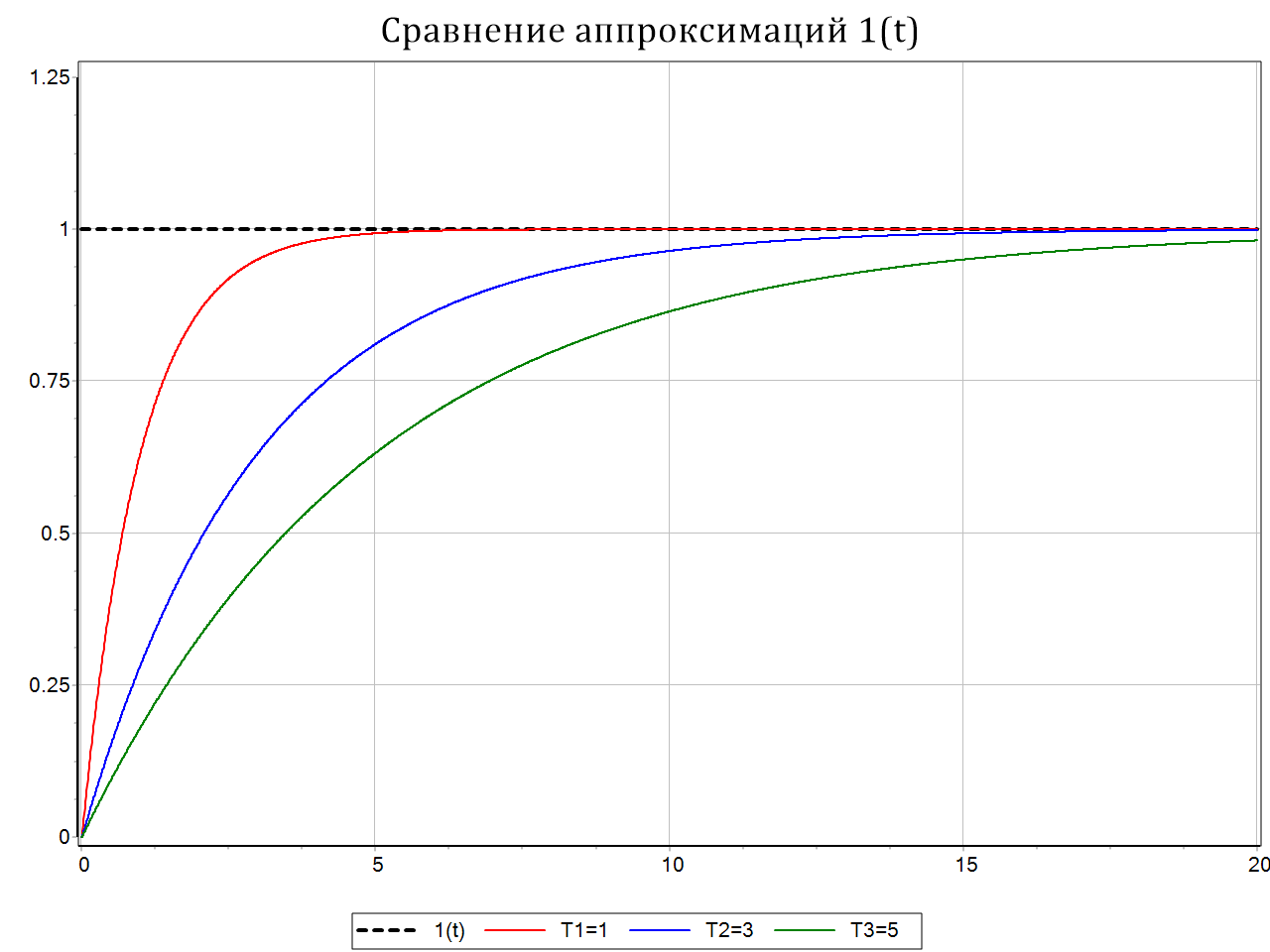
Поскольку рассматриваемое входное воздействие имеет разрыв при t = 0 (что часто нежелательно в численных алгоритмах, использующих конечно-разностную схему), имеется формула, позволяющая приближенно описать единичное ступенчатое воздействие, в виде неразрывной функции:

где Т – постоянная времени, а текущее время

На рисунке 2.4.2 представлена графическая иллюстрация аппроксимации 1(t) по формуле (2.4.2).

2.4.2. Единичное импульсное воздействие: δ — функция Дирака

В математике различают три вида данного воздействия: одно симметричное и два асимметричных

Рассмотрим все эти воздействия:
Симметричное единичное импульсное воздействие δ (t) определено как:

0\\ \infty, если \ t =0\\\ 0, если \ t

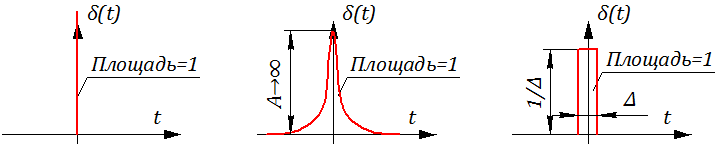
Графическая иллюстрация симметричного единичного импульсного воздействия представлена на рисунке 2.4.3. Фактически δ (t) – импульс (с длительностью стремящейся к нулю и амплитудой, равной бесконечности), площадь которого равна 1.

Для симметричного единичного импульсного воздействия δ(t) существует аналитическая форма представления:

Введем новую переменную , тогда:

Смещенные (асимметричные) единичные импульсные воздействия определяются как:

\epsilon \leq 0\\ \infty, если \ t =\epsilon \\\ 0, если \ t \leq 0\ \end \right. \ \ \ \ \ \int_<-\infty>^ <+\infty>\delta(t) dt = 1;$» data-tex=»display»/>

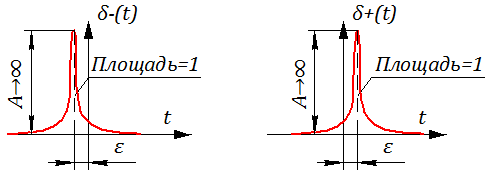
где сколь угодно малое положительное число (ε → 0)

Графическая иллюстрация смещенных единичных импульсных воздействий представлена на рисунке 2.4.4

В дальнейшем в нашем курсе будет использоваться только δ₊ (t). ==> Индекс «+» опускается… ==> δ₊ (t) ≡ δ(t).

Поскольку смещенное единичное импульсное воздействие фактически имеет разрыва при t = 0 (что иногда нежелательно в численных алгоритмах, использующих конечно-разностную схему), имеется формула, позволяющая приближенно описать смещенное единичное импульсное воздействие:

где Т – постоянная времени, а текущее время t>0.
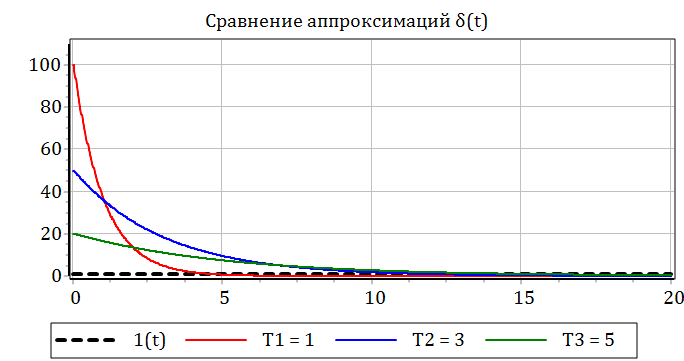
На рисунке 2.4.5 представлена графическая иллюстрация аппроксимации δ(t) по формуле (2.4.3).

Реакция САУ (звена) на воздействие δ (t) называется весовой функцией.

2.4.3. Единичное гармоническое воздействие

Данное воздействие используется для анализа частотных характеристик САУ (звена) в установившемся режиме колебаний в системе, т.е. свойства САУ (звена) исследуются при больших значениях t (времени), когда влияние начальных условий пренебрежимо мало и движение (колебания) системы определяются только входным внешним воздействием.

где ω — круговая частота, [1/с]; , где — частота в Герцах.

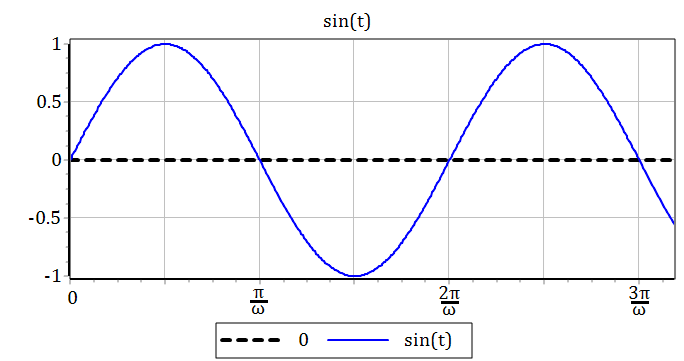
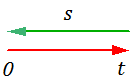
На рисунке 2.4.6 представлен график единичного гармонического воздействия.

Поскольку при анализе частотных характеристик САУ рассматривается режим установившихся вынужденных колебаний САУ (при больших значениях времени t, когда собственная составляющая переходного процесса пренебрежимо мала), то удобнее представить x(t) в показательной форме.

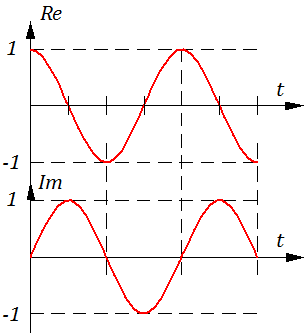
Необходимо отметить, что показательная форма – «комплексное» воздействие, и оно выглядит так (действительная и мнимая части условно показаны на рисунке 2.4.7):

Действительная часть «комплексного» воздействия (Re) – на самом деле косинусоидальное воздействие. Но так как частотные характеристики САУ определяются в режиме установившихся гармонических колебаний (т.е. при «очень-очень» больших значениях t), то не важно, по какому закону вводилось единичное гармоническое воздействие – по «синусу» или по «косинусу».

2.4.4. Линейное воздействие

Данный вид входного воздействия используется для оценки точности систем управления, а именно, для определения скоростных ошибок.

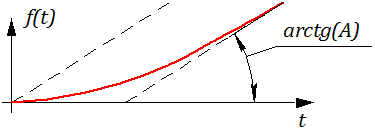
где t ≥ 0, а при t Рисунок 2.4.8 – Линейное входное воздействие

2.5. Основные положения и свойства интегральных преобразований Лапласа

Решение однородного обыкновенного дифференциального уравнения (ОДУ) у_соб(t) записывается в виде (если нет повторяющихся корней):

т.е. все члены уравнения имеют одну и ту же форму. Этот результат наводит на мысль: «а нельзя ли ввести какое-то преобразование, в результате которого уравнение динамики (дифференциальное) можно привести к чисто алгебраическому, решение которого не представляет проблем.» А если затем сделать соответствующее обратное преобразование, то получим у_соб (t), то есть получим цепочку:

Обыкновенное дифференциальное уравнение (ОДУ) Алгебраическое уравнение Решение Обратное преобразование Результат.

Именно такими соображениями руководствовался Лаплас, предлагая такое преобразование, называемое в настоящее время преобразованием Лапласа.

Предположим, что имеется нестационарный процесс f(t). Лаплас предложил ввести интегральное преобразование, которое отображает f(t) на комплексную плоскость согласно соотношению:

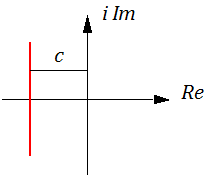
где s = c+i⋅ω: ω ∈ ] -∞; +∞ [; с – абсцисса абсолютной сходимости
(обычно в курсе «УТС» с = 0); f(t) – прообраз (оригинал); F(s) – изображение (образ);

Символическое обозначение преобразования Лапласа:

Преобразование Лапласа существует, если при t Рис. 2.5.2

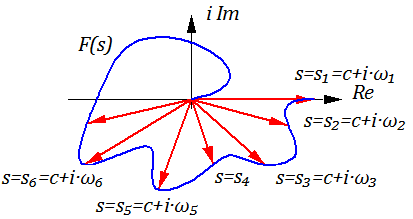
В соответствии с соотношением (2.5.1) переходной процесс f(t) отображается на комплексную плоскость, где каждому значению оператора Лапласа «s» соответствует свой вектор. Линия, соединяющая концы векторов называется годографом.

Обратное преобразование Лапласа определяется следующим соотношением:

Необходимо подчеркнуть, что если условие сходимости выполняется, то любому оригиналу соответствует изображение. Обратное преобразование Лапласа не всегда существует, т.е. если известно F(s), это не означает, что ему соответствует оригинал f(t)!

Прямое преобразование Лапласа символически обозначается:

Обратное преобразование Лапласа обозначается:

Существует двухстороннее преобразование Лапласа , частным случаем которого является обычное преобразование Лапласа

Если при t ≤ 0 функция f(t) = 0, то

Частным случаем двухстороннего преобразования Лапласа (при с = 0, т.е. s = i⋅ω) является преобразование Фурье, определяемое соотношениями:

2.5.1. Использование преобразования Лапласа для операции дифференцирования

Пусть известно и его изображение по Лапласу: выведем выражение для .

Воспользуемся соотношением (2.5.1): , тогда получаем:

где: — начальное условия.
Если начальные условия равны нулю, то ;

Аналогичным способом найдем изображение 2-ой производной:

Если при равны нулю (нулевые начальные условия), то:

Обобщая на производную n-го порядка при нулевых начальных условиях, имеем:

2.5.2. Использование преобразования Лапласа для операции интегрирования

Пусть известно и его изображение по Лапласу: выведем выражение для .

Если начальные условия равные нулю, то:

Таким образом, операция интегрирования в оригинале функции приводит появлению в её изображении “добавке”, равной 1/s.

2.6. Основные свойства преобразований Лапласа

2.6.1. Свойство линейности

Пусть есть процессы описываемые функциями и , каждый из которых имеет свое изображение по Лапласу: . Если то:

Если , то:

2.6.2. Свойство подобия (свойство изменения масштаба)

Пусть — известно, необходимо найти

2.6.3. Свойство запаздывания (теорема запаздывания)

Пусть — известно, необходимо найти

2.6.4. Свойство смещения в комплексной плоскости

2.6.5. Первая предельная теорема

Если — известно, а так же существует , то:

Это означает, что оси «t» и «s» формально направлены в противоположные стороны, т.е. чем больше t, тем меньше s и наоборот.

2.6.6.Вторая предельная теорема

2.7. Способы нахождения обратных преобразований Лапласа по известному изображению

Вычисление оригиналов по известному (данному) изображению можно выполнить:
— по соответствующим таблицам преобразований Лапласа;
— по формулам Хэвисайда;
— разложением на элементарные дроби;
— другими способами.

В математических справочниках приводятся обширные таблицы, по которым можно найти оригиналы большинства изображений. Приведем основыные преобразования:

Таблица основных преобразований Лапласа

Наименование функции	Оригинал	Изображение
1	Единичная импульсная ф-ция	δ(t)	1
2	Единичное ступенчатое воздействие	1(t)
3	Неединичные импульсное и ступенчатое воздействия	a⋅ δ(t); a⋅ 1(t)
4	Экспонента
5	Степенная функция
6	Синусоида
7	Косинусоида
8	Смещенная экспонента
9	Затухающая синусоида
10	Затухающая косинусоида

Однако, нередко бывают и случаи, когда необходимое преобразование отсутствует в таблицах. В этом случае используются различные специальные способы.

Например, если изображение F(s) можно представить в виде отношения полиномов по степеням «s», то наиболее общим и эффективным способом поиска оригинала является формула Хэвисайда.

Если , где и – полиномы по степеням «s», то:

где – полюса изображения, т.е. те значения «s» при которых полином обращается в ноль;
– кратность j – го полюса.

Если уравнение имеет n различных корней, то это означает что полюса F(s) имеют кратность, равную единице, т.е. нет повторяющихся полюсов.

Необходимо отметить, что использование формулы (2.7.1) будет корректно только в том случае, когда степень полинома выше степени полинома . Если степени равны, то необходимо выделить целую часть (разделив «в столбик» полиномы) и чисто дробную часть, после чего для чисто дробной части корректна формула (2.7.1).

2.8 Некоторые способы нахождения оригинала по известному изображению

В качестве иллюстрации возможностей формулы Хэвисайда рассмотрим следующий пример:

Пример 1. Предположим, что изображение F(s) некоторого неизвестного процесса f(t) равно:

Разложение на элементарные дроби.

Если корни уравнение уравнения различны, т.е. нет совпадающих, то:

где — корни уравнения; — остаточный член (не разлагается на действительные дроби);

Используя свойства линейности преобразований Лапласа, мы можем представить как сумму преобразований:

Имеем известное изображение:

— оригинал, при нулевых начальных условиях:

Разложение на элементарные дроби:

Используя метод неопределенных коэффициентов, приведем полученное выражение к общему знаменателю:

Тогда изображение разложенное на элементарные дроби принимает такой вид, что его решение можно получить из таблиц:

В заключение несколько полезных ссылок теме описанной в этой лекции:

Динамическое представление сигналов

Многие задачи радиотехники требуют специфической формы представления сигналов. Для решения этих задач необходимо располагать не только мгновенным значением сигнала, но и знать как он ведет себя во времени, знать его поведение в “прошлом” и “будущем”.

ПРИНЦИП ДИНАМИЧЕСКОГО ПРЕДСТАВЛЕНИЯ.

Данный способ получения моделей сигналов заключается в следующем. Реальный сигнал представляется суммой некоторых элементарных сигналов, возникающих в последовательные моменты времени. Теперь, если мы устремим к нулю длительность отдельных элементарных сигналов, то в пределе получим точное представление исходного сигнала. Такой способ описания сигналов называется динамическим представлением , подчеркивая тем самым развивающийся во времени характер процесса.

Широкое применение нашли два способа динамического представления.

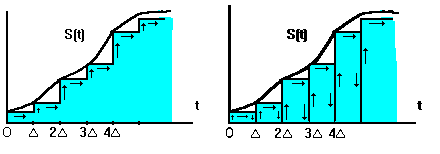
Первый способ в качестве элементарных сигналов использует ступенчатые функции, которые возникают через равные промежутки времени D (рис. 1.1). Высота каждой ступеньки равна приращению сигнала на интервале времени D.

При втором способе элементарными сигналами служат прямоугольные импульсы. Эти импульсы непосредственно примыкают друг к другу и образуют последовательность, вписанную в кривую или описанную вокруг нее (рис. 1.2).

Рассмотрим свойства элементарного сигнала, используемого для динамического представления по первому способу.

Допустим имеется сигнал, математическая модель которого выражается системой :

Такая функция описывает процесс перехода некоторого физического объекта из “нулевого” в “единичное” состояние. Переход совершается по линейному закону за время 2x. Если параметр x устремить к нулю, то в пределе переход из одного состояния в другое будет происходить мгновенно. Эта математическая модель предельного сигнала получила название функции включения или функции Хевисайда :

В общем случае функция включения может быть смещена относительно начала отсчета времени на величину t0. Запись смещенной функции такова :

ДИНАМИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ПРОИЗВОЛЬНОГО СИГНАЛА ПОСРЕДСТВОМ ФУНКЦИЙ ВКЛЮЧЕНИЯ.

Рассмотрим некоторый сигнал S(t), причем для определенности скажем, что S(t)=0 при t u — напряжение, то П = 1 В*с.

Пусть теперь величина Е стремится к нулю. Импульс, сокращаясь по длительности, сохраняет свою площадь, поэтому его высота должна неограниченно возрастать. Предел последовательности таких функций при x® 0 носит название дельта-функции , или функции Дирака :

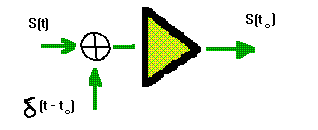
Теперь вернемся к задаче описания аналогового сигнала суммой примыкающих друг к другу прямоугольных импульсов (рис. 2) . Если S k — значение сигнала на k — ом отсчете, то элементарный импульс с номером k представляется как :

Теперь, если произвести подстановку формулы (6) в (7) предварительно разделив и умножив на величину шага D, то

Переходя к пределу при D® 0 , необходимо суммирование заменить интегрированием по формальной переменной t, дифференциал которой dt ,будет отвечать величине D . Поскольку

Итак, если непрерывную функцию умножить на дельта-функцию и произведение проинтегрировать по времени, то результат будет равен значению непрерывной функции в той точке, где сосредоточен d — импульс. Принято говорить, что в этом состоит фильтрующее свойство дельта-функции.

Обобщенные функции как математические модели сигналов.

В классической математике полагают, что функция S(t) должна принемать какие-то значения в каждой точке оси t . Однако рассмотренная функция d(t) не вписывается в эти рамки — ее значение при t = 0 не определено вообще, хотя эта функция и имеет единичный интеграл. Возникает необходимость расширить понятие функции как математической модели сигнала. Для этого в математике была введено принципиально новое понятие обобщенной функции.

В основе идеи обобщенной функции лежит простое интуитивное соображение. Когда мы держим в руках какой-нибудь предмет , то стараемся изучить его со всех сторон, как бы получить проекции этого предмета на всевозможные плоскости. Аналогом проекции исследуемой функции ¦(t) может служить, например, значение интеграла

при известной функции j(t) , которую называют пробной функцией.

Каждой функции j(t) отвечает, в свою очередь, некоторое конкретное числовое значение. Поэтому говорят, что формула (8) задает некоторый функционал на множестве пробных функций j(t). Непосредственно видно, что данный функционал линеен, то есть

Если этот функционал к тому же еще и непрерывен, то говорят, что на множестве пробных функций j(t) задана обобщенная функция ¦(t) . Следует сказать, что данную функцию надо понимать формально-аксиоматически, а не как предел соответствующих интегральных сумм.

Обобщенные фнкции , даже не заданные явными выражениями, обладают многими свойствами классических функкций. Так, обобщенные функции можно дифференцировать.

И в заключение следует сказать, что в настоящее время теория обобщенных функций получила широкое развитие и многочисленные применения. На ее основе созданы математические методы изучения процессов, для которых средства классического анализа оказываются недостаточными.

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

Энергетическое представление обобщенного динамического уравнения

Колебательная система называется линейной или нелинейной в зависимости от того, линейна или нелинейна описывающая ее система дифференциальных уравнений. Линейные системы являются частным случаем нелинейных. Однако в силу принципиальной важности линейных систем при исследовании вопросов устойчивости колебаний, а также возможности использования принципа суперпозиции решений такая классификация оправданна.

Динамические системы, моделируемые конечным числом обыкновенных дифференциальных уравнений, называют сосредоточенными или точечными системами. Они описываются с помощью конечномерного фазового пространства и характеризуются конечным числом степеней свободы. Одна и та же система в различных условиях может рассматриваться либо как сосредоточенная, либо как распределенная. Математические модели распределенных систем — это дифференциальные уравнения в частных производных, интегральные уравнения или обыкновенные уравнения с запаздывающим аргументом. Число степеней свободы распределенной системы бесконечно, и требуется бесконечное число данных для определения ее состояния.

По энергетическому признаку динамические системы делятся на консервативные и неконсервативные. Консервативные системы характеризуются неизменным во времени запасом энергии. В механике их называют гамильтоновыми. Для консервативных систем с n степенями свободы определяется гамильтониан системы H(p, q), где q_i — обобщенные координаты, p_i — обобщенные импульсы системы, i = 1, 2, . n. Гамильтониан полностью характеризует динамическую природу системы и с физической точки зрения в большинстве случаев представляет собой ее полную энергию. Эволюция во времени консервативных систем описывается уравнениями механики Гамильтона

(9)

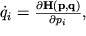
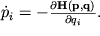
Динамические системы с изменяющимся во времени запасом энергии называются неконсервативными. Системы, в которых энергия уменьшается во времени из-за трения или рассеяния, называются диссипативными. В соответствии с этим системы, энергия которых во времени нарастает, называются системами с отрицательным трением или отрицательной диссипацией. Такие системы можно рассматривать как диссипативные при смене направления отсчета времени на противоположное.

Динамические системы называются автономными, если они не подвержены действию внешних сил, переменных во времени. Уравнения автономных систем явной зависимости от времени не содержат. Большинство реальных колебательных систем в физике, радиофизике, биологии, химии и других областях знаний неконсервативны. Среди них выделяется особый класс автоколебательных систем, которые принципиально неконсервативны и нелинейны. Автоколебательной называют динамическую систему, преобразующую энергию источника в энергию незатухающих колебаний, причем основные характеристики колебаний (амплитуда, частота, форма колебаний и т.д.) определяются параметрами системы и в определенных пределах не зависят от выбора исходного начального состояния.

Фазовые портреты типичных колебательных систем

Геометрическое представление колебаний. Метод анализа колебательных процессов с помощью исследования фазовых траекторий динамической системы был введен в теорию колебаний Л.И. Мандельштамом и А.А. Андроновым и с тех пор стал привычным при исследовании различных колебательных явлений. Обсудим несколько простых, но типичных примеров представления динамических процессов в виде траекторий изображающей точки в фазовом пространстве.

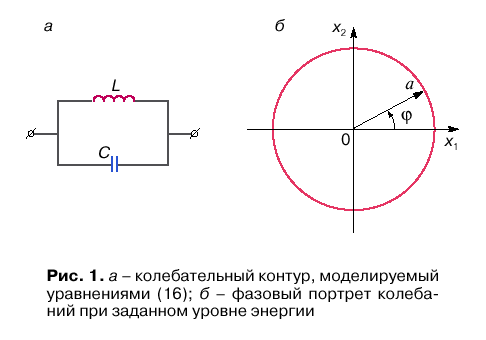
Консервативный осциллятор. Рассмотрим линейный осциллятор без потерь, уравнения которого можно сформулировать на примере колебательного LC-контура (рис. 1, а), предположив амплитуду колебаний достаточно малой. Выбрав в качестве переменной заряд q на конденсаторе, с помощью уравнений Кирхгофа получим

(10)

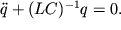
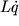
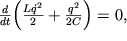
Домножив (10) на , получаем

(11)

то есть для любого момента времени выполняются равенства

(12)

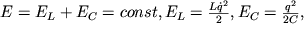
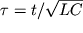
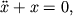
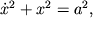
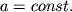
отражающие постоянство во времени полной энергии осциллятора (суммы магнитной E_L и электрической E_C энергий). В более удобных координатах уравнения консервативного осциллятора можно записать следующим образом, введя замену времени и обозначая для общности q через x :

(13)

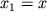
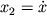
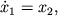
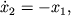
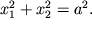
Для фазовых координат и эти уравнения преобразуются к виду

(14)

Фазовый портрет системы представляет собой окружность радиуса a с центром в начале координат. Точка в фазовом пространстве, в которой вектор фазовой скорости обращается в нуль, называется особой, и в данном случае нуль координат есть особая точка типа центр.

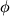
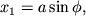
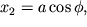
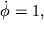
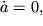
Наличие интеграла движения у рассматриваемой системы, отражающее факт сохранения энергии (12), дает возможность описать ее с помощью уравнения 1-го порядка. Действительно, определив новую переменную соотношениями

(15)

(16)

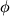
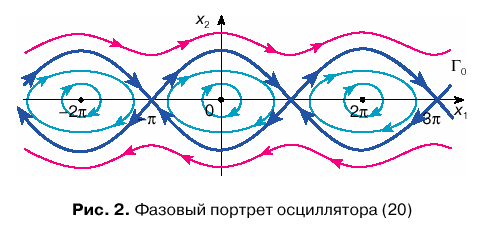
которые и представляют закон движения фазовой точки. Во времени эволюционирует одна переменная , и фазовое пространство консервативного осциллятора, таким образом, одномерно. Гармоническим колебаниям осциллятора отвечает равномерное движение изображающей точки по окружности радиуса a, как это показано на рис. 1, б.

Если консервативная система нелинейна, то ее фазовый портрет усложняется. Проиллюстрируем это на примере уравнения

(17)

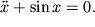
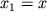
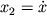
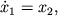
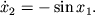
В фазовых переменных , это уравнение сводится к следующим:

(18)

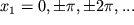
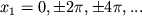
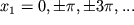
Состояния равновесия нелинейного маятника на фазовой плоскости расположены вдоль оси x₁ (x₂ = 0) в точках Соответствующий фазовый портрет системы представлен на рис. 2. Видно, что особые точки типа центр, а — неустойчивые точки типа седло.

Вблизи центров фазовый портрет соответствует линейному осциллятору: траектории представляют собой замкнутые кривые, близкие к окружностям, что отвечает по амплитуде колебаниям, близким к гармоническим. Через неустойчивые точки проходят особые интегральные кривые , называемые сепаратрисами. Они разделяют фазовое пространство на области с различным поведением. С увеличением энергии маятника его колебания от квазигармонических вблизи точек типа центр эволюционируют к нелинейным периодическим колебаниям вблизи сепаратрис. Дальнейшее увеличение энергии приведет к вращательному движению (движение вне сепаратрис). Малейшие отклонения энергии в ту или иную сторону от энергии движения по сепаратрисе приводят к качественно различным типам движения: колебательному или вращательному.

Линейный осциллятор с затуханием. Диссипация энергии, обусловленная наличием потерь, оказывает принципиальное влияние на характер движения системы. Наиболее простые закономерности проявляются в системах с полной диссипацией энергии, когда силы трения действуют по всем степеням свободы, а поступление энергии извне отсутствует. Рассмотрим процессы в линейном диссипативном осцилляторе, когда сила трения пропорциональна скорости изменения координаты. Примером такой системы служит колебательный контур, содержащий активное сопротивление R. Уравнение контура

(19)

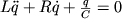
заменой переменных сводится к безразмерной форме

(20)

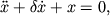
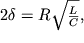
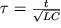
При d = 0 имеем консервативный линейный осциллятор, рассмотренный выше. Введение малого трения качественно меняет фазовый портрет системы. Для 0 1, процесс в системе апериодический:

(22)

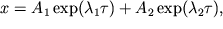
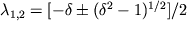
и фазовые траектории выглядят как семейство характерных кривых, по которым, как и в предыдущем случае, изображающие точки стремятся к нулю координат (рис. 3, б). Особая точка в указанных условиях является устойчивым узлом.

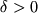
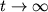
Итак, при любых значениях физических параметров системы, когда 0$» align=»middle» width=»38″ height=»27″ >, диссипативный маятник характеризуется единственным глобально устойчивым состоянием равновесия в нуле фазовых координат. Независимо от выбора начальных условий наблюдается затухающее колебательное или апериодическое движение. При любая (!) изображающая точка стремится к началу координат в устойчивый фокус либо узел.

Описанное свойство является общим для динамических систем с полной диссипацией энергии. Положения равновесия типа устойчивого фокуса или узла являются здесь глобально притягивающими в том смысле, что фазовые траектории из любой точки фазового пространства асимптотически к ним стремятся. Стационарные незатухающие колебания в линейных диссипативных системах оказываются невозможными. С физической точки зрения это понятно — нет условий поддержания колебаний. Энергия, расходуемая на преодоление сил трения, не восполняется.