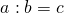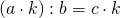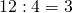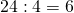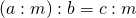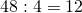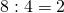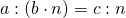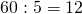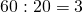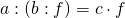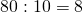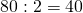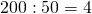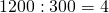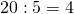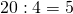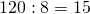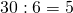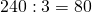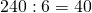Если частное больше делимого уравнение

Изменение частного с изменением делимого и делителя

Увеличение или уменьшение делимого

Если увеличить (или уменьшить) делимое в несколько раз, то частное увеличится (или уменьшится) во столько же раз.

В общем виде: если записать частное в виде равенства

то изложенное свойство частного можно записать так:

Пример. Возьмём частное двух чисел: 12 : 3 = 4 и проследим, как оно изменится при увеличении или уменьшении делимого в несколько раз. Так, если увеличить делимое, например, в 2 раза, то получится:

(12 · 2) : 3 = 24 : 3 = 8.

Новое частное оказалось больше прежнего в 2 раза. Так оно и должно быть, потому что, если 3 в 12 содержится 4 раза, то 3 в сумме 12 + 12 очевидно содержится 8 раз, т. е. в 2 раза больше, чем оно содержится в 12.

Если уменьшить делимое, например, в 2 раза, то получится:

(12 : 2) : 3 = 6 : 3 = 2.

Новое частное оказалось меньше прежнего в 2 раза, потому что, если 3 в 12 содержится 4 раза, то 3 в 6 содержится 2 раза, т. е. в 2 раза меньше, чем оно содержится в 12.

Следовательно, если увеличить или уменьшить делимое в несколько раз, то частное увеличится или уменьшится во столько же раз.

Увеличение или уменьшение делителя

Если увеличить (или уменьшить) делитель в несколько раз, то частное уменьшится (или увеличится) во столько же раз.

В общем виде: если

Пример. Возьмём частное двух чисел: 24 : 6 = 4 и проследим, как оно изменится при увеличении или уменьшении делителя в несколько раз. Так, если увеличить делитель, например, в 2 раза, то получится:

24 : (6 · 2) = 24 : 12 = 2.

Новое частное оказалось меньше прежнего в 2 раза. Так оно и должно быть, потому что 12 есть произведение 6 · 2, а чтобы разделить на произведение, можно разделить делимое на первый сомножитель (на 6) и полученное число (4) разделить затем на второй сомножитель (на 2), отчего оно уменьшится (в 2 раза).

Если уменьшить делитель, например, в 2 раза, то получится:

24 : (6 : 2) = 24 : 3 = 8.

Новое частное оказалось больше прежнего в 2 раза. Так как 6 в 24 содержится 4 раза, а 3 в два раза меньше 6, то 3, будучи меньше 6 в 2 раза, будет содержаться в 24 в 2 раза больше, т. е. 8 раз.

Следовательно, если увеличить или уменьшить делитель в несколько раз, то частное увеличится или уменьшится во столько же раз.

Предполагается, что деление совершается без остатка. Если же есть остаток, то частное может измениться иначе, чем было до этого указано.

Пример. Возьмём, например, такое деление:

23 : 5 = 4 (остаток 3),

и увеличим делимое в 3 раза. Получим:

69 : 5 = 13 (остаток 4);

по сравнению с делимым, частное увеличилось более, чем в 3 раза.

Основное свойство частного

Частное не изменится, если делимое и делитель одновременно умножить или разделить на одно и то же число.

Основное свойство частного в общем виде: если

Пример. Возьмём, например, такое деление: 60 : 15 = 4. Если увеличить делимое и делитель в 5 раз, то получим:

(60 · 5) : (15 · 5) = 300 : 75 = 4.

Частное не изменилось, потому что от увеличения делимого частное увеличивается, а от увеличения делителя оно уменьшается во столько же раз.

Если уменьшить делимое и делитель в 5 раз, то получим:

(60 : 5) : (15 : 5) = 12 : 3 = 4.

Частное не изменилось, потому что от уменьшения делимого частное уменьшается, а от уменьшения делителя оно увеличивается во столько же раз.

Как изменится частное

Как изменится частное двух чисел, если делимое увеличить (уменьшить) в несколько раз? Как изменится частное, если делитель увеличить (уменьшить) в несколько раз? Рассмотрим ответы на эти вопросы в общем случае и на конкретных примерах.

В общем виде деление двух чисел выглядит так:

Если изменить делимое или делитель, частное тоже изменится.

1) Если делимое увеличить в несколько раз, частное увеличится во столько же раз.

В общем виде: если делимое увеличить в k раз, то частное тоже увеличится в k раз:

Увеличив делимое 12 в два раза, получим 24:

Частное 6 по сравнению с первоначальным частным 3 также увеличилось в два раза.

2) Если делимое уменьшить в несколько раз, частное уменьшится во столько же раз.

В общем виде: если делимое уменьшить в m раз, то частное уменьшится в m раз:

Уменьшив делимое 48 в 6 раз, получим 8:

Частное 2 по сравнению с первоначальным частным 12 также уменьшилось в 6 раз.

3) Если делитель увеличить в несколько раз, частное уменьшится во столько же раз.

В общем виде: если делитель увеличить в n раз, то частное уменьшится в n раз:

Увеличив делитель 5 в 4 раза, получим 20:

Частное 3 по сравнению с первоначальным частным 12 уменьшилось в 4 раза.

4) Если делитель уменьшить в несколько раз, частное увеличится во столько же раз.

В общем виде: если делитель уменьшить в f раз, то частное увеличится в f раз:

Уменьшив делитель 10 в 5 раз, получим 2:

Частное 40 по сравнению с первоначальным частным 8 увеличилось в 5 раз.

А как изменится частное, если одновременно изменить и делимое, и делитель?

5) Если и делимое, и делитель увеличить или уменьшить в одинаковое число раз, то частное не изменится.

При увеличении и делимого, и делителя в 6 раз получаем:

При уменьшении и делимого, и делителя в 10 раз:

Частное 4 не изменилось.

6) Если делимое увеличить в k раз, а делимое увеличить в m раз (k>m), то частное увеличится в k:m раз.

Делимое 20 увеличим в 6 раз, делитель 4 — в 2 раза:

В итоге имеем частное 15, которое по сравнению с первоначальным частным 5 увеличилось в 6:2=3 раза.

7) Если делимое увеличить в k раз, а делитель уменьшить в m раз (k>m), то частное увеличится в km раз.

Делимое 30 увеличим в 8 раз, делитель 6 уменьшим в 2 раза:

Частное 80 по сравнению с первоначальным частным 5 увеличилось в 16раз, 16=8∙2.

8) Если делимое уменьшить в k раз, а делитель увеличить в m раз (k>m), то частное уменьшится в km раз.

Делимое 240 уменьшим в 10 раз, делитель 6 увеличим в 2 раза:

Нахождение неизвестного слагаемого, множителя: правила, примеры, решения

Чтобы научиться быстро и успешно решать уравнения, нужно начать с самых простых правил и примеров. В первую очередь надо научиться решать уравнения, слева у которых стоит разность, сумма, частное или произведение некоторых чисел с одним неизвестным, а справа другое число. Иными словами, в этих уравнениях есть одно неизвестное слагаемое и либо уменьшаемое с вычитаемым, либо делимое с делителем и т.д. Именно об уравнениях такого типа мы с вами поговорим.

Эта статья посвящена основным правилам, позволяющим найти множители, неизвестные слагаемые и др. Все теоретические положения будем сразу пояснять на конкретных примерах.

Нахождение неизвестного слагаемого

Допустим, у нас есть некоторое количество шариков в двух вазах, например, 9 . Мы знаем, что во второй вазе 4 шарика. Как найти количество во второй? Запишем эту задачу в математическом виде, обозначив число, которое нужно найти, как x. Согласно первоначальному условию, это число вместе с 4 образуют 9 , значит, можно записать уравнение 4 + x = 9 . Слева у нас получилась сумма с одним неизвестным слагаемым, справа – значение этой суммы. Как найти x ? Для этого надо использовать правило:

Для нахождения неизвестного слагаемого надо вычесть известное из суммы.

В данном случае мы придаем вычитанию смысл, который является обратным смыслу сложения. Иначе говоря, есть определенная связь между действиями сложения и вычитания, которую можно в буквенном виде выразить так: если a + b = c , то c − a = b и c − b = a , и наоборот, из выражений c − a = b и c − b = a можно вывести, что a + b = c .

Зная это правило, мы можем найти одно неизвестное слагаемое, используя известное и сумму. Какое именно слагаемое мы знаем, первое или второе, в данном случае неважно. Посмотрим, как применить данное правило на практике.

Возьмем то уравнение, что у нас получилось выше: 4 + x = 9 . Согласно правилу, нам нужно вычесть из известной суммы, равной 9 , известное слагаемое, равное 4 . Вычтем одно натуральное число из другого: 9 — 4 = 5 . Мы получили нужное нам слагаемое, равное 5 .

Обычно решения подобных уравнений записывают следующим образом:

1. Первым пишется исходное уравнение.
2. Далее мы записываем уравнение, которое получилось после того, как мы применили правило вычисления неизвестного слагаемого.
3. После этого пишем уравнение, которое получилось после всех действий с числами.

Такая форма записи нужна для того, чтобы проиллюстрировать последовательную замену исходного уравнения равносильными и отобразить процесс нахождения корня. Решение нашего простого уравнения, приведенного выше, правильно будет записать так:

4 + x = 9 , x = 9 − 4 , x = 5 .

Мы можем проверить правильность полученного ответа. Подставим то, что у нас получилось, в исходное уравнение и посмотрим, выйдет ли из него верное числовое равенство. Подставим 5 в 4 + x = 9 и получим: 4 + 5 = 9 . Равенство 9 = 9 верное, значит, неизвестное слагаемое было найдено правильно. Если бы равенство оказалось неверным, то нам следовало бы вернуться к решению и перепроверить его, поскольку это знак допущенной ошибки. Как правило, чаще всего это бывает вычислительная ошибка или применение неверного правила.

Нахождение неизвестного вычитаемого или уменьшаемого

Как мы уже упоминали в первом пункте, между процессами сложения и вычитания существует определенная связь. С ее помощью можно сформулировать правило, которое поможет найти неизвестное уменьшаемое, когда мы знаем разность и вычитаемое, или же неизвестное вычитаемое через уменьшаемое или разность. Запишем эти два правила по очереди и покажем, как применять их при решении задач.

Для нахождения неизвестного уменьшаемого надо прибавить вычитаемое к разности.

Например, у нас есть уравнение x — 6 = 10 . Неизвестно уменьшаемое. Согласно правилу, нам надо прибавить к разности 10 вычитаемое 6 , получим 16 . То есть исходное уменьшаемое равно шестнадцати. Запишем все решение целиком:

x − 6 = 10 , x = 10 + 6 , x = 16 .

Проверим получившийся результат, добавив получившееся число в исходное уравнение: 16 — 6 = 10 . Равенство 16 — 16 будет верным, значит, мы все подсчитали правильно.

Переходим к следующему правилу.

Для нахождения неизвестного вычитаемого надо вычесть разность из уменьшаемого.

Воспользуемся правилом для решения уравнения 10 — x = 8 . Мы не знаем вычитаемого, поэтому нам надо из 10 вычесть разность, т.е. 10 — 8 = 2 . Значит, искомое вычитаемое равно двум. Вот вся запись решения:

10 — x = 8 , x = 10 — 8 , x = 2 .

Сделаем проверку на правильность, подставив двойку в исходное уравнение. Получим верное равенство 10 — 2 = 8 и убедимся, что найденное нами значение будет правильным.

Перед тем, как перейти к другим правилам, отметим, что существует правило переноса любых слагаемых из одной части уравнения в другую с заменой знака на противоположный. Все приведенные выше правила ему полностью соответствуют.

Нахождение неизвестного множителя

Посмотрим на два уравнения: x · 2 = 20 и 3 · x = 12 . В обоих нам известно значение произведения и один из множителей, необходимо найти второй. Для этого нам надо воспользоваться другим правилом.

Для нахождения неизвестного множителя нужно выполнить деление произведения на известный множитель.

Данное правило базируется на смысле, который является обратным смыслу умножения. Между умножением и делением есть следующая связь: a · b = c при a и b , не равных 0 , c : a = b , c : b = c и наоборот.

Вычислим неизвестный множитель в первом уравнении, разделив известное частное 20 на известный множитель 2 . Проводим деление натуральных чисел и получаем 10 . Запишем последовательность равенств:

x · 2 = 20 x = 20 : 2 x = 10 .

Подставляем десятку в исходное равенство и получаем, что 2 · 10 = 20 . Значение неизвестного множителя было выполнено правильно.

Уточним, что в случае, если один из множителей нулевой, данное правило применять нельзя. Так, уравнение x · 0 = 11 с его помощью решить мы не можем. Эта запись не имеет смысла, поскольку для решения надо разделить 11 на 0 , а деление на нуль не определено. Подробнее о подобных случаях мы рассказали в статье, посвященной линейным уравнениям.

Когда мы применяем это правило, мы, по сути, делим обе части уравнения на другой множитель, отличный от 0 . Существует отдельное правило, согласно которому можно проводить такое деление, и оно не повлияет на корни уравнения, и то, о чем мы писали в этом пункте, с ним полностью согласовано.

Нахождение неизвестного делимого или делителя

Еще один случай, который нам нужно рассмотреть, – это нахождение неизвестного делимого, если мы знаем делитель и частное, а также нахождение делителя при известном частном и делимом. Сформулировать это правило мы можем с помощью уже упомянутой здесь связи между умножением и делением.

Для нахождения неизвестного делимого нужно умножить делитель на частное.

Посмотрим, как применяется данное правило.

Решим с его помощью уравнение x : 3 = 5 . Перемножаем между собой известное частное и известный делитель и получаем 15 , которое и будет нужным нам делимым.

Вот краткая запись всего решения:

x : 3 = 5 , x = 3 · 5 , x = 15 .

Проверка показывает, что мы все подсчитали верно, ведь при делении 15 на 3 действительно получается 5 . Верное числовое равенство – свидетельство правильного решения.

Указанное правило можно интерпретировать как умножение правой и левой части уравнения на одинаковое отличное от 0 число. Это преобразование никак не влияет на корни уравнения.

Переходим к следующему правилу.

Для нахождения неизвестного делителя нужно разделить делимое на частное.

Возьмем простой пример – уравнение 21 : x = 3 . Для его решения разделим известное делимое 21 на частное 3 и получим 7 . Это и будет искомый делитель. Теперь оформляем решение правильно:

21 : x = 3 , x = 21 : 3 , x = 7 .

Удостоверимся в верности результата, подставив семерку в исходное уравнение. 21 : 7 = 3 , так что корень уравнения был вычислен верно.

Важно отметить, что это правило применимо только для случаев, когда частное не равно нулю, ведь в противном случае нам опять же придется делить на 0 . Если же частным будет нуль, возможны два варианта. Если делимое также равно нулю и уравнение выглядит как 0 : x = 0 , то значение переменной будет любым, то есть данное уравнение имеет бесконечное число корней. А вот уравнение с частным, равным 0 , с делимым, отличным от 0 , решений иметь не будет, поскольку таких значений делителя не существует. Примером может быть уравнение 5 : x = 0 , которое не имеет ни одного корня.

Последовательное применение правил

Зачастую на практике встречаются более сложные задачи, в которых правила нахождения слагаемых, уменьшаемых, вычитаемых, множителей, делимых и частных нужно применять последовательно. Приведем пример.

У нас есть уравнение вида 3 · x + 1 = 7 . Вычисляем неизвестное слагаемое 3 · x , отняв от 7 единицу. Получим в итоге 3 · x = 7 − 1 , потом 3 · x = 6 . Это уравнение решить очень просто: делим 6 на 3 и получаем корень исходного уравнения.

Вот краткая запись решения еще одного уравнения ( 2 · x − 7 ) : 3 − 5 = 2 :

( 2 · x − 7 ) : 3 − 5 = 2 , ( 2 · x − 7 ) : 3 = 2 + 5 , ( 2 · x − 7 ) : 3 = 7 , 2 · x − 7 = 7 · 3 , 2 · x − 7 = 21 , 2 · x = 21 + 7 , 2 · x = 28 , x = 28 : 2 , x = 14 .